Resoluções – Cinemática
RESOLUÇÕES
CINEMÁTICA
(2015, 2016 e 2017)
MOVIMENTO UNIFORME
01– Esse exercício é de apenas velocidade média, só precisamos tomar cuidado com as transformações:


02- Considere: 1 nó = 1 milha marítima/hora.
Como um nó equivale à 1 milha marítima/hora, a embarcação com velocidade de 10 nós, se movimenta em uma hora o equivalente à 10 milhas. O mesmo raciocínio para a de 30 nós, só que nesse caso são 30 milhas.
Bom, se analisarmos que ambas estão em direções opostas, a suavelocidade relativa deve ser somada, já que uma se move 10 milhas e a outra 30 para o mesmo ponto, o de encontro.
Sendo assim:
Velocidade relativa das embarcações = 10 + 30 = 40 milhas/hora
Jogando na fórmula da velocidade:
![]()
![]()
Isolando o tempo:
![]()
![]()
R- D
03-
R- A
04-
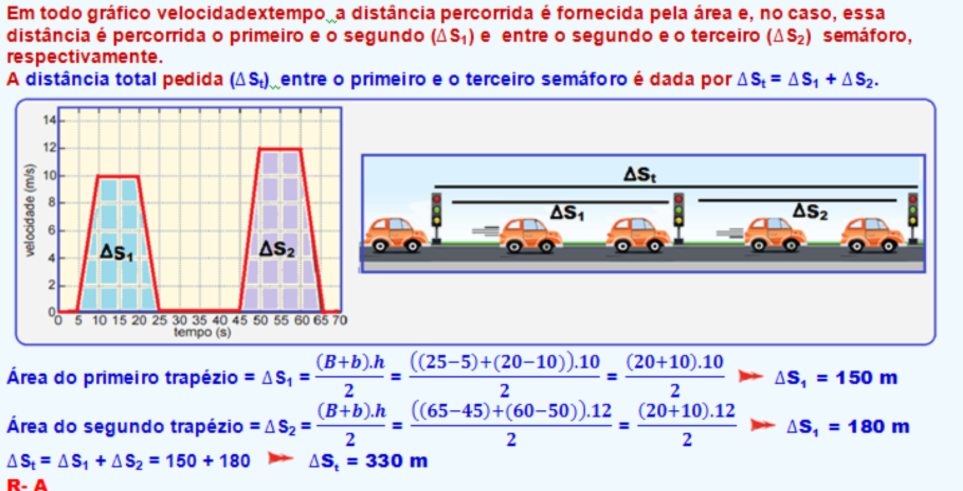
![]() S1 +
S1 + ![]() S2 = 150 + 180
S2 = 150 + 180 ![]()
![]() St = 330 m
St = 330 m
R- A
05-
Vamos chamar de d a primeira metade do trajeto, tal que:
![]() Quando percorrida com V1 = 25 m/s demora um intervalo de tempo ∆t1 tal que V1 = d/∆t1
Quando percorrida com V1 = 25 m/s demora um intervalo de tempo ∆t1 tal que V1 = d/∆t1 ![]() 25 = d/∆t1
25 = d/∆t1 ![]() ∆t1 =
∆t1 = ![]() (I)
(I)
![]() Quando percorrida com V2 = 15 m/s demora um intervalo de tempo ∆t2 = ∆t1 + 7200 tal que V2 = d/∆t2
Quando percorrida com V2 = 15 m/s demora um intervalo de tempo ∆t2 = ∆t1 + 7200 tal que V2 = d/∆t2 ![]() 15 = d/(∆t1 + 7200) (II).
15 = d/(∆t1 + 7200) (II).
(I) em (II) ![]() 15 = d/(
15 = d/(![]() + 7200)
+ 7200) ![]() 15.
15.![]() + 15.7200 = d
+ 15.7200 = d ![]() 0,6d – d = – 108000
0,6d – d = – 108000 ![]() 0,4d = 108000
0,4d = 108000 ![]() d = 270 000 m = 270 km (III).
d = 270 000 m = 270 km (III).
(III) em (I) ![]() ∆t1 =
∆t1 = ![]() = 10800 s
= 10800 s ![]() ∆t1 =
∆t1 = ![]() = 3 h
= 3 h ![]() ∆t2 = 3 + 2
∆t2 = 3 + 2 ![]() ∆t2 = 5 h (tempo gasto na primeira metade do trajeto com velocidade de 15 m/s).
∆t2 = 5 h (tempo gasto na primeira metade do trajeto com velocidade de 15 m/s).
Como a primeira metade do trajeto tem 270 km, a segunda metade terátambém 270 km e a distância
entre as duas cidades será de D = 270×2 = 540 km.
Como, pelo enunciado, a segunda metade V2 desse trajeto é sempre percorrida com velocidade constante e igual à média aritmética das duas velocidades anteriores ![]() V2 =
V2 = ![]() = 20 m/sx3,6 = 72 km/h.
= 20 m/sx3,6 = 72 km/h.
Tempo ∆t3 decorrido para percorrer a segunda metade do percurso de d = 270 km com V2 = 72 km/h
72 = 270/∆t3 ![]() ∆t3 =
∆t3 = ![]() = 3,75 h
= 3,75 h
A velocidade média (Vm) ao longo de todo o trajeto é fornecida por ![]() Vm=
Vm= ![]() =
= ![]() =
= ![]()
![]() Vm = 80 km/h
Vm = 80 km/h
R- C
06-
Ultrapassagem
Trem de comprimento (x = 150 m) atravessando totalmente um túnel de comprimento (c=?) ![]() observe que para atravessar completamente o túnel, um ponto P fixo em qualquer parte do trem
observe que para atravessar completamente o túnel, um ponto P fixo em qualquer parte do trem
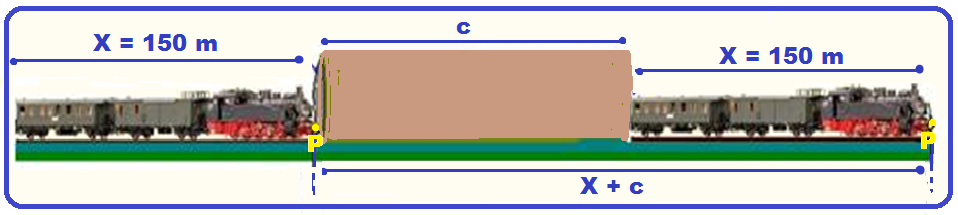
deve percorrer uma distância ΔS = 150 + c, com velocidade V num intervalo de tempo Δt, tal que ![]()
V = ![]()
![]() 16 =
16 = ![]()
![]() 150 + c = 800
150 + c = 800 ![]() c = 800 – 150
c = 800 – 150 ![]() c = 650 m
c = 650 m
R- B
07- VP = ![]()
![]() 8 =
8 = ![]()
![]() t’ =
t’ = ![]()
![]() t’ = 150 s
t’ = 150 s
VS = ![]()
![]() 5 =
5 = ![]()
![]() t’’ =
t’’ = ![]()
![]() t’’ = 240 s
t’’ = 240 s
∆t = 240 – 150 ![]() ∆t = 90 s
∆t = 90 s
08-Intervalo de tempo (∆t’) que demorou para percorrer a distância entre 0 km e 5 km com V’ = 60 km/h ![]() V’ =
V’ = ![]()
![]() 60 =
60 = ![]()
![]() ∆t’ =
∆t’ = ![]()
![]() ∆t’ =
∆t’ =![]() h.
h.
Intervalo de tempo (∆t’’) que demorou para percorrer a distância entre 5 km e 10 km com V’’ = 30 km/h ![]() V’’ =
V’’ = ![]()
![]() 30 =
30 = ![]()
![]() ∆t’’ =
∆t’’ = ![]()
![]() ∆t’ =
∆t’ = ![]() h.
h.
Velocidade média total ![]() Vm =
Vm = ![]() =
= 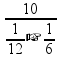 =
= ![]()
![]() Vm =
Vm = ![]()
![]() Vm = 40 km/h
Vm = 40 km/h
R- C
09- Para esse exercício podemos dar a resposta logo de cara, ou realizar contas, vamos fazer ambos:
Se analisarmos a descrição, a velocidade de um é a metade da outra, portanto ele irá percorrer metade da distância também, sendo assim, percorrerá ![]() do caminho total, enquanto o outro carro percorrerá
do caminho total, enquanto o outro carro percorrerá ![]() .
.


10-– Velocidade do atleta 1 que partiu antes e percorreu ∆S1 = 42 km em ∆t1 = 2 h ![]() V1 =
V1 = 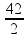
![]()
V1 = 21 km/h.
No instante em que o atleta 2 partiu, o atleta 1 já havia percorrido, em 0,5 h a distância ∆S com velocidade de V1 = 21 km/h, tal que ![]() V1 =
V1 = 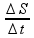
![]() 21 =
21 = 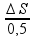
![]() ∆S = 10,5 km.
∆S = 10,5 km.
Para que eles cheguem juntos no final dos 42 km o atleta 2 deverá percorrer essa distância ∆S2 = 42 km em ∆t2 = 2,0 – 0,5 = 1,5 h com velocidade V2 tal que ![]() V2 =
V2 = 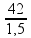 = 28 km/h.
= 28 km/h.
Assim, para que eles terminem a prova empatados o atleta 1 deverá ter velocidade de V = 28 – 21 = 7 km/h a mais que a do atleta 2.
R- D
11-Para analisar esse exercício precisamos primeiro entender que no final da corrida trem e homem estarão lado a lado, na mesma posição, ou seja, a posição final de ambos é igual. Sabendo disso e que ambos estão em velocidade constante:


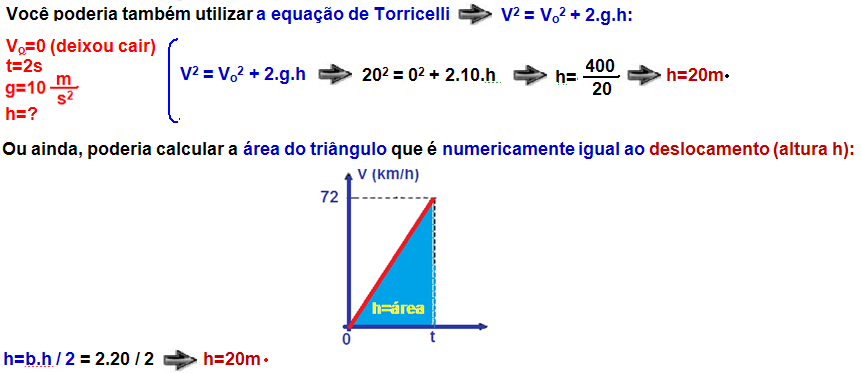
12- Em todo gráfico VXt a área entre a reta representativa e o eixo dos tempos é numericamente
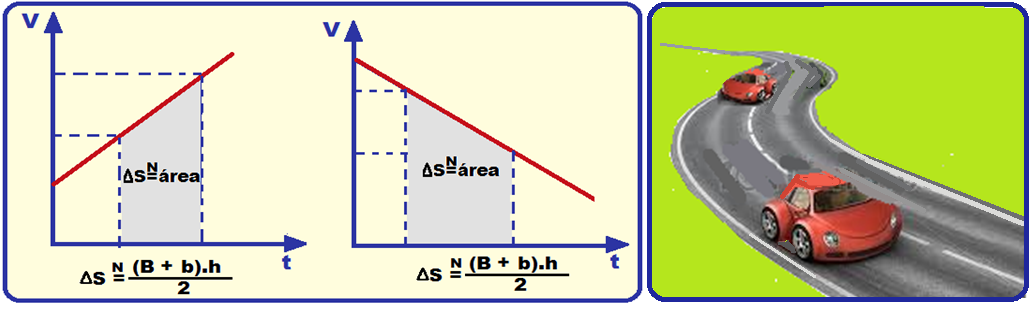
igual à variação de espaço ΔS, entre dois instantes quaisquer t1 e t2.
Os corpos A e B voltam a se encontrar quando as áreas entre as curvas características da velocidade
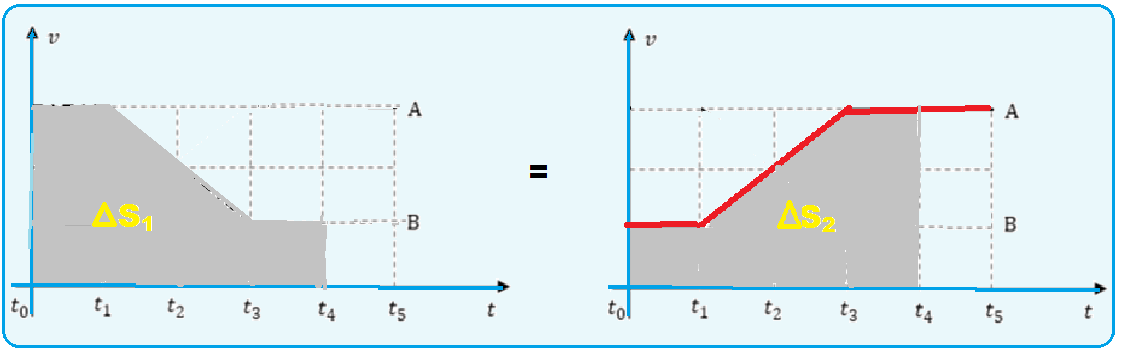
(v) e o tempo (t) forem iguais. Analisando o gráfico as áreas são iguais no instante t4.
R- A
13-


14-

15-
Veja a figura abaixo:
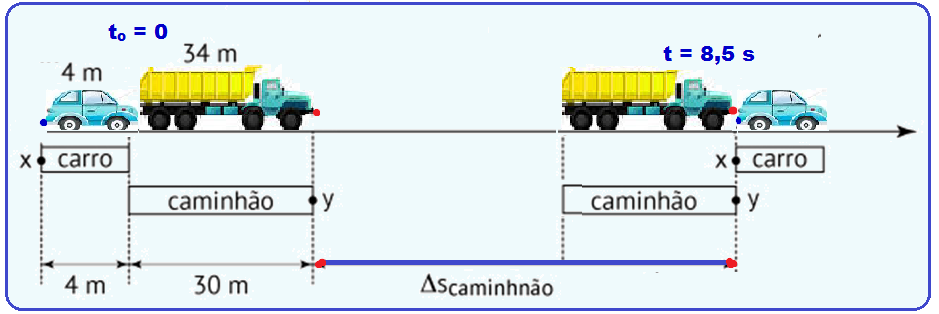

R- D
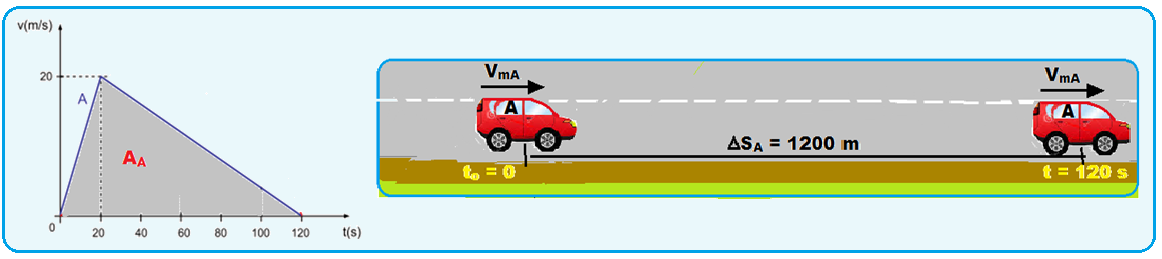
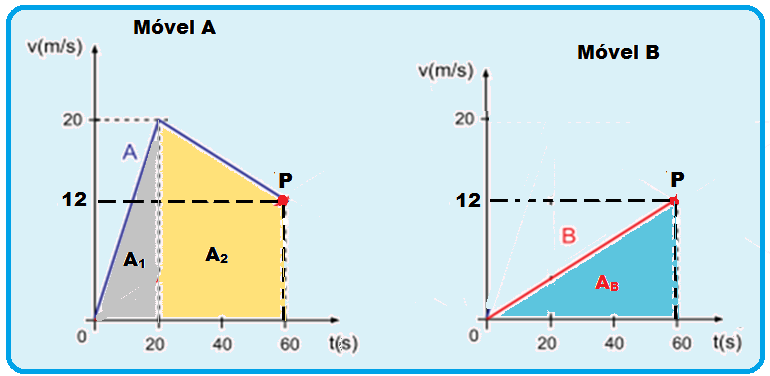
16-a) o módulo das velocidades escalares médias de A e de B, em m/s, durante os 120 s.
Em todo gráfico da velocidade escalar em função do tempo, a área A entre a reta representativa (linha cheia) e o eixo dos tempos é numericamente igual ao deslocamento ∆S efetuado pelo móvel em determinado intervalo de tempo ∆t.
Calculando o deslocamento do móvel A entre to = 0 e t = 120 s pela área AA:
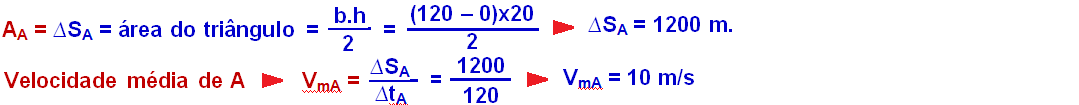
Calculando o deslocamento do móvel B entre to = 0 e t = 120 s pela área AB:
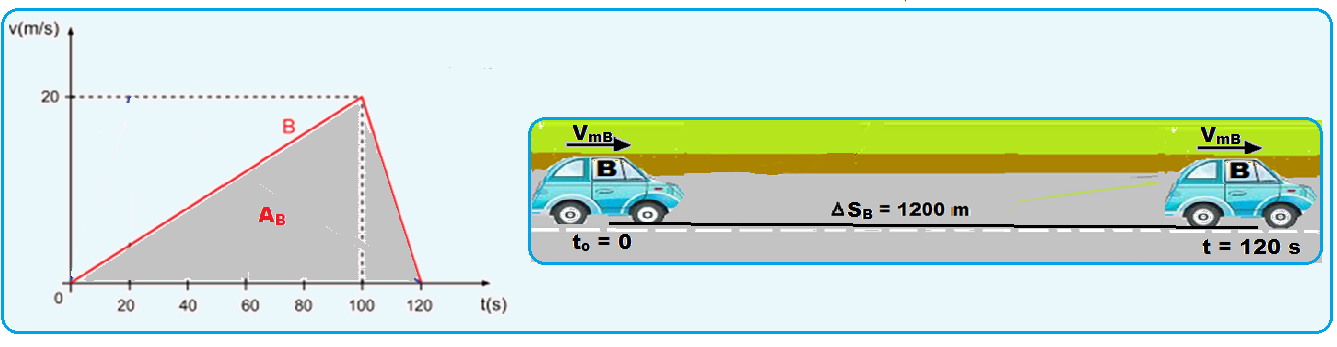

b) a distância entre os veículos, em metros, no instante t = 60 s.
Observe que, no instante t = 60 s eles possuem a mesma velocidade, que é o ponto (P) onde as retas

Acontece que no instante t = 60s, VB = VA = V’ = 12 m/s.
Deslocamentos de A e de B entre 0 e 60 s pela área:
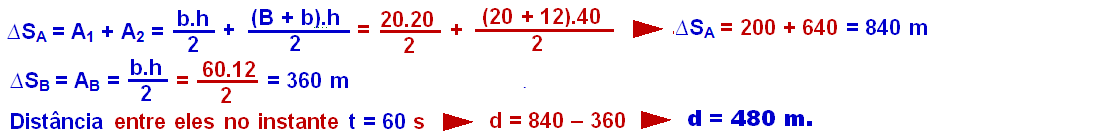
MOVIMENTO UNIFORMEMENTE VARIADO
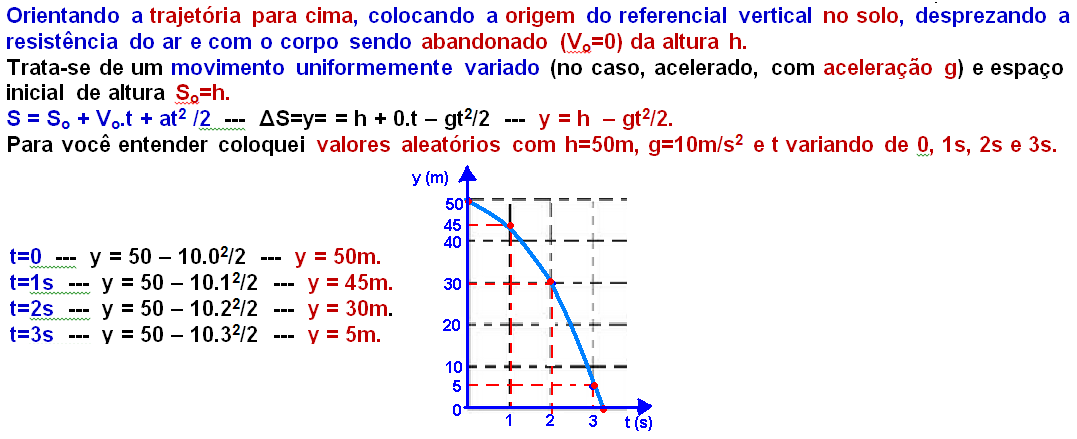
01- Durante a primeira etapa entre a detecção do problema pelo motorista e o acionamento do freio, a velocidade do veículo permanece constante com ele em movimento uniforme (MU) e o gráfico é uma reta horizontal paralela ao eixo da distância.
Durante a segunda etapa, após o acionamento do freio, o veículo sofre desaceleração constante, e realiza um movimento uniformemente variado(retardado, pois está freando).
Como a velocidade V está variando em função da distância d a equação utilizada é a equação de Torricelli (V2 = Vo2+ 2.(-a).d, sendo a aceleração negativa pois está freando) e, assim, você pode concluir que o gráfico da velocidade em função da distância é um arco de parábola com a intensidade da velocidade diminuindo.
R- E
02-

03-
As alternativas (A) e (B) estão erradas, pois o gráfico Sxt fornece apenas a posição do móvel em cada instante, independente da trajetória do mesmo.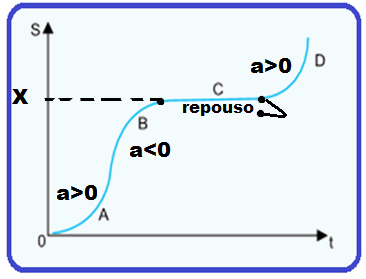
Pelo enunciado o trecho C não é arco de parábola (reta) o que significa quenesse trecho o móvel está em repouso numa posição qualquer, por exemplo X.
Nos trechos A, B e D o movimento é um MUV de equação S = So + Vot + ![]() onde a é a aceleração que épositiva com a concavidade da parábola para cima e negativa com a concavidade para baixo.
onde a é a aceleração que épositiva com a concavidade da parábola para cima e negativa com a concavidade para baixo.
R- D
04-
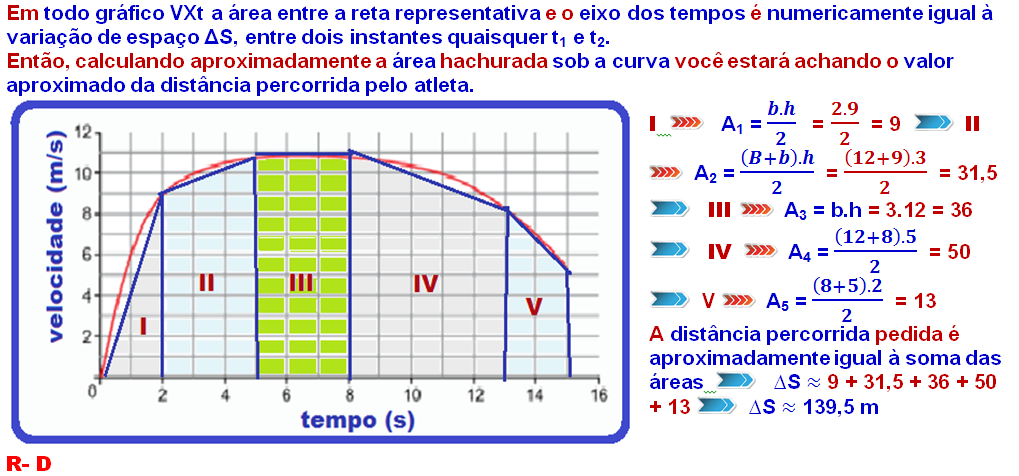
05-
Errado ![]() em t > 0 a trajetória é uma exponencial.
em t > 0 a trajetória é uma exponencial.
b) Errado ![]() em t = 0 o objeto está a 10 m de distância do observador.
em t = 0 o objeto está a 10 m de distância do observador.
c) Correto ![]() O movimento é dado pela função x(t) = -10 + 4t +2t2, dessa forma, o termo quadrático constante caracteriza um movimento retilíneouniformemente variado.
O movimento é dado pela função x(t) = -10 + 4t +2t2, dessa forma, o termo quadrático constante caracteriza um movimento retilíneouniformemente variado.
d) Errado ![]() em t = 0 a velocidade igual a velocidade inicial do objeto, que vale 4 m/s.
em t = 0 a velocidade igual a velocidade inicial do objeto, que vale 4 m/s.
e) Errado ![]() quando t = 2 s o objeto está a 6 m do observador
quando t = 2 s o objeto está a 6 m do observador ![]()
![]()
![]()
R- Portanto, a resposta correta é a alternativa C.
06-
Função (equação) horária da velocidade do MUV
O móvel da figura abaixo tem velocidade Vo no instante to e velocidade V num instante posterior t.

Admitindo to = 0 como a origem dos tempos ![]() a = (V – Vo)/(t – to)
a = (V – Vo)/(t – to) ![]() a = (V – Vo)/t
a = (V – Vo)/t ![]() V – Vo = a.t
V – Vo = a.t ![]()
V = Vo + a.t, sendo a a aceleração do móvel.

Como Vo = 0 ![]() V = a.t.
V = a.t.
R- A
07-Correta ![]() A crosta terrestre é formada por vários blocos rochosos,denominados placas litosféricas ou placas tectônicas.
A crosta terrestre é formada por vários blocos rochosos,denominados placas litosféricas ou placas tectônicas.
Esses blocos estão em constante movimento, podendo se afastar uns dos outros, caracterizando uma zona de divergência ou se aproximar, formando uma zona de convergência.
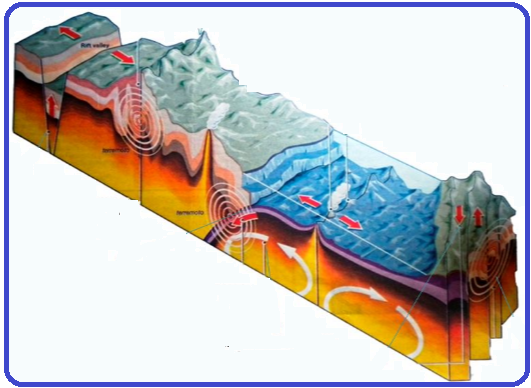
Nas zonas de convergência pode ocorrer a colisão ou a subducção de placas, o que produz um acúmulo de pressão e descarga de energia, que se propaga em forma de ondas sísmicas, caracterizando o terremoto.
08) Correta ![]() Na figura abaixo podemos visualizar a divisão das placas tectônicas, entre as quais,
Na figura abaixo podemos visualizar a divisão das placas tectônicas, entre as quais,
01) Errada ![]() S(t) = -t + 15
S(t) = -t + 15 ![]() para qualquer t S(t) < 0 (retrógrado).
para qualquer t S(t) < 0 (retrógrado).
02) Errada ![]() S(t) não é injetora (a 0), portanto, também não é bijetora (bijetora = injetora + sobrejetora)
S(t) não é injetora (a 0), portanto, também não é bijetora (bijetora = injetora + sobrejetora)
04) Correta ![]() S(t) = t2+2t+3
S(t) = t2+2t+3 ![]() S(2) = 22+2.2+3 = 11
S(2) = 22+2.2+3 = 11 ![]() S(6) = 62+2.6+3 = 51
S(6) = 62+2.6+3 = 51 ![]() VM = ∆S/∆t
VM = ∆S/∆t ![]() VM=(51-11)/(6-2) = 40/4
VM=(51-11)/(6-2) = 40/4 ![]() VM= 10 m/s.
VM= 10 m/s.
08) Errada ![]() at2 – bt + c (MUV), só será UM se a 0.
at2 – bt + c (MUV), só será UM se a 0.
16) Correta ![]() S(0) = c = 3
S(0) = c = 3 ![]() S(1) = a + b + c = 5
S(1) = a + b + c = 5 ![]() S(2) = 4ª + 2b+c = 7
S(2) = 4ª + 2b+c = 7 ![]() a + b = 2, 4a + 2b = 4, 2a + b = 2
a + b = 2, 4a + 2b = 4, 2a + b = 2 ![]() 2a +(2-a) = 2
2a +(2-a) = 2 ![]() a=0, b=2
a=0, b=2 ![]() S(t) = 2t + 3.
S(t) = 2t + 3.
R- 04 e 16.
08- Observando o enunciado percebemos que o trem realiza um Movimento Uniformemente Variado (MUV) com aceleração máxima a = 0,09g = 0,09×10 = 0,9 m/s2 e que não foi fornecido nenhuma informação detempo para determinarmos a distância mínima ( ∆S) percorrida.

MOVIMENTOS VERTICAIS
01-Observe que, pelo enunciado, é pedida a velocidade do parafuso em relação ao chão do elevador e, antes de se desprender do teto (instante to), o parafuso encontra-se em repouso em relação ao chão do elevador, pois a distância entre eles não está variando.
Assim, as alternativas a, b e c não satisfazem.
Após desprender-se do teto (instante to) o parafuso efetua uma queda livre em relação ao chão do elevador com a velocidade variando com o tempo conforme a equação V = Vo + gt = 0 + gt ![]()
V = gt (o sinal de gt depende da orientação da trajetória).
Como o enunciado pede o módulo da velocidade você terá ΙVΙ = gt e, essa função é do primeiro grau representada por uma reta inclinada.
R- E
02-Como a bola sai da mesa com velocidade inicial (horizontal Vo) e caisujeita à aceleração da gravidade g, trata-se de um lançamento horizontal.
Olhando de cima você está vendo o movimento horizontal da bola eolhando de frente, o movimento vertical da mesma.
Veja como a situação apresentada pode ser esquematizada (lançamento horizontal) com as seguintes características:
Colocando-se a origem do sistema de referência no ponto de lançamento, orienta-se, por exemplo, o eixo X para a direita e o eixo Y para baixo.
Decompõe-se o movimento em duas parcelas:
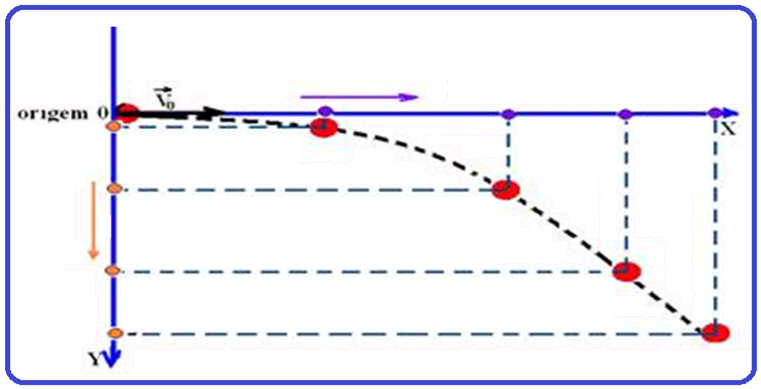
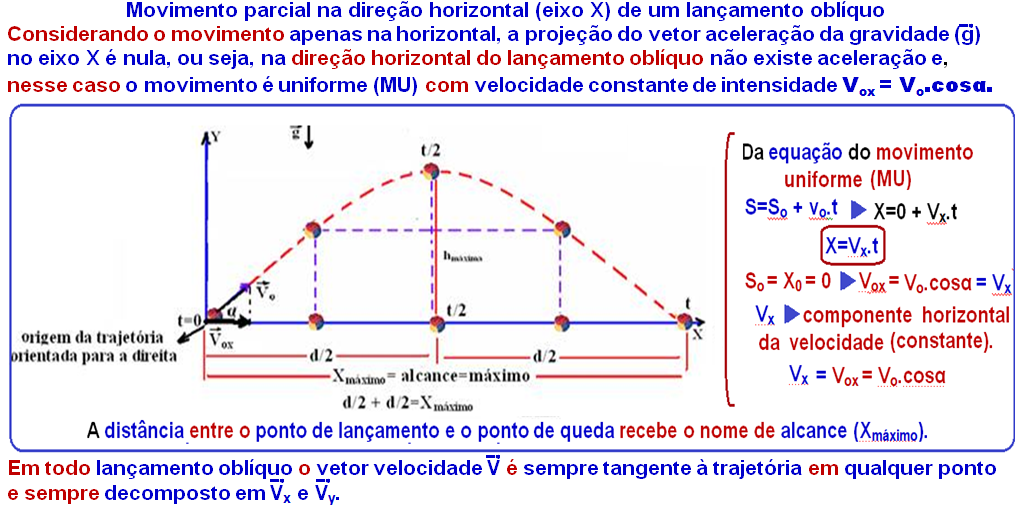
![]() Segundo o eixo X
Segundo o eixo X ![]() trata-se de um movimento horizontal uniforme comvelocidade constante de intensidade Vo , que é a velocidade de lançamento
trata-se de um movimento horizontal uniforme comvelocidade constante de intensidade Vo , que é a velocidade de lançamento ![]() S = So + V.t
S = So + V.t ![]() X = 0 + Vo.t
X = 0 + Vo.t ![]() X = Vo.t
X = Vo.t
![]() Segundo o eixo Y
Segundo o eixo Y ![]() trata-se de um movimento uniformemente variadocom velocidade inicial
trata-se de um movimento uniformemente variadocom velocidade inicial
Vo = 0, ou seja, é uma queda livre com o corpo abandonado da origem, sujeito apenas à aceleração da gravidade, de intensidade g, direção vertical e sentido para baixo.
Equações:
S = So + Vo.t + at2/2 ![]() Y = 0 + 0.t + gt2/2
Y = 0 + 0.t + gt2/2 ![]() Y = g.t2/2
Y = g.t2/2
Vy = Voy + a.t ![]() Vy= 0 + g.t
Vy= 0 + g.t ![]() Vy = g.t
Vy = g.t
V2 = Vo2 + 2.a.ΔS ![]() Vy2 = Voy2 + 2.g.Δh
Vy2 = Voy2 + 2.g.Δh ![]() Vy2 = 02 + 2.g.Δh
Vy2 = 02 + 2.g.Δh ![]() Vy2 = 2.g.Δh
Vy2 = 2.g.Δh
No caso do exercício:
Cálculo do tempo t que a bola demora para atingir o solo onde y = 1,25 m ![]() Y = g.t2/2
Y = g.t2/2 ![]() 1,25 =
1,25 =
![]()
![]() t =
t = ![]()
![]() t = 0,5 s.
t = 0,5 s.
Esse tempo de queda na vertical é o mesmo que a bola demora para percorrer X = 2,4 m na horizontal com velocidade Vo ![]() X = Vo.t
X = Vo.t ![]() 2,4 = Vo.0,5
2,4 = Vo.0,5 ![]() Vo = 4,8 m/s.
Vo = 4,8 m/s.
R- D
03-

04- Corpos abandonados com Vo = 0 ou lançados verticalmente para baixo com Vo ≠ 0 de um mesmo local e da mesma altura (desprezando-se os efeitos do ar)demoram o mesmo tempo para chegar ao solo, independente de suas massas.
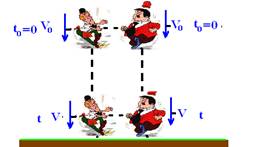
A velocidade com que eles chegam ao solo também é a mesma.
R- A
05-

R- C
06-
R- E
LANÇAMENTO OBLÍQUO
01-

02- Para calcularmos a altura máxima precisaremos decompor esse exercício em x e y, para obtermos todas as informações possíveis de y, inicialmente decompondo a velocidade V0 em V0x e V0y:
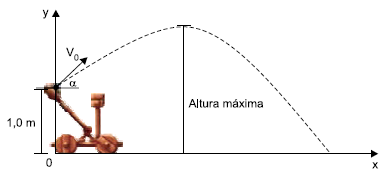
![]()
![]()
A seta vermelha representa nosso V0y e a azul nosso V0x. Como fornecido no exercício o ângulo entre x e V0 é de 30°, o mesmo para x e V0x. Vamos calcular V0y:

![]()
![]()
Passando V0y para o lado direito, podemos observar que ele é o cateto oposto de ![]() , sendo assim:
, sendo assim:
![]()
![]()
Substituindo os valores:
![]()
Multiplicando em cruz:
![]()
Isolando V0y:
![]()
Sabendo disso, podemos calcular a altura por Torricelli:
![]()
Onde: Vfy é a velocidade final em y
V0y é a velocidade inicial em y
![]() é o deslocamento em y
é o deslocamento em y
a é a aceleração em y
Vamos substituir os valores:
A altura máxima equivale ao ponto aonde a velocidade é 0, portanto nosso Vfy deve ser 0.
O ![]() , portanto, será nossa altura.
, portanto, será nossa altura.
A aceleração deve ser negativa, pois o movimento está subindo e a gravidade exerce uma força contrária, para baixo.
![]()
Passando o h para o outro lado:
![]()
Calculando o h:
![]()
Não podemos esquecer que a catapulta já estava na altura de 1m, portanto h = 20 + 1 = 21m.
R- E
03-
d) Errada ![]() Podemos calcular o tempo em que o objeto atinge o ponto mais alto e chega ao solo novamente, através da equação dada no enunciado:
Podemos calcular o tempo em que o objeto atinge o ponto mais alto e chega ao solo novamente, através da equação dada no enunciado:
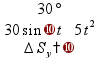
![]()
![]()
![]()
Resolvendo essa equação de segundo grau encontramos que o tempo de subida é de 1,5 segundos. Como o tempo de descida é igual ao tempo de subida, o tempo total é 3 segundos.
e) Correto ![]() Podemos calcular a distância horizontal através da equação em x, dada no enunciado, utilizando o tempo calculado no item d, já que é o mesmo.
Podemos calcular a distância horizontal através da equação em x, dada no enunciado, utilizando o tempo calculado no item d, já que é o mesmo.
![]()
![]()
![]()
R- Portanto, a resposta correta é a alternativa E.
04- Observe que são desprezados os atritos e o helicóptero está em movimento retilíneo e, como cada pacote atinge o solo em um ponto exatamente embaixo do helicóptero, ele (helicóptero) está com velocidade constante (aceleração nula).
R- C
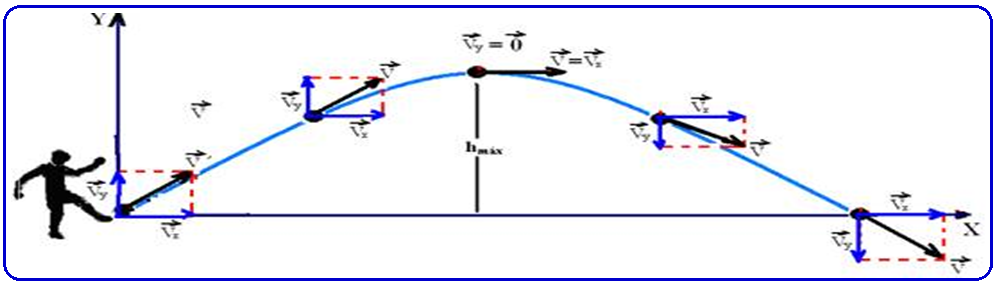
05- Trata-se de um lançamento oblíquo onde,na vertical (Y) você tem as funções(equações), com os respectivos gráficos
Equação da posição (dos espaços) ou da altura Y
S=So + Vo.t + a.t2/2 — Y=Yo + Voy.t – gt2/2 — Y=0 + Voy.t – gt2/2 — Y= Voy.t – gt2/2, com Voy=Vo.senα
![]()
Equação da velocidade Vy
V=Vo + a.t — Vy=Voy – g.t, com Voy=Vo.senα
![]()
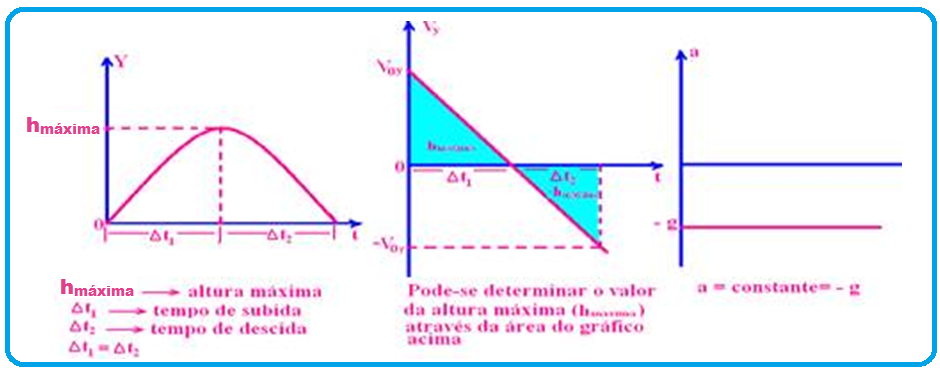
Movimento parcial na direção horizontal (eixo X)
Sendo o movimento apenas na horizontal, a projeção do vetor aceleração da gravidade (![]() ) no eixo X é nula e, nesse caso o movimento é uniforme (MU) com velocidade constante Vox, de equação X = Voxt e cujo gráfico da velocidade Vx , constante, é uma reta paralela ao eixo dos tempos:
) no eixo X é nula e, nesse caso o movimento é uniforme (MU) com velocidade constante Vox, de equação X = Voxt e cujo gráfico da velocidade Vx , constante, é uma reta paralela ao eixo dos tempos:
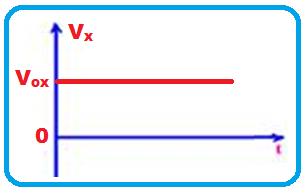
R- B
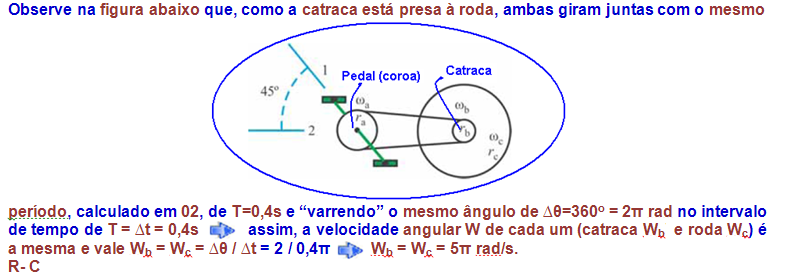
MOVIMENTO CIRCULAR
01-A seguir, um breve resumo teórico:
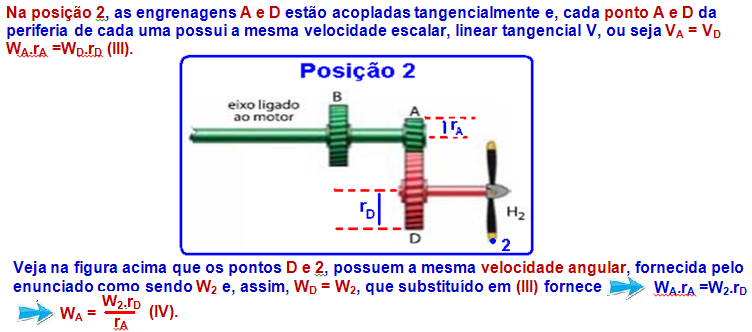
Acoplamento de polias e engrenagens

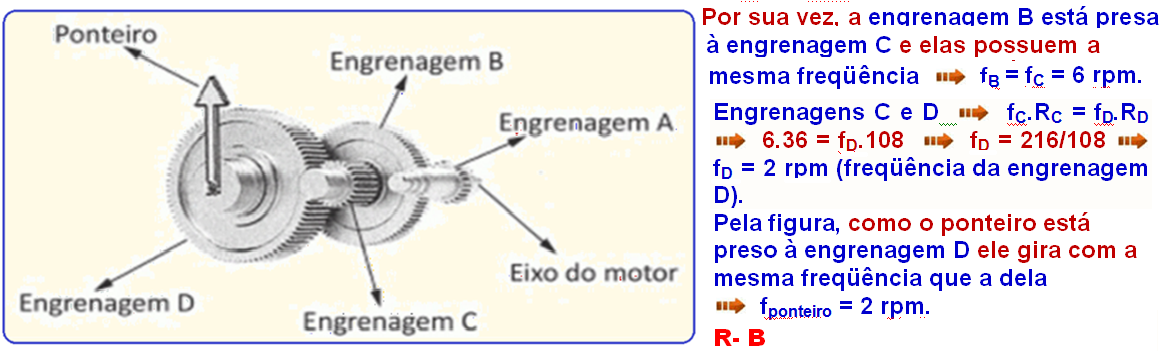
Como todos os dentes de cada engrenagem se encaixam perfeitamente, os raios das mesmas são diretamente proporcionais ao número de dentes![]() RA= 24; RB = 72; RC= 36 e RD = 108.
RA= 24; RB = 72; RC= 36 e RD = 108.
Observe nafigura que a engrenagem A está presa ao motor de freqüência 18 rpm, então fA = 18 rpm.
Engrenagens A e B![]() fA.RA = fB.RB
fA.RA = fB.RB![]() 18.24 = fB.72
18.24 = fB.72 ![]() fB = 432/72
fB = 432/72 ![]() fB = 6 rpm (freqüência da engrenagem B).
fB = 6 rpm (freqüência da engrenagem B).
02 – Para resolver esse exercício primeiramente precisamos passar as unidades para segundos, como está em minutos, então vamos dividir por 60:
![]()
No caso hertz representa rotações por segundo.
Bom como cada rotação equivale à 2π, afinal temos um círculo:
![]()
Agora que temos ambas as velocidades angulares, precisamos apenas subtrair uma da outra para calcularmos a variação:
![]()
R – B
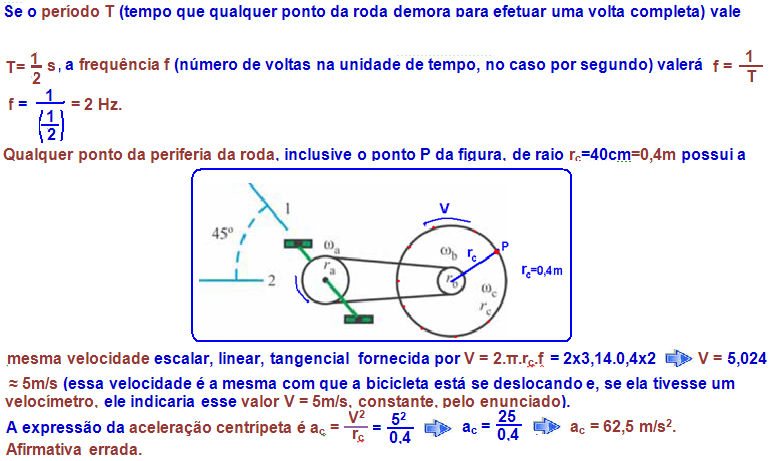
03- a) Se a freqüência da hélice é de f = 4 Hz, o período vale T = ![]() =
= ![]()
![]() T = 0,25 s (tempo que demora para efetuar uma volta completa).
T = 0,25 s (tempo que demora para efetuar uma volta completa).
Se, para efetuar uma volta completa a hélice demora T = 0,25 s, para efetuar 12 voltas completas ela demorará ![]() = 12×0,25 = 3 s.
= 12×0,25 = 3 s.
Como o avião se desloca ![]() com velocidade escalar constante V = 2 m/s em
com velocidade escalar constante V = 2 m/s em ![]() = 3 s
= 3 s ![]() V =
V = ![]()
![]()
2 = ![]()
![]() ∆S = 6 m.
∆S = 6 m.
b)
Velocidade angular (W) de um MCU
Considere um móvel em MCU de modo que no instante to sua posição seja determinada pelo ângulo de fase φo e num outro instante t (t > to) pelo ângulo de fase φ.
Assim, observa-se que, no intervalo de tempo Δt = t – to, o raio que acompanha o móvel em seu movimento descreveu “varreu” um ângulo Δφ = φ – φo.
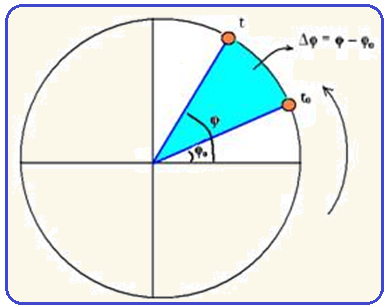


Cálculo da velocidade V’ de rotação de um ponto da extremidade R = 1m de uma das pás da hélice ![]() W =
W = ![]()
![]() 24 =
24 = ![]()
![]() V’ = 24 m/s
V’ = 24 m/s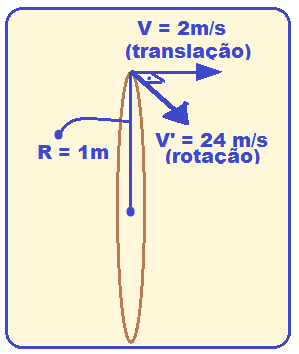
Acontece que a velocidade vetorial, em relação ao solo, é a soma vetorial da velocidade devida à rotação na extremidade da hélice (V’ = 24 m/s) com a velocidade de translação do avião (V = 2 m/s), pois ambas são perpendiculares.
VR2 = V2 + V’2 = 22 + 242 = 4 + 576 = 580 ![]() VR=
VR= ![]()
![]() VR
VR ![]() 24,1 m/s.
24,1 m/s.
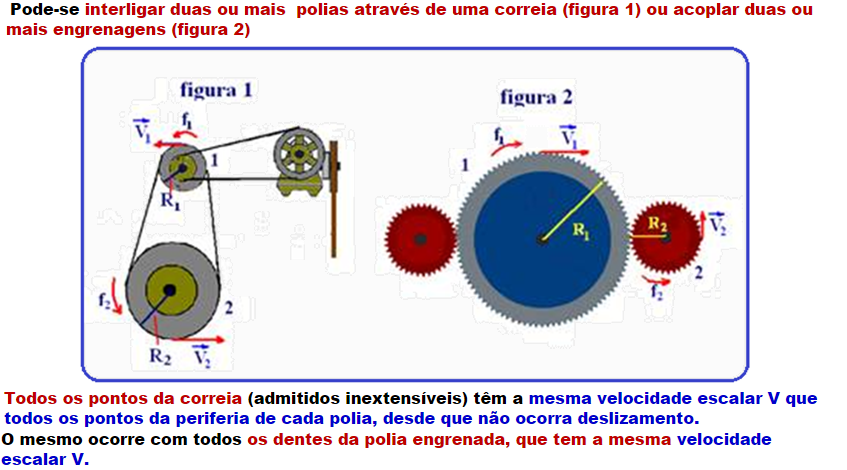
04-Pode-se interligar duas ou mais polias através de uma correia (figura 1) ou acoplar duas ou mais engrenagens (figura 2)
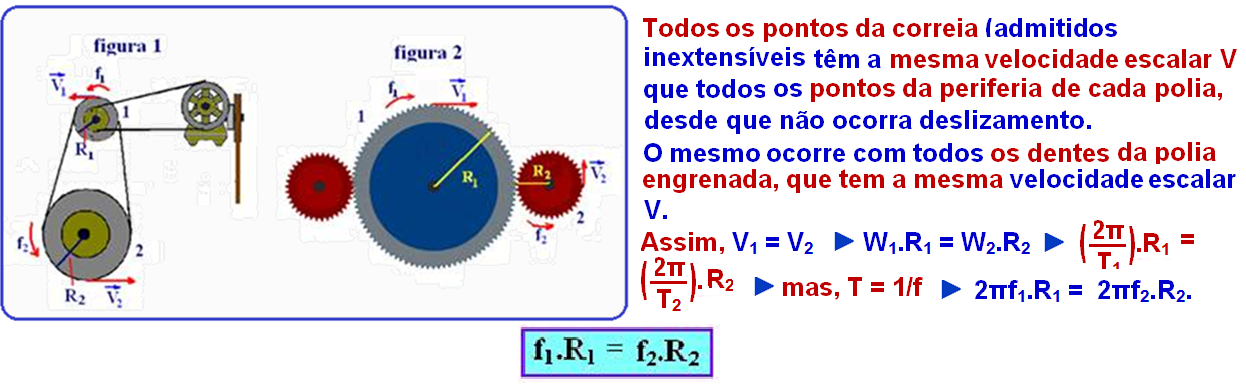

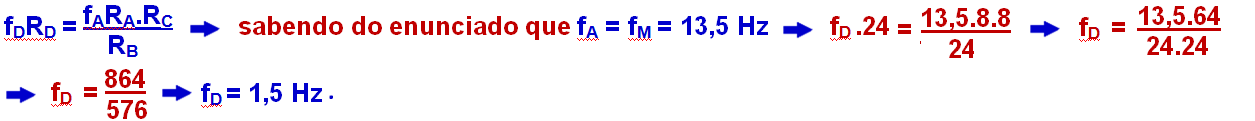
R- A
05-
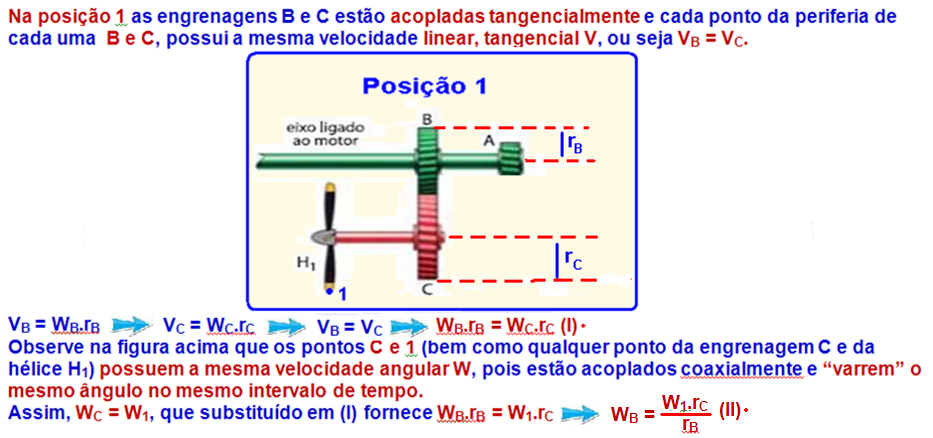

06-

07-
01-
02-


03-