Equação da Continuidade – Teorema de Bernoulli – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Equação da Continuidade – Teorema de Bernoulli
01- A vazão é a mesma – regime estacionário — R- B
02- S=100cm2=102.10-4 — S=10-2m3 — Z=7.200L/h=7.200/3.600L/s=2.L/s — Z=2.10-3m3/s — Z=S.v — 2.10-3= 10-2v — v=2.10-3/10-2 — v=0,2m/s — R- C
03- ΔV=18.10.2=360m3 — Δt=10h — S=25.10-4m2 — Z=ΔV/Δt=360/10 — Z=36m3/h — Z=S.v — 36=25.10-4.v — v=36/25.104 — v=14.400m/h — v=14.400/3.600=4m/s — R- D
04- O jato de ar que se move com velocidade v, paralelamente ao extremo (A) de um tubo que está imerso em um líquido, faz com que a pressão aí diminua em relação ao extremo inferior (ponto B) do tubo.
A diferença de pressão entre os pontos A e B empurra o fluido para cima. O ar rápido também divide o fluido em pequenas gotas, que são empurradas e se espalham para a frente — R- E
05- R- C — veja exercício anterior
06- Vazão — Z=0,01m3/s=10-2m3/s — volume total — ΔV=10×1.500=15.000L=15.103.10-3 — ΔV=15m3 — Z= ΔV/ Δt — 10-2=15/ Δt — Δt=1.500s=25min — R- C
07- R- B — veja teoria
08- Veja a figura abaixo:
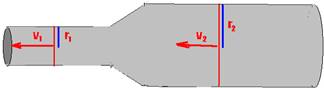
d2=2d1 — r2=2r1 — S1v1=S2v2 — π(r1)2.v1=π(r2)2.v2 — (r1)2.v1=(2r1)2.v2 — (r1)2.v1=4(r1)2.v2 — v1=4v2 — R- E
09-
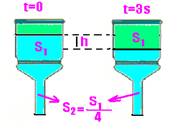
v1=Δh/Δt=9/3 — v1=3cm/s — S1=4S2 — S1.v1=S2.v2 — 4S2v1=S2.v2 — 4.3=v2 — v2=12cm/s
10- Maior área de seção transversal (1), menor velocidade, maior pressão — R- C
11- (01) correta – “os acréscimos de pressão sofridos por um ponto de um líquido em equilíbrio são transmitidos integralmente a todos os pontos do líquido e das paredes do recipiente que o contém” — Princípio de Pascal.
(02) Falsa, a vazão é a mesma, quem aumenta é a velocidade de saída da água.
(04) Falsa — Observe na equação P + d.v2/2=constante que a pressão P é inversamente proporcional à velocidade v, ou seja, quanto menor a área, maior a velocidade e menor a pressão.
(08) Correta – é a pressão atmosférica – Veja (01)
(16) Correta – a partir da saída, as partículas de água ficam sujeitas à força peso, desprezando-se a resistência do ar, e descrevem um arco de parábola.
( 01 + 08 + 16) = 25
12- (01) Correta – P=dgh (teorema de Stevin) — como h diminui, com d e g constantes, a pressão P também diminui.
(02) Falsa, é a pressão atmosférica.
(04) Correta – a pressão no ponto B (pressão atmosférica) é maior que a pressão no ponto A.
(08) Correta – veja (04)
(16) Falsa — PA=PB e PC=PD — mesmo nível horizontal – teorema de Stevin
(01 + 04 + 08) = 13
13- Zconstante=SA.vA = SB.vB — SA.v=SB.2v — SA=2SB — R- B
14- A vazão total das duas torneiras é Z=5L/min + 3L/min=8L/min — Z=8.10-3m3/min — Z=S.v — 8.10-3=0,8.v —
v=10-2m/min — v=1cm/min — R- C
15- A vazão é sempre a mesma independente da espessura da mangueira — no lançamento horizontal a velocidade v é a mesma e trata-se de um movimento uniforme de equação — S=So + vt — S=v.t — se o alcance S é quadruplicado, a velocidade v também é quadruplicada — S1.v1=S2.v2 — π.(R1)2.v=π.(R2)2.4v — (R2)2/(R1)2=1/4 — R2=R1/2 —
R- C
16- a) Z=S.v=πR2.v=3,14.12.33 — Z=104cm3/s — Z=0,104L/s (transporta 0,104 litros em cada 1 segundo)
b) Z=ΔV/Δt — 0,104=5/Δt — Δt=48s
17- Comprimento da canal — s=4m — tempo de percurso — t=1min=60s — velocidade da água

— v=s/t=4/60 —V=1/15m/s — área de seção transversal do canal — R=1m — S=πR2/2=π.(1/2)2/2 — S=π/8 — vazão — Z=S.v=(π/8).(1/15) — Z=π/120m3/s (m3.s-1) — R- E
18- I- Correta – Teorema de Stevin (P=d.g.h) – todos os pontos de um mesmo líquido (mesma densidade) localizados num mesmo nível horizontal (no caso,mesma altura), suportam a mesma pressão.
II- Falso – estão em alturas diferentes — PB<PA
III- Correta – viscosidade é definida como a resistência que um fluido oferece ao seu próprio movimento. Quanto maior for a sua viscosidade, menor será a sua capacidade de escoar (fluir) e maior será a força de atrito entre o fluido e as paredes do recipiente onde ele está escoando
IV- Correta – correta – veja teoria
R- D
19- a) Z=S.v=200.1 — Z=200m3/s
b) Z=S.v — 200=40.v — v=5,0m/s
20- a) 10L -1h — 150L – t h — t=15h
b) Z=ΔV/Δt=10.10-3m3/1h — Z=10-2m3/h — Z=S.v — 10-2=5.10-1.v — v=2,0.10-2m/h
21- Vazão — Z=S.v=2,5.30 — Z=75cm3/s — Z=ΔV/Δt — 75=5,4.103/Δt — Δt=5,4.103/75=0,072.103 — Δt=72s
22- Z=v.S=√(2gh).S=√(2.10.5).3.10-4=10.3.10-4=3.10-3m3s — Z=3L/s — R- B
23- Equação de Bernoulli — tubulação horizontal – h=0 — só tem energia cinética — P1+ dv12/2=P2 + dv22/2 —
1,5.105 + 103.(2)2/2=P2 + 103.(8)2/2 — 152.103=P2 + 32.103 — P2=152.103 – 32.103 — P2=120.103=1,2.105N/m2 —
R- A
24- SA=2SB — SA.VA=SB.VB — 2SB.5=SB.VB — VB=10m/s — teorema de Bernoulli — PA + d.g.hA + d.(VA)2/2 =
PB + d.g.hB + d.(VB)2/2 — 7.103 + 8.102.10.10 + 8.102.(5)2/2=PB + 8.102.10.1 + 8.102.(10)2/2 — 7.103 + 80.103 + 10.103=PB + 8.103 + 40.103 — 97.103=PB + 48.103 — PB=49.103=4,9.104N/m2
25- a) v=180km/h/3,6=50 — v=50m/s — redução da pressão — ΔP=ρv2/2=1,2.(50)2/2 — ΔP=1,5.103N/m2
b) variação de pressão=força/área — ΔP=peso/S — 1,5.103=m.10/5.400 — m=81.104kg — m=8,1.102t
c) ρv2/2=ΔP=peso/área — 1,2.v2/2=m.g/5.400 — 1,2.v2/2=250.103.10/5.400 — v=√771,6 — v=27,77m/sx3,6 — v=100km/h
26- Z=v.S=√(2gh).S=√(2.10.5).2.10-4 — Z=√100.2.10-4 — Z=2.10-3m3/s
27- a) entrada — PA=4.105N/m2 — RA=2/1=1cm=10-2m — hA=0 — vA=1,5m/s — segundo andar — PB — RB=1/2=0,5.10-2=5.10-3m — hB=5m — SA.vA=SB.vB — π.(RA)2.vA=π.(RB)2.vB — (10-2)2.1,5=(5.10-3)2.vB —
1,5.10-4=25.10-6.vB — vB=1,5.10-4/25.10-6 — vB=0,06.102 — vB=6m/s
b) Bernoulli — PA + d(vA)2/2 + d.g.hB = PB + d(vB)2/2 + d.g.hB — 4.105 + 103.(1,5)2/2 + 10.10.0 = PB + 103(6)2/2 + 103.10.5 — 40.104 + 0,1125.104 + 0 = PB + 1,8.104 + 5.104 — PB=40,1125.104 – 6,8.104 — PB=33,3.104=3,3.105Pa
c) vazão — Z=SB.vB=π.(RB)2.6=3,14.(5.10-3)2.6 — Z=471.10-6=4,71.10-4 — Z=4,71.10-4m3/s ou Z=0,471L/s
28- a) Falsa – se as alturas estivessem no mesmo nível, as velocidades do vento em cada uma delas seriam iguais e, assim não haveria diferença de pressão para empurrar o ar, não havendo ventilação dentro da toca.
b) Correta – o arbusto diminui a velocidade do vento na abertura 1 aumentando, nela, a pressão. Assim, a diferença de pressão entre as aberturas será aumentada, favorecendo a ventilação.
c) Como as alturas são constantes, a diferença de energia potencial gravitacional também é constante — P1 + dv12/2= P2 + dv22/2 — ΔP= P1 – P2=d/2(v22 – v12) — ΔP é diretamente proporcional à diferença do módulo do quadrado das velocidades — Falsa.
d) Correta – ocorre da abertura de menor velocidade do vento, maior pressão (abertura 1) para a abertura de maior velocidade do vento, menor pressão (abertura 2)
29- a) Δt=1min e 40s=60 + 40 — Δt=100s — ΔS=20m — v=ΔS/Δt=100/20 — v=5m/s — vazão — Z=ΔV/Δt
=500.10-3/100 — Z=5.10-3m3/s — energia utilizada para elevar a água a uma altura h=20m num local onde g=10m/s2 — ΔW=dgh=103.10.20 — ΔW=2.105J — Poútil=ΔW.Z=2.105.5.10-3 — Poútil=1.000W (J/s) — rendimento (η=Poútil/Pototal) — 0.5=1.000/Pototal — Pototal=2.000W
b) V=S.h — 5.10-1=2.h — h=0,25m — P=dgh=103.10.0,25 — P=2,5.103N/m2
30- Z=400cm3s=4.102.10-6 — Z=4.10-4m3s — S1=2.10-4m2 — S2=10-4m2 — Z — constante — Z=S1.v1 —
4.10-4=2.10-4.v1 — v1=2m/s — Z=S2.v2 — 4.10-4=10-4v2 — v2=4m/s — Stevin em 2 — P2=d.g.h=103.10.0,5 —
P2=5.103N/m2 — h=o — dgh=0 — Bernoulli — P1 + d(v1)2/2=P2+ d(v2)2/2 — P1 + 103.4/2=5.103 + 103.16/2 —
P1=13.103 – 2.103 — P1=11.103N/m2 (N.m-2) — R- A
31- Veja a figura abaixo — BL — bomba no lençol — BS — bomba no solo — trabalho (energia)
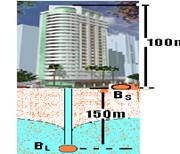
para elevar a água a uma altura h — W=d.g.h — potência útil — Pu=W.Z — Pu=d.g.h.Z — BS – PuS=103.10.100.0,03 =3.104= =3.104.1/750 — PuS=40 hp — rendimento de 80% — η=Pu/Pt — 0,8=40/Pt — PtS=50 hp — BL — bomba no lençol — PuL=d.g.h.Z=103.10.250.0,03 — PuL=100 hp — η= PuL/PtL — 0,8=100/PtL — PtL=125 hp — utilizando o compressor — hcompressor=1,5hBS — Pucompressor=1,5.PuBS — Pucompressor=1,5.40 — Pucompressor=65 hp —
η=Pucompressor/Ptcompressor — Ptcompressor=75 hp — 0) Falsa — deverá ser de 125 hp — 1) verdadeira — 2) verdadeira — 3) verdadeira — 4) verdadeira
32– P=d.g.h.Z=d.g.h.ΔV/Δt — P=0,5cv=0,5.750 — P=375W — 375=103.10.15.500.10-3/Δt — Δt=75.000/375=200s — R- B
33- Apenas a afirmação II é incorreta, pois os pontos A e B estão no mesmo líquido, mas em alturas distintas e logo pela Lei de Stevin estão sob pressões diferentes.
R- D — veja teoria
34- Você pode chegar à opção correta sem apelar para equações ou leis da Física, mas apenas se baseando em fatos do cotidiano — quando você joga água no jardim ou lava o carro com uma mangueira convencional, você coloca o polegar na extremidade de saída da água para diminuirmos a área de fluxo — isso, consequentemente, provoca um aumento de pressão e um aumento na velocidade, lançando a água à maior distância — fisicamente você pode usar a equação da continuidade e a equação de Bernoulli — sendo Q a vazão, v a velocidade do fluxo e A a área da secção transversal, a equação da continuidade — Q = v A. (I) — a equação de Bernoulli relaciona o acréscimo de pressão (p) com a altura de bombeamento (h) e com a velocidade de fluxo (v) —
considerando o sangue um fluido incompressível de densidade d e que seja bombeado a partir do repouso, desprezando perdas nas paredes — p=mV2/2 + mgh (II) — observando a equação (I) você conclui que, se a vazão é constante, diminuindo-se a área de fluxo a velocidade aumenta — na equação (II), se a velocidade aumenta, a pressão também aumenta.
Analisando as opções:
a) Falsa — pelo exposto acima.
b) Falsa — as forças mencionadas formam um par ação-reação.Essas forças nunca se anulam, pois agem em corpos diferentes.
c) Falsa — a pressão de 2,5 Pa significa que é exercida uma força de 2,5 N em 1 m2.
d) Correta.
e) Falsa — considerando a densidade do mercúrio, dHg = 13,6 g/cm3 = 13,6.103 kg/m3 (não fornecida no enunciado), a pressão sistólica de 120 mmHg = 0,12 mHg, pode ser calculada no Sistema Internacional pelo teorema de Stevin:
p = dHg g h = 13,6.103.10.0,12 — p = 1,6.103 Pa — R- D
35- Dados: V = 1.200 L; h = 30 m; L = 200 m — seguindo as instruções do fabricante, entremos com os dados na tabela para obtermos o valor de H.
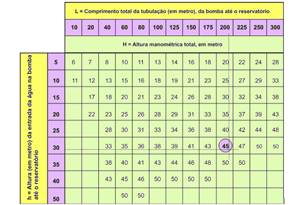
Como mostrado, obtemos H = 45 m — analisando o gráfico dado, temos os valores mostrados: H = 45 m — Q = 900 L/h.
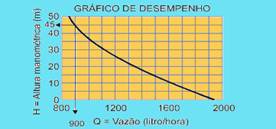
Calculando o tempo para encher o reservatório — Q=V/t — 900=1.200/t — t=1.200/900 — t=4/3h — t=80min —
t=1h e 20min — R- E
36- Tempo total do banho — Δtt = 6 min e 54 s = 414 s = 6,9 min — tempo com um quarto de volta — Δt1 = 1 min e 18 s = 78 s = 1,3 min — tempo com o registro fechado — Δt2 = 3 min e 36 s = 216 s = 3,6 min — tempo com vazão total — Δt3 = ? —
soma dos tempos — Δtt = Δtt + Δt2 + Δt3 — 6,9 = 1,3 + 3,6 + Δt3 — Δt3=2 min — cálculo do consumo de água, usando os dados da tabela — Cágua = 1,3×1,5 + 2×10,8 = 1,95 + 21,6 — Cágua = 23,55 L — R- B
37- Cálculos feitos na questão anterior — o chuveiro ficou ligado durante um curto intervalo de 78 s, despejando 1,95 L — a seguir, ficou fechado durante 216 s e, finalmente, com vazão total durante 120 s, despejando 21,6 L — fazendo essas comparações — R- C
38- Artérias: são vasos de maior calibre que os demais, de parede espessa que saem do coração levando sangue para os órgãos e
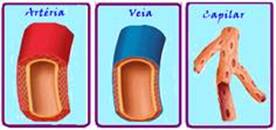
tecidos do corpo — capilares sangüíneos: são vasos de pequeno calibre que ligam as extremidades das artérias às veias — as veias levam o sangue vindo do corpo, ao coração e suas paredes são mais finas que as das artérias — a artéria Aorta é a maior do corpo humano, pois além de ser a maior em extensão, ela é a de maior (espessura, diâmetro) calibre — observe que o vaso I possui maior área (espessura, diâmetro) que o de cada vaso II, então ele só pode ser a artéria aorta — o fluxo de sangue no corpo humano é constante, ou seja, em cada vaso, o volume que circula no mesmo intervalo de tempo é o mesmo — φI = φII —
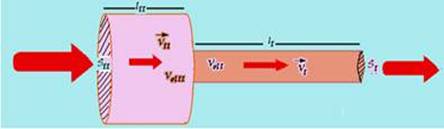
VolI/∆t = VolII/∆t — (S1.lI)/ ∆t = SII.lII/∆t (1) — a velocidade do sangue no interior de cada vaso é diferente e vale — V1=lI/∆t (2) — V1I=lII/∆t (3) — comparando (1) com (2) e com (3) — SI.VI = SII.VII — 240.30 = 240000V2 — V2=2700/240000 —
V2=0,03cm/s — R- C
