WHEATSTONE BRIDGE – RESOLUTION
Commented resolution of entrance exam exercises on
Galvanometer as Ammeter and as Voltmeter – Wheatstone Bridge
01- The full-scale current (i G ) of the galvanometer remains the same — what changes is the full-scale current (I) of the system (galvanometer + shunt resistance in parallel with it), which works as an ammeter, indicating a current greater than i G — R- B
02- Observe the figure below — U=U G ( 1 + R M /R G ) — 10=1(1 + R M /10) — R M =90Ω
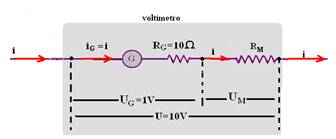
Of course the multiplication factor is 10 (a full scale voltage of 1V should indicate 10V) — R- A
03- U=U G (1 + R M /R G ) — 100=20(1 + R M /2,000) — R M =8,000Ω=8kΩ — R- D
04- a) i=i G (1 + R g /R S ) — 50.10 -3 =2.10 -3 (1 + 100/R S ) — 24=100/R s — R S =4.2Ω (connected in parallel with the galvanometer)
b) See figure below — U=U G + U M — 20=R G .i G + R M .i M — 20=100.0.002 + R M .0.002 — 20=0.2 + 0.002R M —
R M =9,900Ω — (connected in series with the galvanometer)
05 – the multiplication factor is n=10 — I=ni G — I=10.I G — i G =I/10 — n=1 + R G /R S — 10=1 + R G /R S — R S =R G /9 —
R-B
06- U=R G .i + R M .i — 10=0.5.10 -3 + R M .10 -3 (/10 -3 ) — 10 4 =0.5 + R M — R M ≈10 4 Ω in series with the galvanometer
07- U=U G + U M1 — 1=100.10 -4 + R 1 .10 -4 (/10 -4 ) — 10 4 = 100 + R 1 — R 1 =10,000 – 100 — R 1 =9,900Ω — R 1 =9.9.10 3 Ω —
U R2 =10 – 1=9V — R 2 =U R2 /i=9/10 -4 — R 2 =9.10 4 Ω — U R3 =100 – 10=90V — R 3 =U R3 /i=90/10 -4 — R 3 =9.10 5 Ω —
R-C
08- I=i G (1 + R g /R S ) — 4.5=3(1 + R G /R S ) — 4.5=3 + 4.5/R S — r=R S =3 ,0Ω — R-B
09- Fan C , as it is a Wheatstone bridge, does not pass electric current between points P and Q which are under the same potential difference, that is, V P = V Q
10- This is a Wheatstone bridge, with no electric current passing between points C and D, which are under the same potential difference, i.e. C C = V D — R- C
11- When the galvanometer indicates zero, the bridge is in balance — 150.R=300.(RR 1 )/(R + R 1 ) — 150R 2 + 150.RR 1 =300R.R 1 — 150R=150R 1 — R 1 =R — R- B
12- Length-resistance relationship — 50Ω – 500mm — PΩ – 350mm — 500P=50,350 — P=35Ω — Q=50 – 35 — Q=15Ω
(R 2 + P).R 1 =QX — (30 + 15).210=35.X — X=270Ω — R- E
13- a) R=R o (1 + αθ) — 108=100(1 + 4.10 -3 θ) — 1.08 – 1=4.10 -3 θ — θ=8.10 -2 /4.10 -3 — θ=20 the C
b) RR 1 =R 1 .R 2 — R=R 2 =108Ω — R=U/i — 108=U/5.10 -3 — U=1,080.10 -3 — U=1.08V
14- If the current in the galvanometer is zero, the current i 1 that passes through R 4 is the same that passes through R 1 and the current i 2 is the same in R 3 and R 4 — U CA = U CB — R 4 i 1 = R 3 i 2 — U AD = U BD — R 1 i 1 = R 2 i 2 — R- C
15- a) 3.2=1.X — X=6Ω
b) Observe the sequence below
R eq =8/3Ω — R eq =U/i — 8/3=12/i — i=36/8 — i=4.5A
16- L 1 .(200 parallel with 200)=L 2 .R X — 20,100=50.R X — R X =40Ω
17- a) Assuming the ammeter and voltmeter are ideal — removing the voltmeter and short-circuiting the ammeter — figure below —
The ammeter indicates i=5.0.10 -3 A
b) Voltage that the generator supplies to the circuit — U=E – ri=10 – 500.0.005 — U=7.5V — see the diagram below —
U AB =V A – V B =1.000×0.0025 — V A – V B =2.5V — V B =V A – 2.5 — U AD =V A – V D =2.000×0.0025 — V A – V D =5V —
V D = V A – 5 — as the voltmeter is inserted between points B and D, U BD is of interest — U BD = V B – V D =(V A – 2.5) – (V A – 5) —
U BD =V A – 2.5 – V A + 5 — U BD =2.5V — the voltmeter indicates 2.5V
18- If V A = V B the ddp between points A and B of the circuit is zero and the Wheatstone bridge is in equilibrium — 120.R = 90.60 — R = 45Ω
19- Note that no current passes between C and D — the bridge is in balance — if U AB = 100V and U AC = 50V, U DB = 50V — see
diagram below
R- 50V
20- Note that this is a Wheatstone bridge that is in balance ( equal resistors ) — points B and D have the same potential — R- V B = 6V
21- If the galvanometer indicates zero, the bridge is in balance and the following relationship is always valid, regardless of the voltage —
15.(10 + 5)=5.(20 + R) — 225=100 + 5R — R=125/5 — R=25Ω — R- A
22- There are two bridges in balance — bridge where the ammeter A 1 is — 20.20=10.R 1 — R 1 =40Ω — the circuit, then, is —
R-B
23-(AFA)
With the Ch switch closed, note that since the wires are ideal and the bulbs are identical (same resistance), bird III is
in a wire where no electric current passes (balanced Wheatstone bridge) — thus, no current will pass through birds II and IV, as the wires are ideal and there will be no potential difference between their legs — there is a potential difference between the legs of bird I and, through it, electric current will pass — R-C