|
|
RESOLUÇÕES
Questão 1.
01- P --- Pode ser resolvida pela segunda lei de Kepler (lei das áreas) de enunciado: “ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais aos tempos gastos para percorrê-las”
Então:
A1/∆t1 ~A2/∆t2=constante=K
Essa constante K depende do planeta e recebe o nome de velocidade areolar
Observe na expressão acima que quando A1=A2 --- ∆t1= ∆t1, ou seja, para o arco maior 34, ser percorrido no mesmo
intervalo de tempo que o arco menor12, a velocidade em 3,4 (mais perto do Sol - periélio) deve ser maior que a velocidade em 1,2 (mais afastado do Sol – afélio).
Portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio --- como a força resultante sobre o cometa é o produto de sua massa pela sua aceleração e como a aceleração é maior no afélio (ponto P), a força resultante sobre ele no afélio (ponto P) deverá ser maior --- ou ainda, a intensidade da força resultante sobre o cometa corresponde à força de atração gravitacional entre ele e o Sol, fornecida por FR=G.M.m/r2 --- veja que, como G,M e m são constantes, a intensidade da força resultante sobre o cometa é inversamente proporcional à distância r e, como no afélio r é menor, nele a força resultante terá maior intensidade.
02- Não --- observe na
expressão da quantidade de movimento 
= m.
que o vetor quantidade de movimento
depende do vetor
velocidade que, em
qualquer ponto da trajetória do cometa é sempre tangente à mesma e, portanto
tem sempre a direção e sentido variando em cada ponto (o mesmo acontece com ) --- a intensidade de e consequentemente de também variam, pois o
movimento do cometa tem aceleração ( acelera
do afélio para o periélio e retarda do periélio para o afélio) com a
intensidade da velocidade aumentando e diminuindo.
Questão 2
01- Como o enunciado pede para considerar o sistema água e gelo isolado haverá trocas de calor somente entre eles e, ao final dessas trocas você terá apenas água líquida à temperatura de equilíbrio térmico θe --- Q – quantidade de calor cedido pelos 200g de água a 25oC para sua temperatura passar de 25oC a θe --- Q=m.c.(θe – θ)=200.1.(θe – 25) --- Q=200.θe – 5000 --- Q’ – calor recebido pelos 50g de gelo a 0o para mudar de estado e se transformar em 50g de água a 0oC --- Q’=m.L=50.80 --- Q’=4000cal
Q’’ - calor absorvido pelos 50g de água a 0oC a 50g de água a θe --- Q’’=m.c.(θe – 0)=50.1.θe --- Q’’=50.θe --- a soma algébrica dessas quantidades de calor trocadas pelo sistema é nula --- Q + Q’ + Q’’ = 0 --- 200.θe – 5000 + 4000 + 50.θe=0 ---
250.θe = 1000 --- θe=4oC
02- Maior --- você pode, agora incluindo o copo nas trocas de calor, efetuar o equilíbrio térmico entre toda a água (250g) a 4oC com o copo que está a 25oC e, é claro que a temperatura final estará entre 4oC e 25oC, ou seja, será maior que 4oC.
Questão 3
01- Como as ondas emitidas pelos dois alto-falantes estão em fase elas possuem a mesma freqüência (f), o mesmo comprimento de onda (λ), e mesma amplitude (A) e em fase (ambas para cima ou ambas para baixo) --- nos pontos O e M as ondas estão em concordância de fase (som de intensidade máxima, reforço) --- para o ponto M, onde as ondas estão em concordância de fase (interferência construtiva), a distância de uma fonte até M (d2=10m) menos a distância da outra fonte até M (d1=8m), deve valer um comprimento de onda 1λ --- d2 – d1=1λ --- 10 – 8=1λ --- λ=2,0m.
02- Mais próxima --- como V=λ.f e como V é constante, o comprimento de onda λ e a frequência f são inversamente proporcionais --- assim, como entre O e M existe um λ, se a frequência aumenta, esse λ diminui e o ponto M ficará mais perto do ponto O.
Questão 4
01- Convergente --- no caso, os olhos do professor são objetos reais e você observando-os através da lente verá imagens maiores que os objetos (no caso os olhos do professor) --- então, as lentes dos óculos são lentes convergentes com o objeto entre o foco e a lente que, nesse caso conjugam imagens virtuais e maiores que os objetos --- não podem ser lentes divergentes, pois estas conjugam imagem sempre virtuais e menores que os objetos.
02-O professor tem hipermetropia e, nela, a formação da imagem ocorre, teoricamente, atrás da retina, porque o olho é curto
demais. e porque o cristalino não consegue se acomodar para focalizar a imagem sobre a retina --- os hipermétropes não
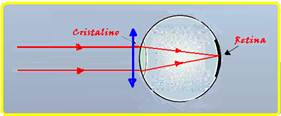
conseguem enxergar objetos próximos com nitidez --- o defeito é corrigido com lentes convergentes que aproximam a imagem colocando-a sobre a retina.
Questão 5
01- Igual --- os pontos B e C estão num mesmo ramo (em série), então a corrente elétrica que passa por cada um desses pontos é a mesma.
02- iA=iC + iD --- Primeira lei de Kirchhoff ou lei dos nós: “A soma algébrica das correntes que chegam a um nó é igual à soma
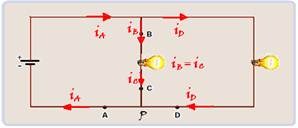
algébrica das correntes que saem do mesmo nó” --- observe na figura as correntes que chegam e que saem do nó P --- iA=iC + iD.
03- Igual --- sendo a resistência elétrica dos fios nula e como não há entre C e A nenhum dispositivo elétrico que provoque uma diferença de potencial entre esses pontos, essa ddp entre eles será nula, o que implica que eles possuem o mesmo potencial.
Questão 6
01- A luz do laser com velocidade de propagação c=3.108m/s, sai do fundo do vagão, percorre 30m e atinge um espelho na frente do vagão --- em seguida sofre reflexão no espelho, retorna se propagando por mais 30m e atinge o detector junto ao laser no fundo do vagão, demorando na ida e volta um intervalo de tempo ∆t e percorrendo ∆S=30 + 30 = 60m --- V=∆S/∆t ---
3.108=60/∆t --- ∆t=60/3.108 --- ∆t=20.10-8 --- ∆t=2,0.10-7s.
02- Pelo segundo postulado da teoria da relatividade especial de Einstein – A velocidade da luz no vácuo é sempre a mesma em qualquer referencial inercial de observação --- é invariável para qualquer mudança de referencial --- assim, no referencial de Alberto também será de 3,0.108m/s.