Resoluções das questões de Vestibulares recentes por assunto – 2017 – 2016 – 2015 – Óptica
Resoluções das questões de Vestibulares recentes por assunto – 2017 – 2016 – 2015 – Óptica
01- A velocidade das nanosondas corresponde a 20% da velocidade da luze terá valor 
V = 20% de 3.108 m/s V = 0,2×3.108 = 0,6.108 m/s V = 6.107 m/s.
Um ano-luz é a distância que a luz pode viajar em um ano com velocidade de 3.108 m/s. Por exemplo, em um ano-luz, a distância percorrida seria de aproximadamente 9.460.800.000.000 (nove trilhões, quatrocentos e sessenta bilhões e oitocentos milhões) de quilômetros, ou, aproximadamente 9.1015 m.
V =
∆S = 4,4×9.1015 = 39,6.1015 m 6.107 = 
∆t =
∆t = 6,6.108 s.
Ano em segundos 1 minuto = 60 segundos 1 hora = 60 x 60 = 3600 segundos 1 dia = 24h x 3600 = 86.400 segundos 365 dias = 31.536.000 segundos 1 ano tem aproximadamente 3,15.107 s.
∆t = 
21 anos
R- C
02-
Nós conseguimos resolver esse problema por semelhança de triângulos, observe a figura:
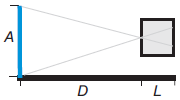
Os dois triângulos formados nessa figura são semelhantes, sendo assim:
O x é a altura da imagem, que será formada no fundo da câmera. Isolando ele:
Substituindo, o L está em cm (8 cm = 0,08 m) apenas dividir por 100:
Resolvendo:
x = 0,04 m = 4 cm
Alternativa B
03- Se você não domina a teoria, ela está a seguir:
Cor de um corpo
A luz branca do Sol ou de uma lâmpada qualquer é denominada luz policromática (várias cores) e é composta das cores monocromáticas (uma só cor), vermelho, alaranjado, amarelo, verde, azul, anil e violeta.
A cor apresentada por um corpo, ao ser iluminado, depende do tipo de luz que ele reflete difusamente (espalha em todas as direções e sentidos) e que chega aos olhos do observador.
Um corpo negro absorve todas as cores e um corpo branco reflete todas as cores.
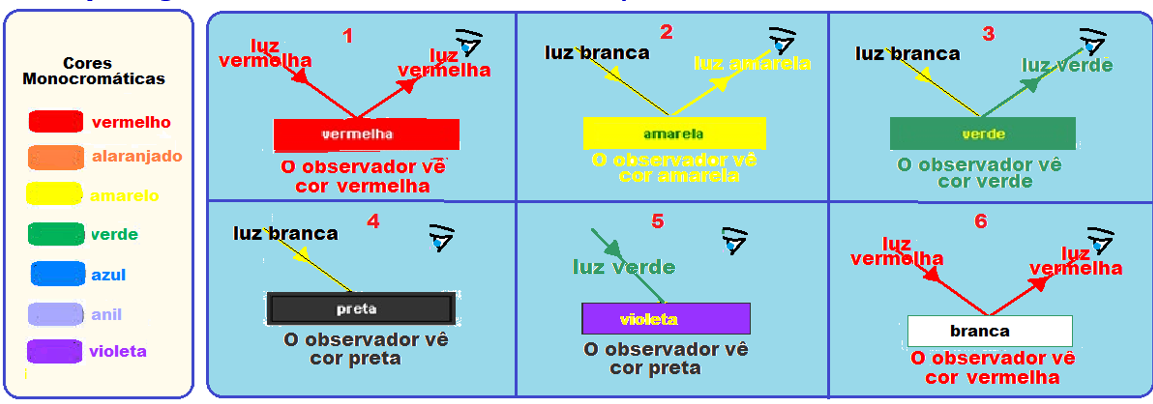
Figura 1 
O corpo vermelho reflete difusamente apenas a cor vermelha e o observador enxergará vermelho.
Figura 2 As sete cores (policromática branca) incidem sobre o corpo amarelo que reflete difusamente somente o amarelo e o observador enxergará essa cor.
Figura 3 As sete cores (policromática branca) incidem sobre o corpo verde que reflete difusamente somente o verde e o observador enxergará verde.
Figura 4 O corpo negro absorve todas as cores e nenhuma chegará ao observador que verá negro (ausência de cores).
Figura 5 O corpo violeta reflete difusamente somente o violeta e absorverá o verde, não chegando nenhuma luz ao observador, que verá negro.
Figura 6 O observador verá vermelho, pois o corpo branco reflete difusamente todas as cores inclusive o vermelho.
No caso do exercício, as palavras que você enxergará em azul são PRETO, VERDE e VERMELHO e as cores serão azul (as três palavras anteriores) e preta (as demais radiações serão absorvidas fornecendo a sensação visual de preto).
R- B
04-
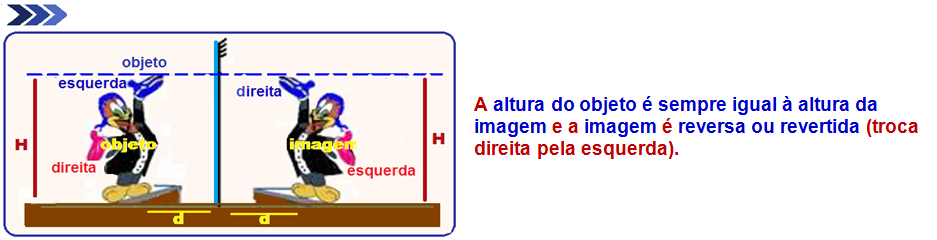
Características da imagem num espelho plano
O ponto objeto (O) e o ponto imagem (i) são simétricos em relação ao espelho, ou seja, a distância do
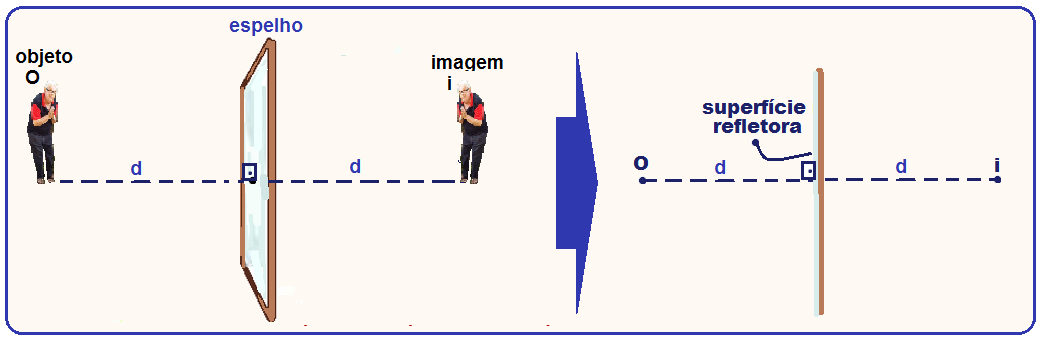
distância do objeto ao espelho é a mesma que a distância da imagem ao espelho e contidos numa mesma reta perpendicular ao plano do espelho.
R- C
05-
06-
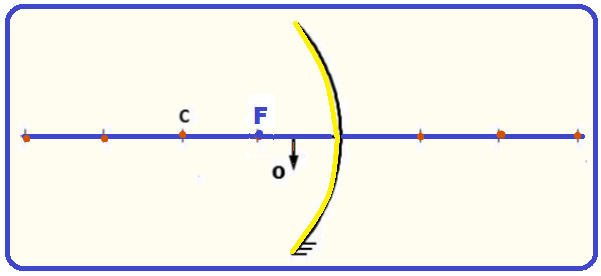
a) O foco F está localizado na distância média entre o centro de curvatura C e o espelho.
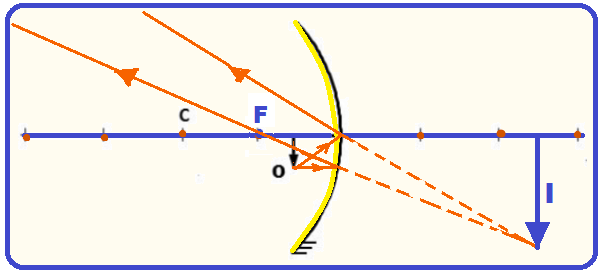
b)
c)
f = R/2 = 10/2 = 5 cm (positivo, espelho côncavo).
P = 3 cm
P’ = ?
Equação dos pontos conjugados 
= 
+ 
= 
+ – = 
= P’ = – 7,5 cm (P’ < 0, imagem virtual)
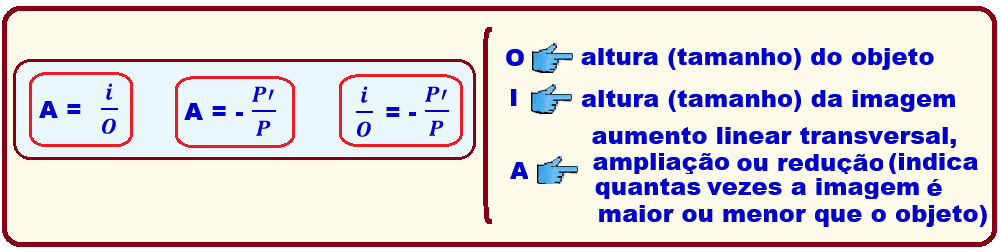
i= ?
o = – 2cm (invertida)
P = 3 cm
P’ = – 7,5 cm
= – 
= – 
i = 
= 5 cm ( a imagem é direita em relação ao objeto e tem 5cm de altura).
07-
08- Pelas características dos espelhos, podemos excluir algumas alternativas.
Por mais que um espelho plano ajudasse, ele não seria capaz de modificar a imagem, sendo assim não aumentaria seu campo de visão.
Um espelho côncavo converge os raios para um ponto, com isso não poderia ampliar o campo de visão do maquinista. Para um espelho ser considerado divergente ele precisa ter sua vergência negativa, quanto maior esse valor, em módulo, maior o campo de visão gerado.
Sendo assim, a alternativa B é a correta. Um espelho convexo aumenta o campo de visão, e se a vergência for grande mais expandido é esse campo visual.
R- B
09- O comportamento do balão de Natal como espelho é idêntico ao fornecido por um espelho esférico convexo, com as seguintes características:
Construção geométrica de imagens nos espelhos esféricos convexos
Espelho convexo 
Para qualquer localização do objeto Independentemente de sua posição, a
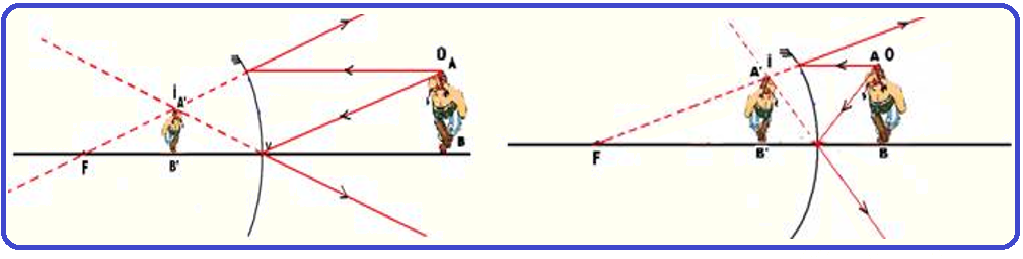
imagem terá sempre:
Natureza 
virtual
Localização atrás do espelho e entre V e F e observe nas figuras acima que à medida que o objeto se aproxima do espelho, a imagem também se aproxima e aumenta de tamanho, mas está sempre entre V e F.
Tamanho menor que o do objeto
Orientação direita em relação ao objeto
Utilidades: Os espelhos convexos são empregados como retrovisores em veículos, cabines de segurança, elevadores, etc.
Sua vantagem sobre o espelho plano, nesse particular, é ter maior campo visual. Têm, entretanto, o inconveniente de não darem noção da distância.
R- B
10-
11-
Na figura 1 a calota esférica está se comportando como um espelho esférico côncavo:
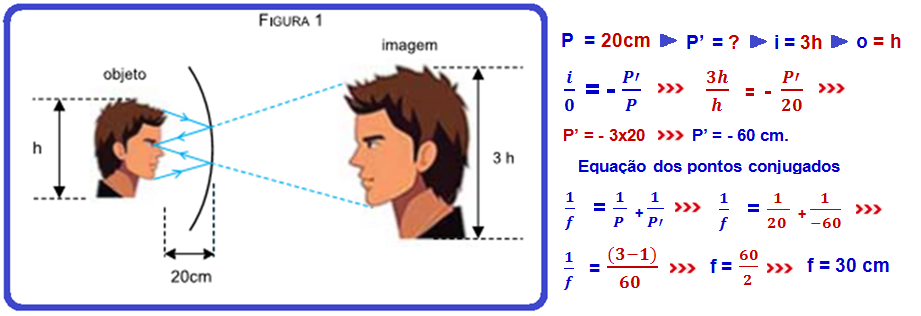
Módulo do espelho côncavo = módulo do espelho convexo = f = 30 cm.
b) Na figura 2 a calota esférica se comporta como um espelho esférico convexo de distância focal
f = – 30 cm (espelhos convexos possuem f < 0)
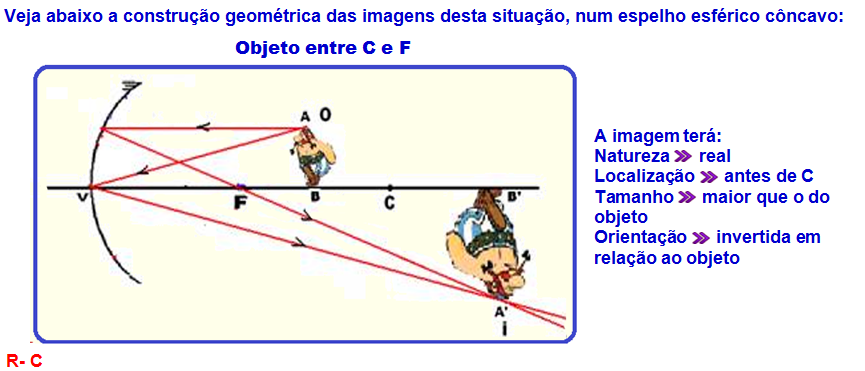
12- Podemos excluir de imediato o espelho plano, pois nele não há como se modificar a imagem. Uma imagem formada por um espelho convexo deve ser, obrigatoriamente, virtual e menor que o objeto. Por a imagem ser expandida dessa forma, só podemos trabalhar com um espelho côncavo de modo que a imagem seja virtual, conforme esquema abaixo.
Objeto entre o foco F e o vértice V ou entre o foco F e o espelho
A imagem terá:
Natureza virtual (obtida na interseção do prolongamento dos raios de luz ) não pode ser projetada, fotografada, etc., atrás do espelho.
Localização atrás do espelho
Tamanho maior que o do objeto
Orientação direita em relação ao objeto
Utilidades: são empregados com frequência quando se deseja obter uma imagem virtual e ampliada de um objeto, como é o caso dos espelhos de barbear, toalete, de dentista, espelho de otorrinolaringologia, etc.
R- B
13- 
Como o enunciado afirma que a imagem conjugada está situada no plano focal (f) do espelho 
a distância da imagem ao espelho P’ é a própria distância focal f do espelho P’ = f = 0,2 m.
= 
= 
i = – 
i = – 0,04m i = – 4 cm (a imagem tem altura de 4 cm e é invertida em relação ao objeto)
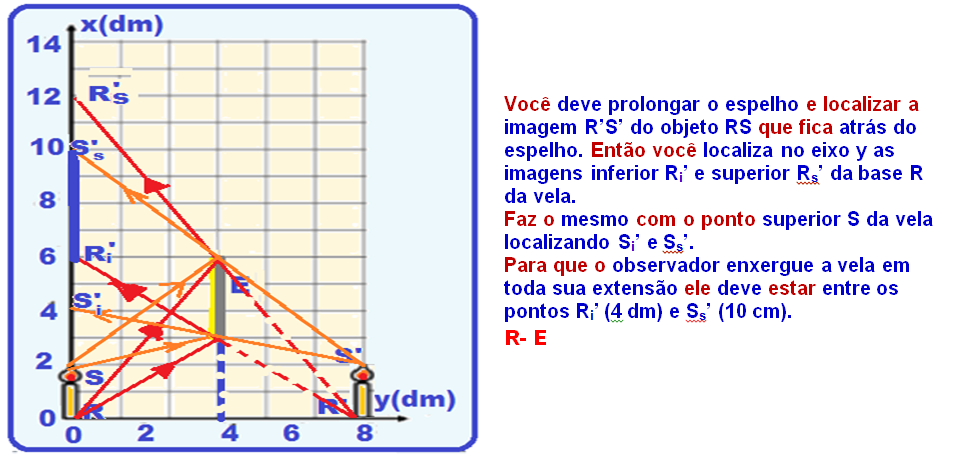
14- Veja abaixo a representação do raio de luz no plano cartesiano:
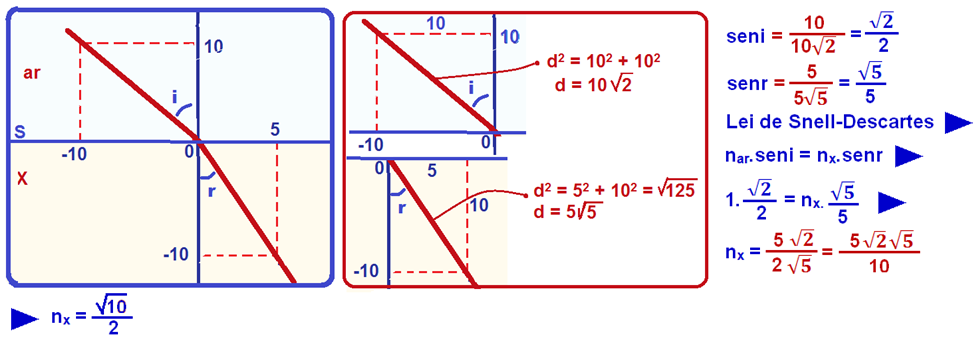
R- E
15- Vamos pensar em todas as alternativas:
No caso de A há uma refração, pois a luz passou de um ambiente para outro, o que não muda é o ângulo de refração.
Em B o ângulo é de 0°, pois está localizado em cima do eixo normal.
Na alternativa C, a frequência não muda quando se troca de ambiente, a velocidade se altera. Sendo assim, a alternativa D é a correta, pois quando se modifica a velocidade de propagação o comprimento de onda também se altera, basta analisar a fórmula abaixo:
Onde:
V é a velocidade de propagação
é o comprimento de onda
f é a frequência
16-
Lei de Snell-Descartes (refração da luz)
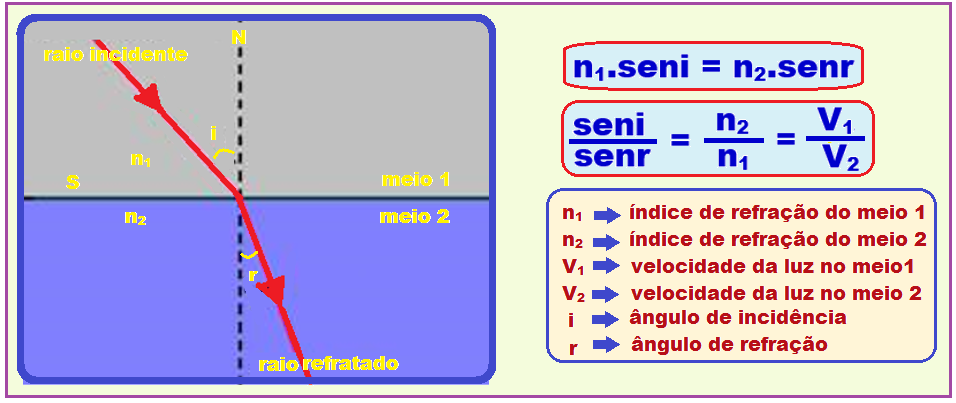
nar.sen45o = nágua.senr 
1.
/2 = 1,5.senr senr = 
= 
0,47 pelos valores
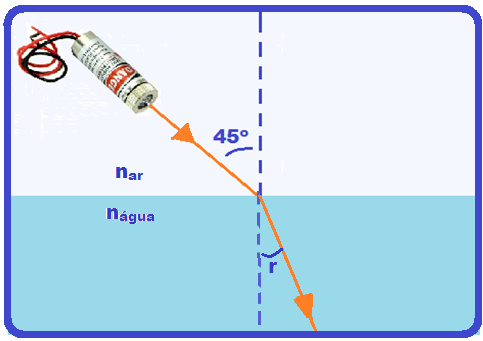
fornecidos no enunciado você observa que < 
, ou seja, menor que 30o.
R- A
17-
Vamos usar a imagem a seguir como apoio:
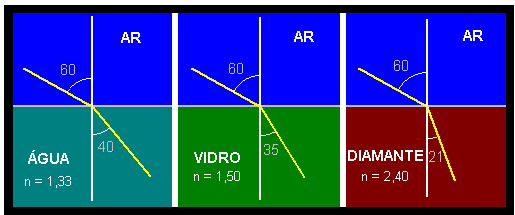
Nela podemos observar que quanto mais refringente (quanto maior o índice de refração), mais o raio refratado se aproxima da reta normal (reta que usamos de referência), no caso do exercício, a linha pontilhada. Ao observarmos o exercício, podemos concluir que o meio A tem que ser o lantânio, pois só assim há uma aproximação em um caso e um distanciamento no outro, já que ele é o valor intermediário. Ainda sobra o problema de B e C, que podemos concluir observando a imagem de apoio, que em B se trata de diamante (há uma aproximação à reta normal) e C se trata de vidro crown (há um afastamento à reta normal).
R – E
18-
a) O índice de refração absoluto aplicado ao material do cilindro constituído de um meio homogêneo e transparente é fornecido por:
n = 1,6 e c = 3.108 m/s 
n = 
1,6 = 
V = 
V = 1,875 m/s
b)
Aplicando a lei de Snell-Descartes na refração do feixe de luz em A, do ar para o cilindro nar.seni = n.senr 1.sen53o = 1,6.senr 1.0,8 = 1,6.senr senr = 
= 0,5 r = 30o.
Observe atentamente a figura abaixo:
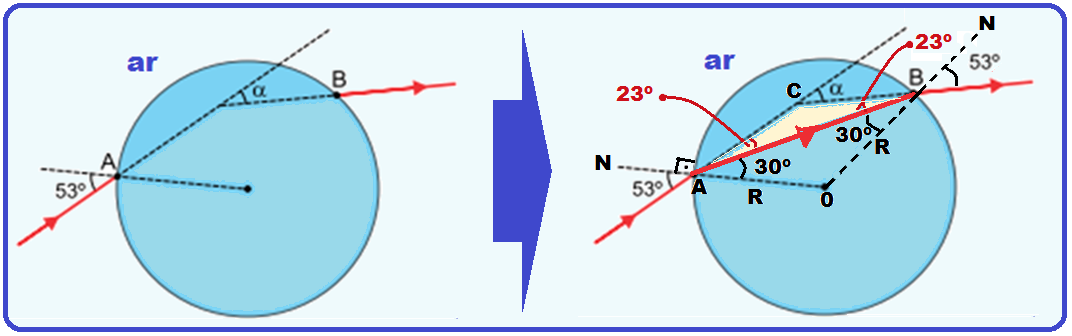
Se o ângulo de incidência (com a normal N) em A é de 53o, o ângulo de emergência em B (com a normal N) também será de 53o, pois os meios são os mesmos.
Como o triângulo AOB é isósceles (dois lados iguais R) então seus ângulos opostos são iguais (30o).
No triângulo ABC o ângulo α é externo o que implica que α = 2×23 = 46o
19- Breve teoria
Na figura 1 o ponto objeto real P está dentro da água (mais refringente, maior índice de refração) e emitindo dois raios de luz, um vertical que não sofre desvio e o outro oblíquo que, ao se refratar para o ar, afasta-se da normal atingindo os olhos do observador e determina a imagem virtual (P’), obtida no prolongamento desse raio e onde ele intercepta o raio de luz vertical, fornecendo essa imagem P’, acima do objeto real P.
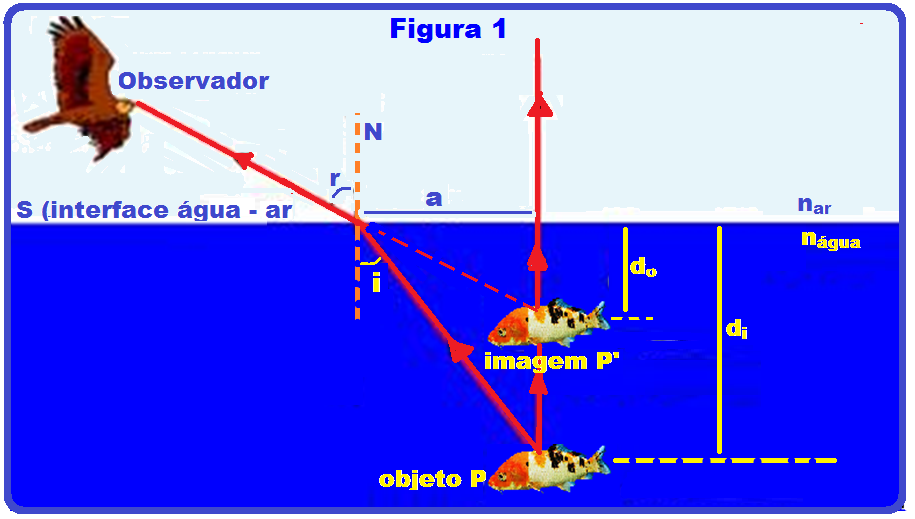
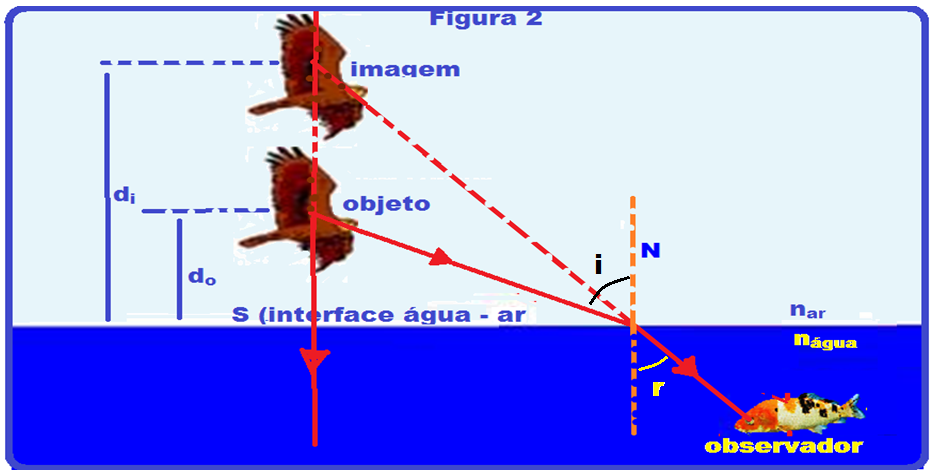
Na figura II o ponto objeto real P está no ar (menos refringente, menor índice de refração) e emitindo dois raios de luz, um vertical que não sofre desvio e o outro oblíquo que, ao refratar-se para a água aproxima-se da normal atingindo os olhos do observador e determina a imagem virtual P’, acima do objeto real P.
Observe que, em ambos os casos a imagem está sempre acima do objeto.
R- B
20- Veja na figura da esquerda os ângulos que confirmam que o ângulo de incidência do raio de luz na interface ar – líquido (ponto A) vale i = 60o.
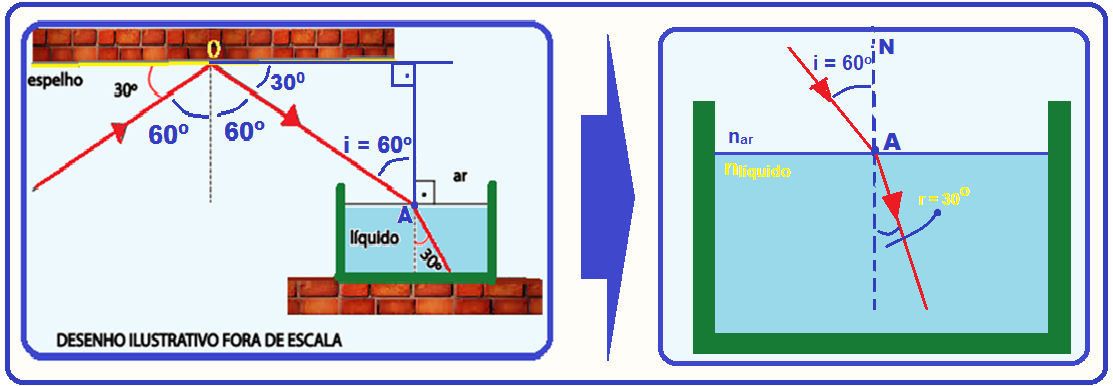
Aplicando a lei de Snell – Descartes na figura da direita acima no ponto Ada interface ar – líquido
Nar.seni = nlíquido.senr 
1.sen60o = nlíquido.sen30o 1.
= nlíquido. nlíquido =
R- C
21- Podemos resolver esta questão através da Lei de Snell-Descartes 
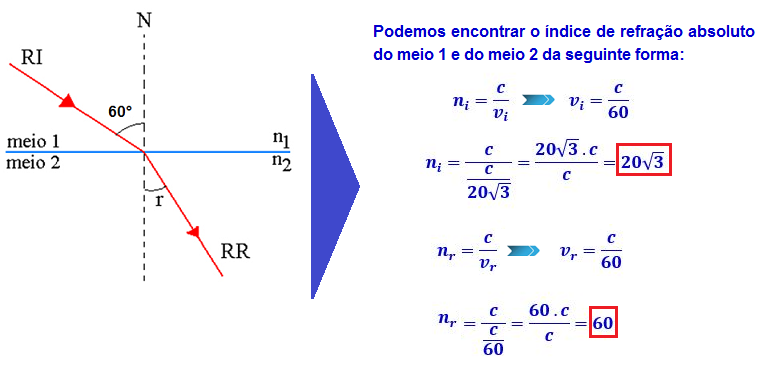
Temos, então, que 
R- Portanto, a resposta correta é a alternativa A.
22-
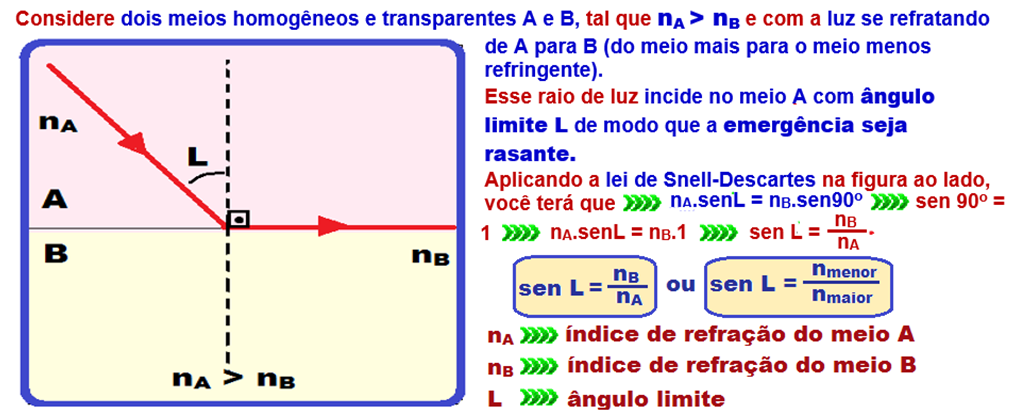
Os pontos do tubo retilíneo luminescente que podem ser vistos por pessoas fora da piscina são aqueles localizados abaixo do ponto M já que os pontos acima de M serão impedidos de se refratarem pela boia circular opaca.
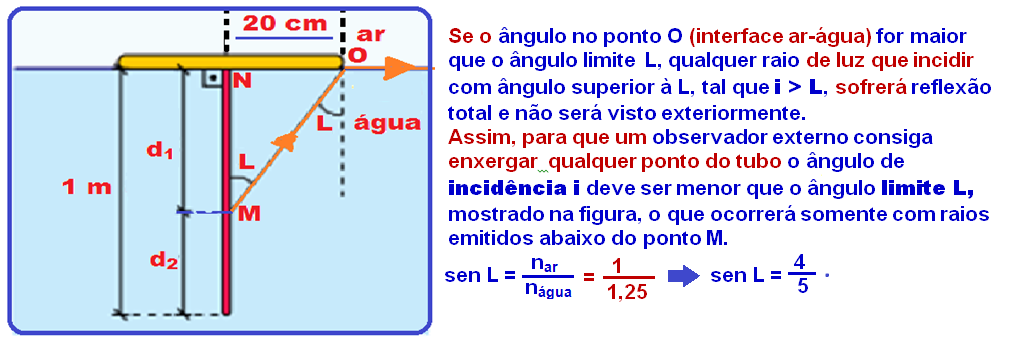
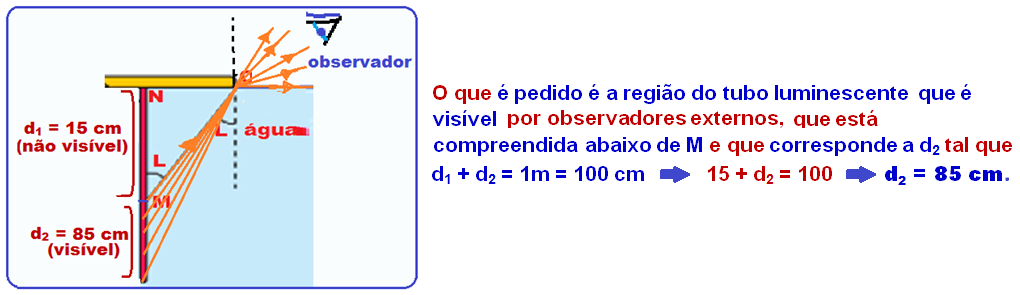
R – B
23-
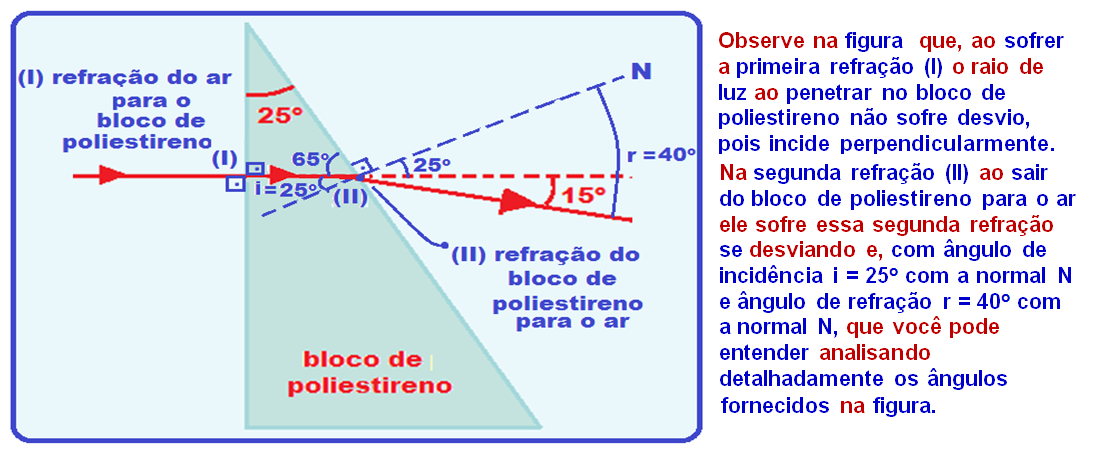
Aplicando em (II) a lei de Snell-Descartes 
npoliestireno.seni = nar .senr npoliestireno.sen25o = 1.sen40o npoliestireno.0,4 = 1.0,6 npoliestireno= 
npoliestireno = 1,5.
R- B
24-
Índice de refração
Observe na expressão acima que, sendo a velocidade c da luz constante, a velocidade v de propagação da luz no meio (no caso, o vidro) é inversamente proporcional ao índice absoluto de refração da luz nesse meio.
A dispersão luminosa ocorre artificialmente quando a luz se dispersa como no interior de um prisma (ou no interior da esfera de vidro do exercício) ou quando passa do ar para a água, sendo mais desviada a luz monocromática violeta (menor velocidade) e menos desviada a luz monocromática vermelha (maior velocidade).
Como, pelo enunciado, o índice refração absoluto do vidro é maior para a cor azul do que para a
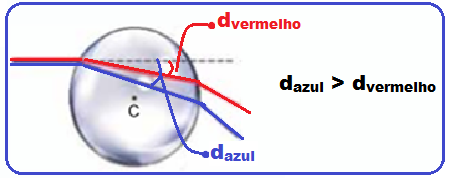
vermelha, a luz azul, no interior do vidro sofre maior desvio ao atravessar a esfera (veja figura acima).
R- B
25- A) Veja a equação de Gauss abaixo:
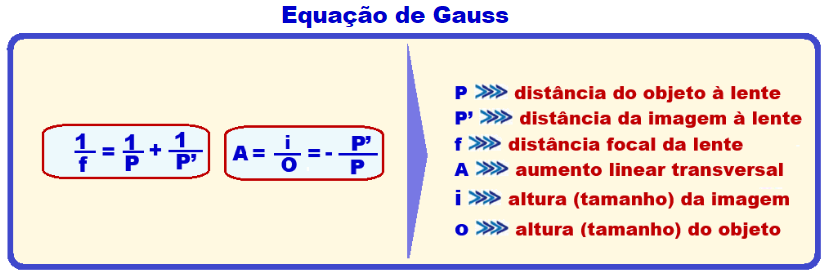
Sendo a lente a mesma, a distância focal f também é a mesma e aampliação A (aumento linear transversal) é fornecida pela expressão A = – que mostra que A depende apenas das distâncias do objeto e da imagem à lente.
Se a ampliação fosse a mesma nas duas posições, P1 seria igual à P1’, P2seria igual à P2’ e │A│= │1│(objeto e imagem teriam o mesmo tamanho).
Observe na figura que, com o objeto mais próximo da lente P1’ > P1 e│A1│> │1│(tamanho aumentado).
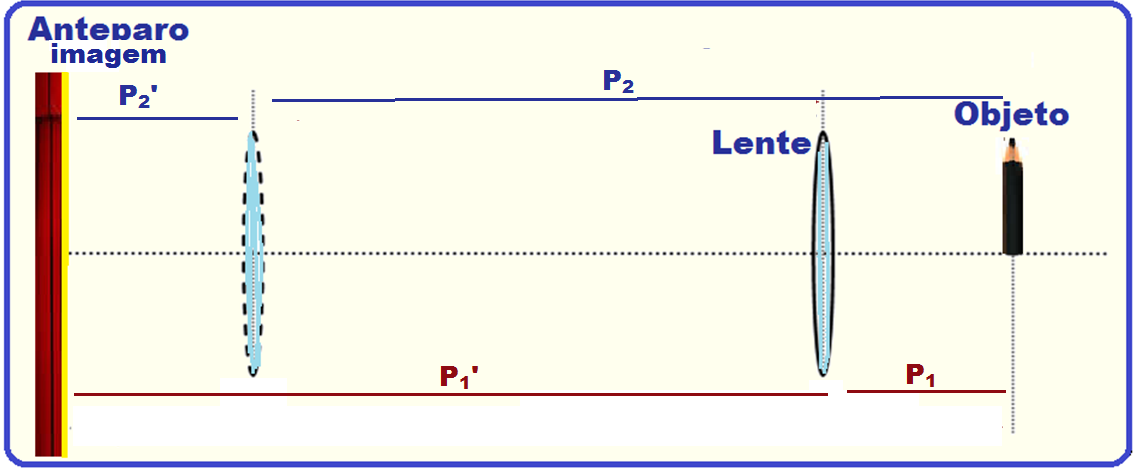
Da mesma maneira, com o objeto mais afastado da lente P2’ < P2 e │A2│< │1│(tamanho diminuído).
B) Está sendo pedida a distância entre o objeto e a lente na situação em que estão mais próximos entre si (posição P), ou seja, está pedindo P1.
Nessas condições a distância do objeto à lente será P1 e da imagem à lente P1’ = L – P1 = 10 – P1 e
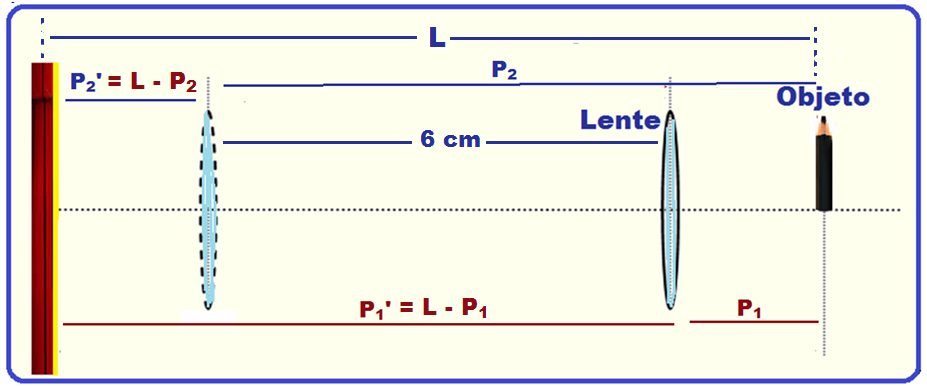
na outra posição a distância do objeto à lente será P2 e da imagem à lente P2’ = L – P2 = 10 – P2.
Observe ainda, na figura acima, que P2 – P1 = 6 (I).
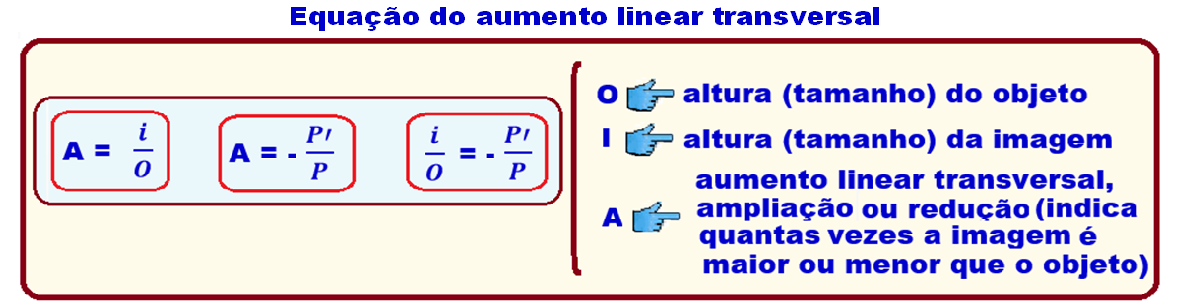
26- Primeiramente precisamos encontrar o valor da distância da imagem ao espelho, para isso vamos utilizar a equação do aumento linear:
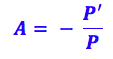
Onde:
A é o aumento linear
P’ é a distância da imagem ao espelho
P é a distância do objeto ao espelho
Isolando P’:
Substituindo, sabendo que o A foi dado no texto, quando ele diz que o aumento é de 5 vezes. Deixaremos tudo em cm, pois a resposta final está em cm:
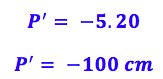
Agora que já temos a distância da imagem, podemos substituir na fórmula de gauss:
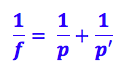
Onde:
f é a distância focal
p é a distância do objeto ao espelho
p’ é a distância da imagem ao espelho
Substituindo os valores, já jogando o sinal negativo (-100 cm) para fora da fração, ficando sinal negativo:
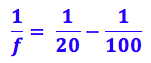
Resolvendo:
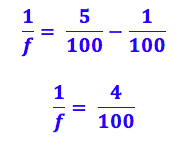
Multiplicando tudo por -1, ou seja, invertendo as frações:
R – B
27- A lupa é uma lente convergente e todos os raios de luz que incidem paralelamente ao eixo principal (caso do sol a pino) emergem da lente convergindo para o foco f. Assim, no caso do exercício, f = h.
Veja a construção geométrica da imagem em uma lupa (lente convergente) em que o objeto tem que estar entre fo = f = h e O.
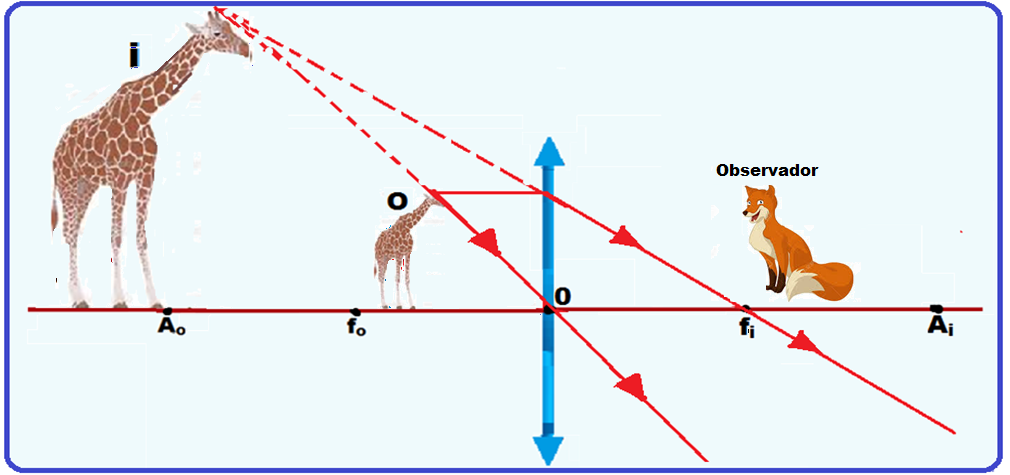
Natureza 
Virtual (obtida no cruzamento dos prolongamentos dos raios luminosos).
Localização Antes de fo
Tamanho e orientação 
maior que o objeto e direita em relação a ele.
R- D
28- Uma das imagens i do objeto que está antes do ponto antiprincipal Ao (200 cm) é formada diretamente pela lente biconvexa (convergente) que tem as seguintes características, geometricamente localizadas na figura abaixo:
Objeto O antes de Ao
Características da imagem i:
Natureza Real (obtida no cruzamento do próprio raio luminoso (linha cheia)).
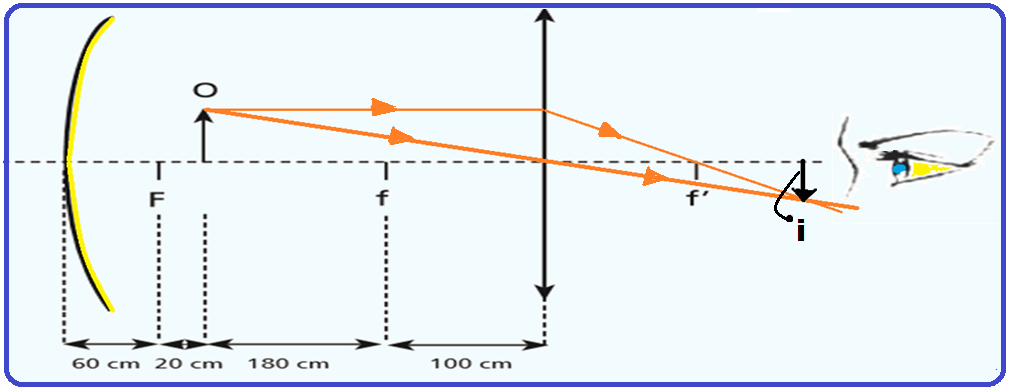
Localização entre Fi e Ai.
Tamanho e orientação menor que o objeto e invertida em relação ao mesmo.
A outra imagem i’ captada pelo espelho plano (real, invertida e maior que o objeto, pois o
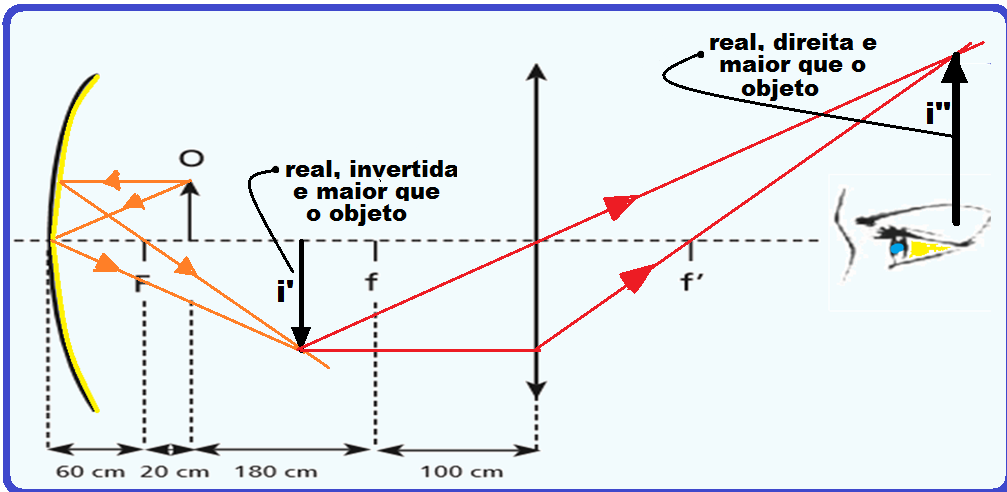
objeto está a 80cm do espelho, entre o foco F = 60cm e o centro de curvatura C = 120 cm) funciona como objeto para a lente biconvexa (convergente) e sua imagem i’’, vista pelo observador será direita em relação ao objeto, real e maior que o mesmo, conforme construção geométrica na figura acima.
R- B
29- 
Nesse microscópio de luz, a velocidade de propagação da luz é constante e vale V = c = 3.108 m/s, e assim, pela equação fundamental da ondulatória V = constante =c = λ.f, o comprimento de onda λ é inversamente proporciona à frequência f.
Como pelo enunciado, o intervalo de frequências do espectro de luz visível está compreendido entre 4,0.1014 Hz e 7,5.1014 Hz, a menor estrutura celular (menor λ) que se poderia observar nesse microscópio de luz corresponde à maior frequência nesse intervalo que é de é de f = 7,5.1014 Hz.
c = λ.f 
3.108 = λ.7,5.1014 λ = 
λ = 0,4.10-6 λ = 4.10-7 m = 400 nm.
Portanto, observando a figura você percebe que a menor estrutura celular que você pode perceber nesse microscópio é o Retículo Endoplasmático dimensão 420 nm.
R- B
30-
