Resolução comentada – Vestibulares recentes – Acústica – 2019/2019
01-
As ondas sonoras, por serem ondas de natureza mecânica, necessitam de um meio para se propagar. Além disso, essas ondas são longitudinais, ou seja, a sua direção de propagação coincide com a oscilação, portanto, mesmo em um tubo, elas não se propagam na direção transversal.
Observe a formação da onda em um tubo fechado em uma das extremidades:
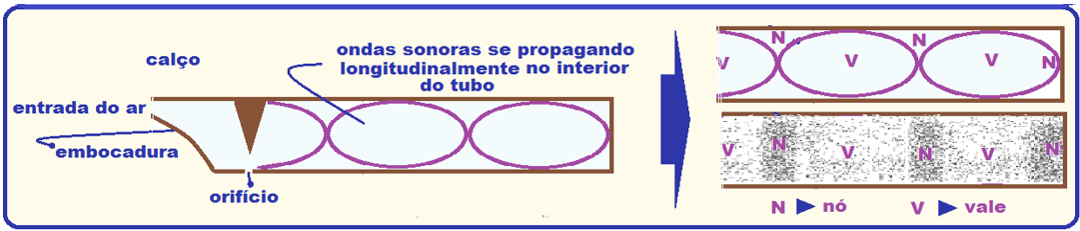
Como podemos observar pelo número de nós, quando temos esse caso a onda só consegue formar harmônicos ímpares.
Dito tudo isso, a alternativa correta é a A.
02-
Expressão matemática do nível sonoro (NS):
Como o nível sonoro foi fornecido
R- C
03-
Velocidade V de propagação da onda na corda
V = .f
R- B
04-
05-
Altura do som
A velocidade de vibração da fonte sonora (lâmina, corda, membrana, etc.) é que vai definir sua altura.
As vibrações lentas produzem sons graves (baixos e grossos) e as vibrações rápidas produzem sons agudos (altos e finos).
A altura dos sons depende também do tamanho dos corpos que vibram. Uma corda fina e curta produz sons mais agudos que os de uma corda longa e grossa.
Uma flauta pequenina de tubo bem fino também produz sons mais agudos do que um instrumento de sopro com um tubo longo e grosso como a tuba.
A altura do som está relacionada com sua frequência, ou seja, a altura (tom) é a qualidade do som que permite ao ouvido distinguir um som grave, de baixa frequência, de um som agudo, de alta frequência.
R- A
06-
Função horária da elongação
Observe que o 5 é uma constante independente das funções seno e cosseno das ondas e, como é a mesma para as duas podemos desprezá-la.
Então você terá:
R- B
07-
R- D
08-
Efeito Doppler
R- D
09-
Neste exercício, temos a ocorrência do Efeito Doppler, resumido abaixo:
Utilizando a equação de Torricelli:
10-
Trata-se do Efeito Doppler
Refere-se à variação da frequência notada por um observador quando a distância entre ele e uma fonte de ondas está aumentando ou diminuindo.
Regra de sinais
Se observador ou fonte estiverem em repouso:
R- D
11-
Efeito Doppler
Refere-se à variação da freqüência notada por um observador quando a distância entre ele e uma fonte de ondas está aumentando ou diminuindo.
Na aproximação entre fonte e observador, o mesmo perceberá o som emitido pela fonte mais agudo (maior freqüência, recebe maior número de frentes de onda na unidade de tempo) do que perceberia se fonte e observador estivessem parados.
Nesse caso, o comprimento de onda aparente percebido pelo observador será menor que o comprimento da onda emitido pela fonte (observador O1 das figuras abaixo).
No afastamento entre fonte e observador, o mesmo perceberá o som emitido pela fonte mais grave (menor freqüência, recebe menor número de frentes de onda na unidade de tempo) do que perceberia se fonte e observador estivessem parados.
Nesse caso, o comprimento de onda aparente percebido pelo observador será maior que o comprimento da onda emitido pela fonte (observador O2 das figuras acima).
Observe que o motorista da ambulância não percebe nenhuma alteração no som emitido pela sirene, pois eles se movem juntos.
R- D
12-
Efeito Doppler
R- B
13-
Primeiro devemos relembrar a fórmula do efeito Doppler para uma fonte de ondas se afastando a uma velocidade vs de um receptor que se move a uma velocidade vr, a relação entre a frequência medida pela fonte (fs) e e medida pelo receptor (fr) é dada por:
Se você não domina a teoria, ela está a seguir:
R- C
15-
R- B
16-
Comprimentos de onda e frequências para um tubo fechado
R- E
17-
I. Falsa
II. Falsa
Devem ter o mesmo comprimento de onda.
III. Verdadeira
R- C
18-
É um exercício que relaciona efeito Doppler com ondas harmônicas.
Efeito Doppler:
Para trabalharmos nos tubos sonoros precisamos encontrar a frequência aparente que chega aos tubos. Substituindo na equação acima velocidade do som V = 320 m/s; velocidade do observador (censor) Vo = 80 m/s; velocidade da fonte, nula pelo enunciado Vf = 0 e a frequência real da fonte f = 100 Hz:
Calculando
Agora que sabemos a frequência aparente podemos analisar o que ocorre com os tubos.
Primeiro vamos calcular o comprimento da onda da onda que está chegando aos tubos com frequência fa = 125 Hz e se propagando com velocidade fornecida de V = 320 m/s, utilizando a equação fundamental da ondulatória:
Isolando o comprimento de onda
Abaixo temos as expressões matemáticas dos diversos harmônicos fornecidos por tubos fechados numa extremidade:
Sendo:
R- A
19-
Veja um resumo da teoria abaixo:
Comprimentos de onda e frequências para um tubo aberto nas duas extremidades
São dados:
Comprimento do tubo (flauta)
Velocidade do som
R- C
20-
Quando o trajeto ADC é igual ao trajeto AEC (mesma diferença de caminho) capta-se um som muito intenso na saída o que indica que a interferência é construtiva e a fonte emitiu ondas em direções opostas mas em concordância de fase.
Quando se aumentou gradativamente o trajeto ADC até que fique como mostrado na figura a intensidade do som na saída fica praticamente nula e aí você tem a primeira interferência destrutiva.
Na situação da figura fornecida observe que o trecho AD é 10 cm maior que o trecho AE e que o trecho DC é 10 cm maior que o trecho EC, o que implica que o caminho que a onda percorre no trajeto ACD é 20 cm maior que o caminho que a onda percorre no trajeto AEC.
Isso significa que a diferença de caminho entre uma interferência construtiva e a destrutiva sucessiva é de d2 – d1 = 20 cm = 0,2 m.
Como na saída o som é praticamente nulo, aí você tem interferência destrutiva, cuja teoria está a seguir:
O primeiro mínimo corresponde a n = 0
Utilizando a equação fundamental da ondulatória com a velocidade do som no interior do tubo V = 320 m/s = 0,4 m
R- C