Resolução comentada – Vestibulares recentes – Acústica – 2019/2019

01-

As ondas sonoras, por serem ondas de natureza mecânica, necessitam de um meio para se propagar. Além disso, essas ondas são longitudinais, ou seja, a sua direção de propagação coincide com a oscilação, portanto, mesmo em um tubo, elas não se propagam na direção transversal.

Observe a formação da onda em um tubo fechado em uma das extremidades:

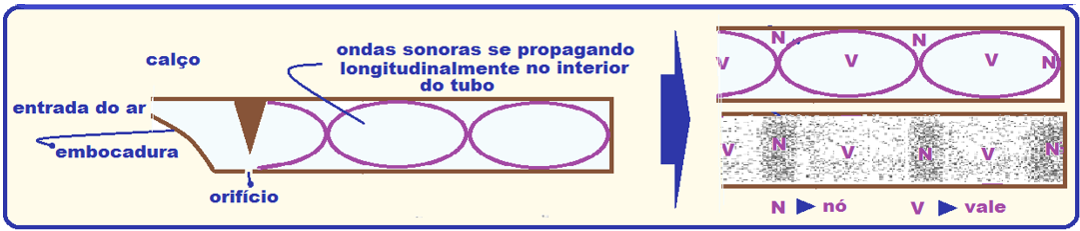
Como podemos observar pelo número de nós, quando temos esse caso a onda só consegue formar harmônicos ímpares.

Dito tudo isso, a alternativa correta é a A.

02-

Expressão matemática do nível sonoro (NS):

Como o nível sonoro foi fornecido = 60 dB, você pode descobrir a intensidade do som I recebida pelo ouvido da pessoa sendo dado Io = 10-12 W/m2:

R- C

03-

Velocidade V de propagação da onda na corda

V = .f 340 = 10.f f = 340/19 f = 34 Hz.

R- B

04-

R- C

05-

Altura do som

A velocidade de vibração da fonte sonora (lâmina, corda, membrana, etc.) é que vai definir sua altura.

As vibrações lentas produzem sons graves (baixos e grossos) e as vibrações rápidas produzem sons agudos (altos e finos).

A altura dos sons depende também do tamanho dos corpos que vibram. Uma corda fina e curta produz sons mais agudos que os de uma corda longa e grossa.

Uma flauta pequenina de tubo bem fino também produz sons mais agudos do que um instrumento de sopro com um tubo longo e grosso como a tuba.

A altura do som está relacionada com sua frequência, ou seja, a altura (tom) é a qualidade do som que permite ao ouvido distinguir um som grave, de baixa frequência, de um som agudo, de alta frequência.

R- A

06-

Função horária da elongação

Observe que o 5 é uma constante independente das funções seno e cosseno das ondas e, como é a mesma para as duas podemos desprezá-la.

Então você terá:

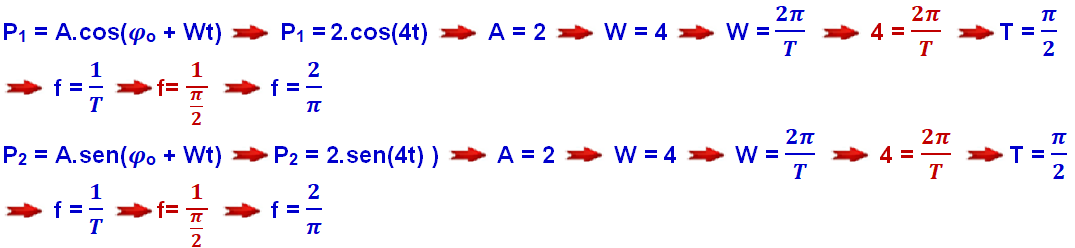
R- B

07-

R- D

08-

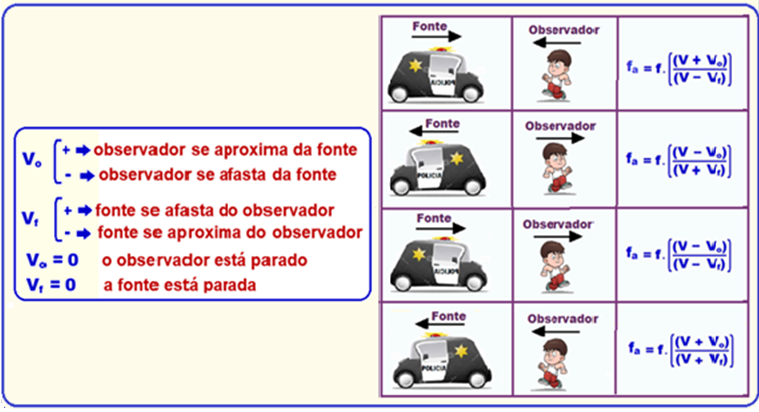
Efeito Doppler

R- D

09-

Neste exercício, temos a ocorrência do Efeito Doppler, resumido abaixo:

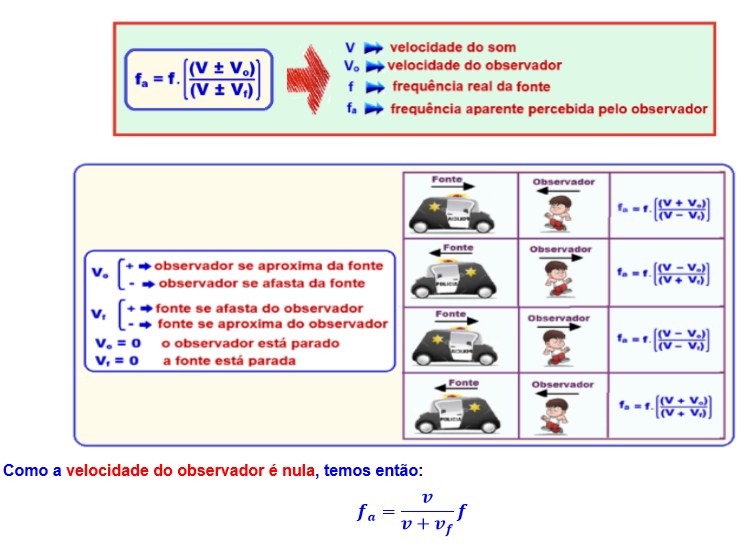
Utilizando a equação de Torricelli:

10-

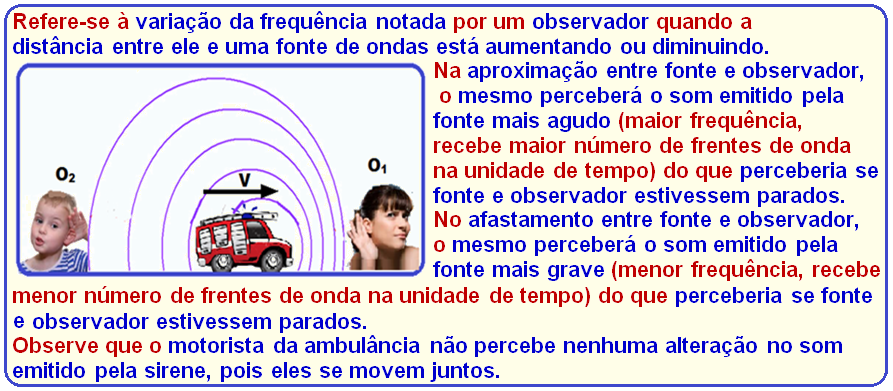
Trata-se do Efeito Doppler

Refere-se à variação da frequência notada por um observador quando a distância entre ele e uma fonte de ondas está aumentando ou diminuindo.

Regra de sinais

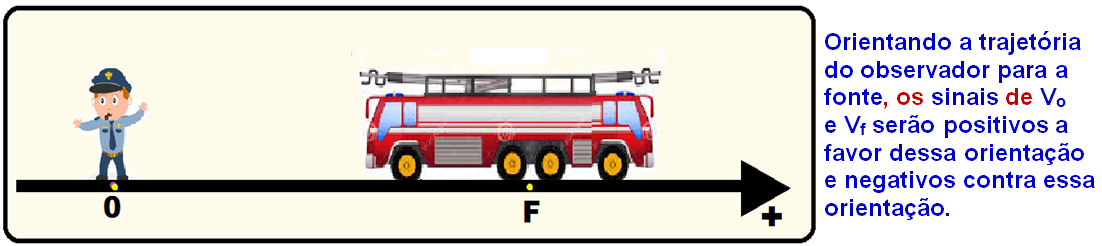
Se observador ou fonte estiverem em repouso:

R- D

11-

Efeito Doppler

Refere-se à variação da freqüência notada por um observador quando a distância entre ele e uma fonte de ondas está aumentando ou diminuindo.

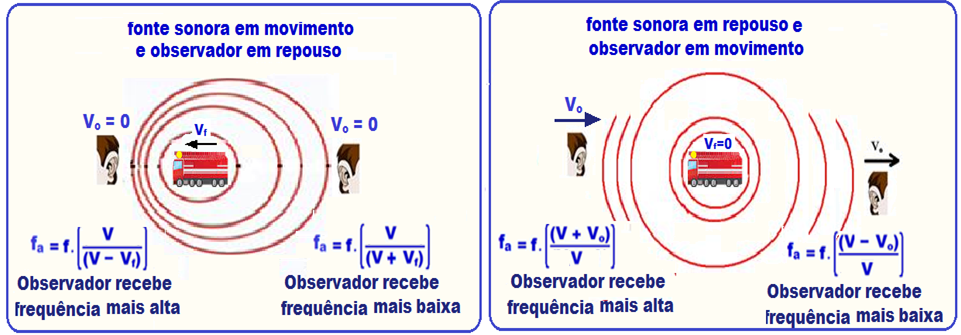
Na aproximação entre fonte e observador, o mesmo perceberá o som emitido pela fonte mais agudo (maior freqüência, recebe maior número de frentes de onda na unidade de tempo) do que perceberia se fonte e observador estivessem parados.

Nesse caso, o comprimento de onda aparente percebido pelo observador será menor que o comprimento da onda emitido pela fonte (observador O1 das figuras abaixo).

No afastamento entre fonte e observador, o mesmo perceberá o som emitido pela fonte mais grave (menor freqüência, recebe menor número de frentes de onda na unidade de tempo) do que perceberia se fonte e observador estivessem parados.

Nesse caso, o comprimento de onda aparente percebido pelo observador será maior que o comprimento da onda emitido pela fonte (observador O2 das figuras acima).

Observe que o motorista da ambulância não percebe nenhuma alteração no som emitido pela sirene, pois eles se movem juntos.

R- D

12-

Efeito Doppler

R- B

13-

Primeiro devemos relembrar a fórmula do efeito Doppler para uma fonte de ondas se afastando a uma velocidade vs de um receptor que se move a uma velocidade vr, a relação entre a frequência medida pela fonte (fs) e e medida pelo receptor (fr) é dada por:

14-

Se você não domina a teoria, ela está a seguir:

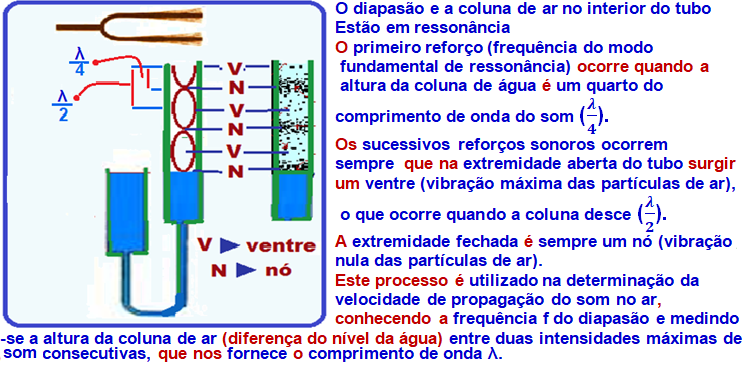
R- C

15-

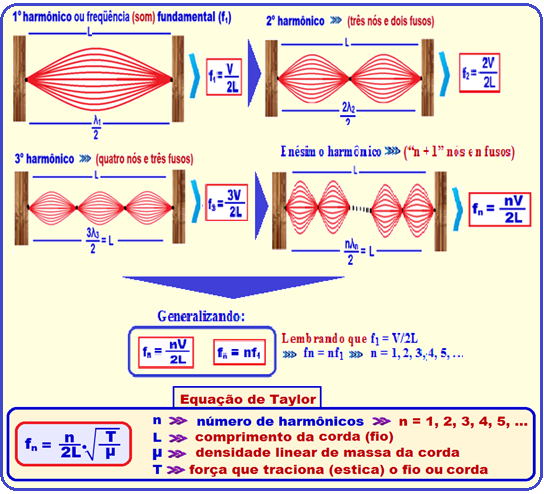
R- B

16-

Comprimentos de onda e frequências para um tubo fechado

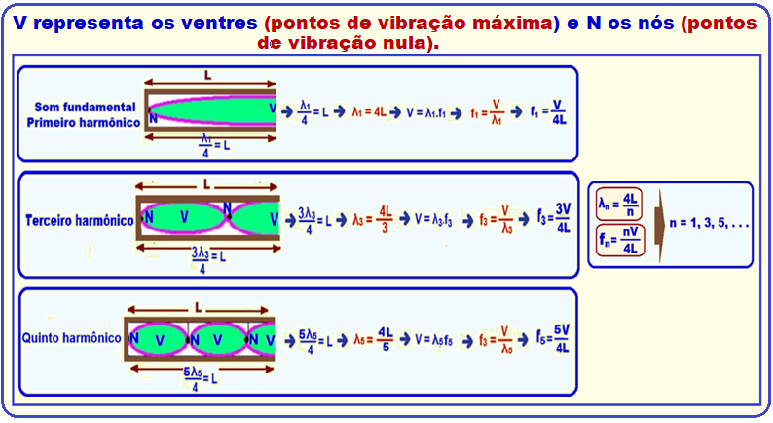
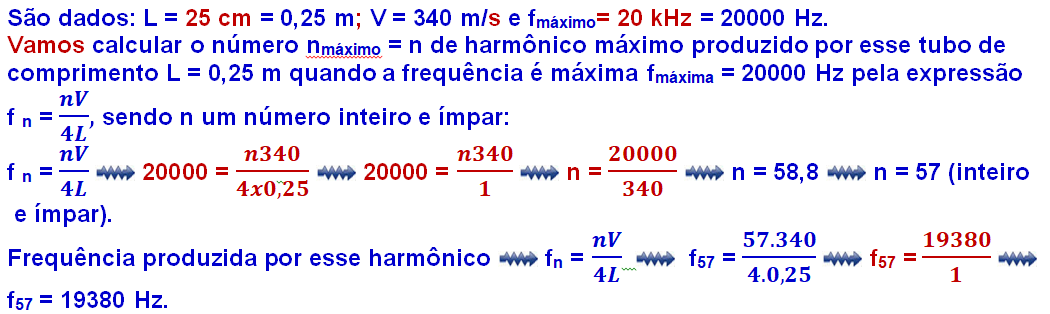
R- E

17-

I. Falsa a velocidade da luz (e de outra qualquer onda eletromagnética) no vácuo é constante e vale V = c = 3.108 m/s, independente da frequência.

II. Falsa

Devem ter o mesmo comprimento de onda.

III. Verdadeira

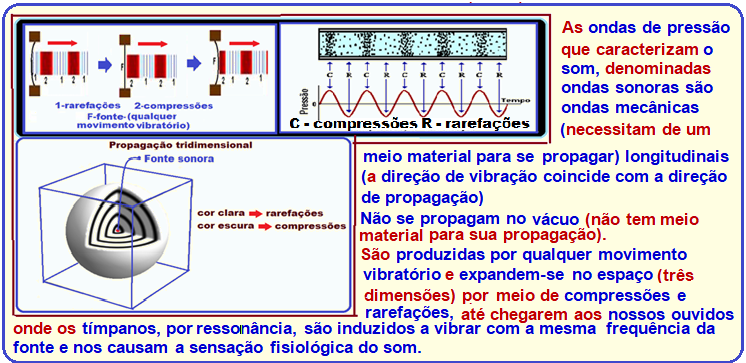
R- C

18-

É um exercício que relaciona efeito Doppler com ondas harmônicas.

Efeito Doppler:

Para trabalharmos nos tubos sonoros precisamos encontrar a frequência aparente que chega aos tubos. Substituindo na equação acima velocidade do som V = 320 m/s; velocidade do observador (censor) Vo = 80 m/s; velocidade da fonte, nula pelo enunciado Vf = 0 e a frequência real da fonte f = 100 Hz:

Calculando fa = 100x(400/320) = 400×1,25 fa = 125 Hz (frequência aparente, recebida pelos tubos).

Agora que sabemos a frequência aparente podemos analisar o que ocorre com os tubos.

Primeiro vamos calcular o comprimento da onda da onda que está chegando aos tubos com frequência fa = 125 Hz e se propagando com velocidade fornecida de V = 320 m/s, utilizando a equação fundamental da ondulatória:

Isolando o comprimento de onda = = = m. (comprimento de onda das ondas que chegam aos tubos sonoros)

Abaixo temos as expressões matemáticas dos diversos harmônicos fornecidos por tubos fechados numa extremidade:

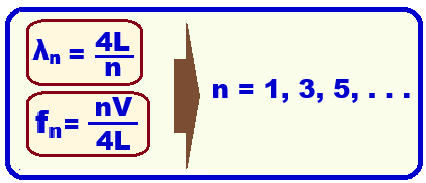
Sendo: o comprimento de onda dos n harmônicos; L o comprimento de cada tubo; n o número de harmônicos; fn a frequência de n harmônicos e V a velocidade da onda

Como se trata de tubos fechados, os mesmos só possuem harmônicos ímpares com n = 1, 3 e 5.

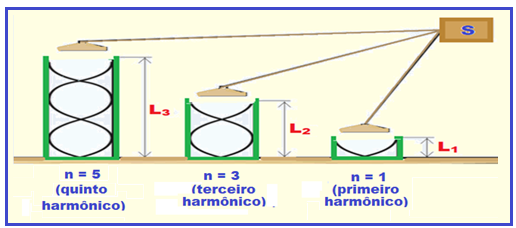
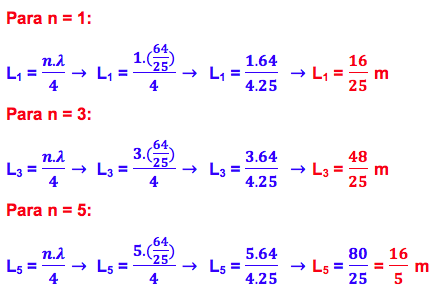
R- A

19-

Veja um resumo da teoria abaixo:

Comprimentos de onda e frequências para um tubo aberto nas duas extremidades

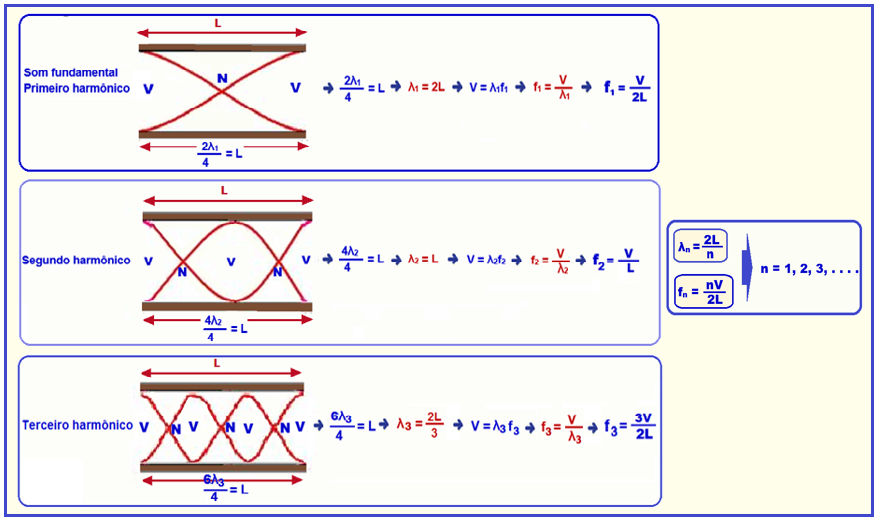
São dados:

Comprimento do tubo (flauta) L = 34 cm = 0,34 m

Velocidade do som Vs = 340 m/s

R- C

20-

Quando o trajeto ADC é igual ao trajeto AEC (mesma diferença de caminho) capta-se um som muito intenso na saída o que indica que a interferência é construtiva e a fonte emitiu ondas em direções opostas mas em concordância de fase.

Quando se aumentou gradativamente o trajeto ADC até que fique como mostrado na figura a intensidade do som na saída fica praticamente nula e aí você tem a primeira interferência destrutiva.

Na situação da figura fornecida observe que o trecho AD é 10 cm maior que o trecho AE e que o trecho DC é 10 cm maior que o trecho EC, o que implica que o caminho que a onda percorre no trajeto ACD é 20 cm maior que o caminho que a onda percorre no trajeto AEC.

Isso significa que a diferença de caminho entre uma interferência construtiva e a destrutiva sucessiva é de d2 – d1 = 20 cm = 0,2 m.

Como na saída o som é praticamente nulo, aí você tem interferência destrutiva, cuja teoria está a seguir:

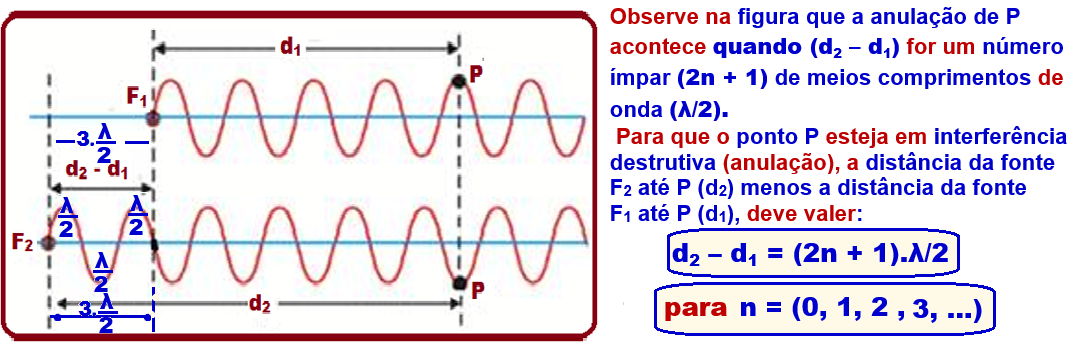
O primeiro mínimo corresponde a n = 0 d2 – d1 = (2n +1). 0,2 = (2.0 + 1). 0,2 = 1.
= 0,4 m.

Utilizando a equação fundamental da ondulatória com a velocidade do som no interior do tubo V = 320 m/s = 0,4 m V = .f 320 = 0,4.f f = f = 800 Hz.

R- C