Hidrostática – 2020
MECÂNICA – Vestibulares recentes – 2020
DINÂMICA
Hidrostática
01- (FGV – SP – Economia – 2020)

Um barquinho de brinquedo, contendo no seu interior uma bolinha de gude de massa m, flutua na água de um recipiente, graduado em unidades de volume.
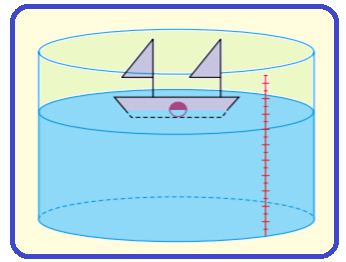
Sendo a densidade da água igual a ![]() e a densidade da bolinha igual a
e a densidade da bolinha igual a ![]() , se a bolinha for retirada do barquinho, a escala do recipiente indicará uma diminuição de volume igual a
, se a bolinha for retirada do barquinho, a escala do recipiente indicará uma diminuição de volume igual a
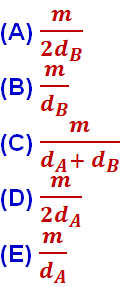
Enunciado do princípio de Arquimedes

Expressão matemática do Empuxo

Com a bolinha de massa m e o barco de massa mb, em equilíbrio você terá:


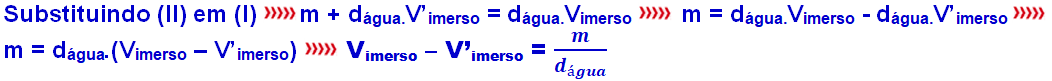
R- E
02- (FPS-Faculdade Pernambucana de Saúde-PE-2020)

Determine, aproximadamente, a altura da atmosfera da Terra, medida a partir do nível do mar.

Se você não domina a teoria, ela está a seguir:
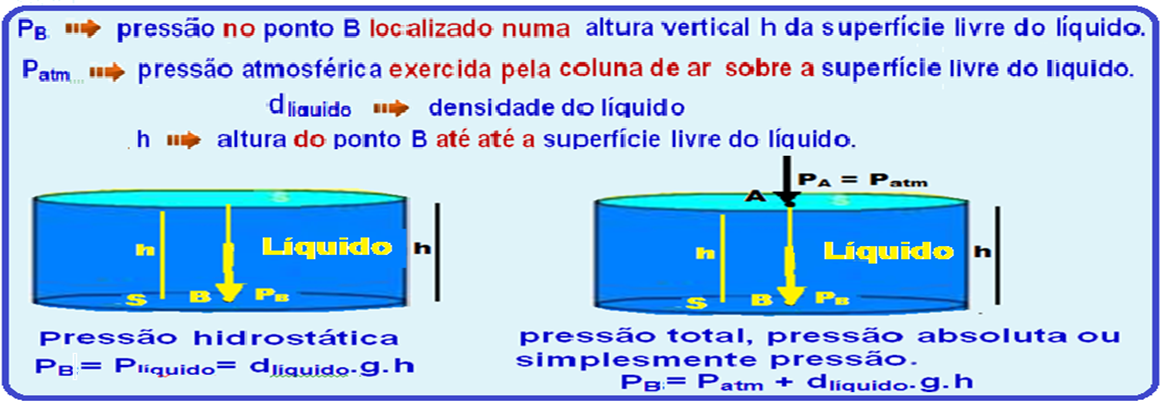
Teorema Fundamental da Hidrostática ou Teorema de Stevin



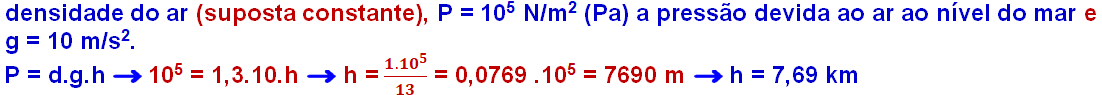
R- C
03- (ACAFE – Associação Catarinense das Fundações Educacionais –Medicina – 2020).

A reciclagem é uma atividade importante para a sustentabilidade do planeta.
Ela pode ocorrer tanto com a matéria prima que constitui um determinado objeto, como com o próprio objeto que pode ser reutilizado para desempenhar novamente sua função ou criar outros objetos.
Pensando nesta reciclagem, surfistas criaram, a partir de garrafas PET de 2 litros, uma prancha de Stand Up com 93 dessas garrafas, como mostra a figura abaixo.

Neste sentido, considere uma surfista que deseja testar a flutuabilidade dessa prancha.
Para isso, ela fica de pé sobre a prancha em uma piscina e percebe que ela flutua bem. Desconsiderando o peso das garrafas e sabendo que elas ficaram com 1/3 de seu volume submerso, marque a alternativa que indica, em kg, a massa da surfista. Dados: densidade da água 103 kg/m3 e g = 10 m/s2.
![]()
Enunciado do princípio de Arquimedes

Expressão matemática do Empuxo


R- D
04- (AFA-2020)

Um pequeno tubo de ensaio, de massa 50 g, no formato de um cilindro, é usado como ludião – uma espécie de submarino miniatura, que desce, verticalmente, dentro de uma garrafa cheia de água.
A figura 1, a seguir, ilustra uma montagem, onde o tubo, preenchido parcialmente de água, é mergulhado numa garrafa pet, completamente cheia de água.
O tubo fica com sua extremidade aberta voltada para baixo e uma bolha de ar, de massa desprezível, é aprisionada dentro do tubo, formando com ele o sistema chamado ludião.
A garrafa é hermeticamente fechada e o ludião tem sua extremidade superior fechada e encostada na tampa da garrafa.
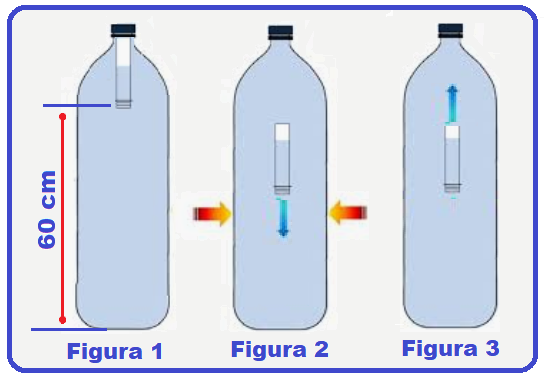
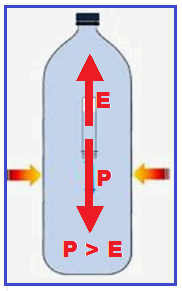
Uma pessoa, ao aplicar, com a mão, uma pressão constante sobre a garrafa faz com que entre um pouco mais de água no ludião, comprimindo a bolha de ar. Nessa Condição, o ludião desce, conforme a figura 2, a partir do repouso, com aceleração constante, percorrendo 60 cm, até chegar ao fundo da garrafa, em 1,0 s.
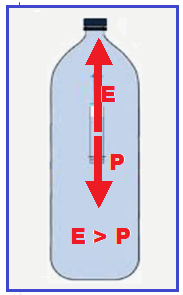
Após chegar ao fundo, estando o ludião em repouso, a pessoa deixa de pressionar a garrafa. A bolha expande e o ludião sobe, conforme figura 3, percorrendo os 60 cm em 0,5 s.
Despreze o atrito viscoso sobre o ludião e considere que, ao longo da descida e da subida, o volume da bolha permaneça constante e igual a ![]() e V, respectivamente.
e V, respectivamente.
Nessas condições, a variação de volume, ΔV = V- ![]() , em cm³, é igual a
, em cm³, é igual a
![]()





R- A
05- (CEDERJ – RJ – meio do ano – 019/029)

Um cubo de gelo encontra-se em repouso flutuando na água. Considere que P e E representam,

respectivamente, os módulos do peso do cubo de gelo e do empuxo que a água exerce sobre o gelo. F denomina o módulo da resultante das forças que atuam no cubo de gelo. Então:
(A) F = (E + P) > 0
(B) F= P; E = 0
(C) F = 0; E = P
(D) F < P < E
Teorema de Arquimedes – Empuxo
Enunciado do princípio de Arquimedes

Expressão matemática do Empuxo


R- C
06- (IFTO – Instituto Federal de Educação, Ciência e Tecnologia do Tocantins – 2020)

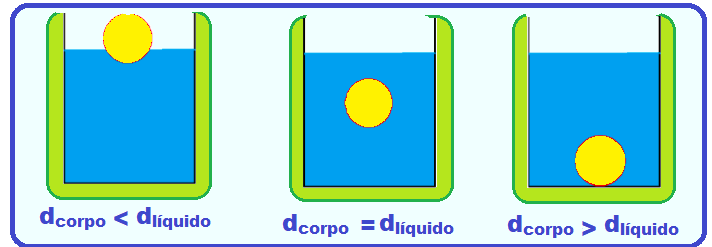
Quando colocamos na água duas pedras de gelo, uma pequena e outra grande, ambas flutuam; em contrapartida, quando colocamos na água dois objetos de aço maciço de tamanhos distintos, ambos afundam.

A propriedade física que está vinculada a esse fato é:
a) a massa.
b) a densidade.
c) o peso.
d) a aceleração.
e) a energia potencial.
O gelo é menos denso (mais leve) que a água e, por isso, independente de seu volume flutua.
O objeto de aço é mais denso (mais pesado) que a água e, por isso, independente de seu volume afunda.
R- B
07- (Insper – SP – 2020)

 .
.

Enunciado do princípio de Arquimedes

Expressão matemática do Empuxo

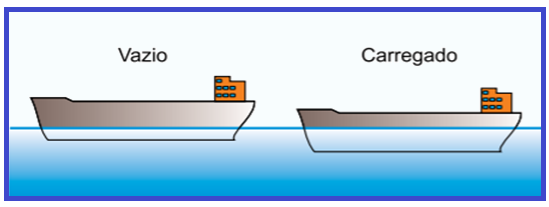
Navio Vazio

Navio com grãos

 R- A
R- A
08- (Universidade Estadual de Ponta Grossa – UEPG – PR – 2020)

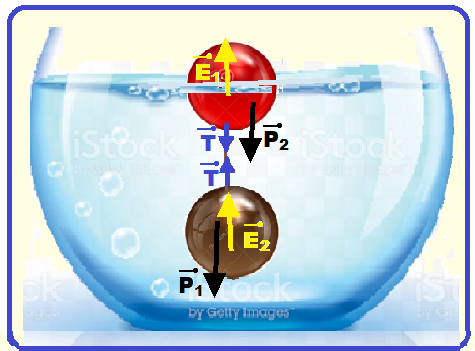
Duas esferas estão unidas por um fio ideal, inextensível, de massa e volume desprezíveis.
As esferas são colocadas num reservatório com água de modo que, na situação de equilíbrio, uma das esferas (esfera 1) fica flutuando com metade de seu volume submerso, a outra esfera (esfera 2) fica totalmente submersa e o fio, que une as duas, está orientado na direção perpendicular à superfície da água.

Sabendo que o volume de cada uma das esferas é 100 cm3 e que a massa da esfera 1 é 30 g e a da esfera 2 é 120 g, assinale o que for correto.
01) Se o fio que une as duas esferas for cortado, na condição de equilíbrio, as duas esferas irão flutuar com 1/3 de seus volumes submersos.
02) A densidade absoluta da esfera 2 é 4 vezes maior do que a da esfera 1.
04) A pressão hidrostática exercida pelo líquido sobre a esfera 1 é menor do que a pressão hidrostática exercida sobre a esfera 2.
08) A tensão no fio é 0,4 N.
16) O empuxo exercido pelo líquido sobre a esfera 1 é 0,5 N.
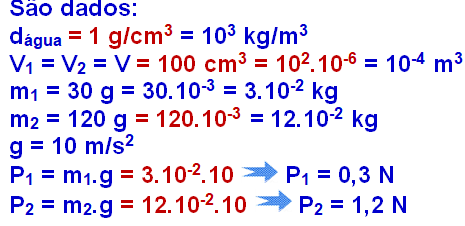
Forças que agem sobre cada esfera:

01. Falsa


2. Correta
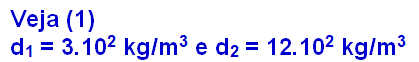
04 .Correta

8. Falsa
![]()
16. Correta
![]()
R- (02 + 04 + 16) = 22
09- (PUCPR – MEDICINA – 2020)

Alguns mamíferos adaptados à vida marinha, como o elefante-marinho e a foca, possuem

características fisiológicas que permitem a eles mergulhar a grandes profundidades, prendendo a respiração por vários minutos.
Num experimento científico, um pequeno sensor de pressão foi preso ao corpo de um elefante-marinho e, durante um mergulho em busca de alimento, foi registrada a pressão hidrostática (pH) a que o animal ficou submetido, em função do tempo de mergulho (t).
De posse dos dados, os cientistas construíram o gráfico mostrado a seguir.
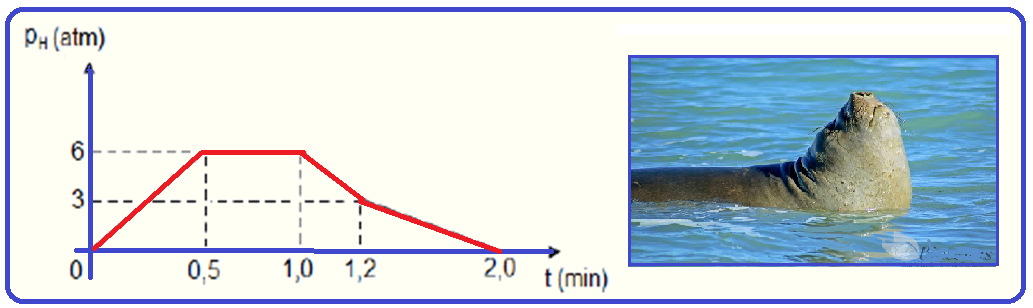
![]()
A) a componente vertical da velocidade do elefante-marinho, desde a superfície até atingir a profundidade máxima, foi constante e igual a 2 m/s.
B) a trajetória do elefante-marinho durante todo o seu mergulho foi retilínea.
C) a profundidade máxima atingida pelo animal em seu mergulho foi de 30 m.
D) a área do gráfico ![]() é numericamente igual ao deslocamento total do elefante-marinho em seu mergulho.
é numericamente igual ao deslocamento total do elefante-marinho em seu mergulho.
E) entre os instantes t = 0,5 min e t = 1,0 min, o elefante-marinho permaneceu em repouso.

R- A
10- (PUC – Rio – 2020)

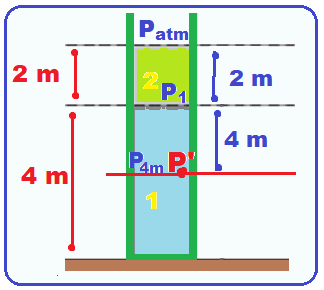
Sejam dois fluidos distintos cujas densidades são 1,00 g/cm3 e 0,80 g/cm3, colocados em um tubo vertical, como mostrado na figura. O tubo está aberto à atmosfera. Sejam ![]()
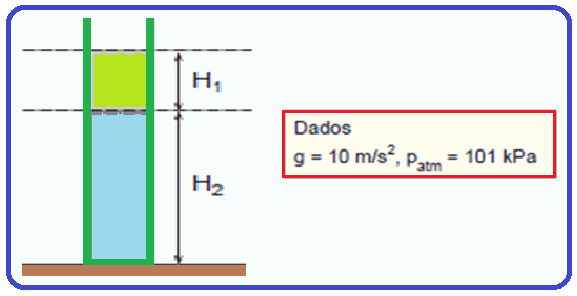
Encontre a pressão absoluta, em kPa, dentro do tubo, a uma altura de 4,0 m em relação ao fundo do tubo.
(A) 56
(B) 101
(C) 153
(D) 157
(E) 187


R- D
11- ESCOLA NAVAL – CPAEN – 22019/2020

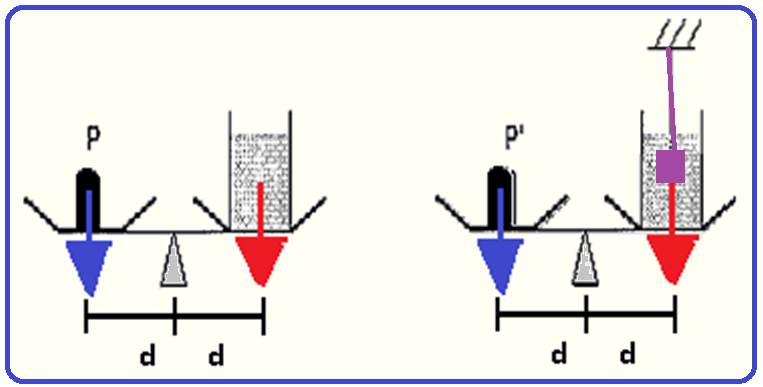
Observe as figuras abaixo.
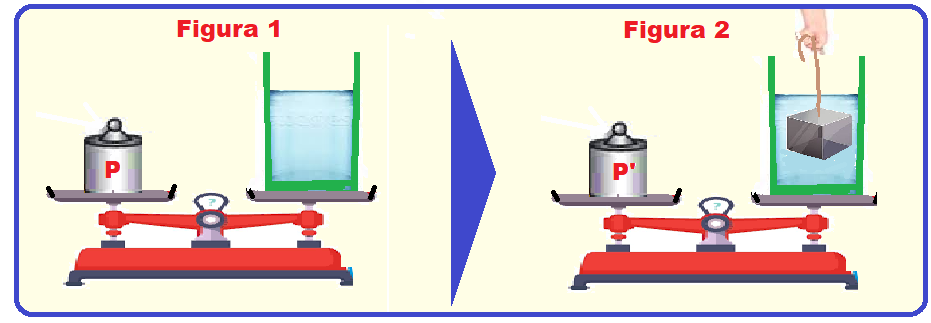
As figuras mostram uma balança de dois pratos em dois instantes diferentes. A figura 1 mostra um recipiente cheio de água, de densidade 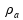 , equilibrado por um peso P. Na figura 2, um cubo de aresta a e densidade
, equilibrado por um peso P. Na figura 2, um cubo de aresta a e densidade 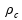 pendurado num fio, é mergulhado inteiramente na água do mesmo recipiente sem tocar seu fundo. Que massa foi adicionada ao prato da balança (figura 2) para que o equilíbrio fosse restabelecido?
pendurado num fio, é mergulhado inteiramente na água do mesmo recipiente sem tocar seu fundo. Que massa foi adicionada ao prato da balança (figura 2) para que o equilíbrio fosse restabelecido?
12- Universidade Estadual de Maringá (UEM) – PR – 2020

-
Considere fluidos incompressíveis, não viscosos e em regime estacionário. Assinale o que for
-
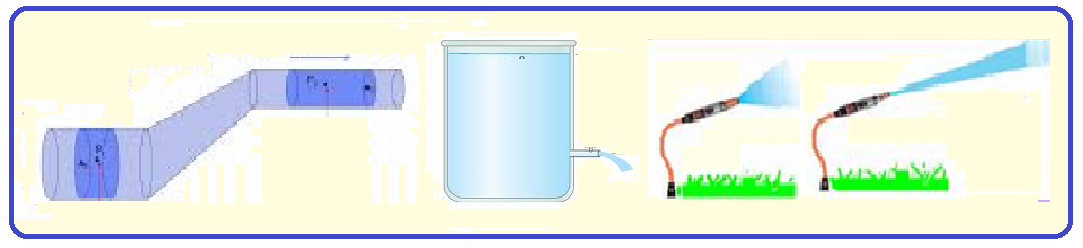
-
correto.
-
01) A velocidade de um fluido em um tubo de diâmetro variável é menor na região de menor área de seção transversal.
-
02) A pressão de um fluido em um tubo horizontal de diâmetro variável é maior na região de maior velocidade.
-
04) A pressão de um fluido em movimento em um tubo de diâmetro constante é menor na região de maior altura.
-
08) A movimentação ascendente ou descendente de submarinos submersos no mar pode ser explicada pela equação de Bernoulli.
-
16) A elevação de um automóvel sobre um dos pistões de uma prensa hidráulica pode ser explicada pelo princípio de Pascal.
– Vamos avaliar cada uma das afirmativas com breves revisões dos conceitos envolvidos.
-
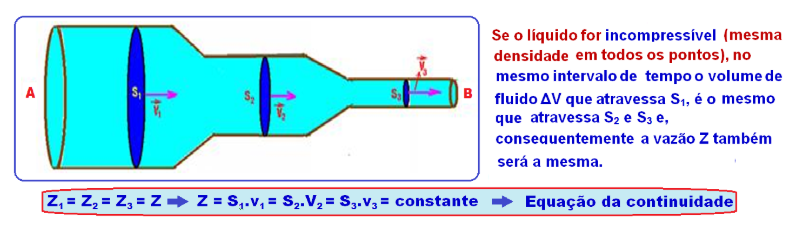
A velocidade de um fluido em um tubo de diâmetro variável é menor na região de menor área de seção transversal.
-
A pressão de um fluido em um tubo horizontal de diâmetro variável é maior na região de maior velocidade.
Pela mesma argumentação do ítem anterior, esta alternativa está correta.
-
A pressão de um fluido em movimento em um tubo de diâmetro constante é menor na região de maior altura.

-
A movimentação ascendente ou descendente de submarinos submersos no mar pode ser explicada pela equação de Bernoulli.
A movimentação ascendente ou descendente de um submarino pode ser explicada pelo princípio de Arquimedes, que é um caso especial da equação de Bernoulli quando 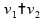 .
.
-
A elevação de um automóvel sobre um dos pistões de uma prensa hidráulica pode ser explicada pelo princípio de Pascal.
O princípio de Pascal enuncia que: “O acréscimo de pressão exercido num ponto de um líquido ideal em equilíbrio é transmitido integralmente (ou seja, sem redução) a todos os pontos desse líquido e também às paredes do recipiente onde está contido”.
Para um elevador hidráulico, vale a situação descrita abaixo:
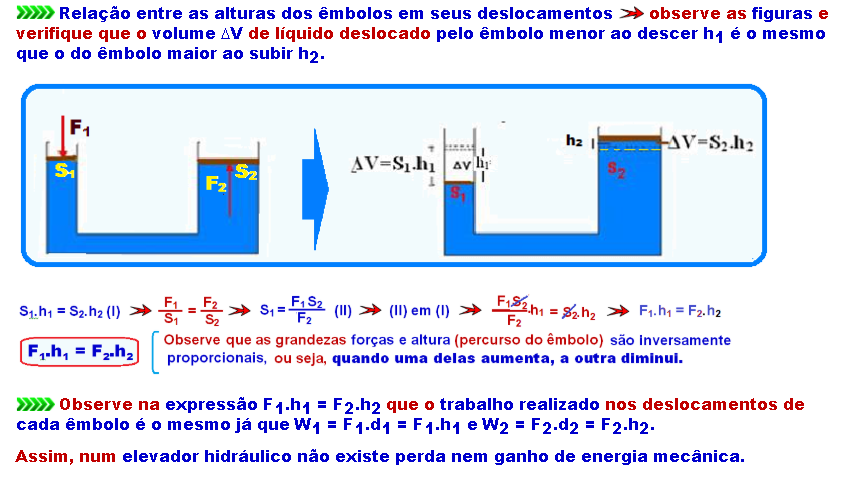
A pressão comunicada do ponto 1 é transmitida ao ponto 2 integralmente quando temos um fluído ideal, da mesma maneira como é enunciado o princípio de Pascal.
Portanto, esta alternativa é verdadeira.
As alternativas corretas são 02), 08) e 16).
13- Faculdade de Ciências Médicas da Santa Casa de São Paulo – SP – 2020)

![]()
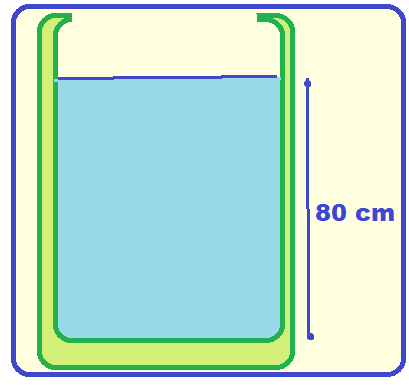
![]()
a) Calcule a pressão exercida apenas pela massa de água e a pressão total sobre o fundo do recipiente, em pascals.
b) Adiciona-se na água certa quantidade de álcool e agita-se a mistura até que fique homogênea.
Em seguida, uma esfera de massa 3,0 kg e volume ![]() é inserida no recipiente que contém a mistura dos dois líquidos e fica totalmente submersa, sob a ação de uma força de empuxo igual a 19 N.
é inserida no recipiente que contém a mistura dos dois líquidos e fica totalmente submersa, sob a ação de uma força de empuxo igual a 19 N.
Calcule as densidades, em ![]() , da esfera e da mistura.
, da esfera e da mistura.
a)
Teorema Fundamental da Hidrostática ou Teorema de Stevin



b)

Para o cálculo da densidade da mistura (álcool + água) você pode utilizar o teorema do empuxo de Arquimedes:
Enunciado do princípio de Arquimedes

Expressão matemática do Empuxo


14- (Faculdade de Tecnologia Termomecânica – SP- meio do ano – 019/020)

O gráfico mostra como varia a pressão num líquido X (linha vermelha) e na água (linha azul), ambos
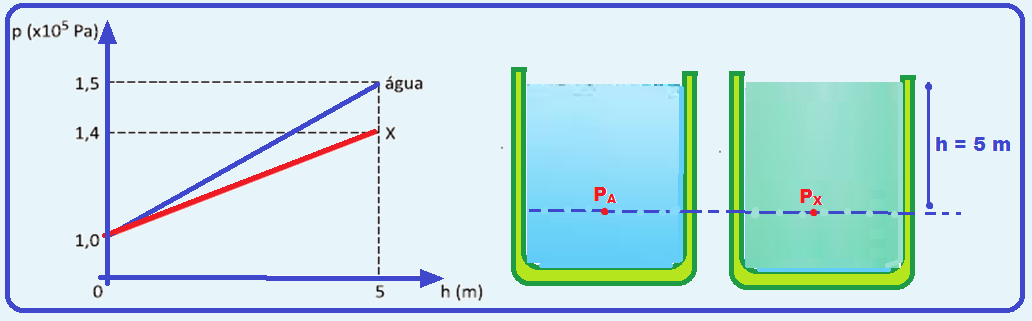
em equilíbrio e em função da profundidade, a partir de sua superfície livre.
É correto afirmar que a densidade do líquido X, relativamente à da água, é igual a
(A) 0,4. (B) 0,5. (C) 0,6. (D) 0,8. (E) 0,9
Gráfico do Teorema de Stevin

Água ![]() PA = Patm + dA.g.h
PA = Patm + dA.g.h ![]() 1,5.105 = 1.105 + dA.10.5
1,5.105 = 1.105 + dA.10.5 ![]() dA = 0,5.105/50 = 50.103/50
dA = 0,5.105/50 = 50.103/50 ![]()
dA = 103 kg/m3.
Líquido ![]() PL = Patm + dL.g.h
PL = Patm + dL.g.h ![]() 1,4.105 = 1.105 + dL.10.5
1,4.105 = 1.105 + dL.10.5 ![]() dL = 0,4.105/50 = 40.103/50
dL = 0,4.105/50 = 40.103/50 ![]()
dL = 0,8.103 kg/m3.
dL/dA = 0,8.103/1.103 ![]() dL/dA = 0,8.
dL/dA = 0,8.
R- D
15- (UEA – AM – 2020)

Dois paralelepípedos, A e B, de densidades ![]() , estão totalmente imersos, em equilíbrio, em água.
, estão totalmente imersos, em equilíbrio, em água.
O paralelepípedo A está preso pelo fio 1 a uma haste fixa, fora da água.
O paralelepípedo B está preso pelo fio 2, fixado no fundo do recipiente.
O volume do paralelepípedo B é o dobro do volume do paralelepípedo A e as densidades (d) dos paralelepípedos A, B e da água satisfazem a relação ![]() .
.
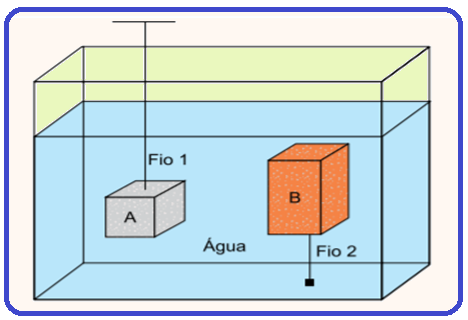
Sendo ![]() os módulos dos empuxos exercidos pela água, respectivamente, nos paralelepípedos A e B, temos que
os módulos dos empuxos exercidos pela água, respectivamente, nos paralelepípedos A e B, temos que

Empuxo de Arquimedes


R- E
16- (UECE – Universidade Estadual do Ceará – 2020)

Considere um navio petroleiro parado em alto mar.

Desprezando os movimentos de ondas e forças de arrasto do vento, caso o navio esteja em equilíbrio estático, é correto afirmar que é
A) nula a soma vetorial da força peso com a força de empuxo.
B) vertical para cima o vetor força resultante da soma da força peso e da força de empuxo.
C) vertical para baixo o vetor força resultante da soma da força peso e da força de empuxo.
D) horizontal o vetor força de empuxo e se anula com a força de atrito viscosa da água.
Veja figuras abaixo:
Se o petróleo flutua é porque ele é menos denso que a água do mar e, assim ele estaria sempre flutuando.
R- A
17- (UECE – Universidade Estadual do Ceará – 2020)

Nos últimos meses, foram noticiadas muitas queimadas na Floresta Amazônica.

Considerando que não haja correntes de vento horizontais na região de incêndio, a fumaça tende a subir, pelo fato de
A) ter menor densidade que o ar acima do incêndio.
B) ter maior densidade que o ar acima do incêndio.
C) ter menor viscosidade que o ar nas regiões laterais à queimada.
D) ter maior viscosidade que o ar nas regiões laterais à queimada.
Menos denso menos pesado sobe e mais denso mais pesado desce.
R- A
18- (UEG – GO – MEDICINA – 2020)

A figura a seguir apresenta dois vasos que estão em equilíbrio hidrostático, devido às pressões
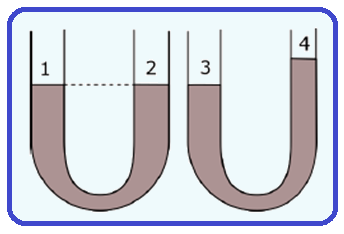
exercidas na superfície dos líquidos 1, 2, 3 e 4.
Os vasos são preenchidos com líquido de mesma densidade, logo, na superfície desses líquidos a pressão
Teorema Fundamental da Hidrostática ou Teorema de Stevin

Todos os pontos da mesma altura suportam a mesma pressão (figura abaixo).
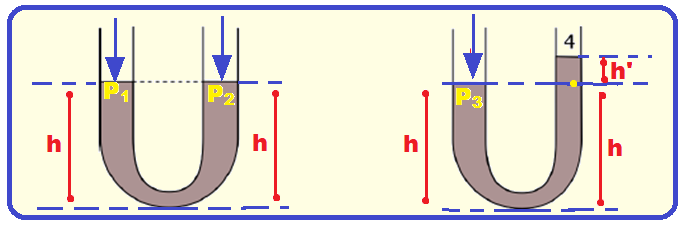
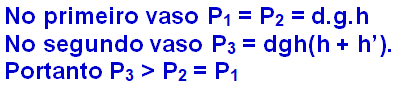
R- E
19- (Universidade Estadual de Ciências da Saúde de Alagoas – UNCISAL – 2020)

Para decidir qual a melhor caixa d’água a ser instalada em uma obra, o responsável utilizou o modelo a seguir, com o objetivo de avaliar a pressão exercida pela caixa na laje e a pressão exercida pela água em um ponto no fundo de cada caixa.
A figura seguinte mostra as caixas d’água I, II e III, de formatos distintos, apoiadas sobre lajes.
As caixas estão fechadas, cheias de água, seus volumes são, respectivamente, 2V, 2V e V, e suas áreas de base (contato) com a laje são, respectivamente, 2A, A e A.
Na figura, estão mostradas as alturas das caixas d’água.
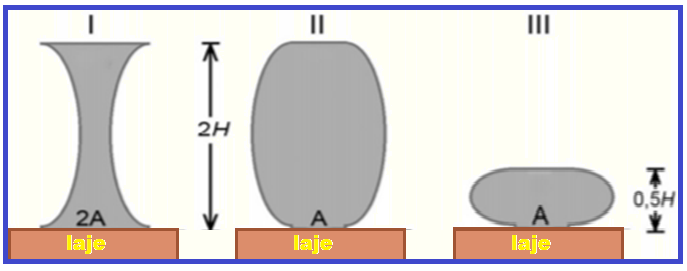
Desconsiderando-se a pressão atmosférica e o peso do material de que são feitas as caixas d’água, qual é a classificação, em ordem crescente, da razão entre a pressão que a caixa d’água exerce sobre a laje e a pressão da água em um ponto na base da caixa?
![]()


R- A

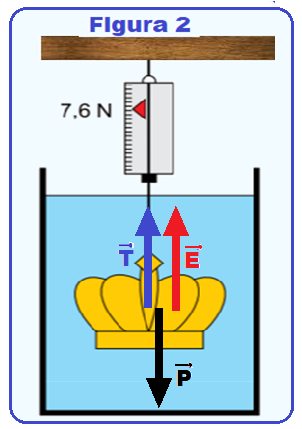
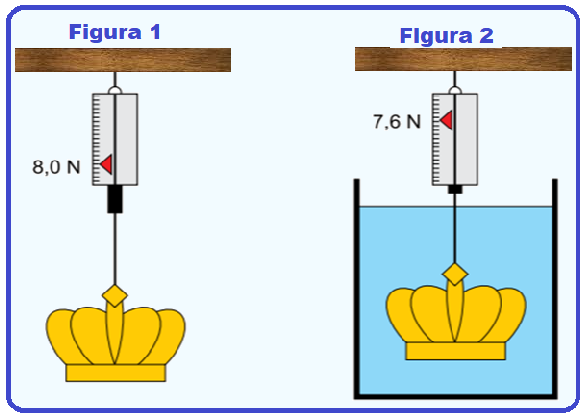
Para determinar a densidade de uma coroa metálica maciça, foi realizado um experimento em que ela foi pendurada em um dinamômetro ideal por dois modos diferentes: um no ar e outro totalmente imersa na água em equilíbrio contida em um recipiente, de acordo com as figuras 1 e 2, respectivamente.

a) Cálculo da massa da coroa utilizando a figura 1.
No ar, a intensidade da força de tração T no fio do dinamômetro (indicação do dinamômetro, T = 8,0 N
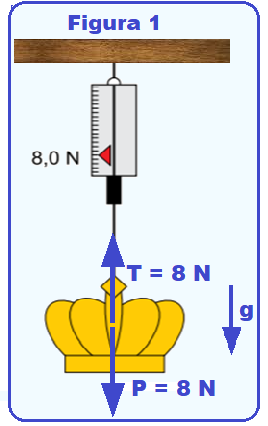
é o próprio peso da coroa ![]() T = P
T = P ![]() 8 = m.g
8 = m.g ![]() 8 = m.10
8 = m.10 ![]() m = 0,8 kg (massa da coroa).
m = 0,8 kg (massa da coroa).
Na figura 2 surge o empuxo de Arquimedes fornecido por:
Expressão matemática do Empuxo

Assim, as forças que surgem sobre a coroa totalmente imersa na água (figura 2) são: