Resolução – Hidrostática – 2018/2019
Hidrostática – 2018/2019
01-
R- E
02-
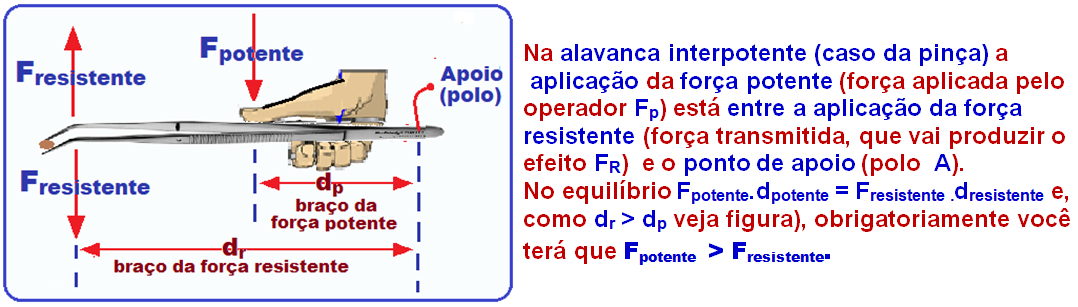
R- A
03-
Em primeiro lugar, deve-se encontrar a relação entre as densidades do objeto e da água utilizando a fórmula para a força de empuxo E realizada em um corpo com um volume submerso Vs no fluído de densidade ρ, sendo esse empuxo calculado como
Como o corpo de densidade ρo e volume total Vo está em equilíbrio, a força de empuxo sobre o corpo será igual a força peso, utilizando ρa para denotar a densidade da água e usando que o volume de água deslocado pelo fluído Vs é 3/5 do volume do objeto Vo (60%), temos:
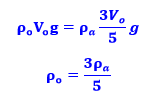
04-
Empuxo
R- C
05-
06-
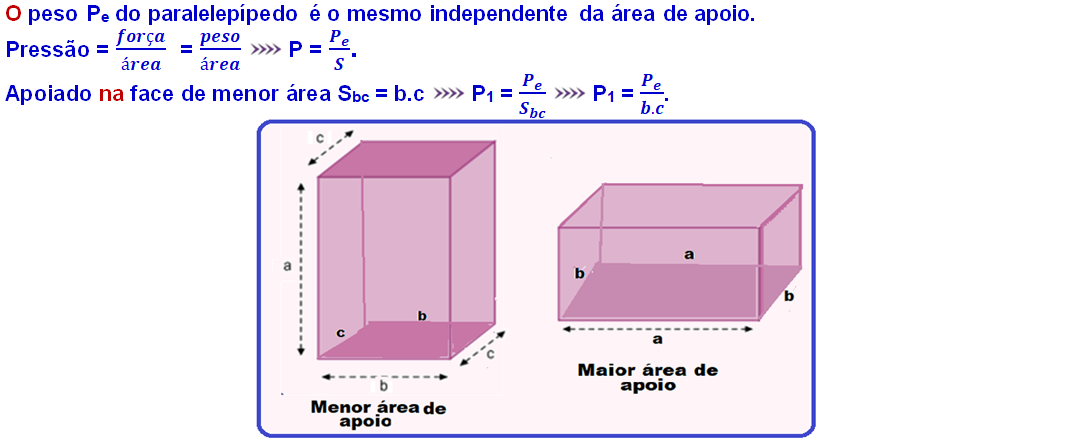
a) A partir da definição de pressão, podemos escrever:
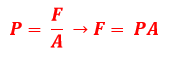
Sendo que a área A é a que está sujeita a força aplicada F. Repare que a força a qual a superfície está sujeita é a do peso do bloquinho:
No entanto, a massa do bloco não varia, logo, a força é constante para qualquer posicionamento do bloquinho, portanto:
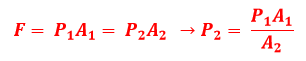
Sendo e as áreas de contato da primeira e da segunda configuração, respectivamente. As áreas de contato têm a forma de retângulos, fazendo com que seus valores sejam o produto simples de uma dimensão pela outra. Substituindo os valores, obtemos:
b) Nesta situação, teremos três forças atuando no bloquinho, a força peso, a força normal à superfície e a força de empuxo exercida pelo fluído e contrária à força peso. O esboço abaixo retrata as três forças atuantes.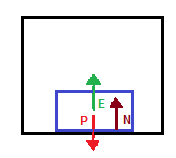
Aplicando a segunda lei de Newton e considerando que as forças que apontam para cima possuem sinal negativo, teremos:
Porém, o bloquinho encontra-se parado, logo possui aceleração nula, logo:
A força peso é o produto da massa do objeto pela aceleração gravitacional:
A força de empuxo é dada por:
Em que V é o volume de líquido deslocado, é a densidade do líquido e g é a aceleração gravitacional. Pelo princípio de Arquimedes, o volume de líquido deslocado é igual ao volume do objeto submerso no líquido.
Usando as equações e o princípio de Arquimedes, obtemos:
A massa do bloquinho pode ser obtida utilizando o conceito de pressão apresentado no item a, utilizando a pressão e a área da primeira configuração, tal que:
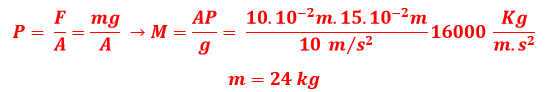
Substituindo na equação da força normal:
07-
Para este exercício, vamos utilizar o Teorema Fundamental da Hidrostática, que se encontra resumido abaixo:
A situação descrita no enunciado encontra-se esboçada abaixo:
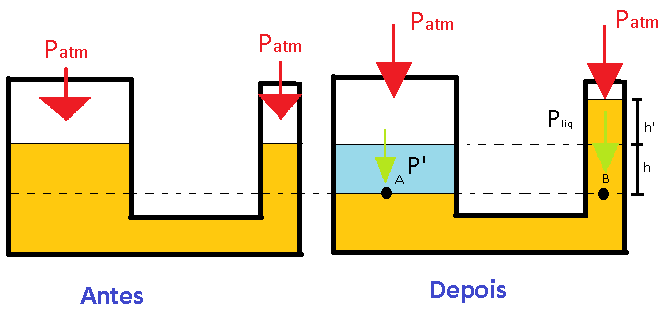
08-
Vcasca = Vcaroço = V
dcasca = mcasca/V 
0,4 = mcasca/V mcasca = 0,4V
dcaroço = mcaroço/V dcaroço = mcaroço/V mcaroço = dcaroço.V
dcorpo = mcorpo/Vcorpo dcorpo = (mcasca + mcaroço)/2V dcorpo = (0,4V + dcaroço.V)/2V
R- C
09-
Se você não domina a teoria, ela está a seguir:
Enunciado do princípio de Arquimedes
Expressão matemática do Empuxo
Expressão matemática do peso (força vertical e para baixo)
Veja figura abaixo:
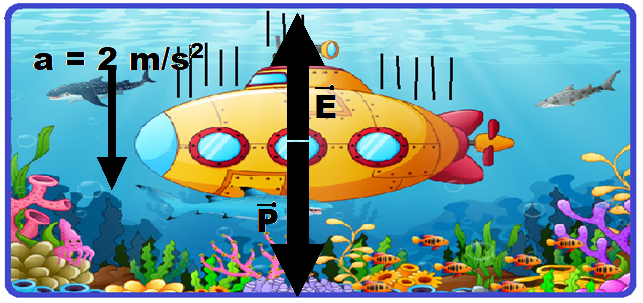
R- C
10-
R- C
11-
Se você não domina a teoria, ela está a seguir.
R- E
12-
No caso do exercício você terá Pfundo = 11 000/10 + 1 atm = 1 101 atm.
R- D
13-
Teorema Fundamental da Hidrostática ou Teorema de Stevin
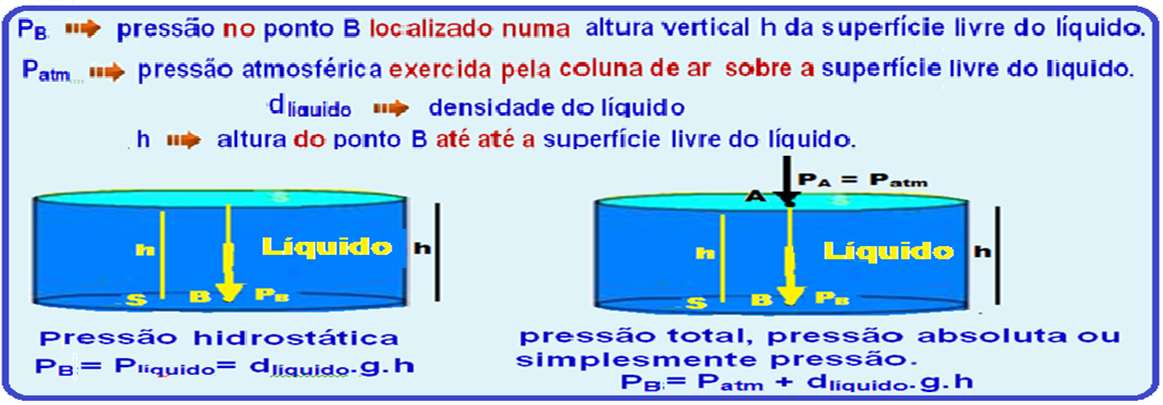
Observe pelo teorema de Stevin que quanto maior a altura h da coluna líquida (no caso do fundo do aquário), maior será a pressão devido a água nesse ponto.
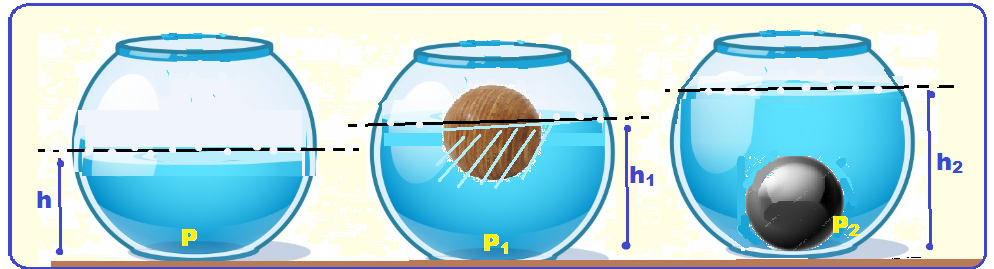
Assim, h2 > h1 > h (veja figuras acima)
R- B
14-
Resumo teórico
Colocando as forças que agem sobre o balão:
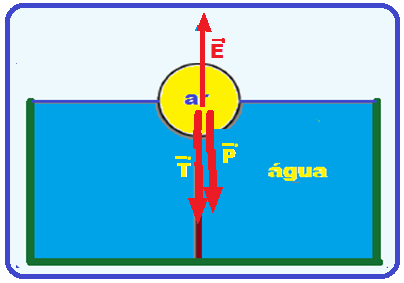
R- E
15-
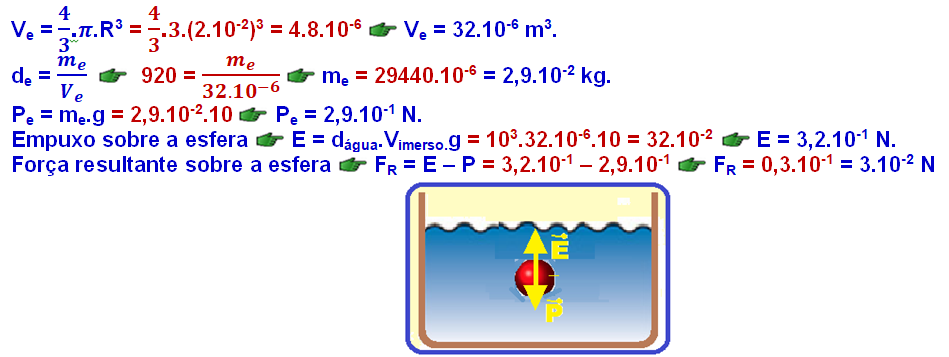
R- A
16-
01. Falso – como todas as melancias tem densidade menor que a da água todas devem flutuar (mais denso, mais pesado em baixo e menos denso menos pesado, em cima).
02. Falso – dependendo da altura que são soltas algumas podem ficar submersas, mas, no equilíbrio final todas ficam flutuando (veja 01).
04. Falso – A força peso, vertical e para baixo é constante, mas a força de empuxo vertical e para cima (peso do volume de líquido deslocado) vai aumentando à medida que a melancia vai entrando na água.
Assim, durante a entrada na água a força resultante (FR= P- E) vai diminuindo até que quando P = E ela fica nula. Portanto a velocidade da melancia durante a penetração na água vai diminuindo.
08- Correto – veja 04.
16- Falso – a força resultante só é nula quando a melancia retorna e fica flutuando o que só ocorre quando P = E.
R – 08
17-
Enunciado do princípio de Arquimedes
Se o corpo estiver parcialmente imerso
No caso do exercício são dados: densidade do bloco de madeira dcorpo = 680 kg/m3; volume da parte imersa Vimersa = 2×0,6×0,25 = 0,3 m3; densidade da água dágua = 1,0.103 kg/m3 e volume total = volume do corpo (imerso) + volume da cabeça (emerso) = 0,3 m3 + Vcabeça.
R- C
18-
Veja a teoria a seguir:
Sem alternativa – questão anulada.
19-
R- D
20-
Trata-se do Empuxo de Arquimedes – corpo parcialmente imerso
R- B
21-
22-
Enquanto o gelo não se transformar totalmente em água (fusão do gelo) a temperatura do sistema permanece constante (0oC).
A massa de gelo que se transforma em água é a mesma e, como a densidade da água é maior que a do gelo (gelo menos denso “mais leve” flutua na água) um volume de mesma massa de água é menor que o de mesma massa de gelo, pois a expressão d
, mostra que sendo m constante, densidade e volume são inversamente proporcionais (Vágua < Vgelo).
À medida que o gelo vai derretendo o volume de água líquida Vágua do sistema vai aumentando e o respectivo volume de gelo que era essa água (Vgelo) diminuindo, o que provoca uma diminuição do volume total do sistema, pois Vàgua < Vgelo).
R- B
23-
a)
Definição do Princípio Fundamental da Dinâmica ou Segunda lei de Newton
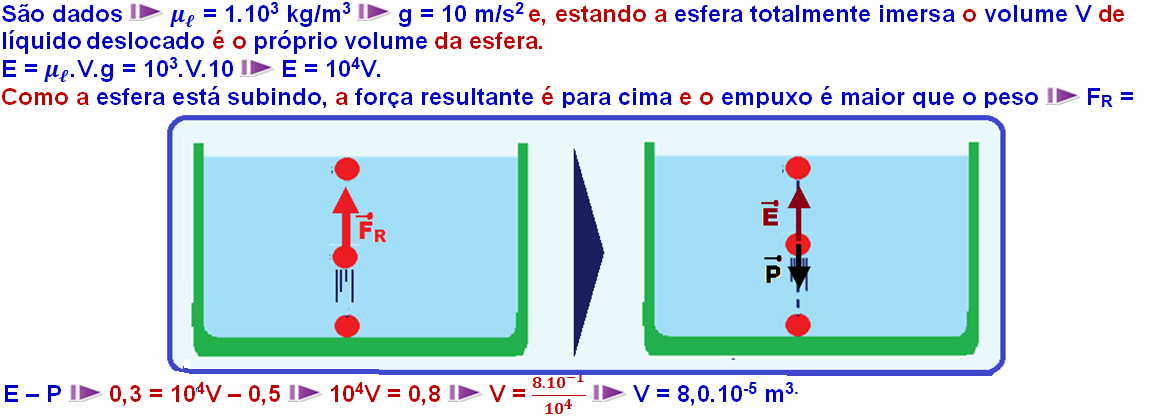
Aplicando a segunda lei de Newton ( FR = m.a), vamos calcular a aceleração a de subida da esfera sendo:
b)
Forças que agem sobre a esfera:
Peso, vertical e para baixo de intensidade 
P = m.g = 0,05.10 P = 0,5 N.
Empuxo de Arquimedes força vertical e para cima fornecida por:
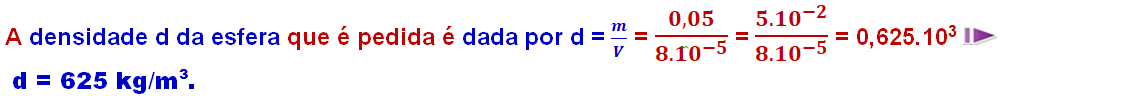
24-
Pelo gráfico, quando o cilindro está totalmente emerso (no ar) a força de tração é constante e vale T = 120 N, que é o próprio peso do cilindro 
P = 120 N.
O gráfico também informa que, quando o cilindro está totalmente imerso na água a força de tração vale T = 40 N e nesse caso, além do peso P = 120 N (vertical e para baixo) você tem o empuxo E (vertical e para cima).
Intensidade do empuxo
25-
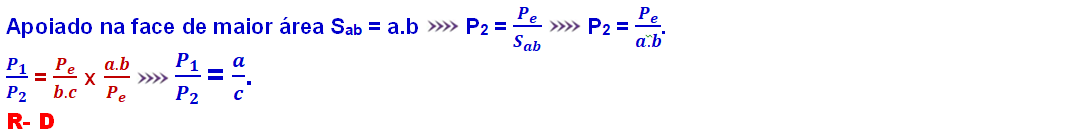
26-
