Resolução comentada HIDROSTÁTICA – 2017 – 2016 e 2015
Resolução comentada
HIDROSTÁTICA – 2017 – 2016 e 2015
Densidade e Pressão
01- Para essa questão apenas utilizaremos a fórmula da pressão:
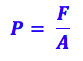
Onde:
P é a pressão
F é a força exercida
A é a área aonde essa força foi exercida
Bom, como foi dito no próprio exercício essa pressão se deve ao peso da coluna de ar, então podemos substituir essa força por m.g:
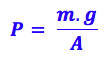Isolando a massa:
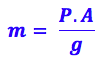Colocando os valores:
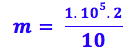m = 2.104 Kg
R – C
02-
01) Pressão é uma grandeza vetorial, portanto tem módulo, direção e sentido definidos
01. Falsa 
Se a força 
estiver inclinada de um ângulo β em relação à horizontal, a parcela dessa
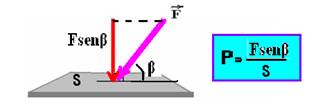
força que exerce a pressão é a componente vertical de 
, ou seja, é Fsenβ, conforme a figura acima.
A pressão sempre vai estar relacionada ao módulo da força que age perpendicularmente à superfície. Então, não importa a direção que a força é aplicada, ela não muda a direção da pressão, que é sempre perpendicular a superfície.
Só o que leva em conta na pressão, portanto, é a intensidade.
02) A diferença de pressão entre dois pontos no interior de um líquido homogêneo e em equilíbrio é
proporcional à diferença de profundidade entre esses dois pontos.
02. Correta Teorema de Stevin Observe a figura abaixo onde, quem varia é apenas a pressão vertical, onde o líquido que é homogêneo e incompressível está em equilíbrio.
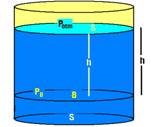
Na superfície livre superior (A) desse líquido age a pressão atmosférica (Patm), exercida pela coluna de ar que está sobre ele. Num ponto qualquer B do interior do líquido, a pressão (PB) que age é a soma da pressão atmosférica com a pressão exercida pela coluna líquida acima dele, devido à seu peso.
PB=Patm + Plíquido — PB=Patm + F/S — PB= Patm + peso do líquido/S — PB=Patm + (mlíquido.g)/S — dlíquido=mlíquido/Vlíquido — dlíquido=mlíquido/S.h — mlíquido=dlíquido.S.h — PB=Patm + (dlíquido.S.h)/S — PB=Patm+ dlíquido.g.h — esta expressão é chamada de Teorema Fundamental da Hidrostática ou de Teorema de Stevin
04) No sistema internacional de medidas (SI) a unidade de pressão é o Pascal (Pa).
04. Correta Pa = N/m2.
08) Quando um dado ponto de um líquido em equilíbrio no interior de um recipiente sofre uma variação de pressão, essa variação de pressão é transmitida a todos os pontos do líquido e das paredes do recipiente.
08. Correta Considere um fluido (líquidos e gases que fluem para as regiões inferiores de um recipiente até preenchê-los totalmente) emequilíbrio (vertical e horizontal) no interior de um recipiente.
Esse líquido exerce sobre as paredes do recipiente que o contem forças que se tornam de maior intensidade à medida que a profundidade aumenta.
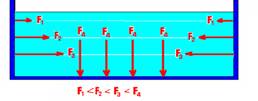
Observe que as forças, na mesma horizontal, em ambos os extremos, tem a mesma intensidade, pois o líquido está em equilíbrio horizontal, caso contrário, ele se moveria nessa direção.
16) Estando um líquido em um recipiente aberto, a pressão na superfície do líquido é nula.
16. Falsa veja 02.
R- (02 + 04 + 08) = 14
03- F = ? 
S = 1,0 mm2 = 1,0.10-6 m2 a pressão sistólica (sangue) de valor Ps = 1,0.105.160 = 160.105 Pa (N/m2) que é a pressão exercida por uma coluna de h = 160 mm = 0,16 m de mercúrio, de valor PHg = d.g.h = 13,6.103.10.16.10-2 = 217,6.102 PHg = 21760 Pa (N/m2).
É essa pressão (21760 Pa) devido à coluna de Hg (mecânica) que age sobre a área S = 1,0.
10-6 m2, devido à força de intensidade F tal que P = 
21760 = 
F = 2,176.
10-2 N.
Teorema de Stevin – pressão hidrostática – vasos comunicantes
04- Devido ao teorema de Stevin, P=dlíquido.g.h, para um mesmo líquido, quanto maior a profundidade, maior será a pressão. Observe na figura abaixo, onde a esfera está imersa, que
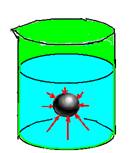
as forças exercidas pelo líquido sobre ela são maiores nas áreas inferiores (onde h é maior) que nas superiores (onde hé menor). A força resultante de todas essas forças está dirigida para cima, e corresponde ao empuxo que age sobre essa esfera. Nas laterais essas forças se anulam,
R- E
05- a) Se o processo ocorre à temperatura constante trata-se de uma transformação isotérmica e, aplicando a equação dos gases ideais 
Po.Vo/To = P.V/T Po.Vo = P.V volume inicial de ar no tubo cilíndrico de área da base S Vo volume final de ar no tubo cilíndrico V =(4/5)Vo Po = 1 atm Po.Vo = P.V 1.Vo = P.(4/5)Vo P = 5/4 P = 1,25 atm.
Mas, uma das consequências do princípio de Stevin é que todos os pontos do mesmo nível horizontal suportam a mesma pressão PM = PN 1,35.105 = 105 + 104 H 1,35.105 – 1,0.105 = 104 H H = 0,35.105 /104 H = 0,35.10 H = 3,5m
06-
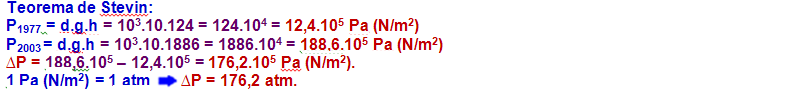
07- A pressão total no fundo do lago devido apenas à agua vale P = 5 atm – 1 atm = 4 atm.
Como para cada 1 atm de pressão a altura equivale a 10m, o lago terá h = 4×10 = 40 m de profundidade.
R- A
Experiência de Torricelli
08- a) Se o processo ocorre à temperatura constante trata-se de uma transformação isotérmica e, aplicando a equação dos gases ideais Po.Vo/To = P.V/T Po.Vo = P.V volume inicial de ar no tubo cilíndrico de área da base S Vo volume final de ar no tubo cilíndrico V =(4/5)Vo Po = 1 atm Po.Vo = P.V 1.Vo = P.(4/5)Vo P = 5/4 P = 1,25 atm.
Mas, uma das consequências do princípio de Stevin é que todos os pontos do mesmo nível horizontal suportam a mesma pressão PM = PN 1,35.105 = 105 + 104 H 1,35.105 – 1,0.105 = 104 H H = 0,35.105 /104 H = 0,35.10 H = 3,5m
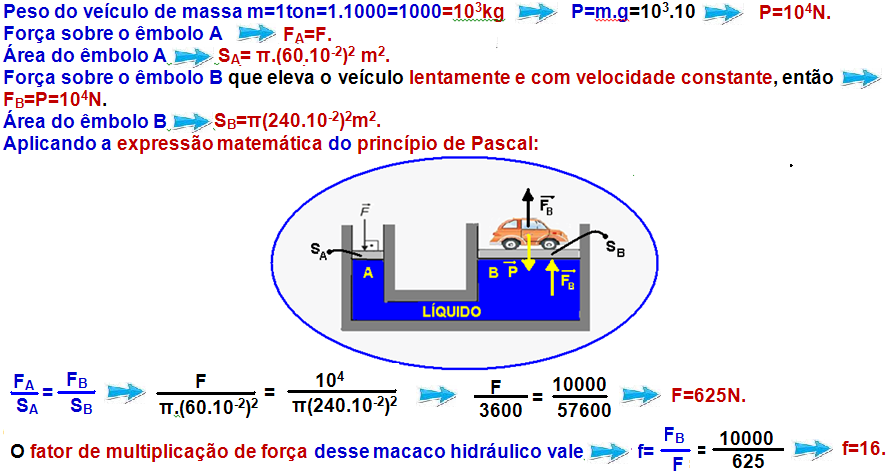
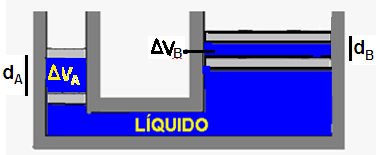
Princípio de Pascal
09-
Teorema de Arquimedes – Empuxo
10- Enunciado do princípio de Arquimedes:
“Todo corpo total ou parcialmente mergulhado num líquido em equilíbrio, recebe uma força de direção vertical e sentido para cima denominada de Empuxo, cuja intensidade é igual ao peso do volume de líquido deslocado“
R- A
11-
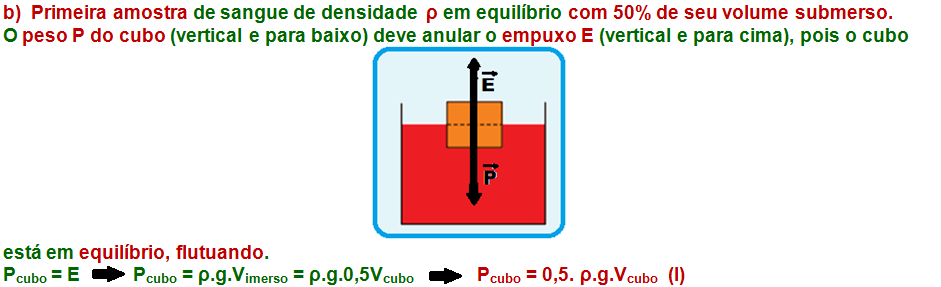
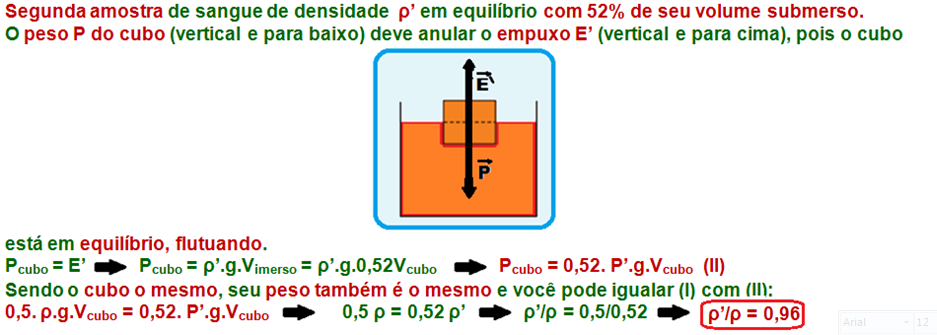
12-
Enunciado do princípio de Arquimedes
“Todo corpo total ou parcialmente mergulhado num líquido em equilíbrio, recebe uma força dedireção vertical e sentido para cima denominada de Empuxo, cuja intensidade é igual ao peso do volume de líquido deslocado“
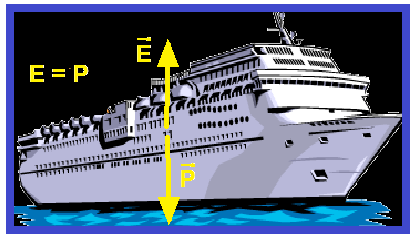
Como o navio está em equilíbrio vertical (flutuando) o empuxo (peso do volume do líquido deslocado), vertical e para cima deve ser igual ao peso do navio, vertical e para baixo.
R- C
13-
R- C
14-
15- Para esse exercício precisamos analisar a fórmula do empuxo:
E = dF.VFd.g
Onde:
E é o empuxo
é a densidade do fluído
VFd é o volume de fluído deslocado
g é a aceleração da gravidade
Com a adição de sal a densidade da água aumenta, porém quando se aumenta a densidade parte da esfera sai da água, e o volume deslocado diminui, sendo assim a alternativa D é a correta, pois o empuxo não se altera, já que o peso da esfera é o mesmo em ambos os casos.
16-
Massa do corpo sólido 
ms = 600g Vsólido = 1 L = 103 cm3 densidade do corpo sólido ds = 
ds = 
ds = 0,6 g/cm3.
Volume total = 1,0.10 3 cm3
Volume imerso = 80% do Vtotal = 0,8.103 cm3.
= 
= 
dl´quido = 
= 0,75 g/cm3.
R- B
17- Para que a pessoa + peso fique em equilíbrio é necessário que o empuxo (força vertical e para cima) equilibre os pesos da pessoa (Pp) somado ao peso do objetos (Po), verticais e para baixo.
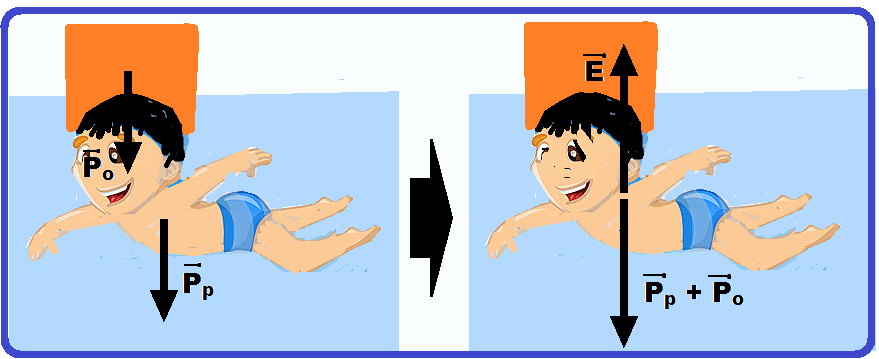
E = Pp + Po = mp.g + Po = 70.10 + Po E = 700 + Po.
Pessoa dpessoa = 
0,93.103 = 
Vpessoa = 
Vpessoa = 
= 75,27.10-3 m3.
Empuxo sobre a pessoa totalmente imersa E = dágua.Vpessoa.g = 103
. 75,27.10-3.10 E = 752,7 N.
E = 700 + Po 752,7 = 700 + Po Po = 752,7 – 700 Po = 52,7 N.
18-
Teorema de Arquimedes – Empuxo
“Todo corpototal ou parcialmente mergulhado num líquido em equilíbrio, recebe uma força dedireção vertical e sentido para cima denominada de Empuxo, cuja intensidade é igual ao peso do volume de líquido deslocado“
No caso do exercício peso total = peso da embarcação = mg=10.000×10 = 100.000 N + peso dos dois caminhões = 2.mg = 2.10.000×10 = 200.000 N + peso da carga dos dois caminhões = 2.m.10 =20m.
Ptotal =300.000 + 20m sendo m a massa de cada caminhão.
Volume imerso = Vi = área da base x altura = 10.10.0,4 
Vi =40m2.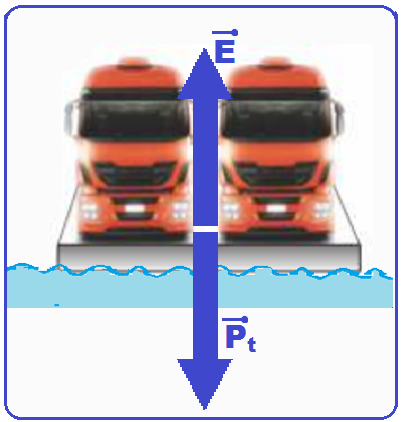
Densidade da água da = 1g/c3 = 103 kg/m3.
Cálculo do empuxo 
E = da.Vi.g = 103.40.10 E = 400.000 N
Como flutua parcialmente imerso está em equilíbrio vertical e a força resultante sobre ele é nula, assim o peso total deve anular o empuxo Pt = E 300.000 + 20m = 400.000 m = 100.000/20 m = 5.000 kg.
R- D
19- De acordo com o Princípio de Arquimedes todo corpo imerso sofre ação de uma força, denominada empuxo, que é vertical para cima, sua intensidade é igual ao peso do fluido deslocado pelo corpo. No caso do estudante, o volume deslocado foi utilizado, visto que a garrafa sempre estaria ocupando esse volume, com isso ele economizou, pois o vaso não enche tanto, não gasta tanta água e ainda por cima não interfere no rendimento da descarga.
R- A