Resolução comentada HIDROSTÁTICA – 2014 – 2013

Resolução comentada

HIDROSTÁTICA – 2014 – 2013.

01- O Empuxo (força vertical e para cima) corresponde ao peso do volume de líquido (no caso,

água)deslocado pela parte imersa do bloco e, pelo enunciado esse volume tem massa m com peso fornecido por P_água=m.g=E— por outro lado, o bloco encontra-se em equilíbrio (força resultante nula) flutuando na água

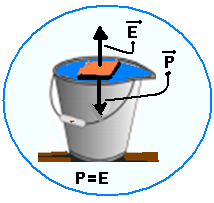
e assim, seu peso P_bloco (vertical e para baixo) deve anular o empuxo E (vertical e para cima) — P_bloco=M.g=E=P_água— m,g = M.g — m=M — R- C

02- A imagem vista pelo observador é virtual e está sempre acima do objeto e, ambos na mesma

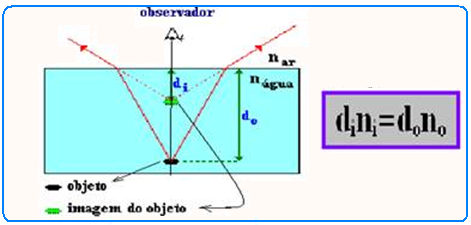
reta vertical, onde:

d_i—- distância vertical da imagem à superfície de separação (interface) água-ar (distância aparente, em que o observador enxerga a imagem)

d_o—- distância vertical do objeto, até a superfície de separação (interface) água-ar.

n_o—- índice de refração do meio onde está o observador (no caso, ar)

n_i—- índice de refração do meio onde está o objeto a imagem (no caso, água)

Pelas informações do exercício:

Então, o observador verá a imagem do fundo da piscina a uma distância d_i=2,25m abaixo da superfície da

água e, terá a impressão de vê-lo a uma altura h=3,00 – 2,25 = 0,75 m mais próximo em relação à profundidade real — R- C

03-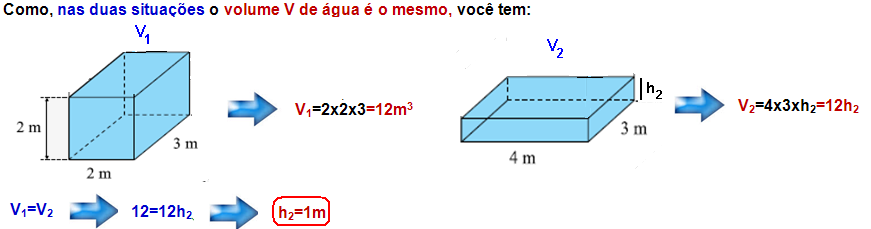

A pressão hidrostática no fundo de cada recipiente é fornecida pelo teorema de Stevin — P= d.g. h . No volume 1 de altura 2m— P₁=d_água.g.h₁= d_água.g.2 — P₁=2d_água.g.

No volume 2 de altura 1m — P₂=d_água.g.h₂= d_água.g.1 — P₁=d_água.g.

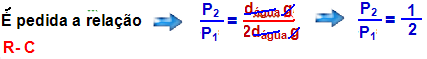
04- Peso — sendo a densidade do cilindro do lado direito maior que a do cilindro do lado esquerdo, o cilindro do lado direito terá maior massa, pois d=m/v (nessa expressão, como o volume V é o mesmo a massa m é diretamente proporcional à densidade d) — pela expressão P=m.g, quanto maior a massa maior o peso e o peso do cilindro direito é maior que o do cilindro esquerdo (ambos aplicados no centro geométrico) veja

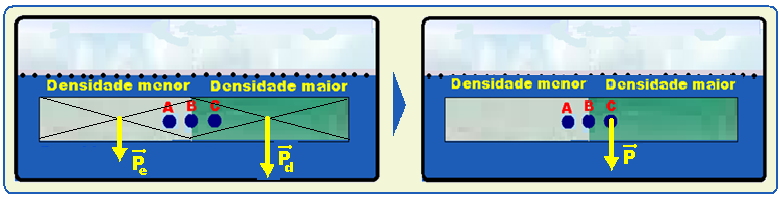
primeira figura — assim, o peso da boia será deslocado para o lado direito (ponto B) figura da direita.

Empuxo — Enunciado do princípio de Arquimedes:

“Todo corpo total ou parcialmente mergulhado num líquido em equilíbrio, recebe uma força de direção vertical e sentido  para cima denominada de Empuxo, cuja intensidade  é igual ao peso do volume de líquido deslocado“

Considere um líquido de densidade d_l contido num recipiente R’ no nível indicado na figura I, onde está um corpo sólido de densidade d_ctal que d_c > d_l.

Em seguida o corpo é colocado em R’ e  fica totalmente imerso (d_c > d_l), expulsando um volume de líquido que é igual ao próprio volume do corpo. O volume total (V) do líquido deslocado é recolhido no recipiente R (figura II).

Se você pesar o volume V do líquido deslocado você obterá o valor do empuxo, que é uma força vertical e para cima  —  empuxo=peso do volume de líquido deslocado (que é o mesmo volume que o do corpo, se totalmente imerso)  — E= P_l=m_lg  —  d_l=m_l/V  —  m_l=d_l.V_l  —  E=d_l.V_l.g

No caso do exercício, com a boia totalmente imersa ela deslocará um volume de água igual ao seu próprio volume — o empuxo, vertical e para cima, corresponde ao peso do volume de água deslocada e, como a água é um líquido homogêneo (mesma densidade em todos seus pontos) o empuxo será aplicado em seu

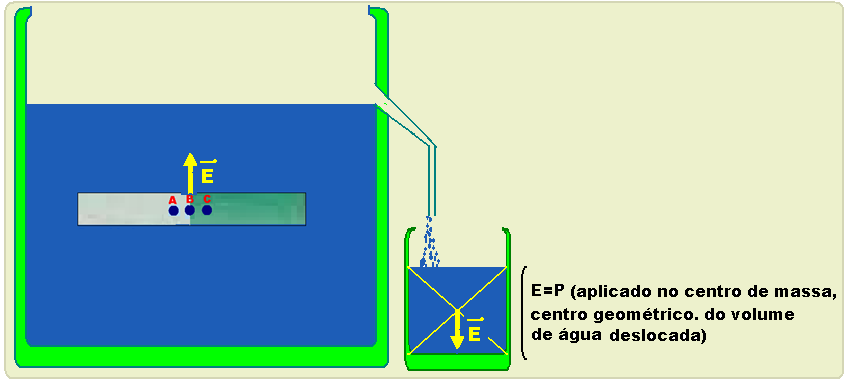
centro de massa que é onde é aplicado seu peso e que corresponde ao centro geométrico da boia

(ponto B) — R- C

05- Sobre a bexiga imersa agem as forças (peso, vertical e para baixo) e o (empuxo, vertical e para cima), tal que:

R- B

06- Como, em ambos os casos a esfera está flutuando o empuxo em cada um deles é igual ao peso da esfera que é o mesmo, pois P=mg e a massa é a mesma para cada esfera — já o líquido 2 é mais denso que o líquido 1, sendo mais pesado ficando mais embaixo, fazendo com que a esfera fique mais acima.

R- D

07- Como o objeto de volume V flutua no líquido ele está em equilíbrio e, nesse caso, o empuxo E

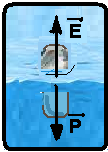
(força vertical e para cima) deve anular o peso P )força vertical e para baixo_.

Empuxo — E = d_líquido.V_imerso.g= d_líquido.(3/4)V.g.

Peso do objeto de volume V — P=d_objeto.V.g=600.10^-3.V.g — P=0,6Vg.

E = P — d_líquido.(3/4)V.g = 0,6Vg — d_líquido=2,4/3=0,8g/cm³

R- D

08- O objeto flutua (equilíbrio) com 2/3 de seu volume imerso V_i=V/3 — E = P — ρ.g.V_i =P — ρ.g.2V/3 = ρ_o.g.V — ρ.2/3 = ρ_o.

R- C

09- I. Correta — a atmosfera terrestre é uma imensa camada de ar e outros gases, com dezenas de quilômetros de altura, que são atraídos pela gravidade da Terra e por isso, sua densidade é maior em pontos mais próximos da superfície. Ela atua como uma zona intermediária entre o espaço sideral e a Terra e acompanha todos os movimentos da Terra.

      

Essa camada gasosa exerce uma pressão sobre os corpos nela mergulhados, devida ao peso da coluna de ar que se encontra sobre esses corpos, e que é chamada de pressão atmosférica, sendo tanto maior quanto mais o corpo estiver mais perto da superfície da Terra.

II. Correta — princípio enunciado por Pascal, físico e matemático francês (1623 – 1663), conhecido como princípio de Pascal:

“ O acréscimo de pressão exercido num ponto de um líquido ideal em equilíbrio é transmitida integralmente a todos os pontos desse líquido e também às paredes do recipiente onde está contido”

A maioria dos sistemas multiplicadores de forças é baseado no princípio de Pascal e, para explicá-lo considere um líquido ideal no interior de dois cilindros verticais de seções diferentes e interligados. Esses cilindros, em contato com a parte superior do líquido, possuem dois êmbolos de áreas S₁ e S₂.

 

Uma força de intensidade F₁ aplicada ao êmbolo de menor área (S₁), provocará um aumento de pressão dado por ΔP=F₁/S₁ e, pelo princípio de Pascal esse acréscimo de pressão se transmitirá integralmente a todos os pontos do líquido e das paredes, inclusive para o êmbolo de maior área (S₂). Então, o êmbolo maior fica sujeito a uma força F₂, tal que ΔP=F₂/S₂. Pelo princípio de Pascal essa variação de pressão se transmite integralmente  do êmbolo menor ao êmbolo maior e são iguais  —  F₁/S₁=F₂/S₂

Observe na expressão acima que, como S₂ > S₁, tem-se que F₂ > F₁ e, assim, a intensidade da força é proporcional à área de cada êmbolo, ou seja, esse sistema é capaz de multiplicar forças.

 Exemplos de sistemas multiplicadores de forças baseados no Princípio de Pascal:

 

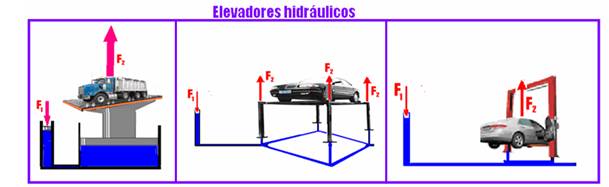
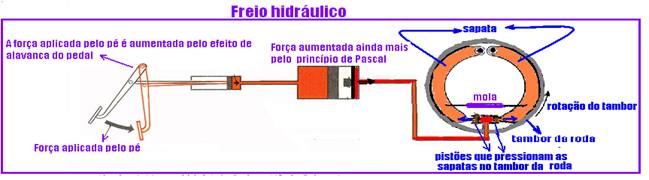
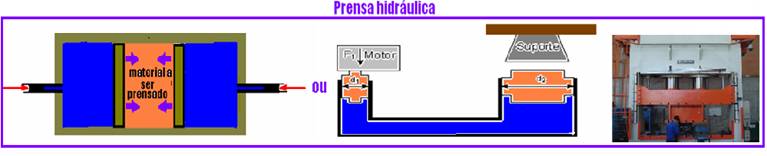
III. Correta — os mais densos, mais pesados, ficam em baixo e os menos densos, mais leves, ficam em cima

IV. Falsa — o empuxo é uma força exercida de baixo para cima sobre qualquer corpo imerso num fluido e é igual ao peso do volume de fluido deslocado “Principio de Arquimedes”

R- A

10- Peso de cada corpo — P_c=d_c.v_cg=m_cg — Empuxo de cada corpo — E=d_L.V_i.g — como estão flutuando estão em equilíbrio e P = E — m_c.g = d_L.V_i.g — V_i=m_c/d_L — como a massa do corpo é a mesma e o líquido é o mesmo (mesma d_L) o volume imerso é o mesmo para os três sólidos.

R- D

11- Pressão (P) é uma grandeza física obtida pelo quociente entre a intensidade da força () e a área  (S) em que a força se distribui. Observe na figura abaixo que a força () que produz a pressão sobre a área S é perpendicular à mesma.

 

No caso do exercício a força é a hidrostática, devida à pressão hidrostática e também é

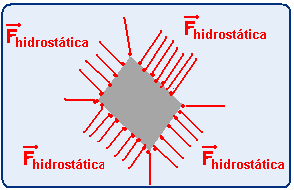
perpendicular à área da superfície em cada ponto.

R- A.

12- a) A pressão na interface água-mercúrio no ramo esquerdo do tubo (ponto k), pelo teorema de Stevin é dada por P

Stevin é dada por P_K=P_{atm +}  ρ_água.g.(h₂ + x + h₁), sendo ρ_água a densidade da água.

b) Como conseqüência do teorema de Stevin, todos os pontos no mesmo nível horizontal suportam a

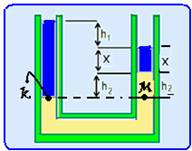
mesma pressão  —  P_K = P_M  —  P_{atm +}  ρ_água.g.(h₂ + x + h₁ = ρ_mercúrio.g.h₂ + ρ_água.g.x + P_atm  —  ρ_água.h₂ + ρ_água.h₁ = ρ_mercúrio.h₂  — h₁=(ρ_mercúrio – ρ_água)/ ρ_água.

13- O empuxo (força vertical e para cima) é igual ao peso do volume de líquido deslocado e assim, quanto maior o peso maior será o volume de líquido deslocado e consequentemente, maior será a altura da superfície da água do balde.

Maior peso B (barco + âncora dentro, deslocam maior volume de água) — menor peso A (barco sem

âncora, desloca menor volume de água) — intermediário C (volume deslocado somente pelo barco ) + volume deslocado somente pela âncora).

R- C

14- Pressão a que o submarino está sujeito no fundo do platô a uma profundidade de h=3600m — teorema de Stevin — P_f= P_atm + d_água.g,h= 10⁵ + 10⁵.10.3600 — P_f= 10⁵ + 36.10⁶ — P_f=361.10⁵ N/m².

É pedida a relação P_f/P_atm=361.10⁵/10⁵ = 361.

R- C

15- I. Correta.

II. Correta — E=d_água.g.h — observe nessa expressão que a relação entre E e h é uma função do primeiro grau.

III, Falsa — Teorema de Stevin — ΔP=d.g.h (a diferença de pressão é diretamente proporcional à altura h).

R. C

16- 05- A figura II indica o valor da pressão atmosférica P_atm=d_hg.g.h=13,6.10³.10.0,75 — P_atm=1,02.10⁵ Pa.

A pressão P_g exercida pelo gás é equilibrada pela pressão atmosférica (P_atm=10⁵Pa) somada à pressão devida ao mercúrio de densidade d_hg=13,6g/cm³=13,6.10³kg/m³ — P_g= P_atm + d_hg.g.h= 1,02.10⁵ + 13,6.10³.10.0,25=1,02.10⁵ + 34.10³=1,02.10⁵ + 0,34.10⁵ — P_g=1,36.10⁵ Pa.

R- 01

 

Densidade e pressão

47- 01. Correta  — A densidade de um corpo (no caso um líquido) pode ser definida como sendo a grandeza física que fornece a quantidade de massa (matéria)  de que está concentrada num determinado volume. Chamando de m a quantidade de massa contida em certo volume V, a expressão matemática da densidade é:

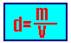
No Sistema Internacional de Unidades (SI) a unidade de densidade é o quilograma por metro cúbico (kg/m³), mas são usados também o grama por centímetro cúbico (g/cm³) e o quilograma por litro (kg/L). Relações:

1g=10-^-3kg  —  1cm3=10^-6m3   —  1g/cm³=10³kg/m³   —  1g/cm³=10^-3kg/10^-3L  — 1gcm³=1 kg/L

Regra prática:

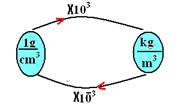
02. Correta  —  a pressão sempre vai estar relacionada ao módulo da força que age perpendicularmente à superfície  —  portanto, não importa em qual direção a força é exercida, ela na afeta a direção da pressão, que é sempre perpendicular a superfície  —  assim, o que interessa é só a intensidade da pressão.

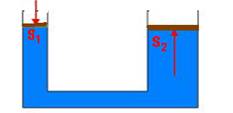
04. Correta  —  A pressão exercida por uma coluna líquida não depende das dimensões do recipiente que a contém, mas apenas da natureza do líquido, fornecida pela sua densidade (d), do local (g) e da altura da coluna (h)  —  entre dois pontos A e B de alturas h_A e h_B, a diferença de pressão é dada por (lei de Stevin)  —  P_A=d_líquido.g.h_A  —   P_B=d_líquido.g.h_B  —   ∆P=P_B – P_A= d_líquido.g.h_A – d_líquido.g.h_B  —  ∆P=d_líquido.g.(h_A – h_B).

08- Falsa —  são inversamente proporcionais  —  P=F/A  —  observe nessa fórmula  que para uma mesma força, quanto menor a área maior será a pressão exercida pela força  —  como exemplos práticos, observe as figuras abaixo:

 

 

 

16. Correta  — enunciado do princípio de Arquimedes:

“Todo corpo total ou parcialmente mergulhado num líquido em equilíbrio, recebe uma força de direção vertical e sentido  para cima denominada de Empuxo, cuja intensidade  é igual ao peso do volume de líquido deslocado“  —  trata-se do empuxo  —  E=d_líquido.V_{líquido deslocado}.g.

R- 01,02,04,16)

 

48- Água  —  Va=0,01m3=0,01.103dm3  —  Va=10L  —  da=1g/cm3=103kg/m3=103kg/103L  —  da=1kg/L  —  da=ma/Va  —  1=ma/10  —  ma=10L  —  óleo  —  Vo=2000cm3=2000.10-3dm3  —  Vo=2L  —  do=0,9g/cm3=0,9.103kg/m3=0,9.103kg/103L  —  do=0,9kg/L  —  do=mo/Vo  —  0,9=mo/2  —  mo=1,8kg  —  a massa da mistura vale  m=10 + 1,8=11,8kg  —  R- A.

 

Teorema de Stevin – Pressão hidrostática – Vasos comunicantes

 

37- Peixe 1  —  passou de 120m para 90m (desceu)  —  ∆P=d.g.∆h=10³.10.30=3.10⁵Pa=3atm  —  a

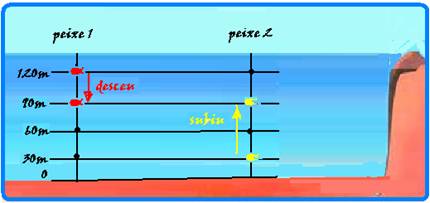
pressão aumentou  —  peixe 2  —  passou de 30m para 90m (subiu)  —  ∆P=d.g.∆h=10³.10.60=6.10⁵Pa=6atm  —  a pressão diminuiu  —

R- D.

 

38- Teorema Fundamental da Hidrostática ou de Teorema de Stevin  —  ∆P=d_água.g.h, onde P ´a pressão hidrostática no ponto de saída da água (onde está a ducha), g é a aceleração da gravidade local e h é altura medida desde qualquer

Ponto da superfície livre da água no interior da caixa d’água e o ponto de saída da mesma, onde está a ducha.

R- E.

 

Experiência de Torricelli

 

35- Os 5 primeiros cilindros estão ligados e, após abertas as válvulas eles atingirão o equilíbrio hidrostático e a altura final de cada um que deve ser a mesma (h) e dada por  —  h=(8 + 7 + 6 + 5 + 4)/5=6dm  —  observe na figura abaixo

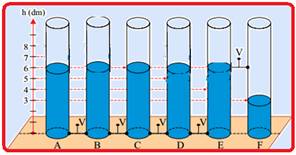
que a válvula que une E a F está na altura de 6dm e não escoará água de E para F que permanecerá na altura de 3dm  — 

R- A.

 

Princípio de Pascal

 

25- Se você chamar V1=V  —  V2=4V  —  se você chamar h2=h  —  h1=3h  —  V2=S2.h2  —  V1=S1.h1  —  4V = S2.h (I)  —  V=S1.3h (II)  —  (II) em (I)  —  4,3,S1.h = S2.h  —  S2=12S1  —  estando o sistema em equilíbrio a pressão em cada recipiente é a mesma  —  P1 = P2  —  F1/S1 = F2/S2  —  F1/S1 = F2/12S1  —  F1/F2=12  —  R- A.

26-  A maioria dos sistemas multiplicadores de forças é baseado no princípio de Pascal e, para explicá-lo considere um líquido ideal no interior de dois cilindros verticais de seções diferentes e interligados. Esses cilindros, em contato com a parte superior do líquido, possuem dois êmbolos de áreas S₁ e S₂.

 

Uma força de intensidade F₁ aplicada ao êmbolo de menor área (S₁), provocará um aumento de pressão dado por ΔP=F₁/S₁ e, pelo princípio de Pascal esse acréscimo de pressão se transmitirá integralmente a todos os pontos do líquido e das paredes, inclusive para o êmbolo de maior área (S₂). Então, o êmbolo maior fica sujeito a uma força F₂, tal que ΔP=F₂/S₂. Pelo princípio de Pascal essa variação de pressão se transmite integralmente  do êmbolo menor ao êmbolo maior e são iguais  —  F₁/S₁=F₂/S₂

Observe na expressão acima que, como S₂ > S₁, tem-se que F₂ > F₁ e, assim, a intensidade da força é proporcional à área de cada êmbolo, ou seja, esse sistema é capaz de multiplicar forças.

Substituindo os valores fornecidos  —  F₁/4.10^-4=2.10⁴/0,16  —  F₁=50N  —  R- C.

27- Observe na figura que a pressão na superfície de cada recipiente é a mesma e é a pressão atmosférica  —  no

recipiente da esquerda  —  P_atm=P_A + dgh  —  P_A=P_atm – dgh=P_atm – 10³.10.0,4  —  P_A= P_atm – 4.10³  —  no recipiente da direita  —  P_atm=P_B + dgh  —  P_B=P_atm – dgh=P_atm – 10³.10.1,2  —  P_B= P_atm – 1,2.10³  —  P_A – P_B= P_atm – 4.10³ – (P_atm – 12.10³)=P_atm – 4.10³ – P_atm + 12.10³  —  P_A – P_B=8.10³=8000Pa  —  R- D.

 

Teorema de Arquimedes – Empuxo

67- a) Área da base de cada cilindro A₁=A₂=A=π.R²=3.1²  —  A=3cm²  —  volume do cilindro 1  —  V=A.h₁=3.5  —  V₁=15cm³  —  volume do cilindro 2  —  V=A.h₂=3.0,5  —  V₁=1,5cm³  —  massa do

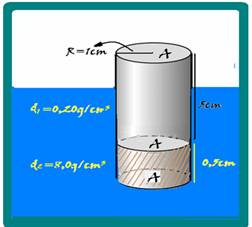
cilindro 1  —  d₁=m₁/V₁  —0,2=m₁/15  —  m₁=3g  —  massa do cilindro 2  —  d₂=m₂/V₂  —   8=m₂/1,5  —  m₂=12g  —   massa total  —  m=3 + 12=15g  —  m=15g ou m=15.10^-3kg.

b) Peso do cilindro  —  P=m.g=15.10^-3.10  —  P=15.10^-2N  —  cálculo do empuxo sobre o cilindro com volume imerso V_i  —  E=d_água.V_i.g=10³.V_i.10  —  E=10⁴V_i   —  como o está em equilíbrio o peso deve anular o empuxo  —  P=E  —

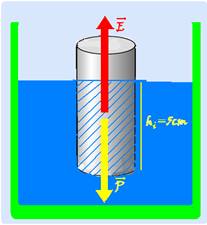
15.10^-2 = 10⁴V_i  —  V_i=15.10^-6m³  —  V_i=15cm³  —  altura (h_i) da parte imersa  —  V_i=S.h_i  —  15=3.h_i    —  h_i=5cm.

68- Peso do submarino sem lastro  —  P_s=m_s.g=13.10⁵.10=13.10⁶N  —  empuxo com o submarino totalmente imerso  —  E=d_água.V_s.g=10³.15.10².10=15.10⁶N  —  peso do volume V’ de água (lastro) que o submarino deve receber para que fique totalmente imerso e em equilíbrio  —  P’=d_água.V’.g=10³.V’.10=10⁴V’  —  como  ele está em equilíbrio a intensidade da força resultante

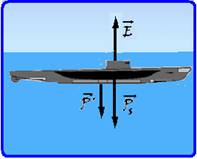
sobre ele deve ser nula  —  E = P_s + P’  —  15.10⁶ = 13.10⁶ + 10⁴V’  —  V’=2.10⁶/10⁴=

2.10²m³=200m³  —  R- B.

69- Peso do transatlântico  —  P=mg=1,2.10⁸.10=12.10⁸N  —  para que ele flutue sem tocar o fundo sua altura h deve ser tal que  —  V=b,L,h=300.40.h=12,10³h  —  empuxo  —  E=d_água.V.g. =

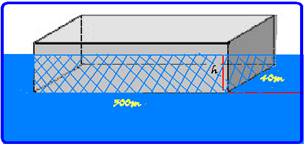
10³.12.10³h.10 = 12.10⁷h  —  como ele deve estar flutuando (em equilíbrio)  —  E = P  —  12.10⁷h=12.10⁸  —  h=12.10⁸/12.10⁷  —  h=10m  —  R- A.

70- Quando o ar do interior do balão é aquecido, ele se dilata, tornando sua densidade e, consequentemente seu peso menor  —  quando o peso do balão (vertical e para baixo) fica menor que o empuxo sobre ele (vertical e para cima), o balão sobe  —  R- A.

 

Voltar para os exercícios