Resoluções – Gravitação – 2013-2014

RESOLUÇÕES

2013 – 2014

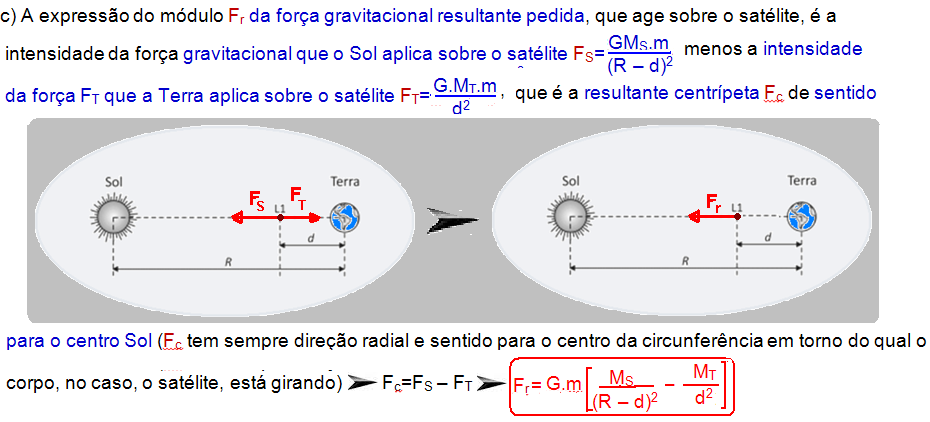
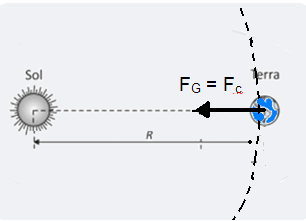
 01- a) O “Note e adote” afirma que você pode considerar as órbitas como sendo circulares e, assim, a Terra executa um movimento circular uniforme (MCU) em torno do Sol com velocidade angular W_T constante — então, a força gravitacional F_G que o Sol de massa M_S aplica sobre a Terra de massa M_T será a força resultante centrípeta F_c que é responsável por manter a Terra em órbita circular ao redor do Sol — F_G = F_c

b) A velocidade angular orbital W_A do satélite pedida é a mesma que a da Terra W_T já que ambos, satélite e Terra giram alinhados ao redor do Sol “varrendo” a mesma área no mesmo tempo — W_A=W_T=2/T, onde T é o período de rotação da Terra em torno do Sol e pelo “Note e adote” T=1 ano=3,14.10⁷s — W_A=2×3,14/3,14.10⁷ — W_A=2.10^-7 rad/s.

02- Gravidade artificial – Na Terra estamos acostumados com a “sensação se peso” e que quando estamos apoiados ela (sensação de peso) ocorre devido à força de reação normal  do apoio sobre nosso corpo.

Estando em equilíbrio e  possuem a mesma intensidade, ou seja, N=P  —  N=m.g— como a massa m é sempre constante, se variarmos a “gravidade” g, estaremos variando essa “sensação de peso”.

 Essa “sensação de peso” pode ser obtida fazendo a estação espacial, que deve ter a forma de um cilindro oco, efetuar movimento contínuo de rotação com velocidade angular W.

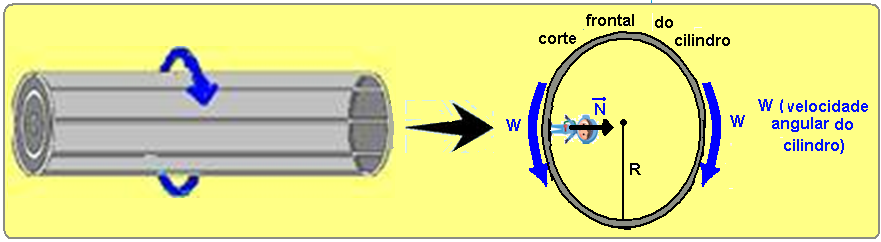
Essa simulação da “gravidade” ocorre, pois todo corpo em movimento circular tende a se afastar do centro e, no caso, “colando” nas paredes internas do cilindro— o“peso aparente” do astronauta é percebido pela reação normal  das paredes da nave sobre ele, que é a própria força resultante centrípeta F_c=m.V²/R, que deve ser igual ao peso do astronauta na Terra onde g==10m/s² — portanto, para que as pessoas tenham a sensação de peso, como se estivessem na Terra a condição é —N=P com N=mW²R e P=mg — no caso do exercício são dados — R=100m — g=10m/s² — portanto, N=P — mW²R=mg — W².100=10 — W=√(10/100) — W=√(0,1)≈0,316 rad/s — R- B

03- Titã está a uma distância média de 1 200 000 km de Saturno e tem um período de translação de, aproximadamente, 16 dias terrestres ao redor do planeta:

T_Titã=16d e r_Titã=1 200 000km=12.10⁵km.

Tétis é outro dos maiores satélites de Saturno e está a uma distância média de Saturno de 300 000 km e pede-se seu período de translação ao redor de Saturno:

T_Tétis=? — r_Tétis=300 000km=3.10⁵km.

Aplicando a terceira lei de Kepler:

R- B

04-

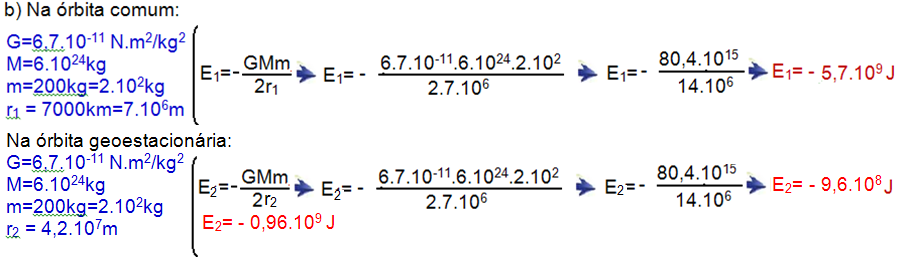
Energia adicional  E_a= – 0,96.10⁹ – ( – 5,7.10⁹)  E_a= 4,74.10⁹ J

05- Satélites geoestacionários  ou geosincrônicos (sincronizados com o movimento de rotação da Terra) — A maioria dos satélites de telecomunicações são satélites geoestacionários pois se encontram parados em relação a um ponto fixo sobre a Terra.

Seu período é o mesmo que o da Terra (24h), o raio de sua órbita é de, aproximadamente 36000km, tem a mesma velocidade angular (W) que a Terra e se encontram em órbitas sobre a linha do equador.      

R- A

06- Satélites geoestacionários  ou geosincrônicos(sincronizados com o movimento de rotação da Terra) — A maioria dos satélites de telecomunicações são satélites geoestacionários pois se encontram parados em relação a um ponto fixo sobre a Terra.

Seu período é o mesmo que o da Terra (24h), o raio de sua órbita é de, aproximadamente 36000km, tem a mesma velocidade angular (W) que a Terra e se encontram em órbitas sobre a linha do equador.                      

Acima da altura aproximada de 36000km o período do satélite aumenta e abaixo desse valor, diminui.

R- D 

07- Se você não domina o conteúdo, leia atentamente a teoria a seguir: Para colocar um objeto em órbita ao redor da Terra, como fazemos com os satélites artificiais, a partir de sua superfície da Terra, devemos lançá-lo com uma velocidade mínima, que denominamos velocidade de escape V_e).

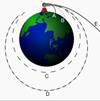
Essa velocidade mínima  (V_e) deve ser a velocidade  necessária para que um objeto, sem propulsão própria, saia da superfície da Terra e chegue no infinito com velocidade zero.

Assim, considerando:

G —  constante gravitacional

M —  massa da Terra

M —  massa do objeto a ser lançado com velocidade V_e e que vai escapar do campo gravitacional

r=R —  Distância entre o centro do planeta (Terra) e o ponto no qual a velocidade de escape está sendo calculada (superfície da Terra)

Energia mecânica na superfície da Terra de raio R

Energia potencial gravitacional  — E_p=-GMm/r — E_p=-GMm/R — Energia cinética — E_c=mV_e²/2

E_MT=E_c+E_p  — E_MT=mV_e²/2 – GMm/R

Energia mecânica no infinito

Energia potencial gravitacional — E_p=-GMm/ —  E_p=0 — Energia cinética  — E_c=m0²/2 — E_c=0 —

Energia mecânica — E_M¥=0 — pelo princípio da conservação da energia mecânica — E_MT=E_M¥

mV_e²/2 – GMm/R=0  — V_e=√(2GM/R)

 

Substituindo os valores de G, M, e R que conhecemos, obtemos:

V_e=11,3km/s que é a velocidade com que um corpo, sem propulsão própria deve sair da superfície da Terra para “libertar-se” de seu campo gravitacional.

Como a velocidade de um corpo em órbita é dada por V=√(GM/R) e a velocidade de escape por V_e=√(2GM/R), a velocidade de escape na altura R é √2 vezes maior que a velocidade em órbita circular na mesma altura.

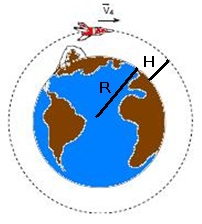
Assim, velocidade escalar adicional que o satélite precisa adquirir para escapar completamente do planeta.

deve valer — V_e=√2. √(2GM/(R + H) – √(2GM/(R + H) — R- D

08- R_Ma=4R_Me — T_Me=T_T/4 — Terceira lei de Kepler — T_Ma²/R_Ma³ = T_Ma²/R_Me³ — T_Ma²/(4R_Me)³ =

(T_T/4)²/R_Me³ — T_Ma²/64R_Me³ = T_T ² /16R_Me³ — T_Ma²/64 = T_T ² /16 — 4T_Ma² = 64T_T² — T_Ma²= 4T_t² —

T_Ma=2T_T.

R- B

Leis de Kepler

 

28- Segunda lei de Kepler (lei das áreas) 

“ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais  aos tempos

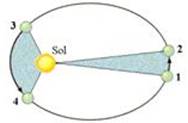
 gastos para percorre-las”

Sendo as áreas proporcionais  —  regra de três  —  A – 2 meses  —  αA – 32 meses  —  2.αA=32.A  —  α=16;

 29– I. Falsa  —  a primeira lei de Kepler afirma que as órbitas são elípticas com o Sol ocupando um dos focos da elipse.

II. Verdadeira  —  Segunda lei de Kepler (lei das áreas)  —  “ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais  aos tempos gastos para percorrê-las”

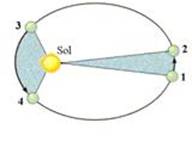
Sejam:

A₁— área entre 1,2 e o Sol  —  A₂— área entre 3, 4 e o Sol  —  ∆t₁— tempo que o planeta demora para ir de 1 a 2  —∆t₂— tempo que o planeta demora para ir de 3 a 4  —  então:

A₁∆t₁ ~A₂/∆t₂=constante=K  —  essa constante K depende do planeta e recebe o nome de velocidade areolar

 Observe na expressão acima que quando A₁=A_2, ∆t₁= ∆t₁, ou seja, para o arco maior 34, ser percorrido no mesmo

intervalo de tempo que o arco menor12, a velocidade em 3,4 (mais perto do Sol – periélio) deve ser maior que a velocidade em 1,2 (mais afastado do Sol – afélio).

Portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio.

III. Falsa  —  veja (II).

IV. Falsa  —  a órbita de Mercúrio não é circular, é elíptica.

 R- C.

 30- Leia atentamente a teoria a seguir:

 “ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais  aos tempos gastos para percorrê-las”

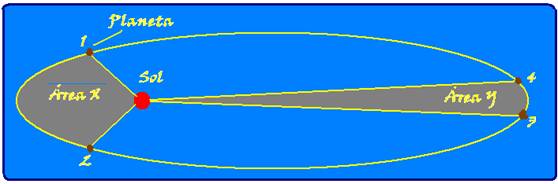
Sejam:

A_x— área entre 1,2 e o Sol  —  A_y  — área entre 3, 4 e o Sol  —  ∆t_x— tempo que o planeta demora para ir de 1 a 2  —

∆t_x — tempo que o planeta demora para ir de 3 a 4  —  pela lei das áreas de Kepler  —  A_x/∆t_x ~ A_y/∆t_y  —  essa constante K depende do planeta e recebe o nome de velocidade areolar.

 Observe na expressão acima que, quando A_x=A_y,  ∆t_x=∆t_y, ou seja, para o arco maior 34, ser percorrido no mesmo intervalo de tempo que o arco menor12, a velocidade em 3,4 (mais perto do Sol – periélio) deve ser maior que a velocidade em 1,2 (mais afastado do Sol – afélio).

Portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio. Ainda, de acordo com essa lei, se as órbitas forem circulares a velocidade de translação será constante e se a órbita do planeta tiver raio R e seu  período de translação for T, sua velocidade areolar (constante K) será dada por: K=A/∆t =πR²/T.

 R- B.

 

Lei da Gravitação Universal

16– Considere um planeta de massa m em órbita aproximadamente circular ao redor do Sol de massa M  —  a força gravitacional entre o planeta e Sol tem intensidade F_G=GMm/r², sendo G a constante de gravitação universal  e R a distância entre os centros do Sol e do planeta  —  a intensidade da força resultante centrípeta sobre o planeta vale F_c=mV²/R, sendo V a velocidade escalar (de translação) do planeta em torno do Sol  —  sobre o planeta essas duas forças são iguais  —  F_G = F_C  —  GMm/R² mV²/R  —  V=√(G.M/R)  —  observe por essa expressão que, quanto mais afastado o planeta estiver do Sol, menor será sua velocidade orbital e que essa velocidade não depende da massa m do planeta  —  assim, a velocidade orbital de translação da Terra é maior que a de Marte  —  esse é o motivo da trajetória em forma de laço, que você pode entender observando atentamente a figura abaixo.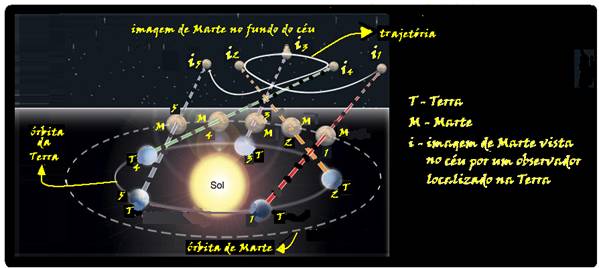

R- A.

 

SATÉLITES EM ÓRBITAS CIRCULARES

 

18- A velocidade orbital de um satélite ao redor de um planeta (no caso, a Terra) é fornecida por  —  V=√(GM/r)  —  G-constante gravitacional, M – massa da Terra e r – raio da órbita  —  são dados  — 

V_A=2.10³m/s  —  R_B/R_A=10²  — satélite A  —  V_A=√(GM/r_A)  —  2.10³=√(GM/r_A) (I)  —  satélite B  —  V_B=√(GM/r_B)  —  V_B=√(GM/10²r_A) (II).

(I)/(II)  —  2.10³/V_B=√(GM/r_A)/√(GM/10²r_A)  —  2.10³/V_B={√(GM)/√r_A}x{√(10²r_A)/√(GM)  —  2.10³/V_B=10√r_A/√r_A  —  10V_B=2.10³  —  V_B=2.10²m/s  —  R- D.

19- Dados  —  R=380 000km  —  T=28diasx24hx3600s=2 419 200s  —  π=3  —  V=2πR/T=2X3X380 000km/2 419 200s  —  V=0,94km/s  — R- E.

 20- 1. Falsa  —  A intensidade da força gravitacional entre cada satélite e o planeta P é dada por  —  F_g=GM_S.M_P/R²  —  observe nessa expressão que para o satélite S_A o raio da órbita é variável, assim a intensidade da força gravitacional entre o satélite S_A e o planeta P também é variável.

2. Verdadeira  —  Por meio de cálculos que fogem ao nível do ensino médio podemos demonstrar que a energia potencial gravitacional de um satélite em relação ao outro, adotando-se o referencial no infinito, é dada por:

Ep=-GMm/r  —  observe que essa energia potencial gravitacional é função da distância r entre os dois satélites, que é variável.

3. Falsa  —  essa afirmativa é válida para o satélite B  mas para o satélite B é falsa, pois em órbitas elípticas ele acelera do afélio para o periélio variando sua velocidade o que implica numa variação da energia cinética e da velocidade angular.

R- B. 

21- Satélites geoestacionários  ou geosincrônicos (sincronizados com o movimento de rotação da Terra)  —  a maioria dos satélites de telecomunicações são satélites geoestacionários pois se encontram parados em relação a um ponto fixo

sobre a Terra  —  seu período é o mesmo que o da Terra (24h), o raio de sua órbita é de, aproximadamente 36000km, tem a mesma velocidade angular (W) que a Terra e se encontram em órbitas sobre a linha do equador.                      

Acima da altura aproximada de 36000km o período do satélite aumenta e abaixo desse valor, diminui.

R- A. 

Aceleração da gravidade

 

18- Pelo enunciado eles possuem a mesma densidade  —  d_T=d_Y  —  d_T=m_T/V_T=m_T/(4/3)πR_T³  —  d_Y=m_Y/V_Y=m_Y/(4/3)πR_Y³ —  d_Y= m_Y/(4/3)π(3R_T)³  —  d_Y=m_Y/36πR_T³  —  d_T=d_Y  —  m_T/(4/3)πR_T³= m_Y/(4/3)36πR_T³  —  m_Y=27m_T  —  aceleração da gravidade na superfície da Terra  —  g=Gm_T/R_T²  —  aceleração da gravidade na superfície de Y  —  g_Y=Gm_Y/R_Y²=G.27m_T/(3R_T)²  —  g_Y=27Gm_T/9R_T²  —  g_Y=3.Gm_T/R_T²  —  g_Y=3g  —  R- E.

19- O peso do jipe na Terra  —  P_T=m.g_T  —  a massa do jipe é a mesma na Terra e em Marte  —  peso do jipe em Marte  —  P_M=m.g_M­  —  como, pelo enunciado, o veículo foi suave e lentamente baixado até o solo, ele se encontra em equilíbrio dinâmico e a força resultante sobre ele é nula  —  assim, a tração T nos cabos é igual ao peso, tanto na Terra como em Marte  —  P_T=T_T=m.g_T e P_M=T_M=m.g_M  —  a aceleração da gravidade na superfície  de um planeta é fornecida por  —  g=G.M/R²  —  G é uma constante, M a massa do planeta e R o raio médio do planeta  —  T_T=m.g_T=

m.GM_T/R_T²=mG.10M_M/(2R_M)²  —  T_T=2,5mGM_M/R_M (I)  —  T_M=m.g_M=m GM_M/R_M (II)  —  (II)/(I)  —  T_M/T_T=

(mGM_M/R_M)x (R_M/2,5GM_M)  —  T_M/T_T=1/2,5=0,4  —  R- C.

 

Voltar para os exercícios