Estática – 2020
MECÂNICA – Vestibulares recentes – 2020
DINÂMICA
ESTÁTICA
01– (CEDERJ-RJ-2020)

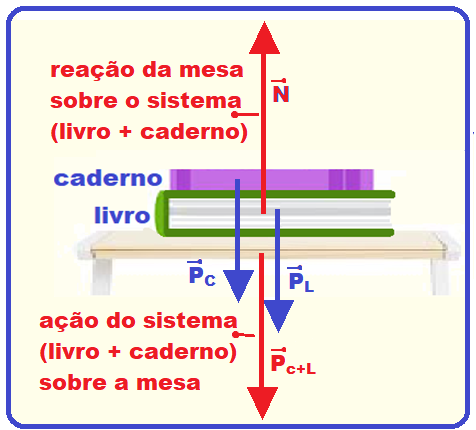
Sobre uma mesa parada se encontra um livro e sobre esse repousa um caderno.


Veja figura abaixo:
![]()
R- D
Estática de um ponto material
02– (Instituto Federal de Educação, Ciência e Tecnologia do Paraná – IFPR – 2020)

Uma pessoa aplica uma força F sobre o ponto P para manter um corpo “M” de massa de 15kg em equilíbrio estático, como mostra a figura.
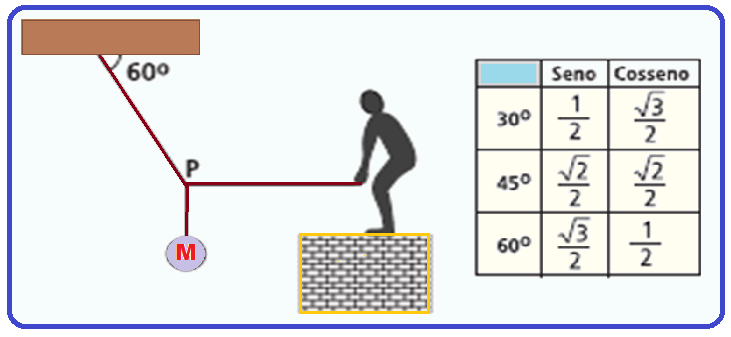
O ponto P está ligado ao teto por meio de uma corda, que suporta uma tração T, formando um
ângulo de 60º com a horizontal.
Considerando que a aceleração da gravidade vale 10 ![]() , calcule o valor da força F que a pessoa deve exercer sobre o ponto P e assinale a alternativa correta.
, calcule o valor da força F que a pessoa deve exercer sobre o ponto P e assinale a alternativa correta.

P = m.g = 15.10 = 150 N
Colocando as forças ![]() Figura 1
Figura 1
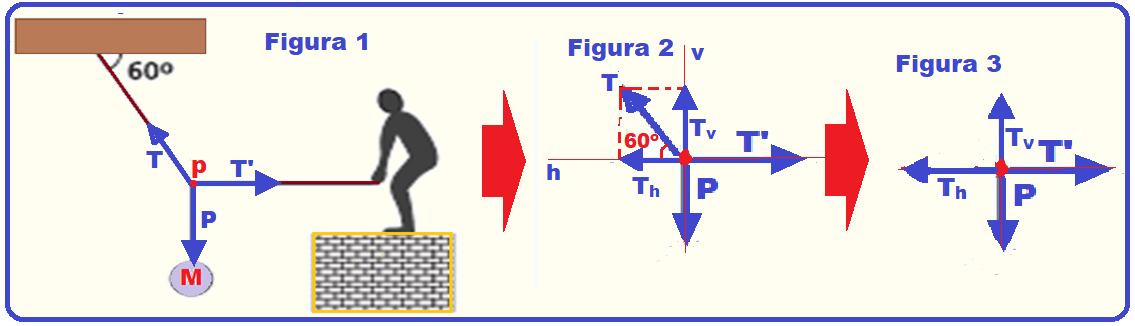

R- A
03– (ENEM-MEC-019)

Slackline é um esporte no qual o atleta deve se equilibrar e executar manobras estando sobre uma fita esticada.
Para a prática do esporte, as duas extremidades da fita são fixadas de forma que ela fique a alguns centímetros do solo. Quando uma atleta de massa igual a 80 kg está exatamente no meio da fita, essa se desloca verticalmente, formando um ângulo de 10° com a horizontal, como esquematizado na figura.
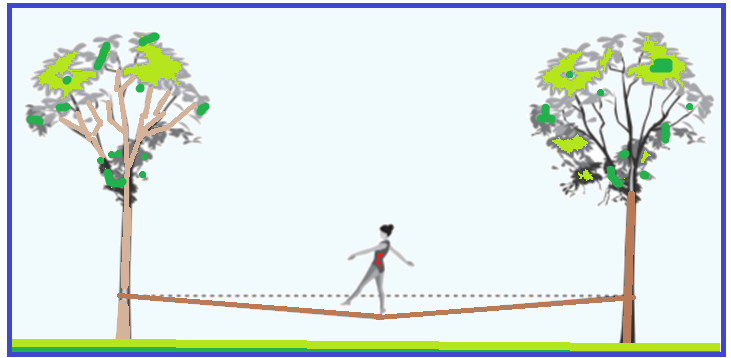
Sabe-se que a aceleração da gravidade é igual a 10 m.s−2, cos(10°) = 0,98 e sen(10°) = 0,17.
Qual é a força que a fita exerce em cada uma das árvores por causa da presença da atleta?
(A) 4,0×102 N
(B) 4,1×102 N
(C) 8,0×102 N
(D) 2,4×103 N
(E) 4,7×103 N)
Colocando as força que agem sobre a fita no ponto onde ela está em contato com o pé do atleta, que são:
Seu peso ![]() vertical e para baixo de intensidade P = m.g = 80.10
vertical e para baixo de intensidade P = m.g = 80.10 ![]() P = 800 N.
P = 800 N.
As duas forças de tração na fita que, como estão aplicadas no meio da mesma possuem a mesma intensidade T que é pedida (força que cada extremidade da fita troca com as árvores “ação e reação”)
Sendo o ângulo que a fita forma com a horizontal de 10o você terá situação da figura 1 abaixo:
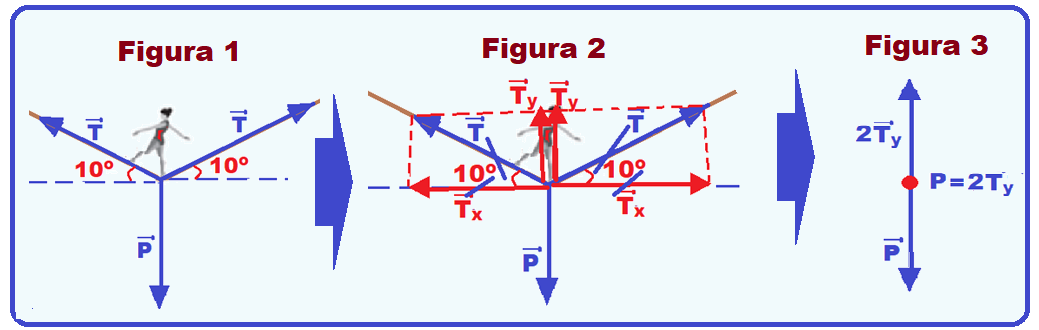

R – D
Estática de um corpo extenso
04– (EsPCEx – AMAN – SP – RJ – 2020)

Uma viga rígida homogênea Z com 100 cm de comprimento e 10 N de peso está apoiada no suporte A, em equilíbrio estático.
Os blocos X e Y são homogêneos, sendo que o peso do bloco Y é de 20 N, conforme o desenho abaixo.
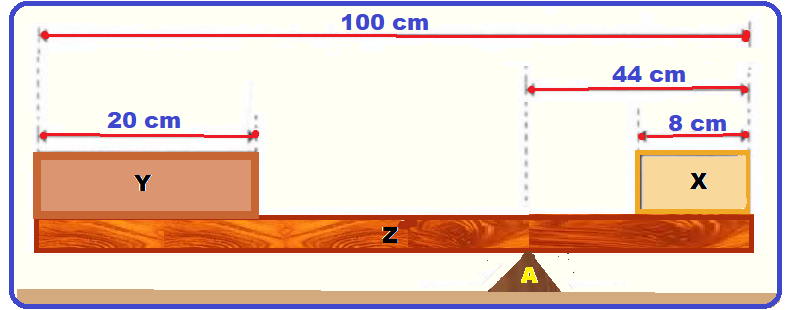
O peso do bloco X é
![]()
Condições de equilíbrio de um corpo extenso
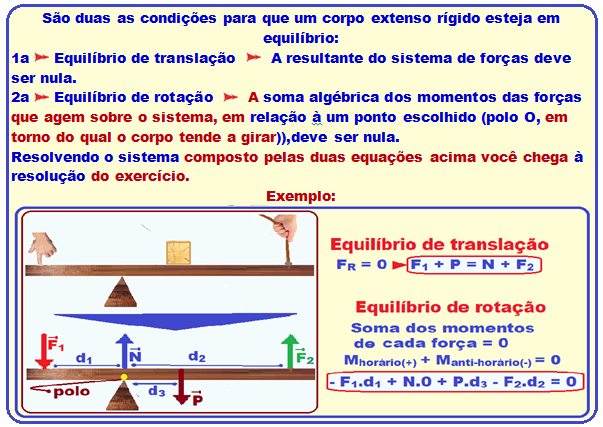
No caso do exercício inicialmente você deve colocar as forças peso que cada bloco exerce sobre a viga no centro de massa (centro geométrico) das mesmas;
Como a viga é homogênea seu peso deve estar no meio, a 50 cm de cada extremidade.
Colocar a reação do apoio N sobre a barra (vertical e para cima) no ponto de contato do apoio A com a barra.
Redistribuir as distâncias (figura abaixo).
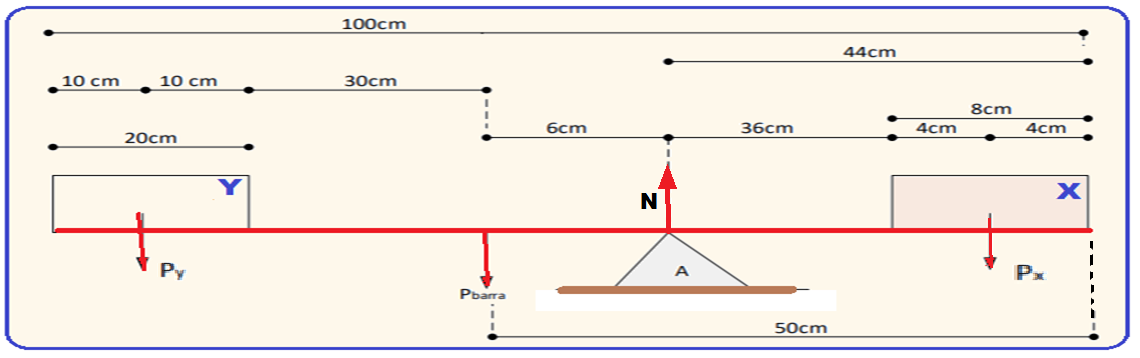
Para facilitar a figura a seguir mostra apenas as forças que interessam junto com as respectivas distâncias e o polo 0 (eixo de rotação) foi escolhido em N.
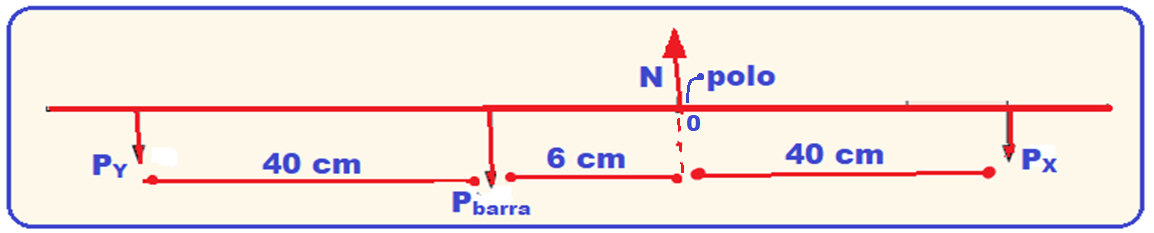
Cálculo do momento de cada força em relação ao polo estabelecendo o sentido horário de
rotação como positivo e o anti-horário como negativo.

R- E
05– (Faculdade de Medicina do ABC – FMABC – SP – 2020)

Ao praticar exercícios com barra, uma pessoa, inadvertidamente, colocou peso maior em um dos lados da barra, como mostra a figura.
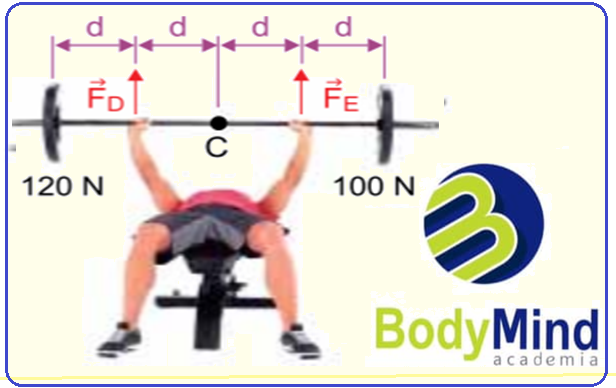
Considerando que a barra seja homogênea, indeformável e de peso 100 N, e que o ponto C seja o centro geométrico da barra, as intensidades das forças, supostas verticais,![]() que a pessoa deve aplicar na barra para mantê-la em equilíbrio na posição horizontal valem, respectivamente,
que a pessoa deve aplicar na barra para mantê-la em equilíbrio na posição horizontal valem, respectivamente,
(A) 160 N e 160 N.
(B) 190 N e 130 N.
(C) 170 N e 150 N.
(D) 180 N e 140 N.
(E) 200 N e 120 N.
Equilíbrio de um corpo extenso

Sendo a barra homogênea, indeformável seu peso P = 100 N está no centro geométrico C da mesma.
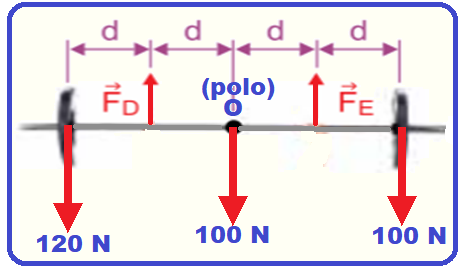
Colocando todas as forças que agem sobre a barra, colocando o polo O (eixo de rotação) no ponto C e calculando o momento de cada força em relação ao polo considerando o sentido horário de rotação em torno de O como positivo.
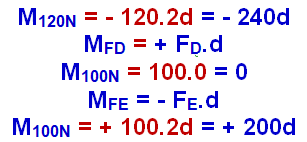

R- D
06– (FUVEST- SP- 2020 – Segunda Fase)

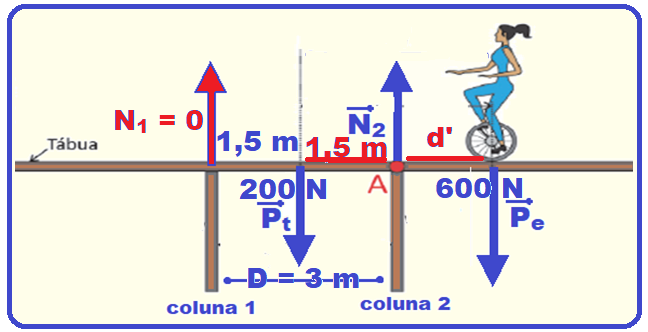
Uma equilibrista de massa M desloca‐se sobre uma tábua uniforme de comprimento L e massa m apoiada (sem fixação) sobre duas colunas separadas por uma distância D (D < L) de modo que o centro da tábua esteja equidistante das colunas.
O ponto de apoio da equilibrista está a uma distância d (tal que D/2 < d < L/2) do centro da tábua, como mostra a figura.
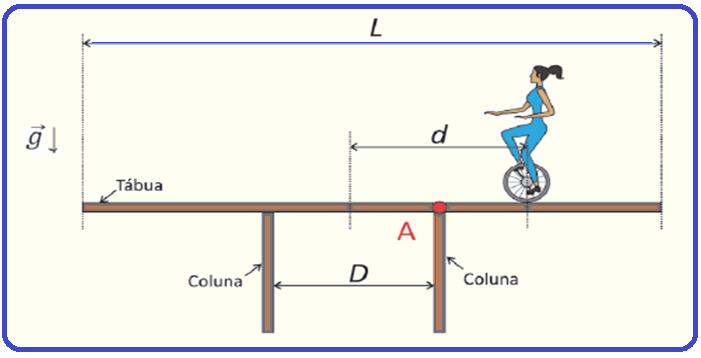
a) Considerando que a tábua está em equilíbrio, faça um diagrama indicando todas as forças que atuam sobre a tábua e seus respectivos pontos de aplicação.
b) Calcule o torque resultante exercido pelos pesos da equilibrista e da tábua em relação ao ponto A (ponto de apoio da tábua na coluna mais próxima da equilibrista).
Escreva sua resposta em termos de grandezas mencionadas no enunciado (M, L, m, D, d) e da aceleração da gravidade g.
c) Calcule a distância máxima ![]() da equilibrista ao centro da tábua para que o conjunto permaneça em equilíbrio estático.
da equilibrista ao centro da tábua para que o conjunto permaneça em equilíbrio estático.
Considere os seguintes dados: comprimento da tábua: L = 5 m; massa da tábua: m = 20 kg, massa da equilibrista: M = 60 kg, distância entre as colunas: D = 3 m.

a)
As 4 forças que agem sobre a tábua são 4 e estão na figura abaixo:
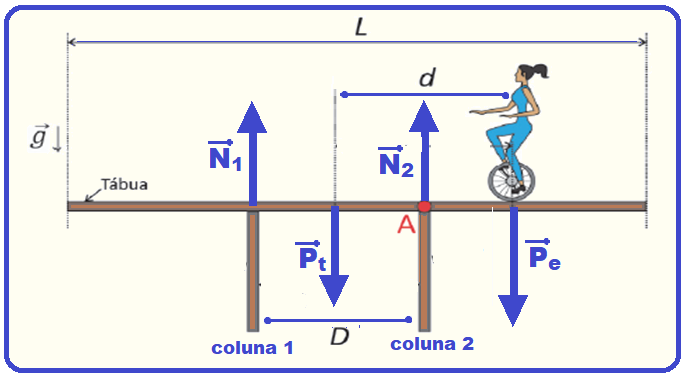

b) É pedido o torque (momento) resultante devido apenas aos pesos do peso da tábua ![]() e do equilibrista
e do equilibrista ![]() .
.
Cálculo do momento (torque) dessas forças com o polo em A e estabelecendo o sentido horário de rotação em torno do polo A como positivo.
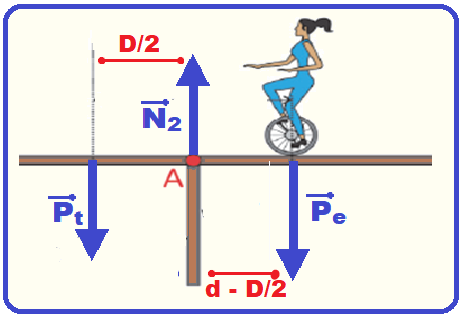
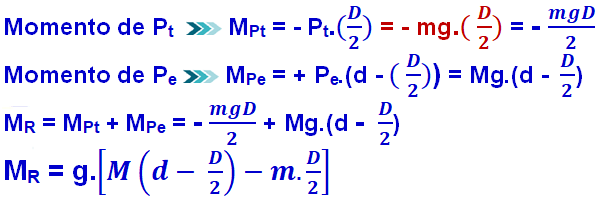
c) Considere os seguintes dados: comprimento da tábua: L = 5 m; massa da tábua: m = 20 kg, massa da equilibrista: M = 60 kg, distância entre as colunas: D = 3 m.


07– (IFSULDEMINAS – Instituto Federal de Educação, Ciência e Tecnologia do Sul de Minas Gerais – 2019/2020)

A figura a seguir mostra uma fina prateleira de madeira, com 20 N de peso e 0,6 m de profundidade,
presa a uma parede da seguinte forma: na extremidade da prateleira que está em contato com a
parede, a fixação é feita por uma dobradiça articulada e na outra extremidade por um cabo de metal
(inextensível e com massa desprezível):
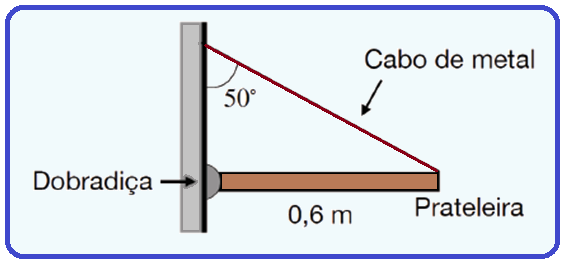
Deseja-se ajustar a tensão no cabo de metal para manter a prateleira em equilíbrio na direção horizontal, perpendicularmente à parede.
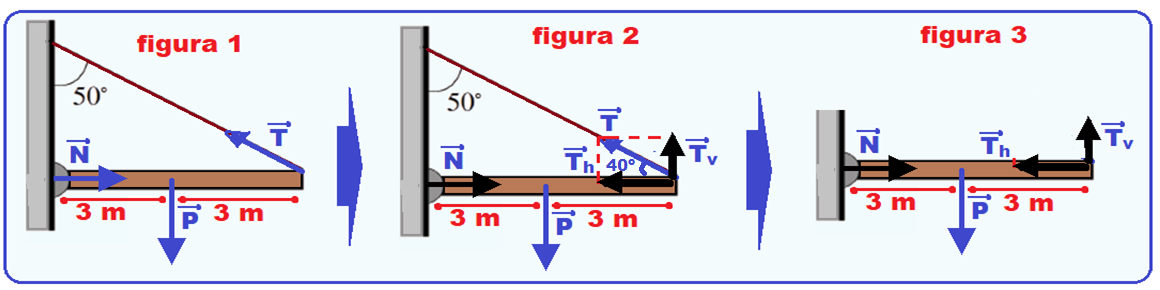
Dentre as alternativas a seguir, qual será, aproximadamente, o valor da tração no cabo de metal? Adote: sen 40º = 0,64.
a) 10,35 N
b) 18,41 N
c) 15,63 N
d) 31,25 N



R – C
08– (MACKENZIE – SP – 2020)

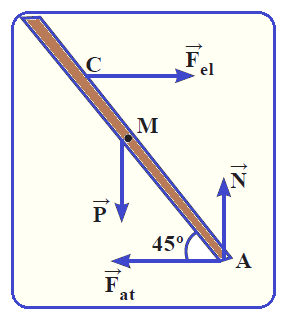
A barra da figura acima é homogênea, possui massa m = 30 kg e comprimento L = 4,0 m.
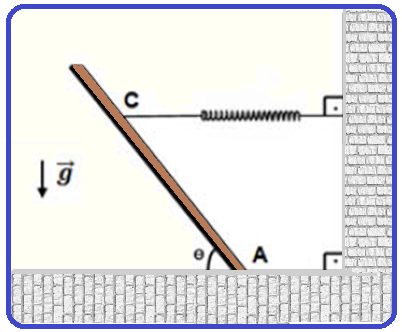
Ela está apoiada sobre o ponto A em um plano horizontal rugoso e é vinculada pelo ponto C, a um metro de topo da barra, a uma mola de constante elástica K.
Sabe-se que o campo gravitacional local tem módulo g = 10 ![]() e que o sistema encontra-se em equilíbrio quando Ө = 45º e a mola tem sua extensão máxima
e que o sistema encontra-se em equilíbrio quando Ө = 45º e a mola tem sua extensão máxima ![]() = 0,20 m.
= 0,20 m.
Com base nos dados fornecidos, pode-se afirmar que o valor de K, em kN/m, é
a) 5,0
b) 4,0
c) 3,0
d) 2,0
e) 1,0
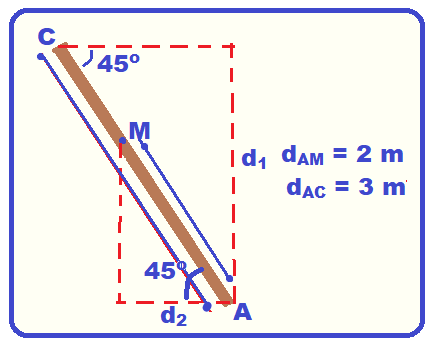
Cálculo do peso da barra que está localizado no centro de massa M da mesma, equidistante 2m de A e de C ![]() P = m.g = 30.10
P = m.g = 30.10 ![]() P = 300 N.
P = 300 N.
Colocando todas as forças que agem sobre a barra:


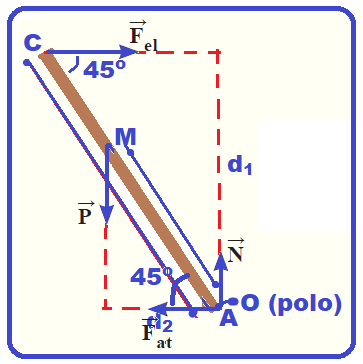

R- E
09– (PUCRS – 2020)

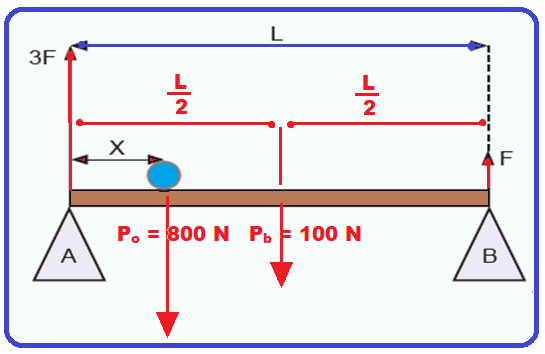
Dois pilares A e B sustentam, em posição horizontal, uma barra uniforme de 100 N e comprimento L. Um objeto com o peso de 800 N encontra-se apoiado na barra.
Para manter o sistema em equilíbrio, o pilar A exerce uma força 3F em uma das extremidades da barra.
Na outra extremidade, o pilar B exerce uma força F.
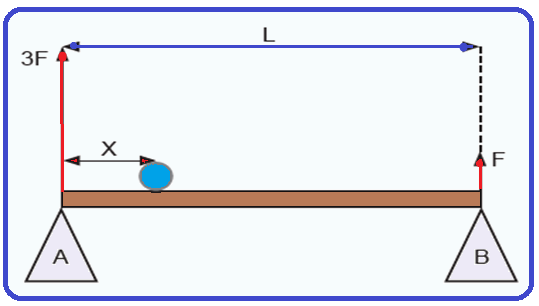
Qual o valor aproximado da distância X entre o pilar A e o objeto na barra?
A) 0,11 L
B) 0,22 L
C) 0,38 L
D) 0,44 L


R- B
10– (UERJ – RJ – 2020)

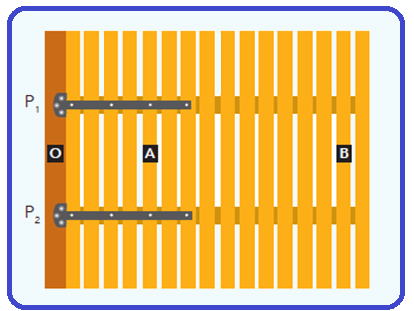
Um portão fixado a uma coluna está articulado nos pontos ![]() , conforme ilustra a imagem a seguir, que indica também três outros pontos: O, A e B.
, conforme ilustra a imagem a seguir, que indica também três outros pontos: O, A e B.

(A) 15
(B) 30
(C) 45
(D) 60
FA e FB forças perpendiculares nos pontos A e B empurrando o portão para dentro da página.
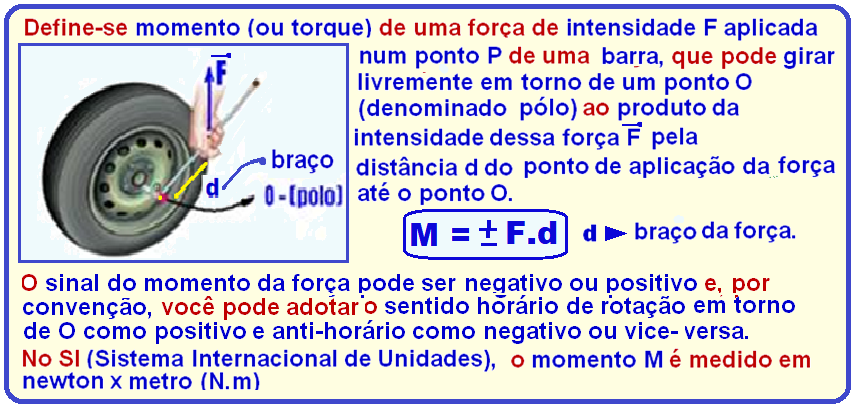
Momento (ou torque) de uma força

R- D
