Estática – Resolução Comentada – 2018/2019

01-

Observe a imagem abaixo:

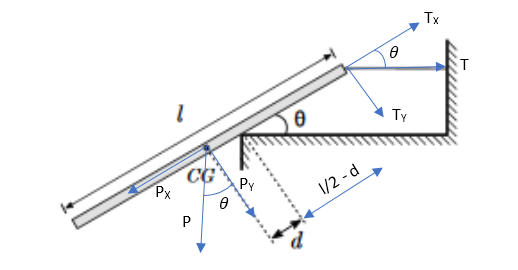
Em todos os exercícios de equilíbrio precisamos verificar os dois tipos – translacional e rotacional – começando pelo translacional, no caso só em X, pois em Y ela se equilibra com a normal do contato com a quina:

Observe que pelo desenho temos:

PX = P.senΘ

PY = P.cosΘ

TX = T.cosΘ

TY = T.senΘ

Agora o equilíbrio rotacional, lembre-se que, diferente das forças, a distância ao centro de massa importa:

Após bastante esforço, a alternativa correta é a E.

02-

Colocando as forças que agem sobre cada fio (figura 1) e decompondo-as (figura 2).

Observe na figura 3 que as projeções de T na horizontal de anulam (equilíbrio horizontal).

Projeção de T na vertical Ty = T.sen30o = 2k.0,5 Ty = 1 kN.

Equilíbrio na vertical 2Ty = P 2.1k = P P = 2 kN = 2000 N.

P = m.g 2000 = m.10 m = 2000/10 m = 200 kg.

R- D

03-

Inicialmente as balanças marcam o mesmo valor 40 kg que é igual à metade da massa do homem. Isso significa que ele está na metade da plataforma, equidistante 4 m de cada extremidade.

Situação depois quando ele se aproxima de uma das extremidades, por exemplo, a da direita, as balanças passam a marcar 20 kg (Pe = 20.10 = 200 N) a da esquerda e 60 kg (Pd = 60.10 = 600 N) a da direita.

Colocando o polo O na balança da esquerda, calculando módulo do momento de cada força em relação ao mesmo e estabelecendo o sentido horário de rotação como positivo:

Então, ao se deslocar ele passou da posição 4 m (antes) para a posição 6 m (depois), se deslocando

S = 6 – 4 = 2m

R – D

04-

Colocando as forças que agem sobre cada ponto da arara:

Peso da arara colocado no centro de massa da mesma localizado a da = 0,5 m de A e 0,5 m de B Pa = m.g = 1.10 = 10 N

Peso do conjunto 1 P1 = m1.g = 1.10 P1 = 10 N com d1 = 0,1 m de A

Peso do conjunto 2 P2 = m2.g = 0,5.10 P2 = 5 N com d2 = 0,3 m de A

Peso do conjunto 3 P3 = m3.g = 1,5.10 P3 = 15 N com d3 = 0,8 m de A

NA reação normal em A com dA = 0

NB reação normal em B com dB = 1m de A.

Colocando o polo (eixo de rotação) em A, calculando o momento de cada força em relação ao polo e estabelecendo o sentido horário de rotação em torno de A como positivo:

MNA = NA.0 = 0

MP1 = P1.d1 = 10.0,1 = 1 N.m

MP2 = P2.d2 = 5.0,3 = 1,5 N.m

Ma = Pa.da = 10.0,5 = 5 N.m

MP3 = P3.d3 = 15.0,8 = 12 N.m

MNB = – NB.1 = – NB

No equilíbrio de rotação a soma dos momentos de cada força em relação ao polo deve ser nula

0 + 1,0 + 1,5 + 5,0 + 12 – NB = 0 NB = 19,5 N

No equilíbrio de translação a soma das forças para cima de anular a soma das forças para baixo

10 + 5 + 10 + 15 = NA + NB 40 = NA + 19,5 NA = 40 – 19,5 NA = 20,5 N

R- A

05-

Sendo que o enunciado afirma que o peso e consequentemente a massa (P = m.g, com g constante) dos objetos (triângulos) é proporcional à sua área, vamos calcular a área de cada triângulo.

Como o enunciado afirma que a hipotenusa do triângulo retângulo tem o mesmo comprimento que os lados do triângulo equilátero, vamos denomina-los de .

Cálculo da área S do triângulo equilátero

Cálculo da área S do triângulo isósceles

06-

Causa da sustentação de um avião

R- B

07-

Equilíbrio na horizontal N1 = T.

Equilíbrio na vertical P = N.

Cálculo do momento de cada força que é o valor da força multiplicada pela distância do prolongamento da força até o polo 0 (colocado em B).

Com o polo em B vamos calcular o momento de cada força estabelecento o sentido horário d rotação como positivo:

MN1 = – N1.AM = – T.1,5

MP = + P.BN = 20..cos60o = 20.. MP = 15 N.m

No equilíbrio de rotação a soma dos momentos de cada força em relação ao polo deve ser nula

– T.1,5 + 15 = 0 T = = = T = N.

R- C

08-

09-

As forças peso do bloco P e a Terra (centro da Terra) constituem par ação e reação e as forças trocadas entre a mão e o bloco constituem par ação e reação.

R- B