Resoluções – Estática – 2015 – 2016 e 2017
Estática de um ponto material 2017 – 2016 – 2015
Resoluções
01-Denominando de ml a massa de cada cubo laranja e de ma a massa de cada cubo azul e, estando as balanças em equilíbrio, você terá:
Balança da esquerda
2ma + ml = 2 (I)
Balança da direita ma + 3 = 2ml (II)
Isolando ma em (II) e substituindo em (I) ma = 2ml – 3 2(2ml – 3) + ml = 2 4ml – 6 + ml = 2 5ml = 8 ml= 8/5 = 1,6 kg.
2ma + 1,6 =2 ma = 0,4/2 ma = 0,2 kg.
Assim, a massa de um cubo laranja supera a de um cubo azul em ml – ma= 1,6 – 0,2 = 1,4 kg.
R- D
02-
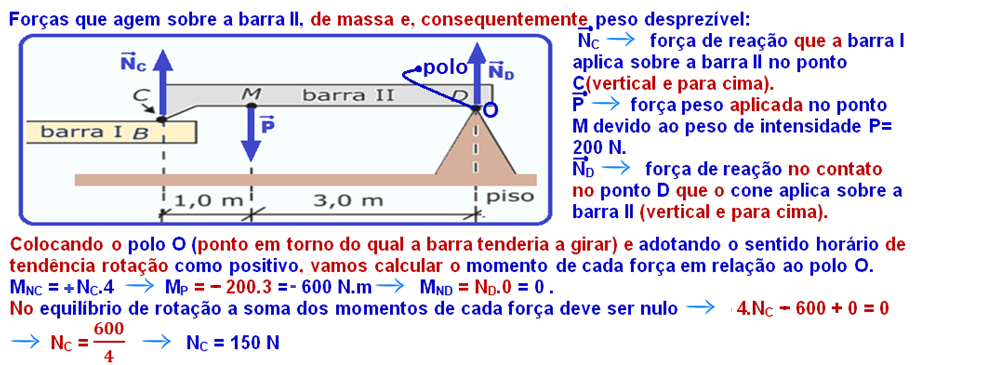
No equilíbrio de translação, para que ocorra equilíbrio na vertical a resultante das forças deve ser nula, ou seja, NA + NB = NN 
75 + 150 = NN NN = 225 N
R- D
03-
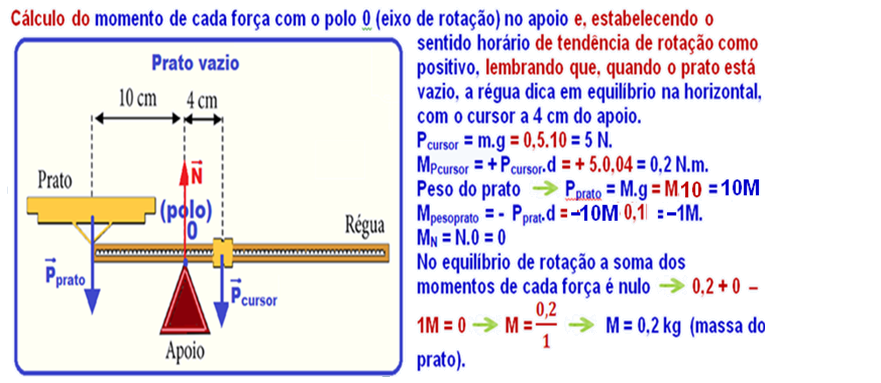
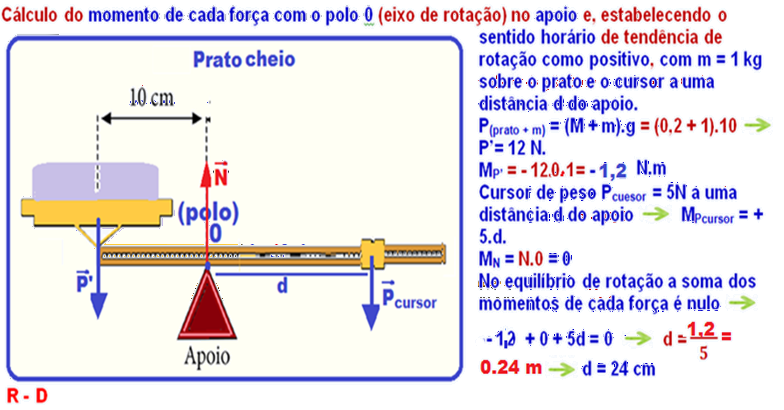
04- A) Colocando o polo (eixo de rotação) no ponto O, e estabelecendo o sentido de tendência de rotação em torno de O como positivo para o horário e negativo para o anti
horário, vamos calcular o momento (torque) de cada força em relação a O, sendo dP e dm as distâncias entre o ponto de aplicação das forças O até as forças FP e Fm:
MP = P.d = P.0 = 0
MFP = + FP.dP
MFm = – Fm.dm
A condição de equilíbrio de rotação é de que a soma dos momentos (torques) de cada força seja nula
0 + FP.dP – Fm.dm = 0 FP.dP = Fm.dm Fm = FP.dP/dm.
B) O momento (torque) exercido pelo prego sobre o martelo (e vice versa) é fornecido e tem intensidade MP = FP.dP = 30 Nm com dm = 0,2 m, que substituidos em Fm = FP.dP/dm fornrcem Fm = 
Fm = 150 N.
C) Aquí o peso de intensidade P participa e sua distância ao polo é d, e astrês forças que influem na rotação tem intensidades P, Fp e Fm, cujosmomentos (torques) em relação à O, estabelecendo o sentido de tendência de rotação em torno de O como positivo para o horário e negativo para o anti horário, serão:
MP = – P.d
MFm = – Fm.dm = – Fm.20d = – 20dFm
MFP = + FP.dP = + FP.4d = + 4dFP
No equilíbrio de rotação a soma desses momentos deve ser nula – P.d – 20dFm + 4dFP = 0 20Fm = P – 4FP Fm = (P – 4FP/20 = 
– 
05- Para esse exercício precisamos analisar a fórmula do momento (ou torque):
M = F.d.sen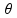
Sendo:
M é o momento ou torque
F é a força exercida
d é a distância entre a força e aonde ela é executada
é o ângulo entre a força e aonde ela está sendo executada
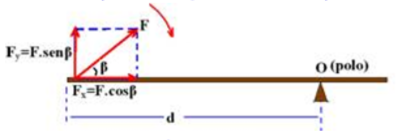
Ao mantermos o momento e o ângulo constantes, como o jardineiro aumentou a distância ao prolongar o cabo, a força, consequentemente, será menor. Alternativa a correta.
06- Calculando o momento de cada força com o polo (eixo de rotação) na posição indicada e estabelecendo o sentido horário de rotação como positivo e anti- horário como negativo:
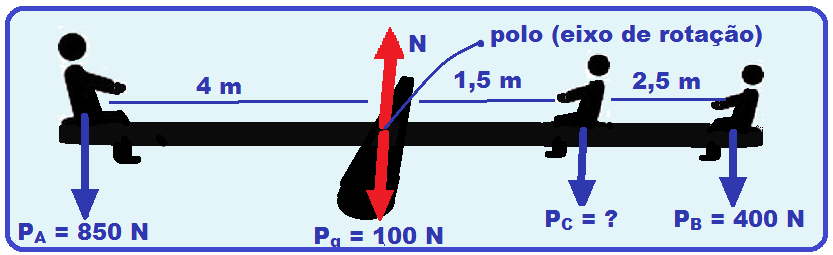
MPA = – 850.4 = – 3400 N.m 
MPG = MN = 0 MPC = + Pc.1,5 MPB = + 400.4 = + 1600 N.m.
No equilíbrio de rotação a soma dos momentos de cada força deve ser nulo – 3400 + 0 + 1,5PC +
1600 = 0 1,5PC = 1800 PC = 
= 1200 N.
PC = mC.g 1200 = mC.10 mC = 120 kg.
R- D
07- Se você não domina a teoria, veja as informações a seguir:
Momento (ou torque) de uma força
O sinal do momento da força pode ser negativo ou positivo e, por convenção, vamos adotar osentido horário de rotação em torno de O como positivo e anti-horário como negativo.
Condições de equilíbrio de um corpo extenso
São duas as condições para que um corpo extenso rígido esteja em equilíbrio:
1a 
Equilíbrio de translação A resultante do sistema de forças deve ser nula.
2a Equilíbrio de rotação A soma algébrica dos momentos das forças que agem sobre o sistema, em relação à qualquer ponto (polo O),deve ser nula.
Resolvendo o sistema composto pelas duas equações acima você chega à resolução do exercício.
No caso do exercício, vamos colocar as forças que agem sobre a barra de intensidades:
Parroz (peso do arroz) 
Pbarrapeso da barra (no meio da barra, pois ela é homogênea) N (reação normal que o apoio aplica na barra)
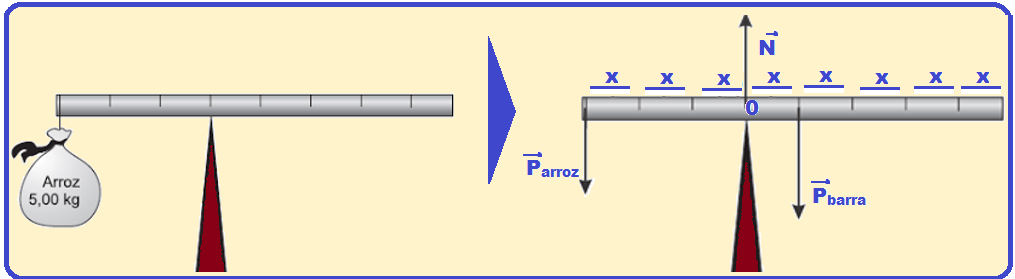
Momento de cada força em relação ao polo 0:
Mbarra = + Pbarra.1x MN = N.0 = 0 Marroz = – Parroz.3x.
Condição de equilíbrio de rotação a soma dos momentos de cada força, em relação ao ponto O, deve ser nula:
Pbarra.1x + 0 – Parroz.3x = 0 mbarra.g= 3.marroz.g marroz = 5,00 kg (veja desenho)
mbarra.g = marroz.g.3 mbarra = 3.5,00 mbarra = 15,00 kg.
R- E
08-
Momento ou torque de uma força
O sinal do momento da força pode ser negativo ou positivo e, por convenção, vamos adotar o sentido horário de rotação em torno de O como positivo e anti-horário como negativo.
São duas as condições para que um corpo extenso rígido esteja em equilíbrio:
1a Equilíbrio de translação A resultante do sistema de forças deve ser nula.
2a Equilíbrio de rotação A soma algébrica dos momentos das forças que agem sobre o sistema, em relação ao ponto de apoio (pólo O),deve ser nula.
