Resoluções – Estática – 2013 e 2014

Estática – 2013 – 2014

RESOLUÇÕES

01- Equilíbrio na vertical — N_A + N_B = P.

Equilíbrio de rotação — a soma dos momentos de cada força em relação ao polo (colocado em A)

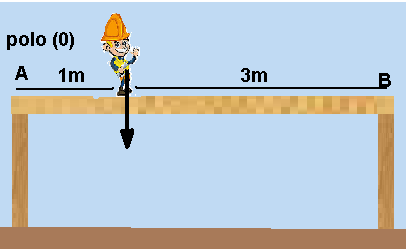
deve ser nula.

M_NA=N_A.0=0 — M_P= + P.1= p — M_NB= – N_B.3= – 3N_B — 0 + P – 3N_B = 0 — N_B = P/3 (I).

N_A + N_B = 3 — N_A + P/3 = P — N_A=P – P/3= (3P – P)/3 N_A=2.(P/3) (II).

Comparando (I) com (II) — N_A = 2 N_B.

R- B

02- A componente do peso (P_p) paralela ao plano inclinado, responsável pela descida do bloco, é fornecida por P_p=PsenӨ=m.g.senӨ=2,8,10,0,8 — P_p=22,4N — intensidade da força de atrito estático máxima (iminência de movimento) é dada por F_at=μN=μPcosӨ=μmgcosӨ — F_at=0,5×2,8x10x0,6 — F_at=8,4N —

a intensidade da força elástica (F_e) é fornecida por F_e=K.x, onde x é de quanto a mola está distendida —

F_e=350.x — essas forças estão colocadas na figura abaixo — como, pelo enunciado, o sistema se

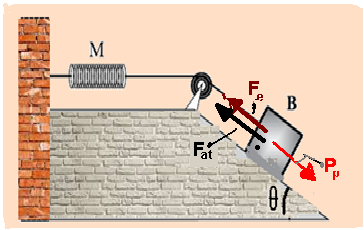
encontra em equilíbrio, a força resultante sobre o bloco é nula (F_R=0) e, assim P_p = F_el + F_at — 22,4 = 350 + 8,4 — 350.x = 14 — x=14/350 — x=0,04m=4,0cm — R- E

03- Teoria: Plano inclinado com atrito 

As forças que agem sobre um corpo apoiado sobre um plano inclinado são seu peso, vertical e para baixo e a força normal , perpendicular à superfície de contato entre o bloco e o plano.

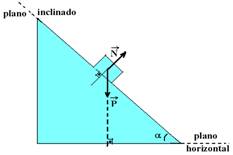
α é o ângulo de inclinação do plano. Como  e  não tem a mesma direção, vamos decompor o peso  em duas parcelas:

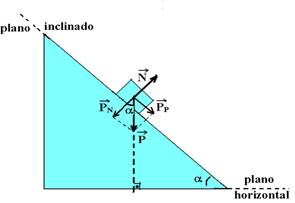
  parcela do peso paralela à superfície do plano inclinado (responsável pela tentativa de descida do bloco).

 parcela do peso perpendicular à superfície do plano inclinado (força que comprime o bloco contra o plano)

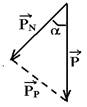
sen α =cateto oposto/hipotenusa  —  sen α =P_P/P  —  P_P=P.senα

cos α =cateto adjacente/hipotenusa  —  cos α =P_N/P  —  P_N=P.cosα

 

As duas forças acima substituem o peso e podemos tirá-lo:

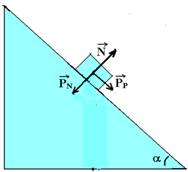
A componente normal do peso  anula a reação normal do apoio , assim temos:

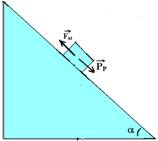
A força de atrito é sempre contrária ao movimento ou à sua tendência e é fornecida por F_at=μN  —  P_N=N  —  F_at=μP_N  — F_at=μPcosa  —  F_at=μmgcosα

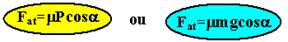
Se o bloco estiver em equilíbrio (estático ou dinâmico), a força resultante sobre ele seria nula e, nesse caso, P_P=F_at .

Para se determinar o coeficiente de atrito estático (F_ate) de um corpo, que é o valor máximo do coeficiente de atrito, devemos colocar esse corpo sobre um plano inclinado e ir aumentando o ângulo até que ele esteja na iminência de movimento e medir esse ângulo.

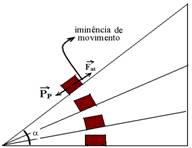
Na iminência de movimento P_P=F_ate  —  Psenα=μePcosα  —  μ_e=sena/cosα  —  μ_e=tgα

N0 caso do exercício — μ_e=tgα=tg30^o = √3/3

R- D

04- Veja a figura abaixo onde foi calculada a soma vetorial pela regra do paralelogramo — aplicando

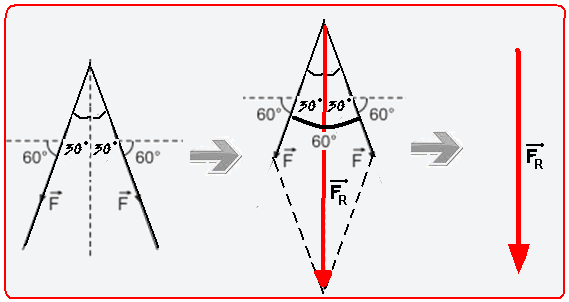
a lei dos cossenos — F_R² = F² + F² + 2.F.F.cos60^o=2F² + 2F².(1/2) — F_R=√(3F²) — F_R=√(3) .F

R- E

05- Na primeira figura estão colocadas as forças e, considerando a prateleira de densidade homogênea o peso e todas as outras forças estão aplicadas no centro (meio) da prateleira e essas forças são:

Peso  — vertical, para baixo e de intensidade P=mg=2.10 — P=20N

Tensão (tração)  no cabo aplicada na prateleira pela parede

Normal  — aplicada pela parede na prateira (horizontal e para a direita)

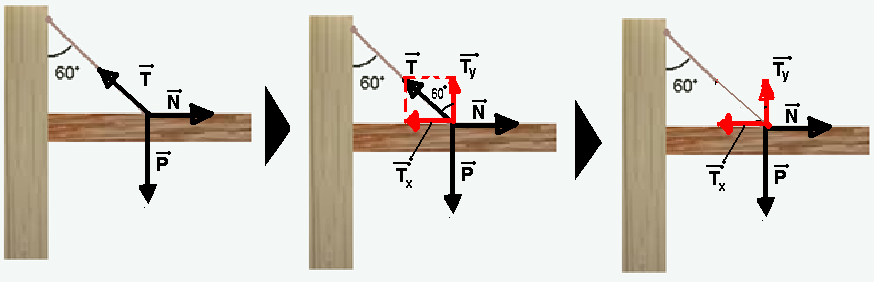
Na segunda figura a tração  foi decomposta em duas parcelas de intensidades T_y=Tcos60^o=0,5T e T_x=Tsen60^o=(√3/2)T.

Na terceira figura, como o sistema está em equilíbrio, na vertical, T_y=P — 0,5T=20 — T=40N.

R- D

Obs: Se fosse pedido a reação normal  aplicada pela parede na prateira você teria que na horizontal também existe equilíbrio e N=F_y=(√3/2)T=(√3/2).40 — N=20√3N

06- Peso de cada esfera — P₁=m₁g=0,3.10 — P₁=3N — P₂=m₂g=0,2.10 — P₂=2N — P₃=m₃g=0,1.10 — P₃=1N

Observe na figura todas as forças que agem sobre cada esfera e, como cada uma está em equilíbrio a força resultante sobre cada uma será nula, então você terá:

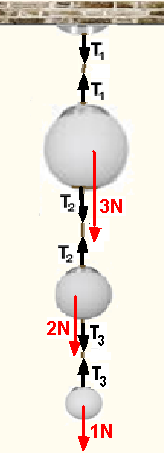
Esfera 3 — T₃=1N — esfera 2 — T₃ + 2 = T₂ — 1 + 2=T₂ — T₂=3N — esfera 1 — T₁ = T₂ + 3 —

T₁=3 + 3 — T₁=6N

R- A

07- Se o peso da criança (II) é duas vezes maior que o da criança (I), a criança (II), para que haja equilíbrio, deve estar a uma distância duas vezes menor que a criança (I) do apoio.

R- C

08- Veja teoria a seguir:

Se você pendurar um quadro na parede por meio de dois fios, quanto menor for o ângulo formado com o teto, ou o suporte, maior será a força de tração (tensão) no fio.

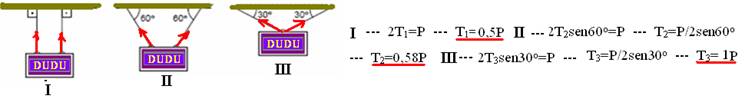
R- A

09-Lei de Hooke — F_e=kx — k=60N/m e no dia de menor rendimento x=0,8m — F_e=60.0,8=48N.

R- E

10-

O1. Correta — possui maior área de contato com o solo oferecendo mais estabilidade para caminhar.

02. Correta — o salto alto desloca o peso e consequentemente o centro de gravidade. Veja figura

abaixo.

04. Falsa — veja 02.

08. Correta — com salto o peso é deslocado para a frente e sem salto, num plano inclinado o peso

também é deslocado para a frente.

16. Falsa — pressão=força (no caso, o peso)/área de contato com o solo) — P=P/S — observe que a pressão P é inversamente proporcional à área de contato — com o sapato B, S é menor, e a pressão sobre o solo é maior.

Soma (01 + 02 + 08)= 11

11- Como os blocos se movem com velocidade constante, estão em MRU e a intensidade da força resultante sobre cada um deles é nula.

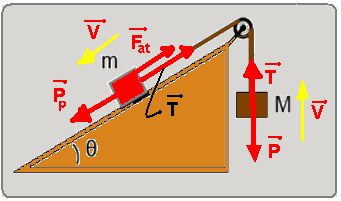
Bloco de massa M — T=P — T=Mg (I)

Bloco de massa m — P_p = T + F_at — mgsenθ = T + μ_cmgcosθ — T=mgsenθ – μ_cmgcosθ (II)

(I) = (II) — Mg = mgsenθ – μ_cmgcosθ — M= msenθ – μ_cmcosθ

R-B

12- Observe as figuras abaixo onde as forças são:

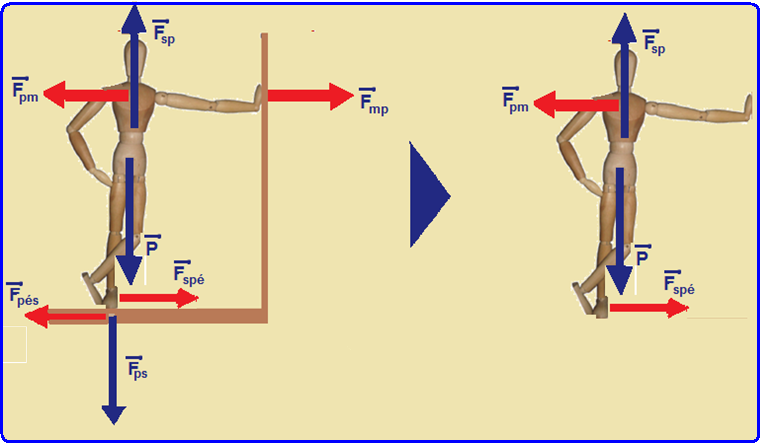
 – força que a mão aplica aplica na parede e  – força com que a parede reage na mão e consequentemente na pessoa.

 – peso da pessoa cuja reação está no centro da Terra.

 – força que a pessoa aplica no solo e  – força com que o solo reage sobre a pessoa (essa força é denominada de força normal )

 – força com que o pé empurra o solo e  força com que o solo reage sobre o pé (essas forças são as força de atrito trocadas entre o pé e o solo).

Na figura da direita estão colocadas apenas as forças que agem sobre o indivíduo e que se anulam na vertical e na horizontal, pois o indivíduo encontra-se em repouso (força resultante nula).

Estática de um ponto material

 

38– Determinando  o valor da constante elástica k da mola pela figura 1  —  quando x=4,0cm=4.10^-2m, F=20N  —  F_e=kx  —  20=k.4.10^-2  —  k=5.10² N/m  —  força aplicada pela mola quando o sistema está em equilíbrio e a mola deformada de x=6,4cm=6,4.10^-2m  —  F=kx=5.10².6,4.10^-2=32N  —  observe a seqüência das figuras abaixo onde

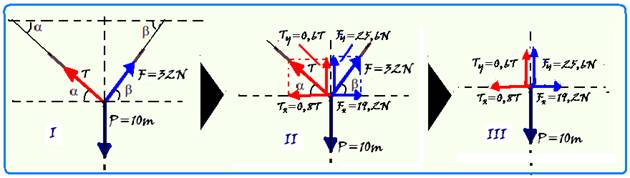
foram colocadas todas as forças no ponto de interseção dos fios (I)  —  em (II) foram decompostas as forças inclinadas  —  T_x=Tcosα=0,8T  —  T_y=Tsenα=0,6T  —  F_x=Fcosβ=32.0,6=19,2N  —  F_y=Fsenβ=32.0,8=25,6N  —  em (III) estão colocadas apenas as forças que agem nas direções horizontal e vertical  —  estando o sistema em equilíbrio essas forças se anulam em cada direção  —  na horizontal  —  0,8T=19,2  —  T=24N  —  na vertical  —  0,6T + 25,6 = 10m  — 

0,6.24 + 25,6 = 10m  —  14,4 + 25,6 = 10m  —  m=40/10=4kg  —  R- C.

 

Corpo extenso – centro de massa e tipos de equilíbrio

 

 21- Com duas pessoas no carro a deformação do sistema de molas é x=2cm=2.10^-2m e  a força que deformadora é o peso das duas pessoas  —  P=2mg=2.60.10=12.10²N  —  esse peso corresponde à força elástica  —  F_eP=kx  — 

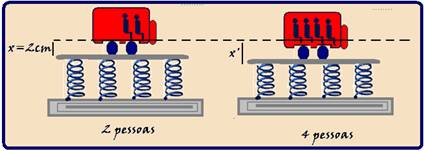
12.10²=k.2.10^-2  —  k=6.10⁴N/m (constante elástica do sistema de molas que é constante independente da força deformadora)  —  com  4 pessoas a deformação é x’ e o peso é P’=4mg=4.70.10=28.10²N  —   P’=kx’  —  28.10²=6.10⁴x’  —  x’=4,66.10^-2m=4,66cm  —  R- D.

 

22- Leia a teoria abaixo:

Associação de polias ou roldanas

a) Uma polia fixa e outra móvel

A polia de cima, fixa, não interfere no valor da força aplicada pela pessoa, serve apenas para sua comodidade, levantando o bloco ao puxar o fio para baixo.

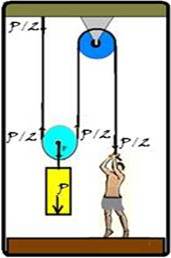
A polia de baixo, móvel, reduz à metade a força aplicada pela pessoa (metade do peso do bloco). Lembre-se de que, se a pessoa puxar o fio de uma distancia d, o bloco subirá d/2.

 b) Uma polia fixa e várias polias móveis (talha exponencial)

Na figura abaixo, onde temos 3 polias móveis e uma fixa, o bloco de peso P é mantido em equilíbrio pela pessoa. Observe que

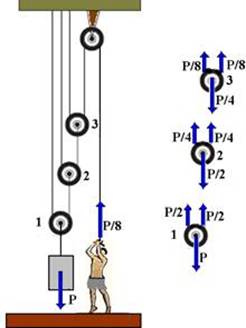
a força que a pessoas aplica tem intensidade 8 vezes menor que o peso do bloco e que cada polia móvel reduz pela metade a força aplicada nela. Esse tipo de associação é chamado de talha exponencial e a força exercida pela pessoa, se tivermos n polias móveis, corresponde a 2n do peso do bloco com n=1,2,3… .

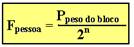
Assim, se o bloco da figura acima tiver peso de 80N, a pessoa deve fazer uma força de apenas 10N para mantê-lo em equilíbrio, mas, se ele puxar a corda de 1m, o bloco subirá apenas 0,125m (8 vezes menor).

Observe na figura do exercício que existem duas polias móveis  —  F=P/2²=P/4  —  R- D.

 

Estática de um corpo extenso – máquinas simples

 

66- Trata-se de uma alavanca interfixa – o apoio está entre a força potente e a força resistente  —  observe a alavanca

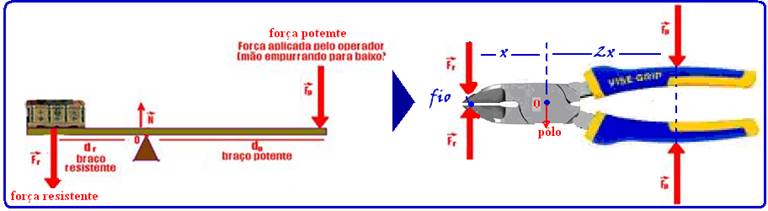
 interfixa acima  —  havendo equilíbrio, a soma dos momentos das forças em relação ao apoio deve ser nula  —  F_o.2x=Fr.x­  ­—  F_r/F_o=2x/x­  —  F_r=2F_p  —  observe que quanto maior for o braço potente, maior será a vantagem mecânica, ou seja, maior será a força transmitida  —  R- A.

67- O exercício quer o diagrama das forças que as dobradiças aplicam na porta:

Na horizontal: ao girar, a porta traciona  (puxa) para a direita a dobradiça superior e esta, pelo princípio da ação e reação reage na porta com uma força de mesma intensidade, mesma direção, mas sentido contrário, tracionando-a (puxando-a) para a esquerda com uma força   —  analogamente ao girar, a porta comprime  (empurra) para a esquerda a dobradiça superior e esta, pelo princípio da ação e reação reage na porta com uma força de mesma intensidade, mesma direção mas sentido contrário, comprimindo-a (empurrando-a) para a direita com uma força _. 

Na vertical, devido ao seu peso, a porta aplica em cada dobradiça uma força puxando-as para baixo e, elas reagem sobre a porta com forças  e , verticais e para cima.

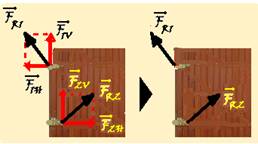
A soma vetorial dessas forças, fornece as forças resultantes  e que cada dobradiça exerce sobre a porta (figura)  R- D.

68- Peso do chumbo quadrado  —  P=m.g=0,030×10=0,3N  —  peso dos triângulos de chumbo  —  P=m.9=0,010×10=0,1N  —  colocando as forças na haste maior e considerando o ponto O como pólo (figura)  —  equilíbrio de rotação  —  a soma dos momentos de cada força em relação ao pólo O deve ser nula  —  M_0,3N= – F,d = –

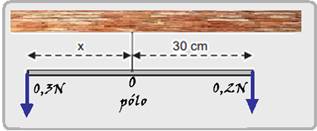
0,3.x  —  M_0,2N = + F.d=+0,2.30 =6N.cm  —  M_0,3N + M_0,2N=0  —  – 0,3x + 6=0  —  x=6/0,3  —  x=20cm  —    R- C.

69– Se você chamar as reações em A e B de N_A e N_B, a reação de contato da esfera Q na barra de P_Q, e considerar o 

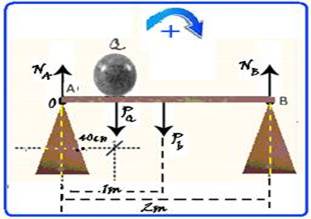
peso da barra (P_b) atuando no centro geométrico da mesma, aplicando a condições de equilíbrio de rotação: somatório de momentos em relação ao ponto A (pólo) igual a zero, você terá  —   M_NA=N_A.d=0  —  M_pQ=+P_Q.d=+80.0,4=32N.m  —  M_Pb=+P_b.d  — M_Pb=50.1=50N.m  —  M_NB=- N_B.d=-N_B.2  — 0 + 32 + 50 – 2N_B = 0  —  N_B=82/2  —  N_B=41N  —  R- B.  

70– Peso do homem  —  P_H=m.g=80.10=800N  —  cálculo do momento de cada força colocando o polo (eixo

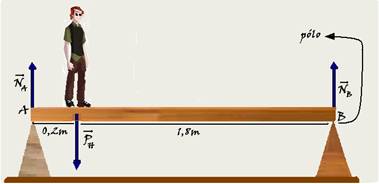
de rotação) em B  —  N_NA=N_A.d_AB=2N_A  —  M_PH= – P_H.d_HB= – 800.1,8= – 1440N.m  —  M_NB=N_B.d=N_B.0=0  —  equilíbrio de rotação  —  a soma dos momentos de cada força em relação ao pólo é nula  —  2N_A – 1440 + 0 = 0  —  N_A=1440/2  —  N_A=720 N  —  R- D.

71- Projetando as forças e as distâncias nas direções perpendiculares à viga  —  em (I), forças  —  cos60^o=F/80  —  1/2 =

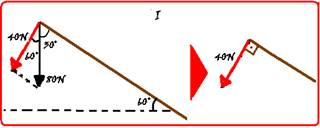
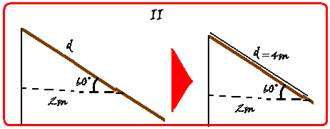
F/80  —  2F=80  —  F=40N  —  em (II), distâncias  —  cos60^o=2/d  —  1/2 = 2/d  —  d=4m  —  veja na figura (III) como fica o esquema pronto para você calcular o momento de cada força com o pólo em A  —  M_PE= – 40.16= – 640

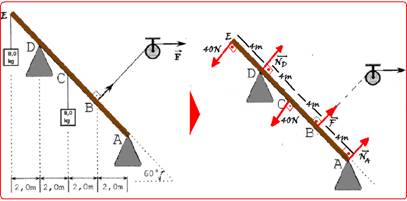
 N.m  —  M_NB= + N_Dx12  —  M_PC= – 40.8= – 320N  —  M_F= + 30.4  —  M_NA=N_A.0=0  —  a soma dos momentos de cada força deve ser nula  —  -640 +12N_D – 320 +120 + 0=0  —  12N_D=840  —  N_D=70N  —  R- C.

Voltar para os exercícios