Resolução Dinâmica
Resoluções-Vestibulares Recentes por assunto
2017, 2016 e 2015
APLICAÇÕES DAS TRÊS LEIS DE NEWTON
01-Nesse caso o objeto tem uma velocidade constante, logo sua aceleração é 0. Como sua aceleração é 0, a força resultante também só pode ser 0, com isso a alternativa correta é a D.
Vamos analisar as outras, também:
A velocidade tem sempre a mesma direção e sentido da força resultante, pois ela é uma consequência da aceleração que vai ser exercida por essa força.
Se a resultante fosse igual ao peso, o objeto estaria em queda livre.
A alternativa C pode causar confusão, porque realmente ela é verdadeira, mas no caso aonde há uma força resultante.
Sempre há forças agindo, porém a soma delas vai ser igual a 0.
R – D
02-
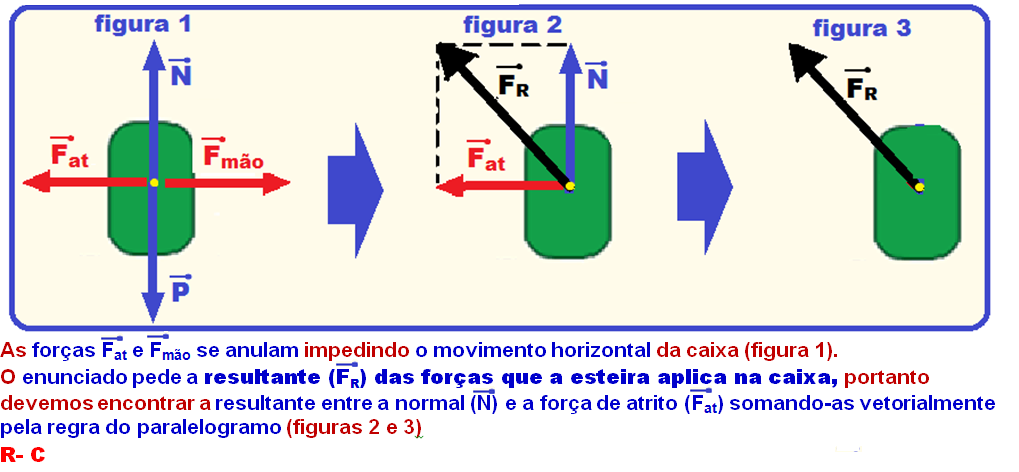
03-Denominando de ml a massa de cada cubo laranja e de ma a massa de cada cubo azul e, estando as balanças em equilíbrio, você terá:
Balança da esquerda
2ma + ml = 2 (I)
Balança da direita ma + 3 = 2ml (II)
Isolando ma em (II) e substituindo em (I) ma = 2ml – 3 2(2ml – 3) + ml = 2 4ml – 6 + ml = 2 5ml = 8 ml= 8/5 = 1,6 kg.
2ma + 1,6 =2 ma = 0,4/2 ma = 0,2 kg.
Assim, a massa de um cubo laranja supera a de um cubo azul em ml – ma= 1,6 – 0,2 = 1,4 kg.
R- D
04-
05-a) Em todo gráfico Vxt o deslocamento 
do corpo é numericamente igual á área, nesse caso, entre os instantes 0 e 10 s que é a área de um trapézio:
Mas, o enunciado não pede o deslocamento entre 0s e 10s, mas sim aposição no instante t = 10 s
e, pelo gráfico Sxt você observa que ele partiu da origem So = 0, entãoquando t = 10s o espaço S será 
= S – So 26 = S – 0 S = 26 m.
b) Observe no gráfico da velocidade que, entre 5s e 10 s o gráfico é uma mesma reta inclinada o que significa que nesse intervalo de tempo a aceleração tem o mesmo módulo que pode ser calculado por a = 
= 
a = – 
em módulo a = 0,8 m/s2.
Pelo Princípio Fundamental da Dinâmica ou Segunda lei de Newton FR= m.a = 8.0,8
FR = 6,4 N.
06- Dados: massa do reboque 
m = 16.103 kg aceleração do reboque a = 200 cm/s2 = 200.10-2 m/s2 a = 2 m/s2.
07-No início, quando ele sobe acelerando, a força exercida pelo cabo na cabine tem intensidade maior que a do peso, pois a força resultante é para cima FI > P.
No final, antes da parada, ele está freando e desacelerando com a força resultante sendo para cima até se tornar nula quando FF = P (ele para)
R- B
08-
09-
R- C
10-Se a velocidade de queda é constante, ele deverá percorrer distâncias iguais em intervalos de tempo iguais.
R- D
FORÇA ELÁSTICA
01-a) Observe na figura abaixo que, depois que o objeto foi preso à mola que estava em seu comprimento natural de 20cm, ela foi deformada com seu comprimento passando para 25cm e
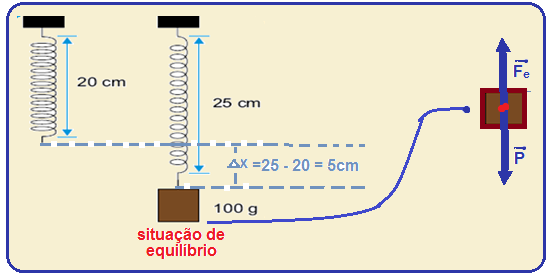
sofrendo uma deformação de ∆x = 5cm = 0,05m, quando atingiu a situação de equilíbrio.
Na situação de equilíbrio, as forças que agem sobre o objeto são, seu peso (vertical e para baixo) e a força elástica (vertical e para cima), que sustenta o objeto, que está em equilíbrio, mas não em repouso (força resultante sobre ele é nula).
b) Suponha que o objeto seja elevado até a altura em que o comprimento da mola volta a ser 20 cm e, em seguida, solto a partir do repouso. Determine a energia cinética do objeto, em joules, no instante em que passa pelo ponto em que o comprimento da mola é de 25 cm. Despreze qualquer perda de energia mecânica.
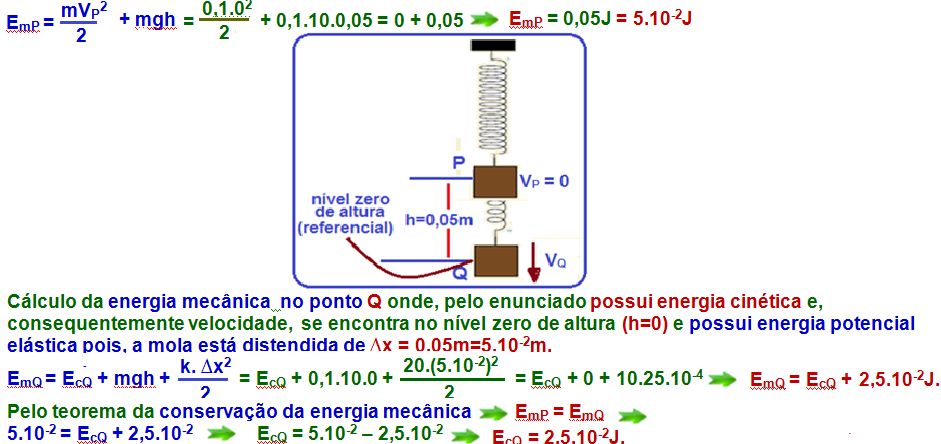
b) Cálculo da energia mecânica no ponto P onde, pelo enunciado partiu do repouso VP = 0 e se encontra na altura de h=0,05m em relação ao ponto Q tomado como referencial. Nesse ponto, a mola está em sua posição natural e não existe energia potencial elástica armazenada.
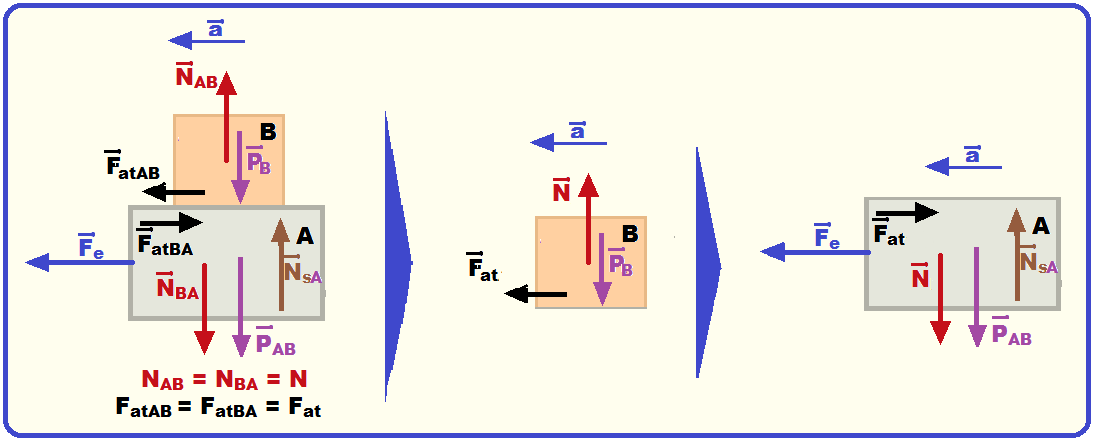
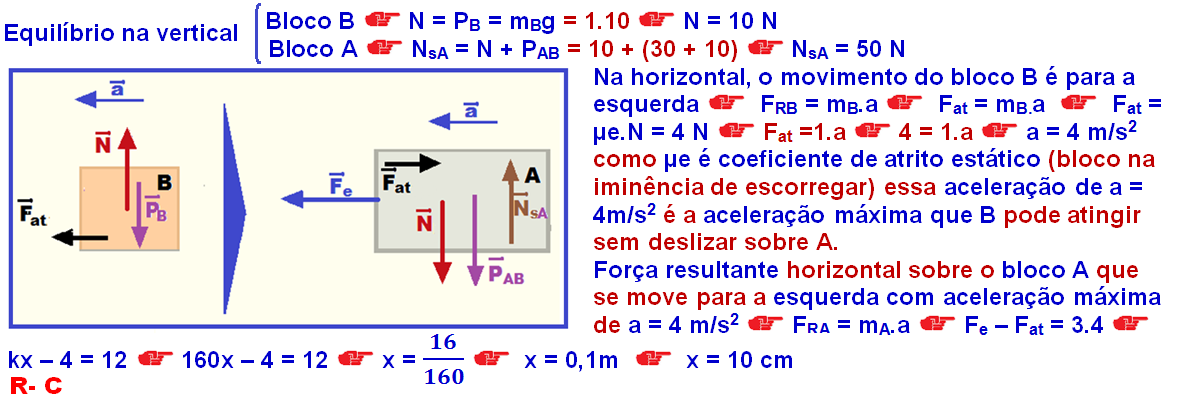
02- Forças que agem sobre cada bloco supondo que a mola está sendo esticada e, quando solta, se moverá para a esquerda:
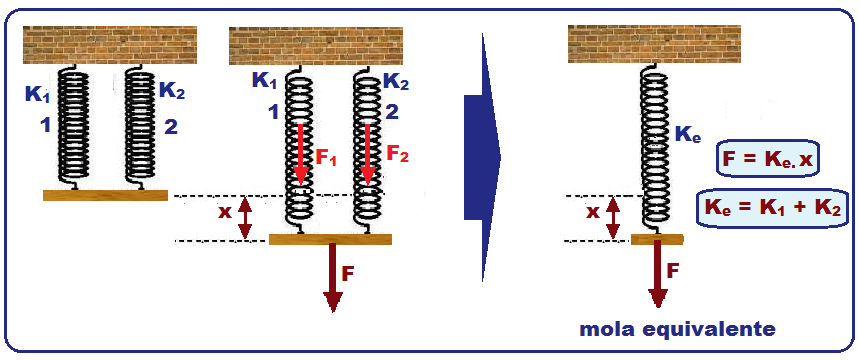
03-Veja as características das associações série e paralelo de molas abaixo:
Associação em paralelo
Nesse caso a deformação x sofrida por cada uma das molas é a mesma.
Associação em série
Nesse caso as molas 1 e 2 estão sujeitas à mesma força F e sofrem deformações diferentes x1 e x2.
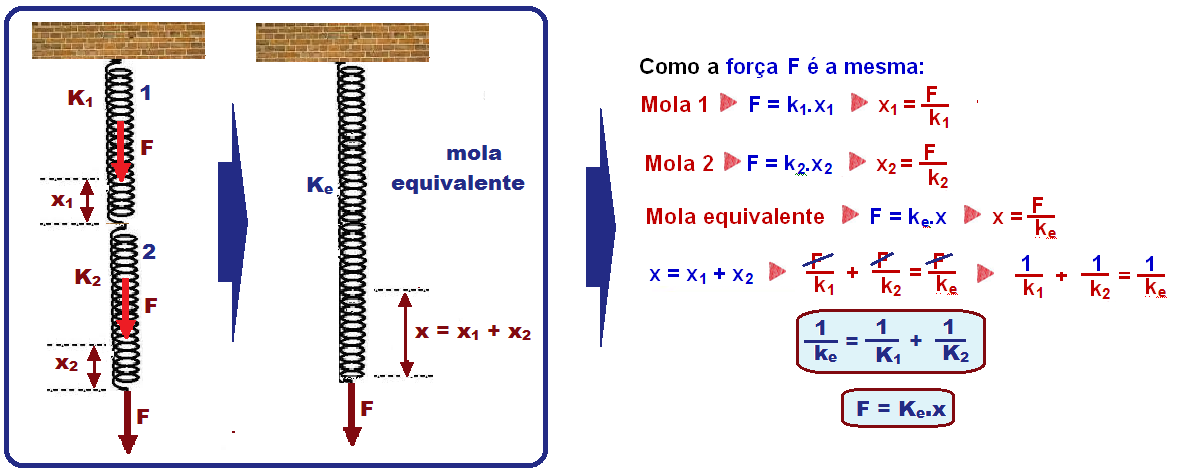
Observe que a constante elástica (coeficiente elástico) da associação paralelo é maior do que a da série.
R- B
04-
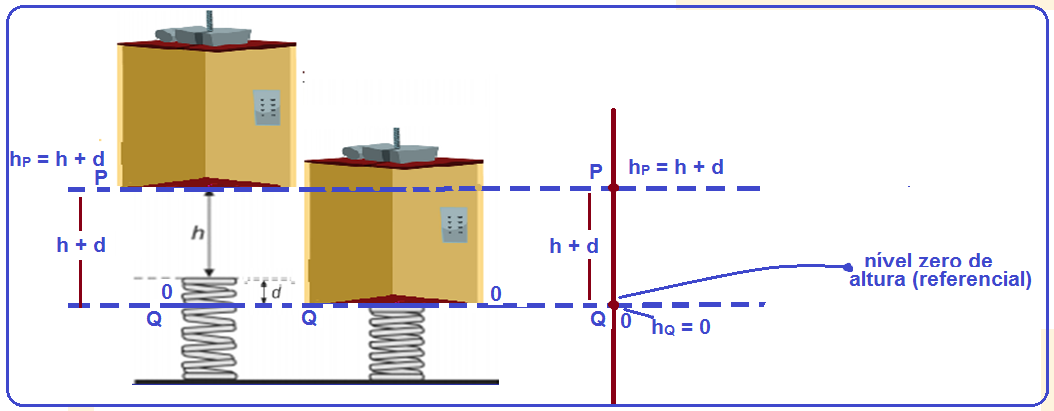
05-Podemos descrever a situação conforme o esquema abaixo:
R- C
06-A expressão da frequência de oscilação de um sistema massa mola é 
(se você não domina a teoria, a demonstração está em fisicaevestibular.com.br – mecânica – dinâmica – MHS – sistema massa-mola).
R- C
PÊNDULOS SIMPLES
01-
Pêndulo Simples
Pêndulo Simples 
consta de uma massa m, presa na extremidade inferior de um fio ideal, fixada verticalmente na sua extremidade superior (figura) .
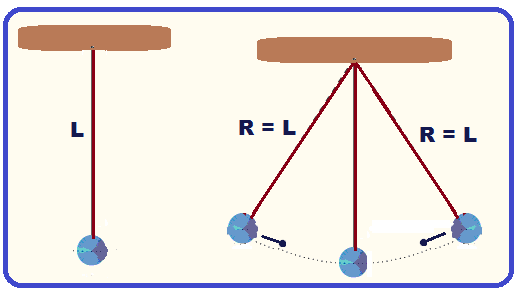
Se o pêndulo simples oscilar, com oscilações de pequena abertura (no máximo 15o), ele descreve um movimento circular de raio R=L, sendo L o comprimento do fio.
Seu período (T), que é o tempo que ele demora para efetuar um “vai e vem” completo é fornecido pela expressão:
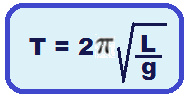
onde g é a aceleração da gravidade local.
Observe na figura abaixo a sequência da situação descrita desde to = 0 até a esfera efetuar uma oscilação completa com período T.
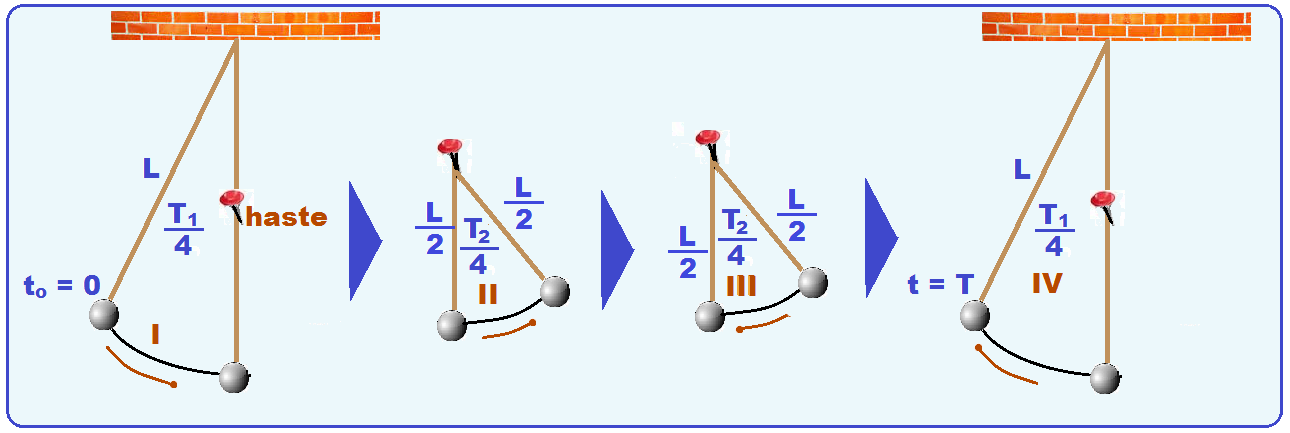
R- E
02-Pêndulo Simples: consta de uma massa m, presa na extremidade inferior de um fio ideal, fixada verticalmente na sua extremidade superior(figura)
Se o pêndulo simples oscilar, com oscilações de pequena abertura (no máximo 15o), ele descreve um movimento circular de raio R=L, sendo L o comprimento do fio.
Seu período (T), que é o tempo que ele demora para efetuar um “vai e vem” completo é fornecido pela expressão:
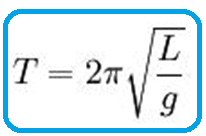
onde g é a aceleração da gravidade local.
Observe que:
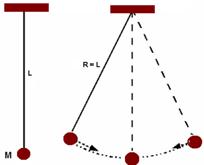
* a massa pendular m não influi no período T do movimento influindo apenas o comprimento L do pêndulo, e a aceleração da gravidade local.Assim, dois pêndulos de mesmo comprimento L, mas de massas diferentes M e m, apresentam o mesmo período T.
* O período de um pêndulo simples independe da amplitude, ou seja, daaltura em que m é abandonada, assim, os pêndulos da figura abaixo, tanto na situação 1 como na 2, demoram o mesmo tempo para ir de A até B, de B até C, de C até B e de B até A.
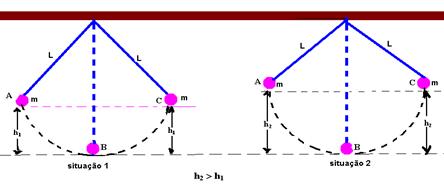
R- A
PLANO INCLINADO
01-
As duas esferas possuem a mesma massa e são abandonadas do repouso da mesma altura h.
A esfera A cai em queda livre sujeita apenas ao seu peso de intensidade P = m.g que é a força resultante sobre ele de modo que FR = m.aA 
FR = P m.aA = m.g aA = g (I)
R- E
02-
03-
Plano inclinado com atrito
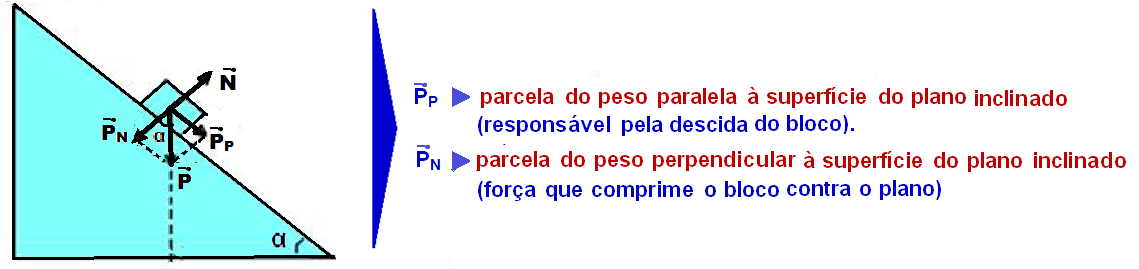
Cálculo da intensidade de PP e PN utilizando o triângulo retângulo da figura abaixo:
P
No caso do exercício no trecho BC existe atrito com o Fat valendo Fat = 
mgcos30o.= 
.mg 
Fat = 
.
No trecho com atrito sen30o = h2/BC 
= h2/BC BC = 2h2
Energia dissipada pelo atrito no trecho BC WFat = Fat.BC.cos30o = .2h2
WFat = 
.h2.
Energia mecânica no ponto A EmA = EcA + EpA = mVA2/2 + mg(h1 + h2) = 0 + mg(h1 + h2) EmA =mg.(h1 + h2).
Energia mecânica no ponto C onde, pelo enunciado, chega com velocidade nula EmC = mVC2/2 + mgh = m.02/2 + mg.0 EmC = 0.
Pelo teorema da conservação da energia mecânica EmA = WFat + EmC mg.(h1 + h2) = .h2 + 0 (h1 + h2)/h2 = 
h1/h2 + 1 = h1/h2 = – 1 = (3-2)/2 h1/h2 =
R- A
04 
05-
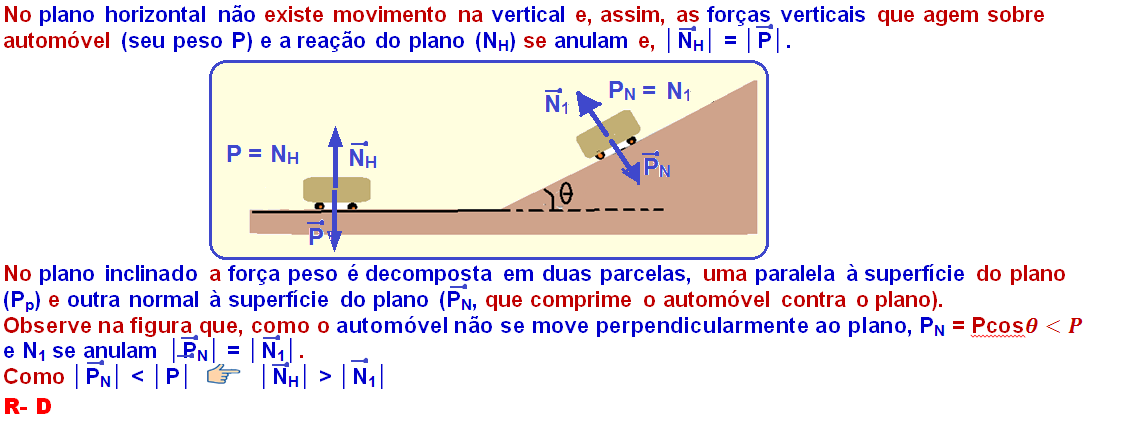
POLIAS E ROLDANAS
01-Cálculo da intensidade da força
necessária para deixar o navio na iminência do escorregamento que deve ser maior que o módulo da força de atrito estático máxima
No caso do exercício, sendo a praia horizontal N = P
Fate = 
e.N = e.P = e.mg = 0,8x3000x10
Fate = 24000 N.
A intensidade da força de tração 
que puxa o navio tem que ser maior que 24000 N T > 24000 N.
Analise a teoria abaixo com uma polia fixa e várias polias móveis (talha exponencial):
02-
Vamos analisar as forças desse exercício:
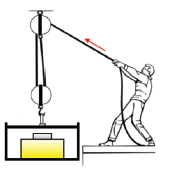
A seta vermelha representa a força resultante, a azul representa a força que a caixa inferior exerce na superior (precisamos descobrir o valor) e averde a força que a superior exerce na inferior. A força resultante deve ser igual à soma das outras forças, então:
Onde:
FR é a força resultante (vermelho)
FI é a força da inferior (azul)
FS é a força do superior (verde)
Como as forças estão em direções opostas, precisamos que uma seja negativa, para facilitar vamos escolher FI, porque ela está em direção oposta em relação à resultante, então:
Isolando FI:
Nesse caso FS é apenas a força peso da caixa superior, nós já temos ela no enunciado (300 N). A força resultante é:
Aonde:
FR é a força resultante
m é a massa
a é aceleração
No entanto nós não sabemos a massa do bloco superior, podemosdescobrir utilizando a força peso:
Aonde:
P é o peso
m é a massa
g é a aceleração da gravidade
Isolando a massa:
Substituindo:
Substituindo na equação da força resultante, a massa é apenas do bloco superior, porque estudamos as reações que acontecem apenas nele:
Agora que temos tudo, podemos substituir para chegarmos ao resultado:
(resposta da a)
Essa é a resposta para o exercício a.
Para o b nós teremos que fazer exatamente as mesmas contas, mas dessa vez o peso será a soma de ambas as caixas e força é a que o piso exerce na caixa inferior:
A relação entre as forças ainda pode ser escrita dessa forma, porém o peso que antes era apenas 300, agora é 300 + 500 = 800 N.
Calculando a massa da caixa inferior:
Substituindo:
Sendo assim a resultante fica:
Substituindo:
(resposta da b)
03-
01 
Verdadeiro 
pelo fato de o sistema ser constituído por duas roldanas acontece o seguinte equilíbrio de forças:
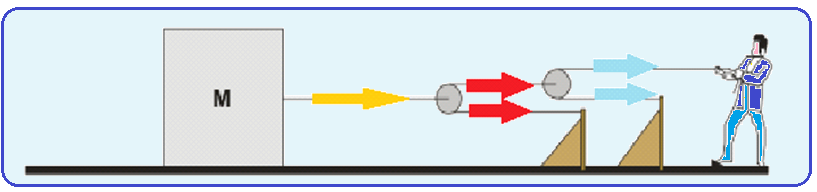
Onde as setas de mesma cor têm a mesma intensidade.
A seta azul representa a força exercida pelo professor (350N). Por ser umaroldana e pelas propriedades de ação e reação uma outra força igual e de mesma direção é aplicada no outro fio.
A soma dessas duas forças resulta na força representada pela seta vermelha, que terá intensidade de 350 + 350 = 700N.
O mesmo raciocínio é válido para se calcular a força representada pela seta amarela, só que nesse caso com forças de 700N, ou seja, 700 + 700 = 1400N.
A seta vermelha é a força normal, que nesse caso tem mesma intensidade da força peso, já que possuem sentidos opostos e não existem outras forças agindo verticalmente no bloco:
N = P N = 4000N.
A seta amarela é a tração, calculada no (01), logo tem intensidade de F=1400N.
A seta verde representa a força de atrito, nesse caso estudaremos o movimento, portanto deveremos considerar o coeficiente de atrito cinético (μc = 0,25). A força de atrito cinético (Fc) pode ser calculada por Fc = N.μc Fc = 4000.0,25 Fc = 1000N.
Essa força terá sentido para a direita, pois a soma das forças exercidas horizontalmente no lado direito do corpo terão maior intensidade que as do esquerdo. A intensidade dessa força pode ser calculada por Fr = F – Fc Fr = 1400 – 1000 Fr = 400 N.
04 Falso Como estudado no item anterior (02), existe uma outra força além das citadas, a força normal, que surge do contato entre o corpo e o chão.
08 Verdadeiro Também demonstrado no item (02), a força resultante é de 400N.
16 Falso Nesse caso vamos estudar o objeto antes do movimento, com isso utilizaremos o coeficiente de atrito estático (μe), a força exercida para que o bloco se movimente deve ser maior que a força de atrito estático (Fe), calculada a seguir Fe = N.μe Fe = 4000.0.3
Fe = 1200 N.
FORÇAS NO MCU
01-Veja a teoria abaixo que está relacionada com o exercício onde o avião (ou o piloto) comportam-se como a moto e a normal 
que a moto troca com o piso do globo pela força que o avião troca com o ar.
Globo da morte
Suponha um motociclista de massa total m (massa dele + massa da moto) descrevendo voltas segundo um plano vertical, com velocidade escalar constante 
no interior de uma esfera metálica oca de raio R “globo da morte”.
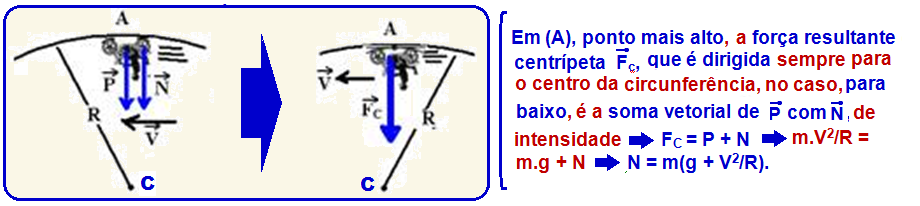
02-Quando a corda atinge a tensão máxima no ponto A (figura), a ela se rompe e a partícula com velocidade VA sai pela tangente e executa um lançamento horizontal com velocidade VA, com trajetória parabólica até atingir o solo percorrendo a distância horizontal 4R e vertical 2R.
Decompõe-se o movimento horizontal em duas parcelas:
Segundo o eixo Y 
trata-se de um movimento uniformemente variado com velocidade inicial Voy = 0, ou seja, é uma queda livre com o corpo abandonado da origem, sujeito
apenas à aceleração da gravidade, de intensidade g, direção vertical e sentido para baixo.
Equações:
S = So + Vo.t + at2/2 Y= 0 + 0.t + gt2/2 Y = g.t2/2
Vy = Voy + a.t Vy= 0 + g.t Vy = g.t
Na vertical, a partícula em queda livre, sai do ponto A com Vo = 0 e percorre a distância vertical Y =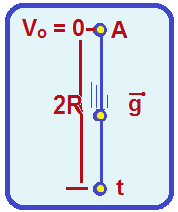
2R até chegar ao solo e demora um tempo t, tal que Y = g.t2/2 2R = g.
t2 =
t = 2
(tempo de queda na vertical que é o mesmo tempo que apartícula demora para percorrer a distância d = 4R na horizontal)
Segundo o eixo X trata-se de um movimento horizontal uniforme comvelocidade constante de intensidade VA , que é a velocidade de lançamento S = So + V.t X= 0 + VA.t X = VA.t.
O tempo t que ela demora para percorrer x = 4R na horizontal é o mesmo que demorou na queda livre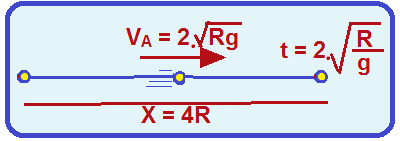
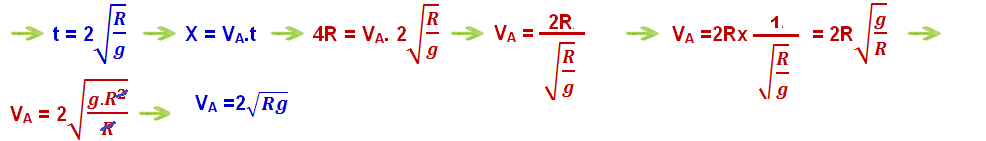
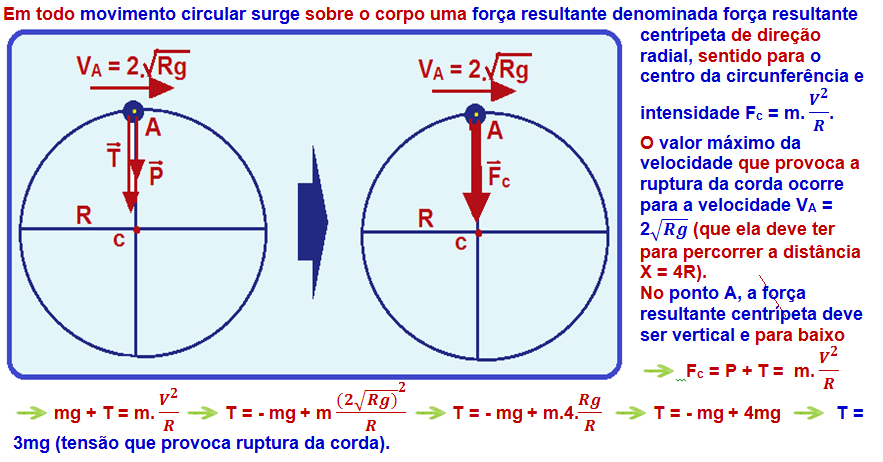R – C
03-
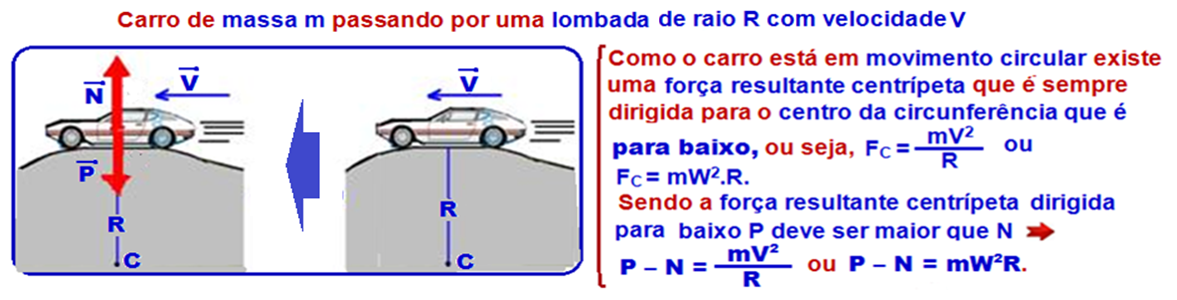
P – N = 
como a força exercida pela pista sobre o carro tem intensidade N tal que – N = – P N = Mg – .
R- B
TRABALHO E ENERGIA
01-
Cálculo da potência teórica (Pt) de cada usina (unidade geradora) que leva em conta a altura (h) da massa m de água represada pela barragem, a gravidade local (g = 10 m/s2) e a densidade da água (da= 1 000 kg/m3) 
Pt = W (energia potencial gravitacional armazenada pela massa m de água na
Sendo a vazão nominal da água de Z = 690 m3/s = Volume/intervalo de tempo (1 s) Z = V/∆t
690 = V/1 V = 690 m3 (volume de água que cai em cada 1s).
dágua = 
1000 = 
m =69.104 kg (massa de água).
Energia potencial gravitacional liberada por m = 69.104 kg de água numaaltura de h = 118,4 m num local onde g = 10 m/s2 W = m.g.h= 69.104.10.118,4 = 8169,6.105 = 816,96.106 J.
Potência teórica (Pt) de cada usina (unidade geradora) Pt = 
=
Pt =816,96.106 W
Pt = 816,96 MW (potência teórica).
Potência não aproveitada em cada unidade geradora de Itaipu = potência teórica – potência instalada
Pperdida= 816,96MW – 700MW Pperdida = 116,96 MW
R – C
02-
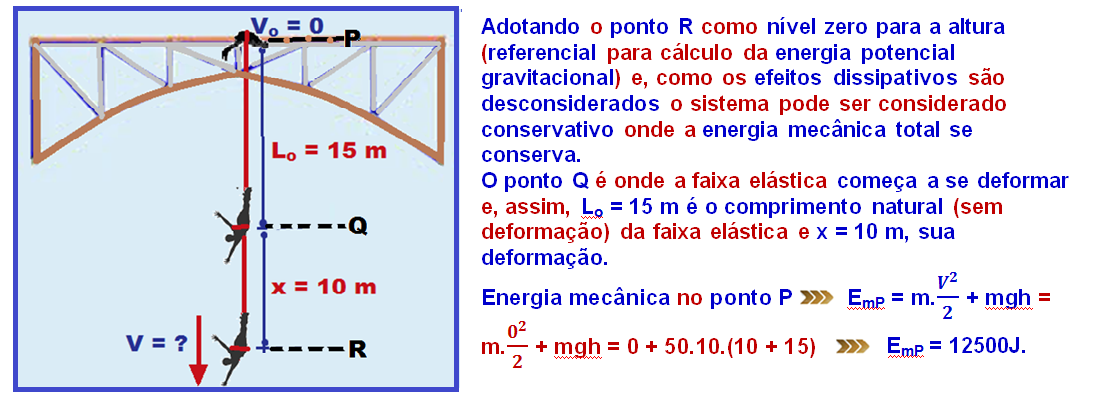
Energia mecânica no ponto R onde a mola está deformada de x = 10 m, h= 0 e o corpo tem velocidade V 
EmR = m.
+ mgh + k.
EmR = 50. + 50.10.0 + 250.
EmR = 25.V2 + 0 + 125.100 EmR = 25.V2+12500.
Sistema conservativo EmP = EmR 12500 = 25.V2 +12500 25V2 = 0 V = 0 e este é o ponto onde a deformação da mola é máxima.
R – A
03-Como em qualquer choque a quantidade de movimento é conservada, já podemos excluir algumas alternativas. Agora só falta resolvermos o problema da energia cinética, o texto deixa bem claro que as velocidades não mudam, antes e depois do choque, como a massa também se mantém, podemos concluir que a energia cinética não muda, portanto, a alternativa E é a correta.
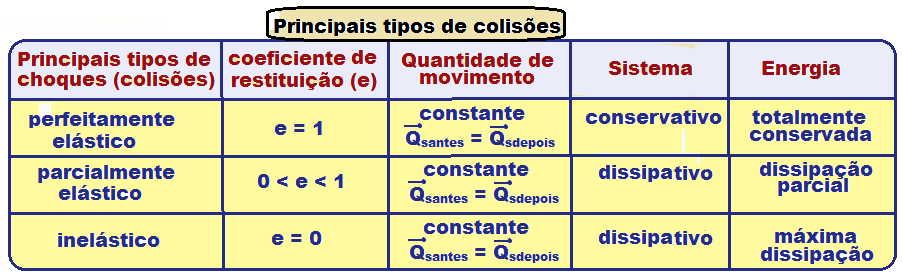
R – E
04-a) Considerando o sistema “projétil, saco de areia e carrinho” isolado de forças externasvocê pode aplicar o teorema da conservação da quantidade de movimento.
Qsa = Qsd 
10 = 1,6 + 100 V V = 
V = 8,4.10-2 m/s
b)
Teorema da energia cinética:
“ O trabalho da resultante de todas as forças que agem sobre um corpo é igual à variação da energia cinética sofrida pelo corpo “
WFR = ∆Ec = Ecd – Eca = mp.(Vpd)2/2 – mp.(Vpa)2/2 WFR = 20.10-3 .802/ 2 – 20.10-3 .5002/ 2 = 64 – 2500 WFR = – 2435 J (o sinal negativo significa que a energia cinética do projétil foi dissipada).
05-Pelo enunciado o aproveitamento da energia eólica ocorre por meio da conversão da energia cinética (Ec) de translação em energia cinética de rotação.
A análise das turbinas eólicas é complexa porque envolve aerodinâmica e mecânica dos fluidos.
Contudo, os conceitos básicos podem ser obtidos a partir de simplificações na análise.
A energia contida no vento horizontal é basicamente sua energia cinética, uma vez que não há variação de pressão, variação de altitude, e, pelo enunciado, a densidade do ar permanece constante o que implica que amassa de ar m que atravessa os permanece constante.
A energia cinética é uma grandeza escalar, não tem direção nem sentido,apenas intensidade, fornecida pela expressão:.
R- B
06-
Propriedade do gráfico forçaxdeslocamento
Em todo gráfico da força F em função do deslocamento d, o trabalho realizado pela força F é numericamente igual à área compreendida entre a reta representativa (linha cheia) e o eixo do deslocamento.
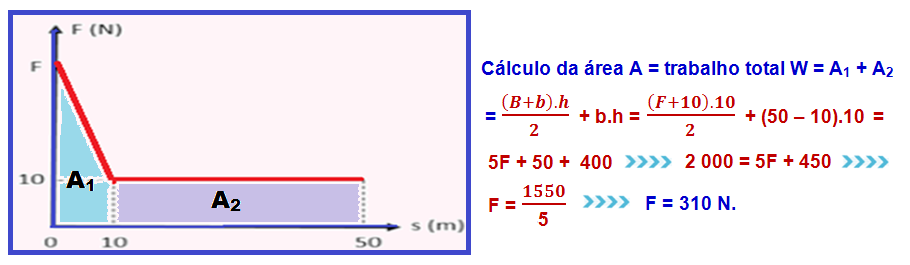
Se, ao final desse deslocamento de d= 50 m a intensidade dessa força F (suposta resultante) fosse mantida constante (F = 310 N), o trabalho realizado por ela seria 
W = F.d = 310.50
W = 15 500 J.
Supondo que essa força F seja a força resultante você pode aplicar o teorema do Trabalho como variação da energia cinética:
WF = Ecf – Eci = Ecf – mVo2/2 = mV2/2 – m02/2 = Ecf – 0 Ecf = 15 500 J.
R- C
07-
08- Observe na figura a que a força 
é decomposta em duas parcelas 
e
e que a parcela responsável pela realização do trabalho no deslocamento é Fx tal que Fx < F.
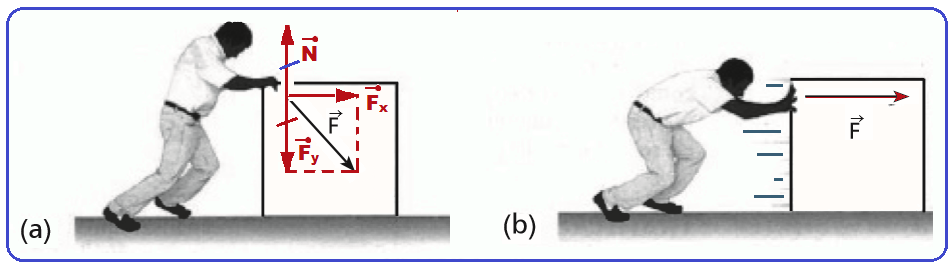
Em b a força que age no deslocamento é .
Como o trabalho em a vale Wa =Fx.d e em b vale, Wb = F.d Wa < Wb.
R- C
09-
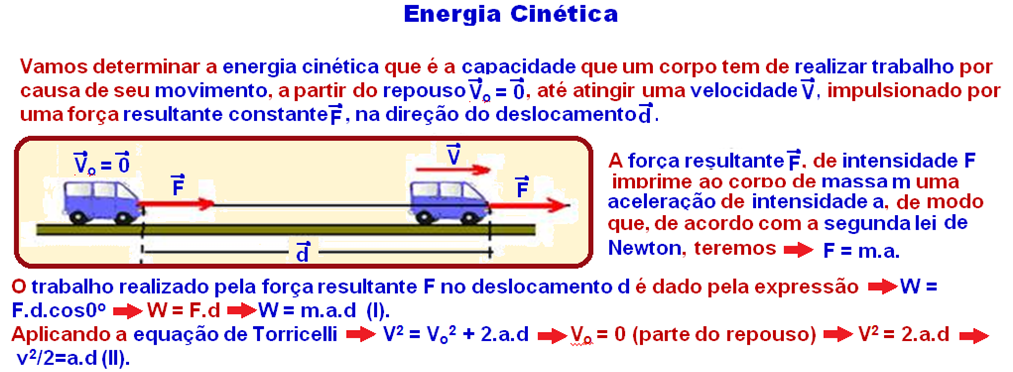
Essa é a expressão da energia cinética de um corpo de massa m no instante em que ele possuivelocidade de
intensidade V
No caso do exercício:
Massa do navio mnavio = 450.000 kg 
massa das pessoas mpessoas = 1000×70 = 70.000 kg
Massa dos carros mcarros = 150×1000 = 150.000 kg.
Massa total do sistema 
= 450000 + 70000 + 150000 =
670.000 kg.
301,5 MJ
10- O enunciado afirma que a esfera está em repouso na posição x = x1 o que implica que, nessa posição, sua energia cinética é nula (Ec = mV2/2 = m.02/2=0).
Sendo os efeitos dissipativos desprezíveis você pode aplicar o Princípio da Conservação da energia Mecânica em que, para qualquer posição da trajetória, a energia mecânica (Em) é constante, ou seja, a soma das energias cinética (Ec) e potencial gravitacional (Ep) em cada ponto fornece sempre o mesmo valor.
Assim, se Em = Ec + Ep = constante, então no ponto x = x1 onde a cinética é nula a potencial será máxima.
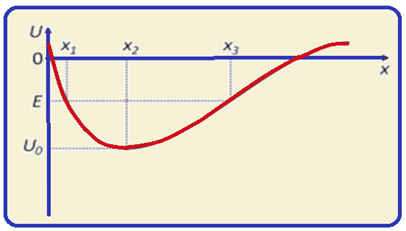
Da mesma maneira, se Em = Ec + Ep = constante, então no ponto x = x2onde a energia potencial gravitacional é mínima (veja gráfico) e de valor Uo, a cinética será máxima.
R- E
DINÂMICA IMPULSIVA
01–Cálculo das velocidades dos carrinhos 1 e 2 de massas m1 = 150 g e m2 pedida, antes do choque, registrados nos instantes O e 1 s fornecidos no quadro:
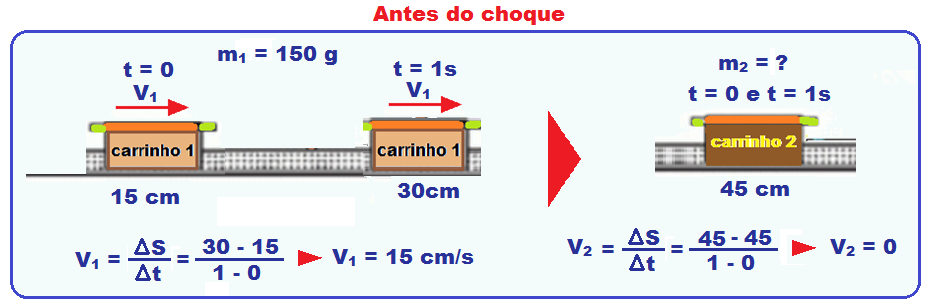
Após o choque, pelo enunciado eles se movem unidos (choque inelástico) com massa (M = 150 +m2), com a mesma velocidade V’ fornecida no quadro nos instantes 8s e 11 s:
Aplicando o teorema da conservação da quantidade de movimento:
Quantidade de movimento do sistema antes do choque Qsa = m1.V1 + m2.V2 = 150.15 + m2.0
Qsa = 2250 + 0 Qsa = 2250 g.cm/s.
Quantidade de movimento do sistema depois do choque Qsd = M.V’ = (150 + m2).5 = 750 + 5m2 Qsd = 750 + 5m2.
Qsa = Qsd 2250 = 750 + 5m2 m2 = 1500/5 m2 = 300 g.
R- C
02-As forças trocadas entre o trem e a camionete obedecem ao princípio da ação e reação, ou seja, tem sempre a mesma intensidade, mesma direção, mas sentidos contrários.
Choque inelástico
Neste tipo de choque a dissipação de energia é máxima, o coeficiente de restituição é nulo, e, após o choque, os corpos obrigatoriamente se juntam e se movem unidos com a mesma velocidade. Lembre-se de que em qualquer tipo de choque a quantidade de movimento sempre se conserva.
R- D
03-
04-Definimos impulso da força 
no intervalo de tempo ∆t como sendo a grandeza vetorial:
Como ∆t é uma grandeza escalar positiva, o impulso I tem sempre a mesma direção e mesmo sentido que a força e, com as características abaixo:
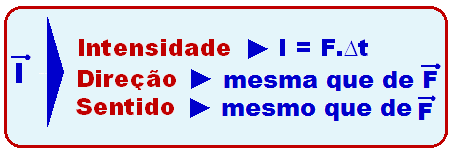
Observe no gráfico que, no intervalo de tempo entre 5 s e 105 s, a força de mantém constante em 100N, assim, em um intervalo de tempo de Δt =105 – 5 = 100 s, aplicando a fórmula do impulso, em modulo, temos I = F.Δt = 100.100 I = 10.000 N.s = 104 N.s.
OBS: repare que o exercício pede somente a intensidade do impulso, mesmo ela sendo uma grandeza VETORIAL (possui intensidade, direção e sentido).
05- I. Correta 
Quando temos uma colisão perfeitamente elástica significa que o sistema é conservativo, isto é, a quantidade de movimento e a energia cinética permanecem constantes.
IV. Errada Analogamente a afirmação III, como m1 < m2 
V’2 < V’1,porém, V’1 será menor que V1.
R- C
06- Sendo a colisão elástica a energia total (cinética do sistema constituído pelas 5 esferas) é a mesma antes e depois do choque e ocoeficiente de restituição vale e=1. Como em todo em tipo de choque, aquantidade de movimento do sistema também se conserva.
Se você chamar de m a massa de cada esfera e de V sua respectiva velocidade, o módulo da quantidade de movimento do sistema antes do choque (com as 3 esferas se movendo para a direita) é Qsa = mV + mV = mV = 3mV.
Assim, o módulo da quantidade de movimento do sistema depois do choque deve ser também Qsd =
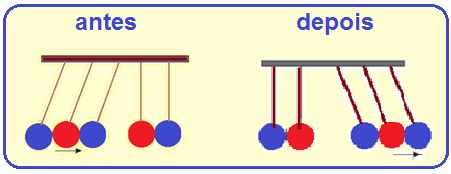
3mV é a única alternativa que satisfaz é a C.
R- C.
07-
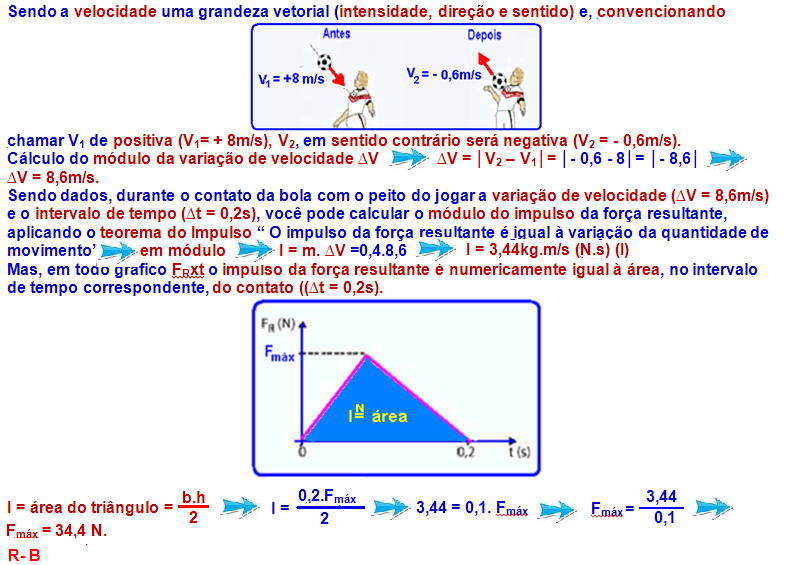
08-Supondo a cabeça do jogador parada (obstáculo fixo), o módulo quantidade de movimento da bola antes do choque, quando incide verticalmente com velocidade de módulo Vvertical será:
Qsa = mVvertical, com direção vertical e sentido para baixo.
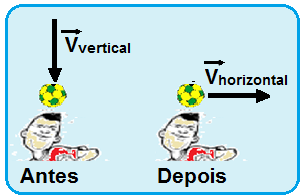
Supondo a cabeça do jogador parada (obstáculo fixo), o módulo da quantidade de movimento da bola depois do choque, quando retorna horizontalmente com velocidade de módulo Vhorizontal será:
Qsd = mVhorizontal, com direção horizontal e sentido para a direita.
09-
10-
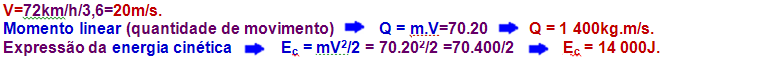
MOVIMENTO HARMÔNICO SIMPLES
01-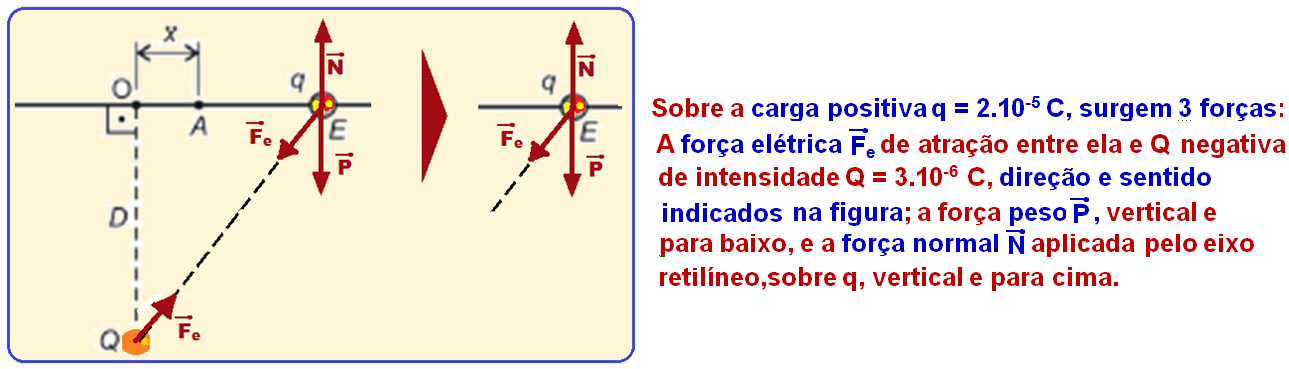
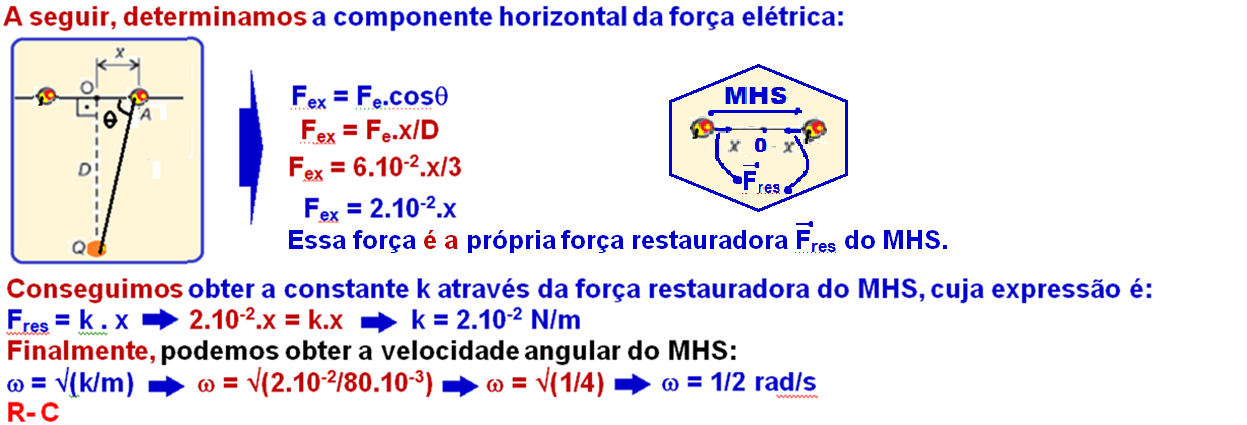
02-O período T (tempo que o oscilador massa-mola demora para efetuar uma oscilação “vai e vem” completa) é fornecido por:
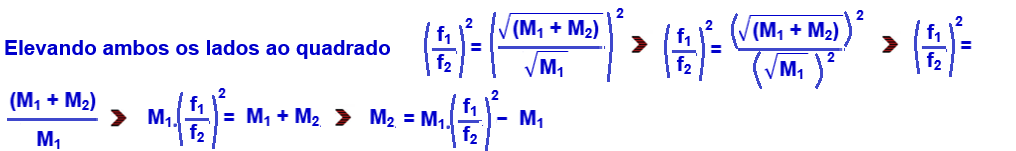
R- B
03-
01 Falso O período e a frequência dependem apenas do número de ciclos e do intervalo de tempo.
02 Verdadeiro A frequência no MHS pode ser calculada como:
Onde T é o período, m a massa desejada e k a constante elástica.Para calcularmos a frequência, precisamos elevar toda a equação por -1, pois a frequência é o inverso do período, nesse caso apenas vamos inverter as frações.
Colocando os valores:
Transformando 25.104 em 2500.102:
Saindo da raiz:
Simplificando:
