Resolução Comentada – Dinâmica Impulsiva – 2019/2018

Resolução Comentada – Dinâmica Impulsiva – 2019/2018

01-

Expressões matemáticas dos dois tipos de energias envolvidos no fenômeno

R- B

02-

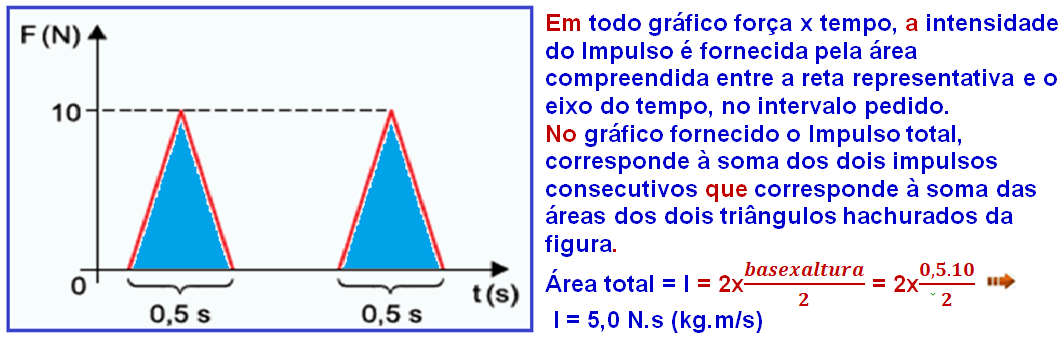
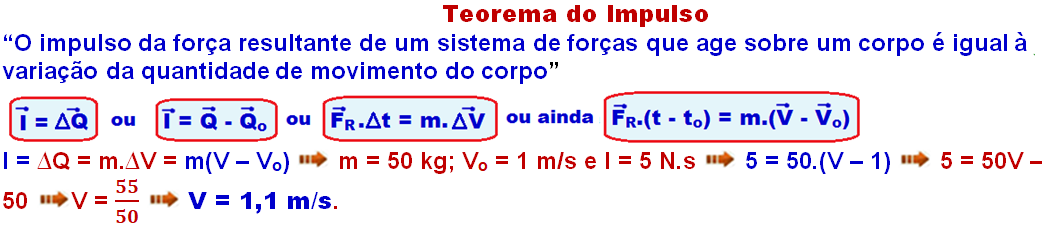
R- B

03-

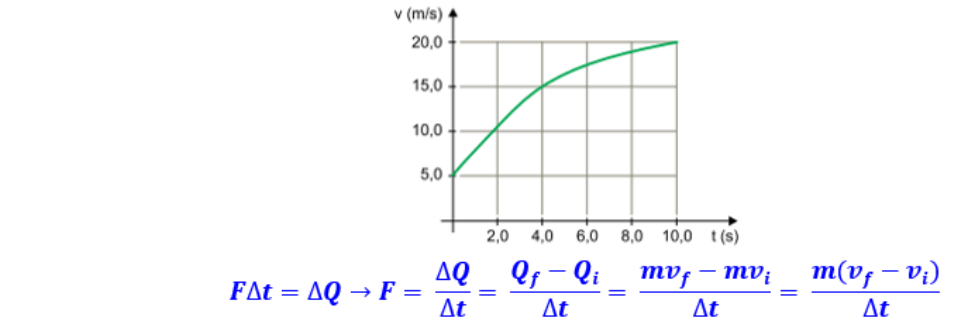
04-

A) Correta – A força resultante é a força centrípeta (Fc) de direção radial e sentido para o centro da

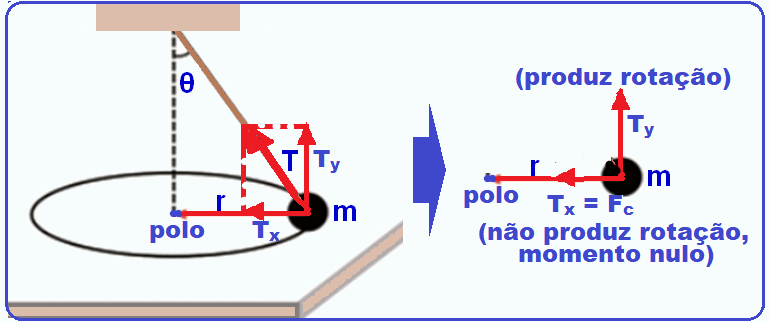
circunferência e, no caso, é apenas a parcela horizontal de T (Tx) que não produz rotação, que é produzida apena pela parcela vertical de T (Ty). Assim, o momento gerado pela força resultante (força centrípeta) é nulo.

B) Falsa – a quantidade de movimento possui módulo Q = m.V constante. Mas sua direção e sentido muda de acordo com a velocidade que é tangente à trajetória em cada ponto.

C) Falsa – veja (A)

D) Falsa – veja (A)

R- A

05-

Cálculo da intensidade da velocidade inicial Vo do sistema sabendo que ele está freando com aceleração a = – 5 m/s2 até parar V = 0 após se deslocar de ∆S = 10 m.

Equação de Torricelli  V2 = Vo2 + 2.a. ∆S  02 = Vo2 – 2.5.10 Vo2 = 100  Vo = 10 m/s (velocidade dos dois veículos juntos após o impacto).

Agora você deve aplicar o princípio da conservação da quantidade de movimento imediatamente antes e imediatamente após o impacto.

Antes  Qsa = mc.Vc + ms.Vs = 2000.Vc + 1000.0 = 2000Vc + 0  Qsa = 2000Vc.

Depois  Qsd = M.Vo = 3000.10  Qsd = 30000 kgm/s.

 R- E

06-

Considerando o sistema isolado de forças externas você pode utilizar o princípio da conservação da quantidade de movimento do sistema imediatamente antes e imediatamente depois da explosão.

Lembre-se que neste ponto (altura máxima) a velocidade VH é apenas a componente horizontal das velocidades vertical e horizontal do lançamento oblíquo. Assim ela tem módulo VH, direção horizontal e sentido para a direita.

Vamos supor que, após a explosão o fragmento A retorne com velocidade Va (veja figura).

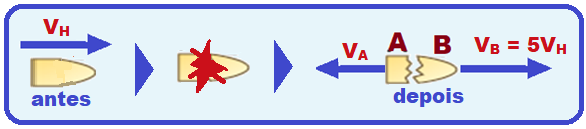
Quantidade de movimento do sistema antes da explosão  Qsa = (MA + MB).VH = (2MB + MB).VH  Qsa = 3MB.VH.

Quantidade de movimento do sistema depois da explosão  Qsd = MA.(-VA) + MB.(VB) = – 2MB.VA + MB.(5VH)  Qsd = – 2MB.VA + 5MB.VH.

Qsa = Qsd  3MB.VH = – 2MB.VA + 5MB.VH  3VH – 5VH = – 2VA  – 2VH = – 2VA  VA = VH.

Então o fragmento A retorna com velocidade VH possuindo trajetória invertida do lançamento oblíquo, percorrendo o mesmo caminho na volta e atingindo o ponto II.

R- E

07-

 

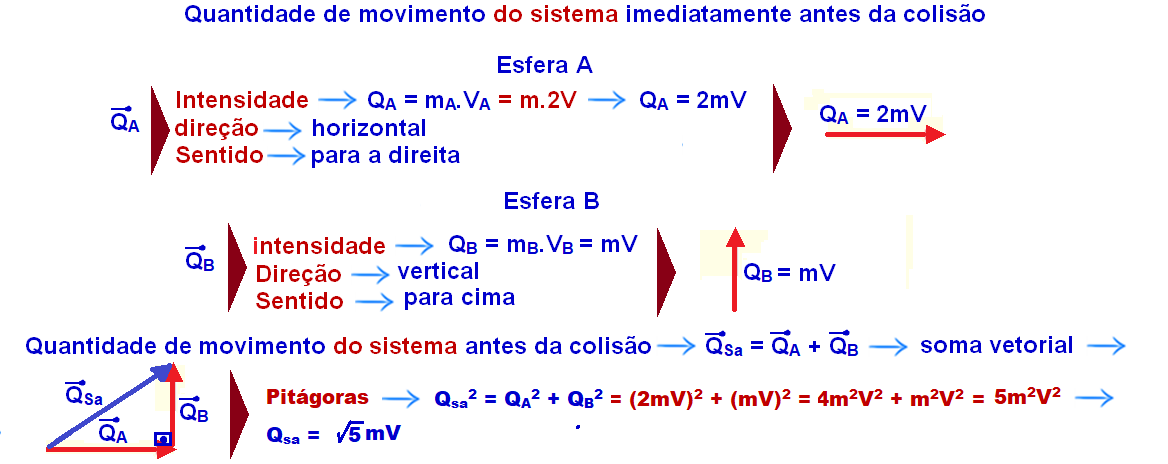
Pelo princípio da conservação da quantidade de movimento, em todo tipo de choques, a quantidade de movimento do sistema antes do choque Qsa é igual à quantidade de movimento do sistema depois do choque Qsd.

08-

Sempre que a colisão é perfeitamente elástica e os corpos possuem a mesma massa, eles trocam

suas velocidades, ou seja, se o bloco A atinge o B (VB = 0) com velocidade VA, imediatamente após a colisão, A para (VA) = 0 e B segue com velocidade VB = VA.

Desprezando os atritos e a resistência do ar o sistema pode ser considerado conservativo (energia

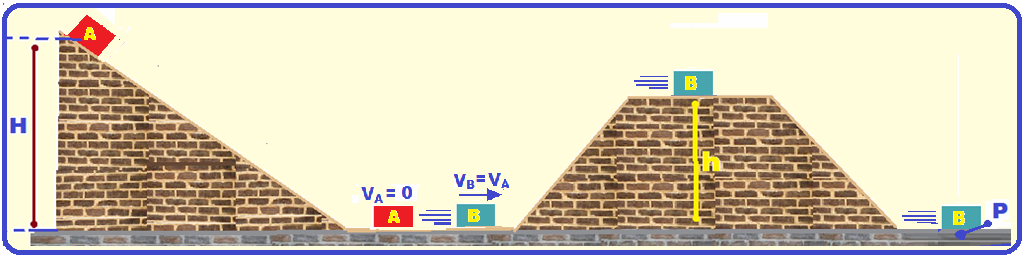
mecânica = energia cinética + energia potencial gravitacional) e assim o bloco B só pararia numa altura H. Como h < H, ele chega até o ponto P.

R- D

09-

Como elas ficam grudadas após a colisão o choque é inelástico e elas se movem, após o choque, unidas com a mesma velocidade v’ (veja figura abaixo).