Resoluções das questões de vestibulares por assunto de 2018/2019
Resoluções das questões de vestibulares por assunto de 2018/2019
01-
R- A
02-
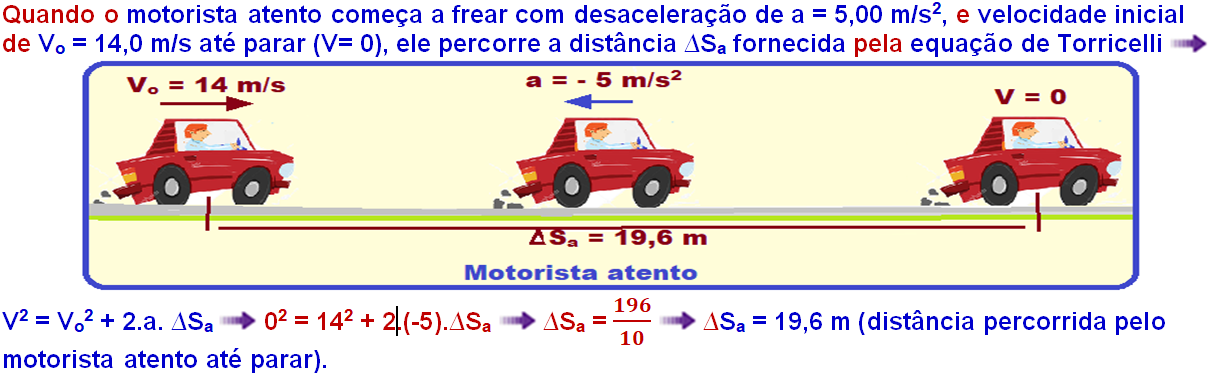
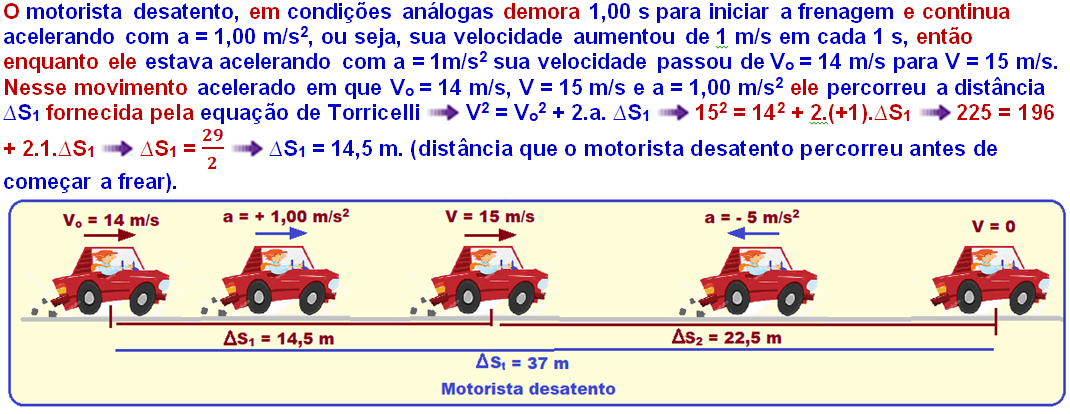
03-
04-
Se até o encontro A se moveu durante 40 s e B durante 50s, então B partiu 10 s depois de A.
R- B
Ou, simples raciocínio: Se, quando eles se encontram A se moveu durante 40 s, então com a mesma velocidade, B se moveu durante (90 – 40 = 50 s) o que significa que B partiu 10 segundos depois de A
05-
Basta prestar atenção no enunciado que afirma que o número de voltas efetuadas pela roda traseira a cada pedalada é calculado dividindo-se a quantidade de dentes da coroa pela quantidade de dentes da catraca e, fazendo isso você obtém a tabela abaixo:
Você deve escolher a menor razão que é aquela em que a roda traseira percorre a menor distância para fazer o percurso o mais devagar possível, fornecida pela alternativa IV.
R – D
06-
07-
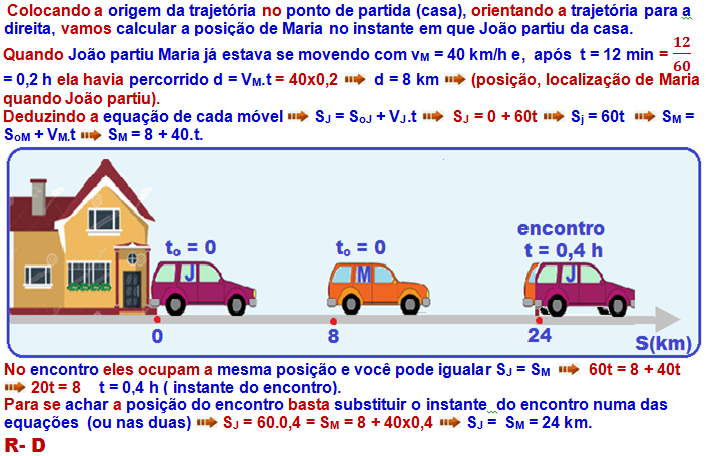
08-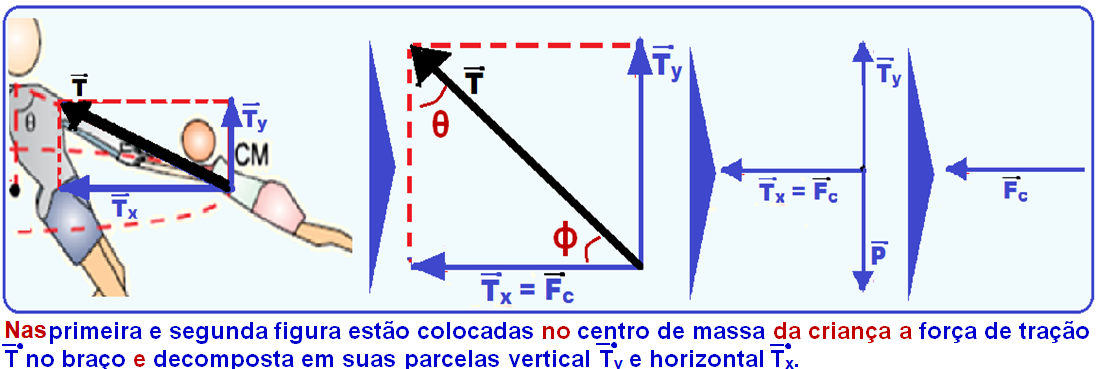
Veja as figuras abaixo:
R- A
09-
Veja abaixo, a figura ilustrativa da situação apresentada:
10-
11-
Bola 2
O mesmo é válido para a bola 2 só que agora Epa = 0,95%Epd 
m2gH = 0,95m2.gh2 h2 = 0,95H.
Como é pedida a diferença h2 – h1 você terá h2 – h1 = 0,95H – 0,75H = 0,20H
R- A
12-
Em m/s 
60/3,6 = 16,66 m/s 80/3,6 = 22,22 m/s veja na alternativa A que 15 m/sx3,6 = 54 km/h e que 25 m/sx3,6 = 90 km/h, ou seja, 60 km/h e 90 km/h estão compreendidos entre 54 km/h e 90 km/h.
R- A
13-
Resumo dos gráficos do espaço, velocidade e aceleração do MUV, com a > 0 e com
a < 0.
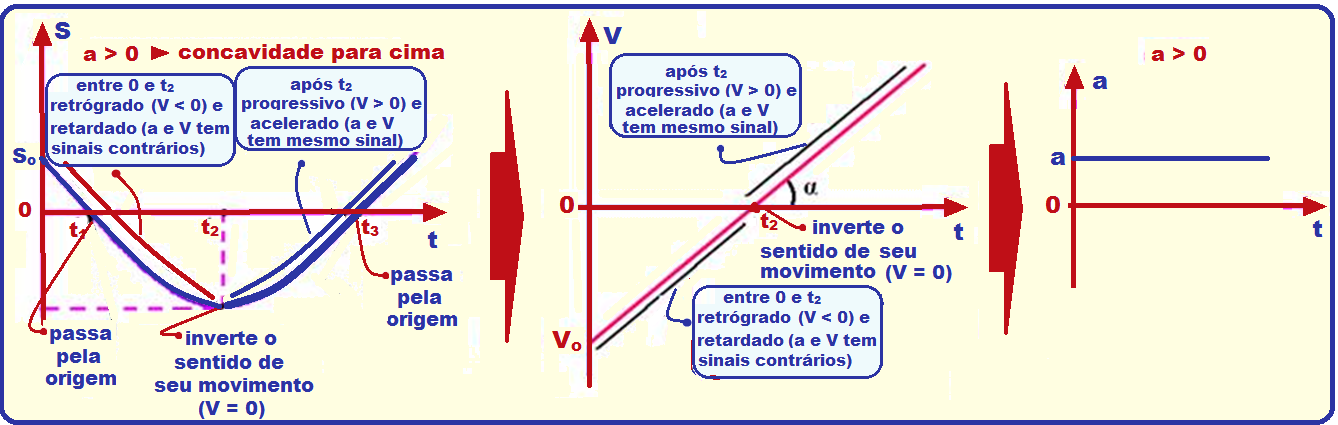
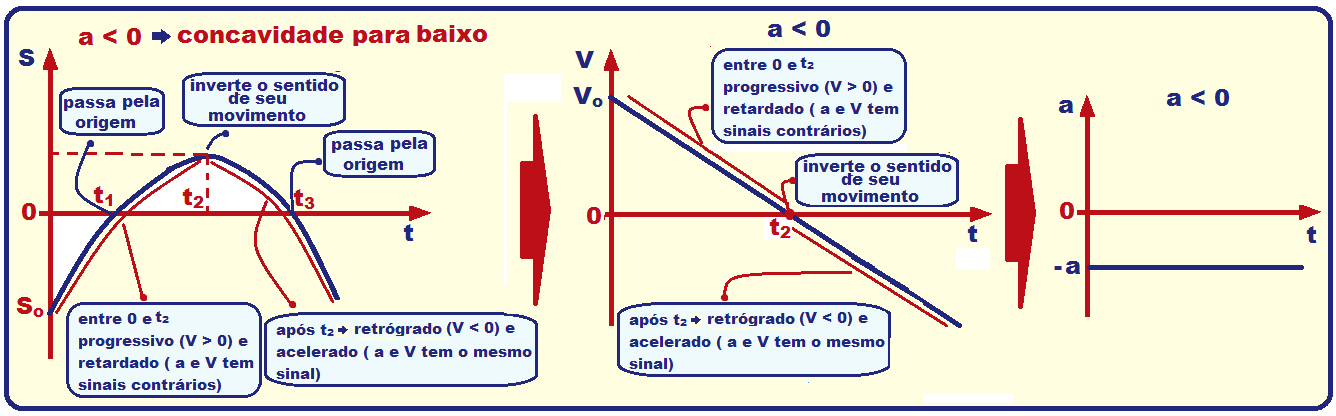R- D
14-
Colocando a origem das alturas no ponto Q e calculando a energia mecânica do corpo de massa m nos pontos P e Q:
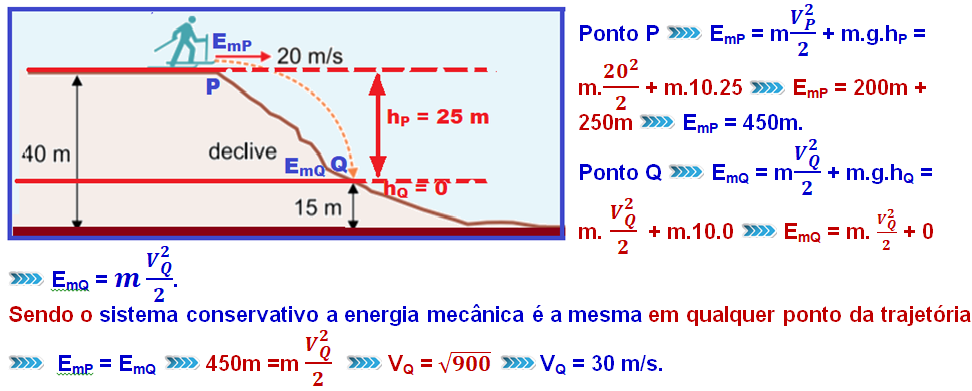
R- B
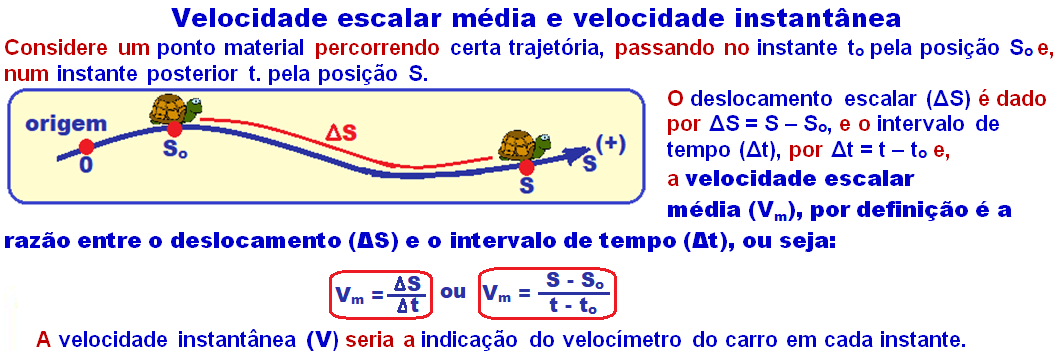
15-
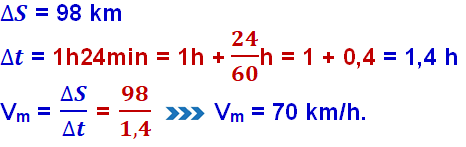
R- A
16-
Localizando os móveis no plano cartesiano:
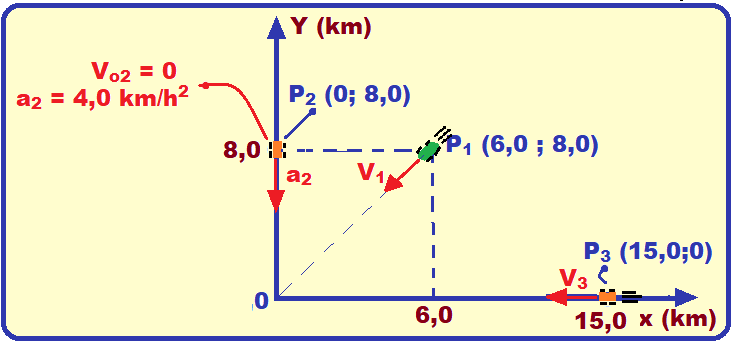
17-
No caso do exercício:
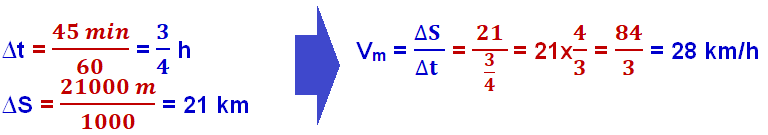
R- B
18-
Carro A 
VA = dA/tA V = L/tA tA = L/V.
Carro B VB = dB/tB 2V = 4L/tB tB = 4L/2V tB = 2(L/V) = 2 tA.
R- B
19-
20-
21-
R – B
22-
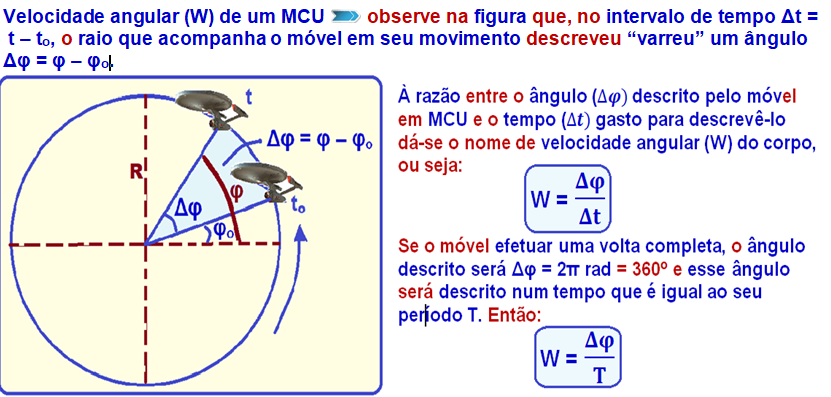
Os dois carros A e B da figura mantêm-se lado a lado numa pista circular, no mesmo intervalo de tempo Δt.
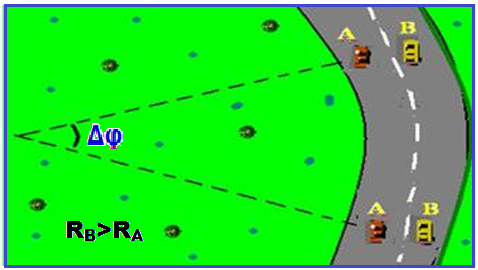
Seus raios nesse MCU são, respectivamente, RA e RB, com RB > RA.
O carro B terá maior velocidade (escalar, linear) V=ΔS/Δt, pois deverá percorrer maior distância ΔS para, no mesmo intervalo de tempo, poder acompanhar o carro A, ou seja, VA > VB. Mas, como “varrem” o mesmo ângulo (Δφ) no mesmo intervalo de tempo, suas velocidades angulares (W= Δφ/Δt) serão iguais, ou seja, WA = WB.
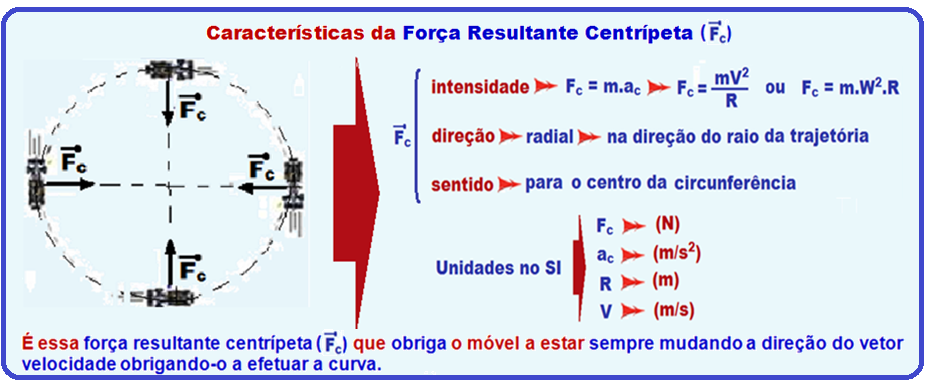
A velocidade angular W é a mesma para os dois carros (veja teoria acima) e como a intensidade da força centrípeta sobre cada um é fornecida por Fc = m.W2.R, essa expressão indica que Fc é diretamente proporcional ao raio R.
Então, se você dobrar R estará dobrando Fc (desde que as massas sejam as mesmas).
R – C
23-
São dados: Vo = 10 m/s; V = 20 m/s e t = 20 s.
Equação da velocidade do MUV V = Vo + a.t 20 = 10 + a.20 a = 10/20 a = 0,5 m/s2. (aceleração do movimento que é constante)
Equação horária do espaço do MUV ∆S = Vo.t + a.t2/2 = 10.20 + 0,5.202/2 = 200 + 0,5.200
∆S = 300 m
R – B
24-
Corpo abandonado de certa altura h do solo
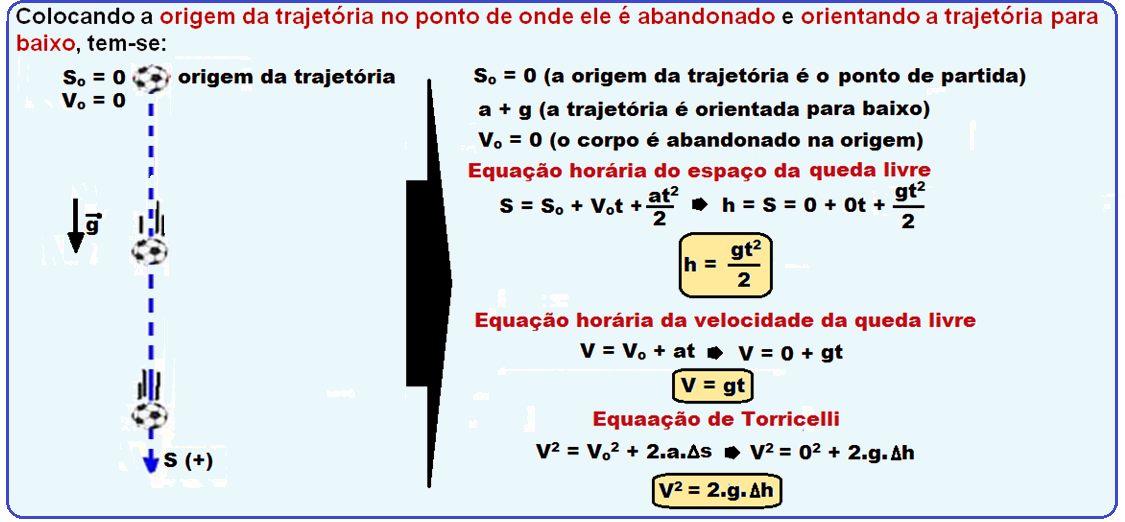
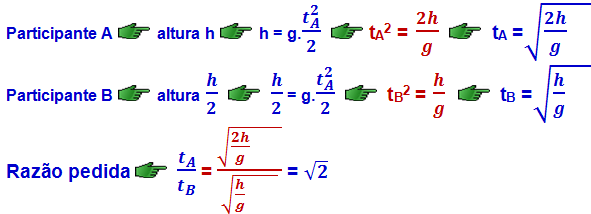
R- B
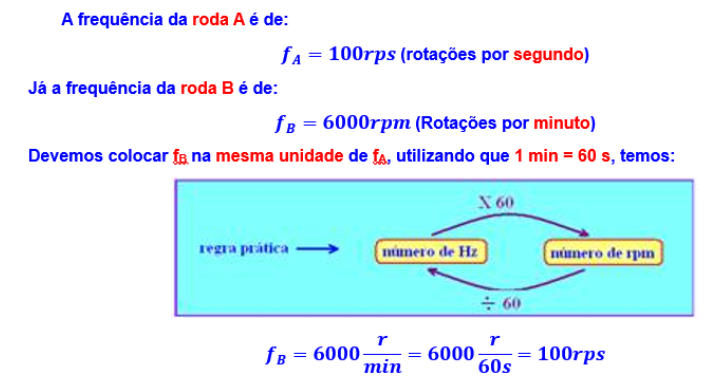
25-
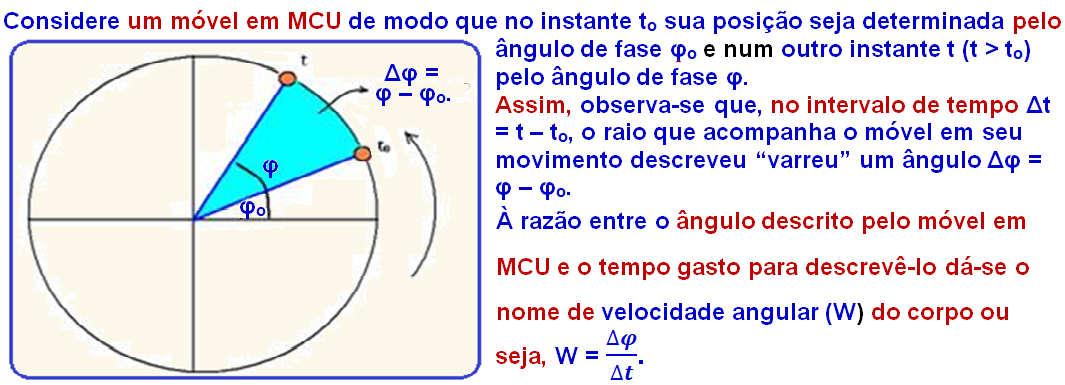
Velocidade angular (W) de um MCU
R- B
26-
R- D
27-
Veja o formulário abaixo
Corpo abandonado de certa altura h do solo
R- B
28-
R – A
29-
R- C
30-
A incorreta é a E, pois no instante t = 10s eles apresentam a mesma velocidade (V = 4 m/s) e não a mesma posição (localização).
R- E
31-
R- B
32-
R- C
33-
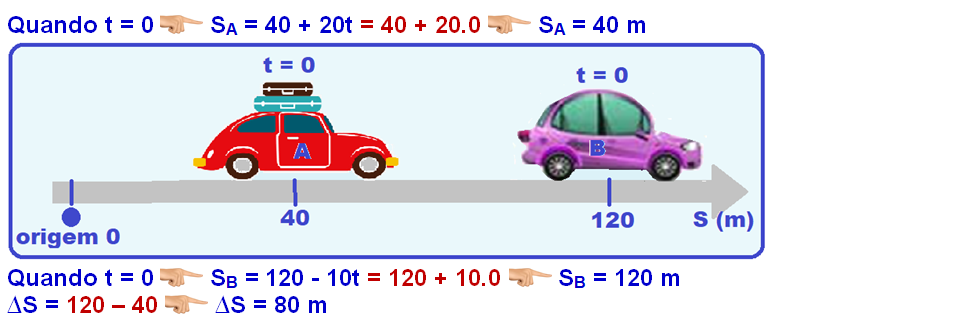
Observe nas equações (S = So + V.t) de cada movimento que VA = 40 m/s e VB = 50 m/s.
Colocando a origem em B (cB = 0), quando t = 0 você terá SA – SB = SoA – SoB = 50 SoA – 0 = 50 SoA = 50 m (quando B partiu de SoB = 0, A já estava na posiçao SoA = cA = 50 m.
Equação de A 
SA = 50 + VAt SA = 50 + 40t.
Equação de B SB = 0 + 50t SB = 50t.
No encontro SA = SB 50 + 40t = 50t 10t = 50 t = 5 s.
R- B
34-
A definição de repouso ou de movimento é a seguinte: “Um corpo está em repouso ou em movimento em relação a outro corpo quando a distância entre ele variar no decorrer do tempo. Caso contrário estará em repouso”.
A única afirmativa que satisfaz a definição acima é a D.
R- D
35-
Ultrapassagem
Trem (caminhão) de comprimento (x) atravessando um túnel (ponte) de comprimento ( c ) 
observe que para atravessar completamente o túnel (ponte), um ponto P fixo em qualquer parte do
trem (caminhão) deve percorrer uma distância ΔS = x + c, com velocidade V num intervalo de tempo Δt V = .
Ponte
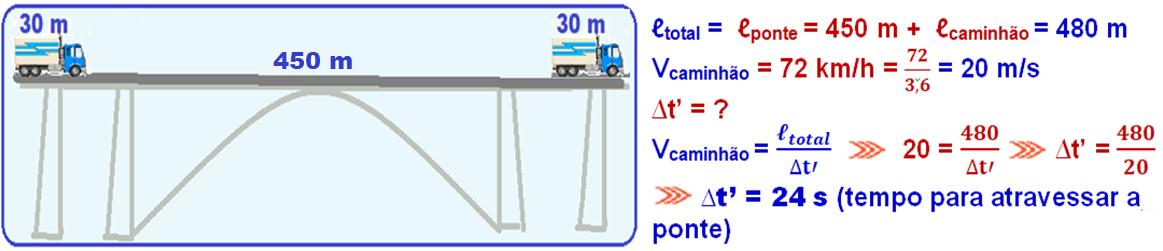
Túnel
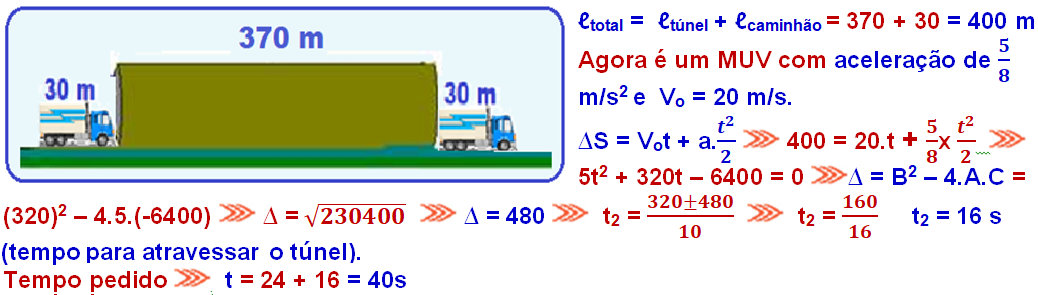
R- C
36-
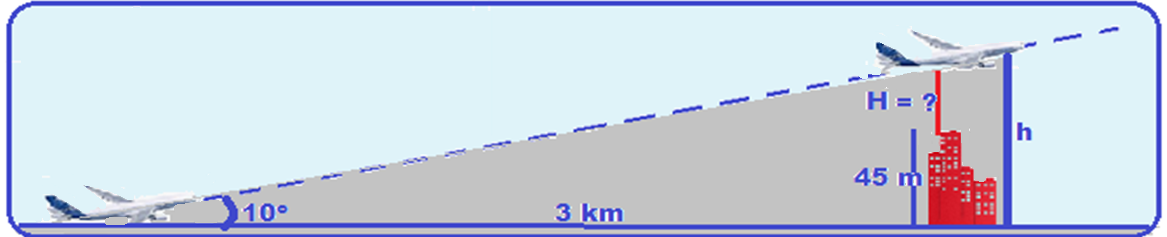
R- B
37-
Lançamento horizontal
Decompõe-se o movimento em duas parcelas: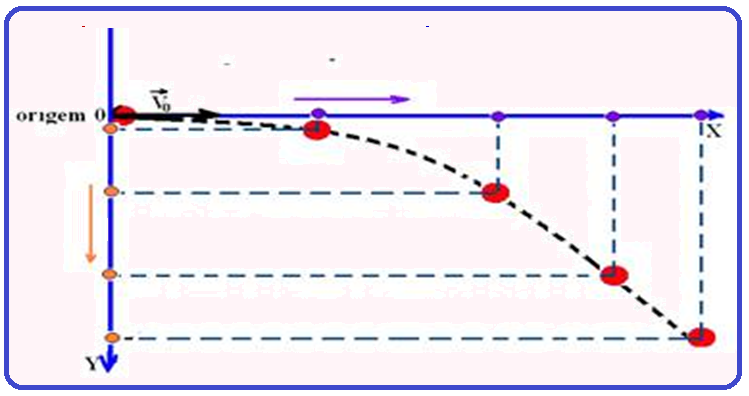
Segundo o eixo X 
trata-se de um movimento horizontal uniforme com velocidade constante de intensidade Vo, que é a velocidade de lançamento S = So + V.t X= 0 + Vo.t X =Vo.t
Segundo o eixo Y trata-se de um movimento uniformemente variado com velocidade inicial Vo = 0, ou seja, é uma queda livre com o corpo abandonado da origem, sujeito apenas à aceleração da gravidade, de intensidade g, direção vertical e sentido para baixo.
Equações:
S = So + Vo.t + at2/2 Y= 0 + 0.t + gt2/2 Y = g.t2/2
Vy = Voy + a.t Vy = 0 + g.t Vy = g.t
V2 = Vo2 + 2.a.ΔS Vy2 = Voy2 + 2.g.Δh Vy2 = 02 + 2.g.Δh Vy2 = 2.g.Δh
No caso do exercício:
R- E
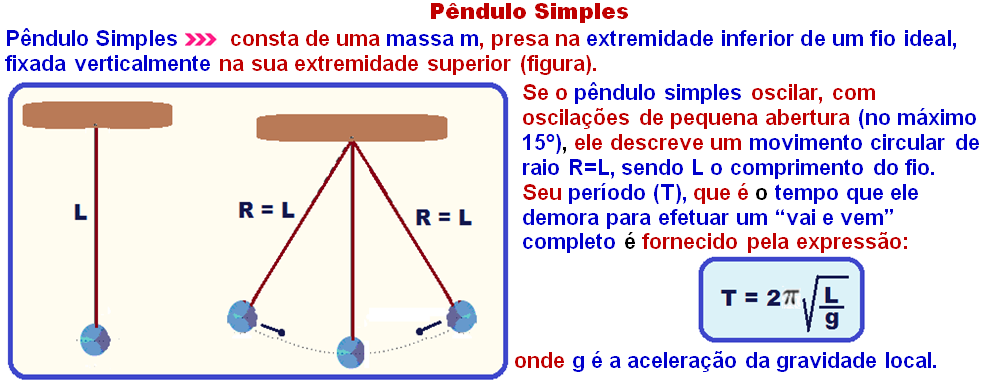
38-
Para cada volta completa da roda a distância percorrida DIST’ é fornecida pelo comprimento da circunferência da roda fornecida por DIST’ = 2πR (uma volta completa) onde R é o raio da roda. Se a roda efetua n voltas a distância percorrida será DIST = n.2πR.
R- D
39-
R- D
40-
