Resoluções Cinemática – 2013 – 2014
RESOLUÇÕES
MOVIMENTO UNIFORME
01- 01- I. Horário do rush — carro — Vmc=12km/h — ΔSc=12km — Vmc= ΔSc/Δtc — 12=12/Δtc — Δtc=1h — esse tempo é o mesmo que o do metrô fornecido pelo enunciado (1h) — Falsa
II. Horário do rush — carro — Vmc=12km/h — ΔSc=12km — Vmc= ΔSc/Δtc — 12=12/Δtc — Δtc=1h —
metrô — Vmm=60km/h — ΔSm=20km — Vmm= ΔSm/Δtm — 60=20/Δtm — Δtm=1/3h — Correta
III. Fora do horário de rush — carro — Vmc=42km/h — ΔSc=12km — 42=12/Δtc — Δtc=12/42=0,29h — metrô — Vmm=60km/h — ΔSm=20km — Vmm= ΔSm/Δtm — 60=20/Δtm — Δtm=1/3h=0,33h — Correta
IV. Fora do horário de rush — carro — Vmc=42km/h — ΔSc=12km — 42=12/Δtc — Δtc=12/42=0,29h — nova velocidade do metrô — Vmm=70km/h — ΔSm=20km — Vmm= ΔSm/Δtm — 70=20/Δtm — Δtm=2/7h=0,29h — Correta
R- E
02- 02- Distância total percorrida — ΔS=(1380 + 730 + 490 + 640 + 1080)=4320m — tempo total de viagem — Δt=(2,5 + 2,0 + 1,0 + 1,5 + 2,0)=9minx60=540s.
Vm= ΔS/Δt=4320/540=8m/s.
R- B
03-Tempo que o bondinho demora para percorrer o primeiro trecho AB da Praia Vermelha ao Morro da Urca
onde percorre ΔS1=540m com velocidade V1=10,8/3,6=3m/s — V1= ΔS1/Δt1 — 3=540/Δt1 — Δt1=540/3
Δt1=180s/60 — Δt1=3 min — o segundo BC trecho corresponde a uma caminhada no Morro da Urca
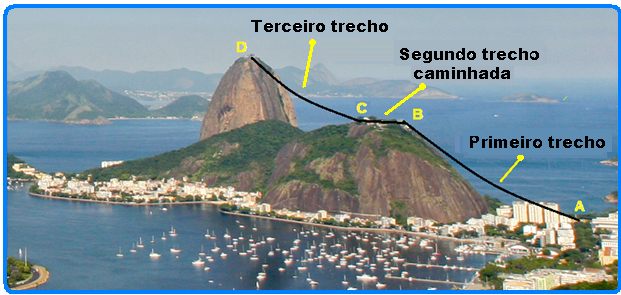
cujo tempo gasto somado ao tempo de espera nas estações é de Δt2=30 minutos (dado fornecido) —
no terceiro trecho CD, de bondinho, do Morro da Urca ao Pão de Açúcar ele percorreu ΔS3=720m com velocidade V3=14,4/3,6=4m/s e demorou Δt3 tal que — V3=ΔS3/ Δt3 — 4=720/Δt3 — Δt3=720/4=190s —
Δt3=3 min — tempo total do passeio — Δt=3 + 30 + 3=36 min. — R- D
04- Tempo que o corredor mais rápido (V1=32km/h) demora para completar os d1=100m=0,1km — V1=d1/t1 — 32=0,1/t1 — t1=0,1/32 h.
Nesse tempo t1=t=0,1/32 h o corredor menos rápido (V2=30km/h) percorreu a distância d2 tal que —
30=d2/(0,1/32) — d2=3/32=0,09375km=93,375m.
A distância pedida entre eles vale d’=100 – 93,375=6,25m
R- D
05- A) Sim, ambos no km 8, onde a reta representativa é paralela ao eixo dos tempos, mas em intervalos de tempos
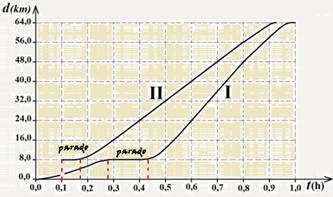
diferentes (veja gráfico acima)
B) (II) — Vm=(d – do)/(t – to)=(64 – 8))/(0,9 – 0)=56/0,9=62,2km/h — (I) — Vm=(d – do)/(t – to)=(64 – 0)/(0,95 – 0)=67,4km/h — a maior velocidade escalar média é a do veículo I.
C) Sim — os dois — o veículo I, por exemplo, entre 0,6h e 0,8h teve velocidade de VI=(48 – 24)/(0,8 – 0,6)=120km/h — o veículo II, por exemplo, entre 0,4h e 0,6h teve velocidade de VI=(48 – 24)/(0,6 – 0,4)=120km/h .
06- Cálculo da velocidade real de Carlos na hora correta — se o relógio adianta ∆ta=1min 40s=10 + 40s=100s, a hora real indicada será — ∆tC=1h – 100s=3600 – 100=3500s — ∆tC=3500s — velocidade correta de Carlos — VC=∆SC/∆tC — VC=3500m/3500s — VC=1m/s (velocidade correta de Carlos) — cálculo da velocidade real de Julieta na hora correta — se o relógio atrasa ∆ta=1min 40s=10 + 40s=100s, a hora real indicada será — ∆tC=1h + 100s=3600 + 100 =3700s — ∆tC=3700s — velocidade correta de Julieta — VJ=∆SJ/∆tJ — VJ=3500m/3700s — VC=0,9m/s — (velocidade correta de Julieta) — em ∆t=1h=3600s Carlos percorreu — VC=∆SC/∆tC — 1=∆SC/3600 — ∆SC=3600m — em ∆t=1h=3600s Julieta percorreu — VJ=∆SJ/∆tJ — 0,9=∆SJ/3600 — ∆SJ=3240m — ∆Spedido=∆SC – ∆SJ=3600 – 3240=360m — R- A.
07- Cálculo da distância d1 indicada na figura (triângulo hachurado) — tg30o=12/d1 — √3/3=d1/12 —

d1=4√3 — d1=4.1,7=6,8km=6800m — observe que você obtém um triângulo retângulo e que a distância AC=12km — assim, d2=12000 – 6800=5200m — V=1872km/h/3,6=520m/s — V=d2/t — 520=5200/t — t=10s — R-C.
08- Vm=∆S/∆t=(S – So)/(t – to)=(50 – 0)/(40 – 0) — Vm=1,25m/s — R- B.
09- – Primeiro trecho — Vm1=∆S1/∆t1 — 80=80/∆t1 — ∆t1=1h (intervalo de tempo que demora para

percorrer o primeiro trecho) — segundo trecho — Vm2=∆S2/∆t2 — 60=120/∆t2 — ∆t2=60/120 — ∆t2=0,5h ((intervalo de tempo que demora para percorrer o segundo trecho) — tempo necessário para efetuar a entrega — ∆t=∆t1 + ∆t2=1 + 0,5 — ∆t=1,5h — R- C.
10- Primeiro trecho: Trata-se de um movimento uniformemente acelerado, onde a locomotiva parte do repouso, com aceleração constante, sendo que esse movimento é expresso por uma função do segundo grau S=So + Vot + at2/2, onde o gráfico posiçãoxtempo é um arco de parábola com concavidade para cima (aceleração positiva).
Segundo trecho: Mantém velocidade constante e a função horária é do primeiro grau S=So + Vt, onde o gráfico posiçãoxtempo é uma reta inclinada ascendente.
Terceiro trecho: A composição freia até parar — trata-se de um movimento uniformemente retardado, com aceleração constante, sendo que esse movimento é expresso por uma função do segundo grau S=So + Vot + at2/2, onde o gráfico posiçãoxtempo é um arco de parábola com concavidade para baixo (aceleração negativa) — no trecho de parada enquanto a composição permanece em repouso, o gráfico é uma reta paralela ao eixo dos tempos.
R- C.
11- Correndo sem vento, o velocista demora ∆t=10s para percorrer ∆S=100m — correndo com o vento a favor, para percorrer os mesmos ∆S=100m ele demora ∆t’=10,0 – 0,1=9,9s — com vento a favor — V=∆S/∆t’=100/9,9 —
V=10,101m/s — R- C.
Movimento Uniformemente variado (MUV)
01- Cálculo da aceleração a — a=∆V/∆t=(28 – 4)/(7 – 1)=24/6 — a=4m/s2 — quando t=7s, V=28m/s — V=V0 + at — 28= Vo + 4.7 — Vo=1m/s — o deslocamento ∆S entre 3s e 5s é fornecido pela área do trapézio — ∆S=área=(B +
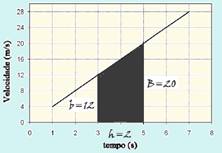
b).h/2 — ∆S=(20 + 12).2/2 — ∆S=32m — R- C.
02- Vo=30m/s — V=? — a=-5m/s2 (freando) — ΔS=50m — equação de Torricelli — V2=Vo2 + 2.a.ΔS — V2=302 + 2.(-5).50=900 – 500 — V=√400 — V=20m/sx3.6=72km/h — R- E
03- 

R- E
04-

R- B
05- Em todo gráfico Vxt, o deslocamento é numericamente igual à área entre a reta representativa e o eixo t — se o motorista não tivesse reduzido a velocidade do veículo e mantido a velocidade constante de
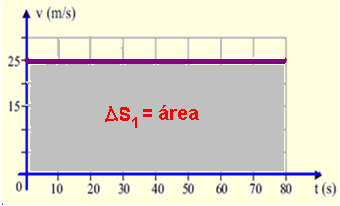
V=90km/h=25m/s, a distância percorrida seria a área ΔS1 da figura abaixo — ΔS1=b.h=80×25=2000m — ΔS1=2000m
A distância (ΔS2) que ele realmente percorreu devido às obras corresponde à soma das áreas da figura abaixo — A1=b.h=10×25=250m — A2=(B + b).h/2=(25 + 15).10/2=200m — A3=b.h=20×15=300m —

A4=(B + b).h/2=(25 + 15).20/2=400m — A5=b.h=20×25=500m — ΔS2=250 + 200 + 300 + 400 + 500= 1650m — ΔS2=1650m — se ele não tivesse reduzido a velocidade devido às obras a distância adicional percorrida seria de d=2000 – 1650=350m —d=350m — R- D
Observação: Você poderia também subtrair as áreas, conforme as figuras abaixo e, nesse caso, a distância

d pedida seria a área do trapézio — d=(B +b).h/2=(50 + 20).10/2=350m — d=350m
06- Se você fixar um ponto P no início da locomotiva , quando P começar a passar diante do observador (marco inicial 0), você terá velocidade inicial Vo e to=0, e quando a locomotiva terminar de passar pelo observador P estará a 24m de 0 no instante t=4s (figura I).
Pelo enunciado, quando o primeiro vagão terminar de passar pelo observador o ponto P estará a 48m de 0 e o instante será t=4 + 2 = 6s (figura II)
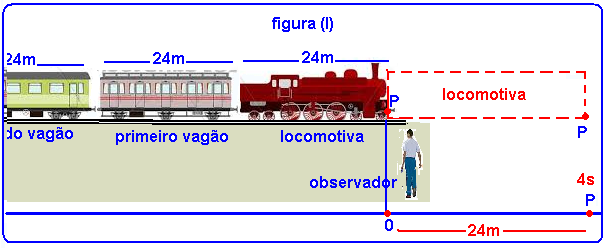

Na figura I, quando t=4s o ponto P, com velocidade inicial Vo e aceleração a, percorreu ΔS=24m —
ΔS= Vot + at2/2 — 24 = vo.4 + a.42/2 — 24 = 4Vo + 8a — 6 = Vo + 2a — Vo= 6 – 2a (1).
Na figura II, quando t=6s o ponto P, com velocidade inicial Vo e aceleração a, percorreu ΔS=48m —
ΔS= Vot + at2/2 — 48 = Vo.6 + a.62/2 — 48 = 6Vo + 18a — 8 = Vo + 3a (2).
(1) em (2) — 8=6 – 2a + 3a — a=2m/s2 (aceleração da composição).
Vo= 6 – 2.2 — Vo=2m/s (velocidade inicial do ponto P).
Quando o primeiro vagão começa a passar diante do observador o ponto P está na posição 24m e o instante é t=4s — V=Vo + at=2 + 2.4=10m/sx3,6=36km/h.
R- D
07- Colocando a origem da trajetória no ponto de partida do carro1 e orientando-a para a direita, quando 1 parte do
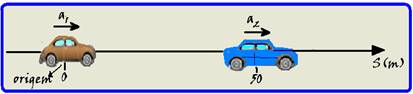
repouso do marco zero, 2 parte também do repouso do marco 50m — equação horária do carro 1 — S1=So1 + Vo1t + a1t2/2=
0 + 0 + a1t2/2 — S1=0,5.a1.t2 — S2=So2 + Vo2t + 2a1t2/2=50 + 0 + a1t2 — S2=50+ a1t2 — no encontro S1 = S2 —
0,5.a1.t2= 50 +a1.t2 — 0,5a1t2=50 — a1t2=100 — substituindo a1t2=100 em S1 — S1=0,5.100=50m — substituindo a1t2=100 em S2 — S2=50 + 100=150m — assim, o carro 2 alcança o carro 1 após percorrer ∆S=150 – 50=100m — R- C.
08- Como, durante a frenagem eles percorrem a mesma distância, a distância mínima, d, entre eles para que não ocorra colisão deve ser a distância percorrida pelo carro II durante o tempo de reação (t=0,6s) com velocidade de V=20m/s — V=d/t — 20=d/0,6 — d=12m — R- D
09- Colocando a origem da trajetória orientada para a direita no ponto onde a viatura parte com Vo=0 e localizando o carro nesse instante, ele estará no marco S-Vc.t=20.5=100m, você terá a situação esquematizada na figura abaixo —
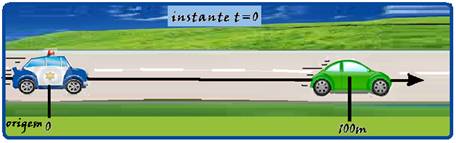
Equação da viatura — Sv=So + Vot + at2/2 — Sv=0 + 0.t + at2/2 — Sv=at2/2 (I) — equação do carro — Sc=So + Vct — Sc=100 + 20t (II) — no encontro, pelo enunciado, o carro está no marco Sc=2100m, que substituído em (II) fornece o instante do encontro — 2100=100 + 20t — t=2000/20=100s — a viatura nesse instante t=100s também está no marco Sv=2100m, que substituído em (I) fornece sua aceleração — 2100=a.1002/2 — a=2100/5000 — a=0,42m/s2 — velocidade da viatura no encontro quando t=100s — V=Vo + at=0 + 0,42.100=42m/s — R- E.
10- Em todo gráfico VXt a área entre a reta representativa e o eixo dos tempos é numericamente igual à variação de espaço ΔS, entre dois instantes quaisquer t1 e t2, no caso entre 0 e 15s — cálculo do deslocamento do carro A pela

áreahachurada do trapézio da figura — ∆SA=(B + b)xh/2=(15 + 10)x10/2 — ∆SA=25×5=125m (deslocamento do carro A em 15s – ∆SA=125m) — cálculo do deslocamento ∆SA do carro A entre 0 e t (veja figura abaixo) — ∆SA=(B + b).h/2=[t + (t – 5].10/2 — ∆SA=(2t – 5).5 — ∆SA=10t – 25 — equação do carro A — SA= SoA + ∆SA = 0 + 10t – 25 — SA=10t – 25 (I) — cálculo do deslocamento ∆SB do carro B entre 0 e t (veja figura abaixo) —

∆SB=(B + b).h/2=[t + (t – 8].(-10)/2 — ∆SB=(2t – 8).(-5) — ∆SB=-10t + 40 — equação do carro B — SA= SoB + ∆SB = 3 – 10t + 40 — SB=-10t + 43 (II) — nesse instante t, a distância entre os carros A e B é fornecida e vale dAB=332m — dAB=SA – SB — 332=10t – 25 – (- 10t + 43) — 332=20t – 68 — t=400/20 — t=20s.
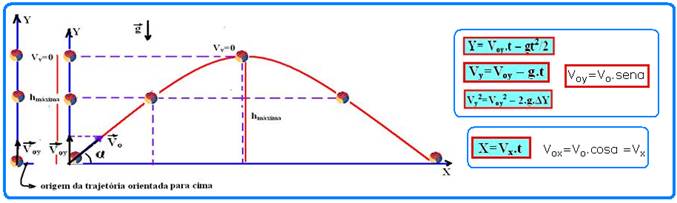
Lançamento obliquo
01-
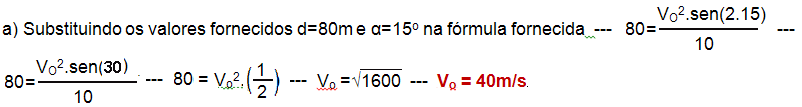
b) Pelo enunciado, o melhor ângulo possível ocorre quando o alcance é máximo e, o maior valor para sen (2α) ocorre quando α=45o, pois sen(2α)=sen(2.45o)=sen90o=1 — 98=Vo2.1 10 — Vo=√980≈31msx3,6 —
Vo ≈ 111km/h
02- Cálculo da intensidade velocidade inicial da bola na vertical Voy=V0.sen45o, Voy=(√2/2).Vo e na
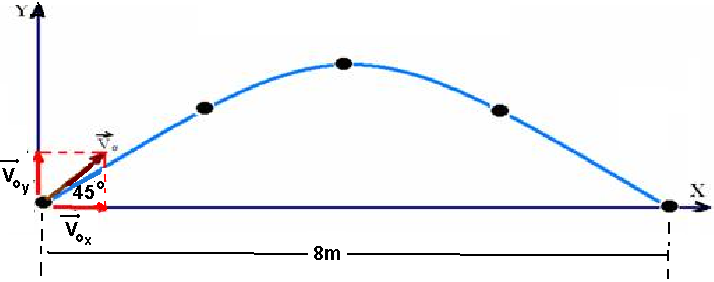
horizontal, Vox=(√2/2).Vo


R- D
03- Trata-se de um lançamento obliquo com ângulo de 45o com a horizontal e velocidade de V=20m/s.
Tempo que a bola demora para subir e descer na vertical com Voy=20.√2/2=10√2m/s e quando chega novamente ao solo Vy= – 10√2m/s — -10√2 = 10√2 – gt — -20√2 = -10t — t=2√2s
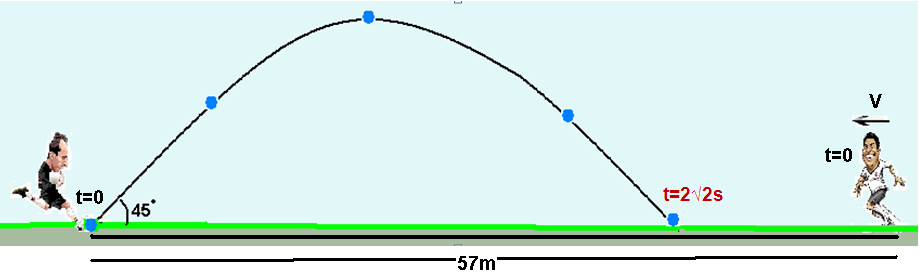
Esse tempo t=2√2s é o mesmo tempo que a bola demora para percorrer a distância horizontal x com velocidade constante Vox=Vocos45o=20. √2=10√2m/s — Vox=x/t — 10√2=x/2√2 — x=40m.
Nesse mesmo tempo t=2√2s o jogador deve percorrer d=57 – 40=17m com velocidade V tal que —V=d/t=17/2√2=17/2.1,4=17/2,8 — V=6,07m.
R- C
04- O observador A, dentro do vagão observa a trajetória da pedra como um laçamento vertical para
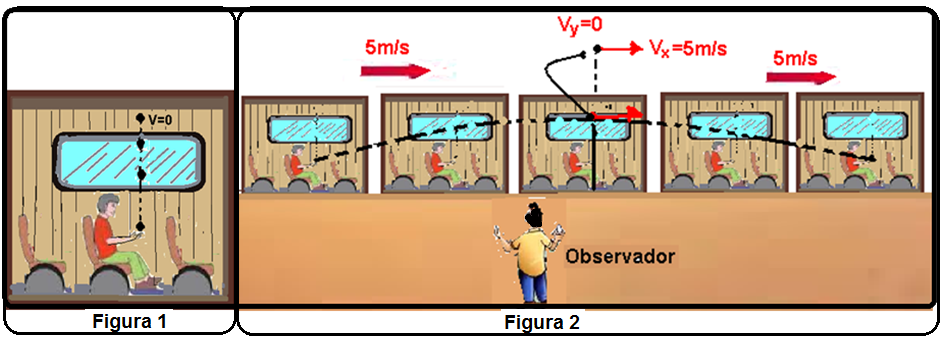
cima e, no ponto mais alto da trajetória a velocidade da pedra é zero, pois, nesse instante ela para e em seguida começa a retornar (figura1).
O observador B do lado de fora do vagão e em repouso em relação à Terra, observa o vagão passar e vê a trajetória da bola como um arco de parábola (lançamento oblíquo) e, no ponto mais alto da trajetória a velocidade vertical é nula mas a horizontal é constante e vale V=5m/s (figura 2).
R- B
05- Cálculo de Voy quando a bola atinge a altura máxima hmax=10m, onde Vy=0 utilizando a equação de Torricelli — Vy2 = Voy2 – 2.g.hmáx — 02 = Voy2 – 2.10.10 — Voy = √(200) m/s.
Cálculo de Vox com Vo fornecida e igual a 20m/s — Vo2 = Vox2 + Voy2 — 202 = Vox2 + {√(200)}2 —
Vox=√(200) m/s.
Na horizontal o movimento é uniforme com Vox=√(200)m/s (constante) e a bola demora 2s para atingir a parede —x=Voxt=√(200).t=14.2 — x≈28m.
R- B
06- Segundo a vertical, a componente da velocidade inicial vale Voy=Vo.sen30o=20.1/2 — Voy=10m/s e a aceleração é a da gravidade g=10m/s2 — estudando o movimento na vertical você verifica que trata-se de um lançamento vertical para cima — colocando a origem no ponto de lançamento, orientando a trajetória para cima e aplicando a equação de
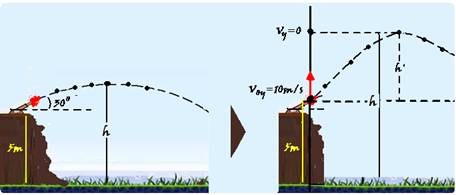
Torricelli lembrando que na altura máxima h’ a velocidade vertical é nula, Vy=0 — Vy2 = Voy2 – 2.g.h’ — 02 = 102 –
2.10.h’ — h’=100/20=5m — como a altura pedida é em relação ao solo — h=5 + 5=10m — R- B.
07- a) Em todo lançamento oblíquo o movimento na direção horizontal é retilíneo e uniforme, com velocidade horizontal , valendo — Vx=Vox=Vocos45o — Vox=Vo.√2/2 — Vox=1,4Vo/2 — Vox=(√2/2)Vo — equação do movimento na horizontal — x=xo + Voxt — para percorrer os x=80m na horizontal ele demora certo tempo t — 80=0 + (√2/2)Vot — t= 80√2/Vo (I) — na direção vertical quando a bola chega ao solo, no instante t, ela ocupa a
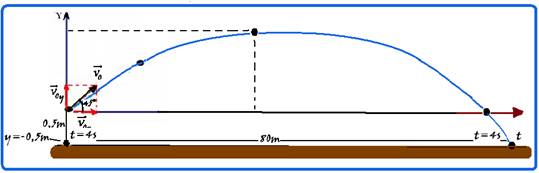
ordenada y=-0,5m sendo lançada com velocidade inicial vertical Voy=Vosen45o — Voy=(√2/2).Vo — equação de um lançamento vertical — y=yo + Voyt – gt2/2 — – 0,5 = 0 + (√2/2).Vo.80√2/Vo – 5.t2 — -0,5 = 80 – 5t2 — t2=80,5/5=16,1 — t≈4s (tempo que demora para percorrer 8om na horizontal, que é o mesmo tempo que demora para subir, descer e chegar ao solo) — substituindo t=4s em (I) — t= 80√2/Vo — 4= 80√2/Vo — Vo = 80√2/4=28m/s — Vo=28m/s ou Vo=20√2m/s.
b) Na altura máxima a componente vertical da velocidade é nula (Vy=0) — equação de Torricelli — Vy2 = Voy2 – 2.g.hmax — 02 = [Vo. (√2/2)]2 – 2.10.hmax — 02 = [20√2.(√2/2)]2 – 2.10.hmax — 02=400 – 20hmax — hmax=20m (em relação ao ponto de lançamento) — em relação ao solo a altura máxima atingida será — Hmax=20,0 + 0,5 — Hmax=20,5m.
08- Trata-se de um lançamento oblíquo e, se você não domina a teoria você a encontrará em fisicaevestibular.com.br – mecânica – cinemática – lançamento obliquo — em todo lançamento oblíquo, no ponto mais alto da trajetória a

componente vertical da velocidade (![]() ) é nula existindo apenas a componente horizontal (
) é nula existindo apenas a componente horizontal (![]() ) que é constante e de intensidade — Vx=Vox=Vo.cos60o=30.0,5=15m/s — R- B.
) que é constante e de intensidade — Vx=Vox=Vo.cos60o=30.0,5=15m/s — R- B.
09- Trata-se de um lançamento horizontal cuja teoria é fornecida a seguir:
Colocando-se a origem do sistema de referência no ponto de lançamento, orienta-se, por exemplo, o eixo X para a direita e o eixo Y para baixo.
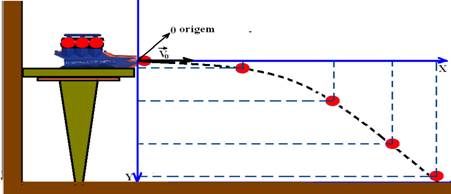
Decompõe-se o movimento em duas parcelas:
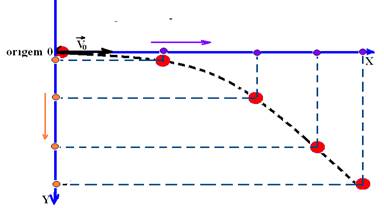
![]() Segundo o eixo X — trata-se de um movimento horizontal uniforme com velocidade constante de intensidade Vo, que é a velocidade de lançamento — S = So + V.t — X= 0 + Vo.t — X=Vo.t
Segundo o eixo X — trata-se de um movimento horizontal uniforme com velocidade constante de intensidade Vo, que é a velocidade de lançamento — S = So + V.t — X= 0 + Vo.t — X=Vo.t
![]() Segundo o eixo Y — trata-se de um movimento uniformemente variado com velocidade inicial Vo=0, ou seja, é uma queda livre com o corpo abandonado da origem, sujeito apenas à aceleração da gravidade, de intensidade g, direção vertical e sentido para baixo. Equações:
Segundo o eixo Y — trata-se de um movimento uniformemente variado com velocidade inicial Vo=0, ou seja, é uma queda livre com o corpo abandonado da origem, sujeito apenas à aceleração da gravidade, de intensidade g, direção vertical e sentido para baixo. Equações:
S = So= + Vo.t + at2/2 — Y= 0 + 0.t + gt2/2 — Y=g.t2/2
Vy = Voy + a.t — Vy= 0 + g.t — Vy=g.t
V2=Vo2 + 2.a.ΔS — Vy2 = Voy2 + 2.g.Δh — Vy2 = 02 + 2.g.Δh — Vy2 = 2.g.Δh
O tempo de movimento na horizontal é o mesmo de queda e vale t=0,6s — na horizontal, Segundo o eixo X — X=Vot=8.0,6=4,8m — na vertical, segundo o eixo Y — Y=g.t2/2=10.(0,6)2 — Y=1,6m — no instante em que as pedras chegam ao vagão elas possuem duas velocidades, a horizontal de valor Vx=8m/e e a vertical de valor — Vy=gt =10.0,6=6m/s — a velocidade com que as pedras chegam ao vagão corresponde à soma vetorial das velocidades Vx e
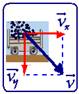
Vy — V2=Vx2 + Vy2=82 + 62 — V=10m/s — R- D.
10- Abaixo estão as equações de um lançamento oblíquo:
A. Falsa — Vox=Vx=Vo.cos θ=100.0,8=80m/s.
B. Falsa — Voy=Vo.senθ=100.0,6=60m/s.
C. Falsa — tempo para atingir a altura máxima — Vy=Voy – gt — 0=60 – 10t — t=6s — tempo de permanência no ar — t=2.6=12s — alcance horizontal — x=Voxt=80.12=960m.
D. Falsa — na altura máxima t=6s — y=Voyt – gt2/2 = 60.6 – 10.62/2=240m.
E Correta — Veja (C).
R- E.
MOVIMENTO CIRCULAR
01- Velocidade escalar (V) de um MCU ![]() Para qualquer móvel em MCU, que percorre espaços iguais em intervalos de tempo iguais), o espaço percorrido (ΔS) durante um período (Δt=T que é o intervalo de tempo que ele demora para efetuar uma volta completa) será ΔS=2
Para qualquer móvel em MCU, que percorre espaços iguais em intervalos de tempo iguais), o espaço percorrido (ΔS) durante um período (Δt=T que é o intervalo de tempo que ele demora para efetuar uma volta completa) será ΔS=2![]() , onde R é o raio da circunferência.
, onde R é o raio da circunferência.
ΔS=2![]() R e Δt=T — V= ΔS/Δt — V=2
R e Δt=T — V= ΔS/Δt — V=2![]() R/T
R/T

Lembrando que a frequência f de um MCU corresponde ao numero de voltas completas que o móvel efetua na unidade de tempo e que a frequência é o inverso do período, que f=1/T e que T=1/f você terá
V=2![]() R/(1/f) — V=2
R/(1/f) — V=2![]() Rf — o exercício fornece — R=60cm=0,6m — f=300rpm=300/60 rps — f=5 Hz —
Rf — o exercício fornece — R=60cm=0,6m — f=300rpm=300/60 rps — f=5 Hz — ![]() — V=2
— V=2![]() Rf=2x3x0,6×5 — V=18m/s —– R- B
Rf=2x3x0,6×5 — V=18m/s —– R- B
02- Se você não domina a teoria, ela está a seguir:
Acoplamento de polias e engrenagens
![]() Pode-se interligar duas ou mais polias através de uma correia (figura 1) ou acoplar duas ou mais engrenagens (figura 2)
Pode-se interligar duas ou mais polias através de uma correia (figura 1) ou acoplar duas ou mais engrenagens (figura 2)
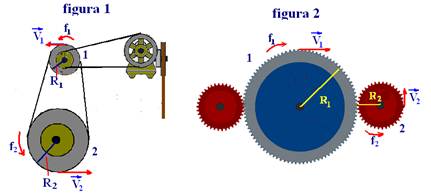
Todos os pontos da correia (admitidos inextensíveis) têm a mesma velocidade escalar V que todos os pontos da periferia de cada polia, desde que não ocorra deslizamento.
O mesmo ocorre com todos os dentes da polia engrenada, que tem a mesma velocidade escalar V.
Assim, V1=V2 — W1.R1 = W2.R2 — 2π/T1.R1= 2π/T2.R2 — 2πf1.R1 = 2πf2.R2
![]()
Veja na figura abaixo que que, se o raio da engrenagem A é RA, o da B será RB=(11 – RA)
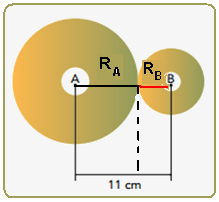
fA=375 voltas — fB=1000 voltas
fA.RA=fB.RB — 375.RA = 1000.(11 – RA) — 375RA=11000 – 1000RA — 1375RA=11000 — RA=
11000/1375 — RA=8cm — é pedido o raio da menor que é a B — RB=11 – 8 — RB=3cm
R- B
03- 01. Correta — pelo enunciado, o número de voltas da catraca é proporcional ao número de voltas da coroa, com razão de proporção igual à razão entre os raios da coroa (R) e da catraca (r) — fcatraca/fcoroa = R/r — pelo enunciado fcoroa=1 —fcatraca/1 = R/r — fcatraca=R/r.
02. Correta — fcatraca/fcoroa = R/r — observe em R/r que, como r é constante, se você diminuir R , o quociente R/r=k irá diminuir — então fcatraca/fcoroa=R/r — fcatraca =/fcoroa.R/r observe que r é inversamente proporcional à fcatraca — se r diminui, fcatraca aumenta fazendo com que a roda gire mais, percorrendo uma distância maior.
O4. Falsa — a de menor raio “varre” maior ângulo no mesmo tempo, tendo, portanto maior velocidade angular.
08. Falsa — coroa — R=15cm — catraca — r=15/4=3,75cm — roda — Rr=5.r=5.3,75 —

Rr=18,75cm — fcoroa.R = fcatraca.r — 1.15 = fcatraca.3,75 — fcatraca=4 voltas — enquanto a coroa efetua 1 volta completa, a catraca e a roda efetua efetuam 4 voltas completas — deslocamento da roda após as 4 voltas —S=2πRr=2.3.18,75×4=450cm=4,5m.
16. Correta — roda — Rr=50cm — R=2r — fcoroa.R = fcatraca.r — 2.2r = fcatraca.r — fcatraca=4 voltas — distância percorrida pela roda após essas 4 voltas — S=4×2πRr=8π50=400πcm=4πm — velocidade (pedida) da roda e consequentemente da bicicleta em t=1s — V=S/t=4πm/1s —
V= 4πm/s.
R- (01, 02, 16)
04- Todos os pontos da correia (admitidos inextensíveis) têm a mesma velocidade escalar V que todos os pontos da periferia de cada polia, desde que não ocorra deslizamento— V=W.R — W=2π/T — assim, V1=V2 — W1.R1 = W2.R2 — 2π/T1.R1= 2π/T2.R2 — 2πf1.R1 = 2πf2.R2
![]()
Generalizando— f.R=constante=K — observe que o raio é inversamente proporcional à freqüência (maior raio corresponde à menor freqüência)
Note na montagem P que as polias 1 e 2 estão acopladas e V1 = V2—o mesmo acontece na montagem

ondeV1 = V3— polias que estão fixas no mesmo eixo de rotação possuem a mesma velocidade angular, (“varrem” o mesmo ângulo no mesmo tempo) assim, nas montagens P e Q você tem que W2 = W3
Resumindo:as polias 1 e 3 giram com velocidades lineares iguais em pontos periféricos (V1 = V3) e, pelo enunciado, por questão de segurança, é necessário que a serra possua menor velocidade linear, o que acontece na montagem Q onde a serra de fita está acoplada à polia de menor raio — R- A.
05- Todos os pontos da correia e das periferias (extremidades) das polias B e C possuem a mesma velocidade (escalar, linear, tangencial ) V — VB=VC — relação entre as velocidades angular W e tangencial V — W=V/R — V=WR — WA.RA = WB.RB (I) — mas, as polias que giram em torno do mesmo eixo possuem a mesma velocidade angular W, ou seja, WA=WB, que substituído em (I) fornece — WARB = WCRC — WA=(RC/RB).WC=(10/2)WC — WA=5WC — mas W=∆θ(ângulo varrido)/ ∆t (intervalo de tempo) — assim, enquanto a polia A efetua uma volta completa , no mesmo tempo a polia C efetuará 5 voltas completas — observe então que, se no tempo de desaceleração a polia a polia C efetuar n voltas até parar, a polia A efetuará 5n voltas nesse mesmo tempo — cálculo do número de voltas completas efetuadas pela polia A enquanto está sendo desenrolada pelo fio — comprimento do fio, dado do exercício L=10π m (II) — distância percorrida pela polia A ao efetuar uma volta completa — ∆SA= 2πRA=2π,1=2π m (III) —
Dividindo (II) por (III) você obtém o número de voltas dadas pela polia A até soltar o fio — 10π/2π=5voltas — mas,pós essas 5 voltas ela continua girando até parar efetuando mais 2n voltas — número total de voltas efetuadas pela polia A — nA=5n + 5=5(n + 1) — calculando a aceleração a pela polia A onde o ponto P da corda percorre L=10π m até parar (V=0) com velocidade inicial VA, quando o fio começa a ser puxado — V2=Vo2 + 2.(-a),L —
02=VA2 – 2.(a).10π — VA2=20πa — WA2.RA2=20πa — (5WC)2.12=20πa — WC=WC=2π rad/s (fornecido pelo gráfico da figura 3 — (5.2π)2.12=20πa — 100π2=20πa — a=5π m/s2.
R- A.
06- Como as rodas dentadas estão perfeitamente ajustadas, o número de dentes é proporcional ao

raio de cada roda —fA.RA=fB.RB — fA.144=fB.126 — fA=0,875fB — WA=2πfA — 0,21=2.3.,875fB — fB=0,04Hz — WB=2πfB —WB=2.3.0,04 — WB=0,24rad/s — R- C.
07- O número de dentes é proporcional ao raio de cada roda — fR.RR = fp.Rp — fp=6 voltas

— fR.21=6/t.49 — fR=294/21 — fR=14 voltas completas — enquanto a roda do pedal gira 6 voltas completas, no mesmo tempo a roda traseira gira 14 voltas completas — se, em cada volta completa a roda traseira percorre 1,8m, em 14 voltas percorrerá — ∆S=14.1,8=25,2 voltas — R- D
08- a) Para o portão abrir totalmente ele deve girar um ângulo ∆θ=90o=π/2 rad — W=∆θ/∆t=(π/2)/∆t — ∆t=π/2W.
b) Função horária do MUV — S=So + Vot + at2/2 — D= 0 + 0 + at2/2 — D=a.(π/2W)2/2 — D=a.(π2/4W2)/2 — D= π2a/8W2 — a= 8W2D/π2.
