Cinemática – 2013 – 2014
2013 – 2014
Cinemática
MOVIMENTO UNIFORME
01-(UEL-PR-014)
Analise a figura a seguir.
Os habitantes de metrópoles convivem com o problema dos congestionamentos de automóveis, que geram estresse, acidentes, poluição sonora, entre outras consequências. Uma solução para o problema de mobilidade urbana é o transporte coletivo por linhas de metrô. A figura mostra a região central da cidade de Brasília. Considere que um indivíduo se desloca diariamente de carro da posição A, onde mora, até a posição B, onde trabalha, em um percurso de 12 km representado pela linha tracejada. No horário de rush,
a velocidade média dos automóveis é de 12 km/h e, fora desse horário, é de 42 km/h. Se houvesse em Brasília uma linha de metrô de A até B, como representado pela linha ponto-tracejada, ela teria 20 km.
Supondo que a velocidade média do metrô seja de 60 km/h, considere as afirmativas a seguir
I. No horário de rush, o tempo de deslocamento de carro de A até B é maior do que o tempo de deslocamento por metrô em 1 hora.
II. No horário de rush, o tempo de deslocamento de A até B por metrô é 1/3 do tempo de deslocamento
por carro.
III. Fora do horário de rush, é mais rápido fazer o percurso de A para B de carro.
IV. Fora do horário de rush, considerando que o sistema de metrô tenha melhorado e que sua velocidade
média passe a ser de 70 km/h, então o tempo de deslocamento de A até B tanto por carro quanto por metrô é igual.
Assinale a alternativa correta.
a) Somente as afirmativas I e II são corretas.
b) Somente as afirmativas I e IV são corretas.
c) Somente as afirmativas III e IV são corretas.
d) Somente as afirmativas I, II e III são corretas.
e) Somente as afirmativas II, III e IV são corretas.
02-(PUC-RJ-014)
Um passageiro do metrô no Rio de Janeiro deseja fazer uma viagem da estação Botafogo até a
estação Cinelândia.
A distância e o tempo estimado de viagem entre cada uma das estações da linha do metrô é apresentado na tabela abaixo.
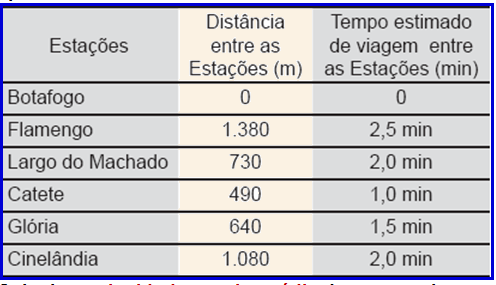
Calcule a velocidade escalar média do passageiro em seu trajeto, em metros por segundo.
(A) 7,8 (B) 8,0 (C) 48,0 (D) 474,7 (E) 480,0
03-(UNICAMP-SP-014)
Andar de bondinho no complexo do Pão de Açúcar no Rio de Janeiro é um dos passeios aéreos urbanos mais famosos do mundo. Marca registrada da cidade, o Morro do Pão de Açúcar é constituído de um único
bloco de granito, despido de vegetação em sua quase totalidade e tem mais de 600 milhões de anos.
O passeio completo no complexo do Pão de Açúcar inclui um trecho de bondinho de aproximadamente 540 m, da Praia Vermelha ao Morro da Urca, uma caminhada até a segunda estação no Morro da Urca, e um segundo trecho de bondinho de cerca de 720 m, do Morro da Urca ao Pão de Açúcar. A velocidade escalar média do bondinho no primeiro trecho é V1= 10,8 km/h e, no segundo, V2= 14,4 km/h. Supondo que, em certo dia, o tempo gasto na caminhada no Morro da Urca somado ao tempo de espera nas estações é de 30 minutos, o tempo total do passeio completo da Praia Vermelha até o Pão de Açúcar será igual a
a) 33 min. b) 42 min. c) 50 min. d) 36 min
04-(UEFS-BA-014)
Em uma corrida de 100 metros rasos, o vencedor completou o percurso, desenvolvendo velocidade
escalar média de 32km/h, enquanto o segundo colocado desenvolveu velocidade escalar média de 30km/h.
No final da corrida, a distância que separava o vencedor do segundo colocado, em metros, era de
A) 5,50 B) 5,75 C) 6,00 D) 6,25 E) 7,802
05-(UFRN-RN-014)
Dois amigos, um residente em Natal (I) e outro em Parnamirim (II), combinaram de ir, cada um no seu automóvel, a um evento na cidade de Goianinha, a 64,0 km de Natal. Apesar de saírem de lugares diferentes, eles pretendiam chegar a Goianinha no mesmo instante. O que mora em Parnamirim, a 8,0 km do ponto de partida do amigo, resolveu sair 6 minutos após o horário combinado para a partida. O gráfico abaixo mostra a posição em função do tempo para os veículos I e II, dirigidos, respectivamente, pelos amigos oriundos de Natal e Parnamirim.
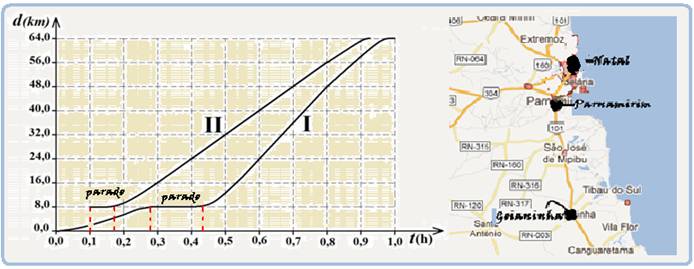
Nessas condições,
A) os veículos pararam durante a viagem? Eles chegaram ao mesmo tempo na cidade? Justifique suas respostas.
B) determine qual dos dois veículos fez o percurso com maior velocidade escalar média.
Justifique sua resposta.
C) considerando que a velocidade máxima permitida no percurso entre Natal e Goianinha é de
100 Km/h, determine se eles cometeram excesso de velocidade durante a viagem. Justifique
sua resposta.
06-(PUCCAMP-SP-014)
Carlos pratica caminhada. Segundo ele, sua velocidade é de 3500 m/h, velocidade aferida com um relógio que adianta exatos um minuto e 40 segundos por hora. Julieta, amiga de Carlos, também pratica a caminhada e diz que sua
velocidade é de 3330 m/h, velocidade medida com um relógio que atrasa exatos um minuto e 40 segundos por hora. Os dois amigos resolveram caminhar partindo juntos do mesmo local, na mesma direção e sentido. Cada um manteve a sua velocidade costumeira. Após uma hora, marcada em um relógio preciso, Julieta estará
(A) atrás de Carlos em 360 metros. (B) atrás de Carlos em 240 metros. (C) junto com Carlos.
(D) adiante de Carlos em 240 metros. (E) adiante de Carlos em 360 metros.
07-(PUCCAMP-SP-013)
A figura indica um avião supersônico voando de A para C a 12 km de altitude e com velocidade constante de 1872 km/h.
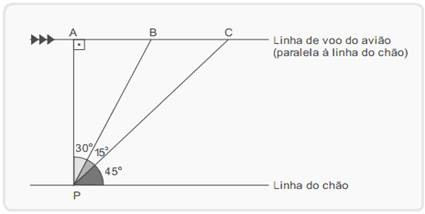
Desprezando-se a curvatura da Terra e adotando no cálculo final √3 =1,7 , o tempo que esse avião leva para ir de B até C, em segundos, é igual a
(A) 6. (B) 8 (C) 10 (D) 12 (E) 14
08-(PUC-RJ-013)
O gráfico da figura mostra a posição em função do tempo
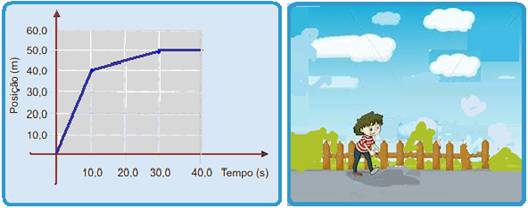
de uma pessoa que passeia em um parque. Calcule a velocidade média em m/s desta pessoa durante todo o passeio, expressando o resultado com o número de algarismos significativos apropriados.
(A) 0,50 (B) 1,25 (C) 1,50 (D) 1,70 (E) 4,00
09-(ENEM-MEC-013)
Uma empresa de transportes precisa efetuar a entrega de uma encomenda o mais breve possível.
Para tanto, a equipe de logística analisa o trajeto desde a empresa até o local de entrega. Ela verifica que o trajeto apresenta dois trechos de distâncias diferentes e velocidades máximas permitidas diferentes. No primeiro trecho, a velocidade máxima permitida é de 80 km/h e a distância a ser percorrida é de 80 km. No segundo trecho, cujo comprimento vale 60 km, a velocidade máxima permitida é de 120 km/h.
Supondo que as condições de trânsito sejam favoráveis para que o veiculo da empresa permitida, qual será o tempo necessário, em horas, para a realização da entrega?
a) 0,7 b) 1,4 c) 1,5 d) 2,0 e) 3,0
10-(ENEM-MEC-013)
Para melhorar a mobilidade urbana na rede metroviária é necessária minimizar o tempo entre estações. Para isso a
administração do metrô de uma grande cidade adotou o seguinte procedimento entre duas estações: a locomotiva parte
do repouso com aceleração constante por um terço do tempo de percurso, mantém a velocidade constante por outro terço e reduz sua velocidade com desaceleração constante no trecho final, até parar.
Qual é o gráfico de posição (eixo vertical) em função do tempo (eixo horizontal) que representa o movimento desse trem?
11-(UNICAMP-SP-013)
Para fins de registros de recordes mundiais, nas provas de 100 metros rasos não são consideradas
as marcas em competições em que houver vento favorável (mesmo sentido do corredor) com velocidade superior a 2m/s. Sabe-se que, com vento favorável de 2m/s, o tempo necessário para a conclusão da prova é reduzido em 0,1s. Se um velocista realiza a prova em 10s sem vento, qual seria sua velocidade se o vento fosse favorável com velocidade de 2m/s?
a) 8,0m/s. b) 9,9m/s. c) 10,1m/s. d) 12,0m/s.
Movimento Uniformemente variado (MUV)
01-(UFJF-MG-014)
A velocidade de um objeto em função do tempo é registrada em um gráfico.
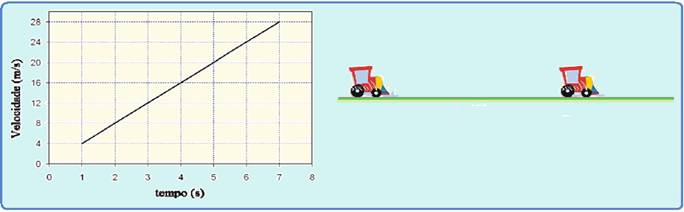
Analisando o gráfico ao lado, determine o módulo da velocidade inicial vo, o módulo da aceleração a e a distância percorrida d entre os instantes t = 3 s e 5 s.
a) vo = 4m/s; a = 4m/s²; d = 4m. b) vo = 4m/s; a = 0m/s²; d = 8m. c) vo = 0m/s; a = 4m/s²; d = 32m.
d) vo = 0m/s; a = 0m/s²; d = 8m. e) vo = 4m/s; a = 4m/s²; d = 32m.
02-(UEL-PR-014)
O desrespeito às leis de trânsito, principalmente àquelas relacionadas à velocidade permitida nas vias
públicas, levou os órgãos regulamentares a utilizarem meios eletrônicos de fiscalização: os radares capazes de aferir a velocidade de um veículo e capturar sua imagem, comprovando a infração ao Código de Trânsito Brasileiro.
Suponha que um motorista trafegue com seu carro à velocidade constante de 30 m/s em uma avenida cuja
velocidade regulamentar seja de 60 km/h. A uma distância de 50 m, o motorista percebe a existência de
um radar fotográfico e, bruscamente, inicia a frenagem com uma desaceleração de 5 m/s2.
Sobre a ação do condutor, é correto afirmar que o veículo
a) não terá sua imagem capturada, pois passa pelo radar com velocidade de 50 km/h.
b) não terá sua imagem capturada, pois passa pelo radar com velocidade de 60 km/h.
c) terá sua imagem capturada, pois passa pelo radar com velocidade de 64 km/h.
d) terá sua imagem capturada, pois passa pelo radar com velocidade de 66 km/h.
e) terá sua imagem capturada, pois passa pelo radar com velocidade de 72 km/h.
03-(FGV-SP-014)
Em alguns países da Europa, os radares fotográficos das rodovias, além de detectarem a
velocidade instantânea dos veículos, são capazes de determinar a velocidade média desenvolvida pelos veículos entre dois radares consecutivos.
Considere dois desses radares instalados em uma rodovia retilínea e horizontal. A velocidade instantânea de certo automóvel, de 1 500 kg de massa, registrada pelo primeiro radar foi de 72 km/h. Um minuto depois, o radar seguinte acusou 90 km/h para o mesmo automóvel.
Com a velocidade crescendo de modo constante, em função do tempo, é correto afirmar que a distância
entre os dois radares é de
(A) 450 m. (B) 675 m. (C) 925 m. (D) 1,075 km. (E) 1,350 km.
04-(FGV-SP-014)
Na função horária S = B·t2 + A, em que S representa as posições ocupadas por um móvel sobre uma trajetória retilínea em função do tempo t, as constantes A e B têm, respectivamente, unidades de medida de
(A) velocidade final e aceleração. (B) posição inicial e aceleração. (C) posição inicial e velocidade final.
(D) aceleração e velocidade inicial. (E) posição e velocidade iniciais.
05-(UNESP-SP-014)
Um motorista dirigia por uma estrada plana e retilínea quando, por causa de obras, foi obrigado a desacelerar seu veículo, reduzindo sua velocidade de 90 km/h (25 m/s) para 54 km/h (15 m/s). Depois de passado o trecho em obras, retornou à velocidade inicial de 90 km/h. O gráfico representa como variou a velocidade escalar do veículo em função do tempo, enquanto ele passou por esse trecho da rodovia.
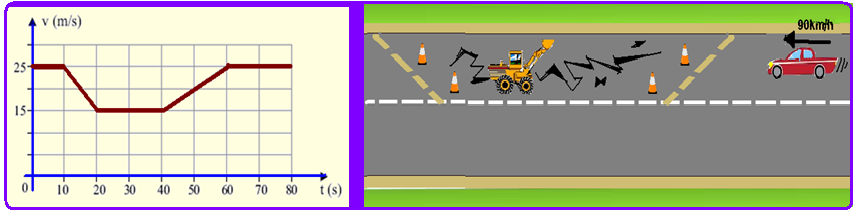
Caso não tivesse reduzido a velocidade devido às obras, mas mantido sua velocidade constante de 90 km/h durante os 80 s representados no gráfico, a distância adicional que teria percorrido nessa estrada seria, em metros, de
(A) 1 650. (B) 800. (C) 950. (D) 1 250. (E) 350.
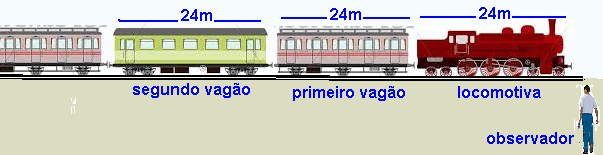
06-(UNIOESTE-PR-014)
Um comboio ferroviário é composto por uma locomotiva e vários vagões. Tanto a locomotiva como os vagões possuem 24 m de comprimento cada um. A locomotiva demora 4,0 s para passar diante de um observador parado próximo aos trilhos e o primeiro vagão demora 2,0 s para passar diante do mesmo observador. Supondo a aceleração constante, assinale a alternativa CORRETA.
A. A aceleração do comboio é igual a 0,50 m.s-2.
B. A velocidade da locomotiva, quando começa a passar diante do observador, é igual a 4,0 m.s-1.
C. O segundo vagão demora 1,0 s para passar diante do observador.
D. Quando o primeiro vagão começa a passar diante do observador, a velocidade do comboio é igual a 36 km.h-1.
E. Quando o segundo vagão começa a passar diante do observador, a velocidade do comboio é igual a 54 km.h-1.
07-(UNIMONTES-MG-013)
Dois carros iniciam, a partir do repouso, uma competição em uma pista de corrida retilínea. O carro 1 arranca 50m à
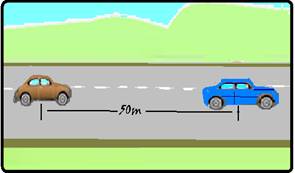
frente do carro 2; ambos se movem com aceleração constante. Se a aceleração mantida pelo carro 2 é duas vezes maior que a do carro 1 (a2 = 2 a1), ele alcançará o carro 1 após percorrer
A) 200m. B) 150m. C) 100m. D) 50m.
08-(UFRN-RN-013)
Após ser conscientizado por uma campanha da Polícia Rodoviária Federal, um motorista deseja saber qual a distância mínima que ele deveria manter de um veículo que trafegasse a sua frente, na mesma direção e sentido, para evitar uma possível colisão caso esse veículo freasse repentinamente, obrigando-o a também frear bruscamente.
Pesquisando na internet, ele encontrou o valor de 0,6 segundos para o tempo de reação de um motorista, isto é, o intervalo de tempo entre ele perceber que o veículo a sua frente freou e o instante em que ele aciona os freios. A figura a seguir ilustra uma situação em que dois veículos de passeio trafegam na mesma direção e sentido.
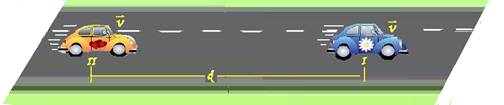
Considere que: os dois veículos estão a 72 km/h (20 m/s); o motorista do veículo I acionou os freios quando o veiculo II se encontrava a uma distância d; e, durante a frenagem, os veículos percorrem a mesma distância. Nessa situação, é correto afirmar:
A) a distância mínima, d, entre os veículos, para que não ocorra colisão, deve ser 20m.
B) a distância mínima, d, entre os veículos, para que não ocorra colisão, deve ser 10m.
C) a distância mínima, d, entre os veículos, para que não ocorra colisão, deve ser 24m.
D) a distância mínima, d, entre os veículos, para que não ocorra colisão, deve ser 12m.
09-(ESPCEX-013)
Um carro está desenvolvendo uma velocidade constante de 72 km/h em uma rodovia federal. Ele passa por um trecho da rodovia que está em obras, onde a velocidade máxima permitida é de 60 km/h. Após 5 s de passagem do carro, uma viatura policial inicial uma perseguição partindo do repouso e desenvolvendo uma aceleração constante. A
viatura se desloca 2,1 km até alcançar o carro do infrator. Nesse momento, a viatura policial atinge a velocidade de
a) 20 m/s b) 24 m/s c) 30 m/s d) 38 m/s e) 42 m/s
10-(UNESP-SP-013)
Dois automóveis estão parados em um semáforo para pedestres localizado em uma rua plana e retilínea. Considere o eixo x paralelo à rua e orientado para direita, que os pontos A e B da figura representam esses automóveis e que as coordenadas xA(0) = 0 e xB(0) = 3, em metros, indicam as posições iniciais dos automóveis.
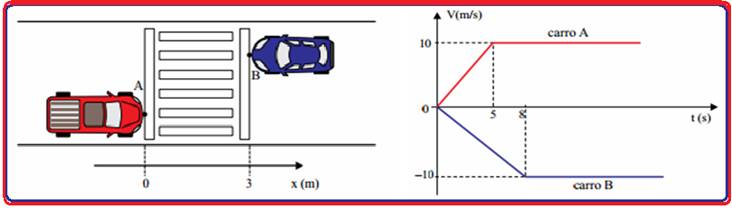
Os carros partem simultaneamente em sentidos opostos e suas velocidades escalares variam em função do tempo, conforme representado no gráfico.
Considerando que os automóveis se mantenham em trajetórias retilíneas e paralelas, calcule o módulo do deslocamento sofrido pelo carro A entre os instantes 0 e 15 s e o instante t, em segundos, em que a diferença entre as coordenadas xA e xB, dos pontos A e B, será igual a 332 m.
Movimentos verticais
01-(UFPR-PR-014)
Considere um edifício em construção, constituído pelo andar térreo e mais dez andares. Um servente de pedreiro deixou cair um martelo cuja massa é 0,5 kg a partir de uma altura do piso do
décimo andar. Suponha que cada andar tem uma altura de 2,5 m e que o martelo caiu verticalmente em queda livre partindo do repouso. Considere a aceleração da gravidade igual a 10 m/s² e o martelo como uma partícula. Despreze a resistência do ar, a ação do vento e a espessura de cada piso.
Levando em conta as informações dadas, analise as seguintes afirmativas:
1. A velocidade do martelo ao passar pelo teto do 1⁰ andar era 20 m/s.
2. A energia cinética do martelo ao passar pelo piso do 5⁰ andar era maior que 100 J.
3. Se a massa do martelo fosse o dobro, o tempo de queda até o chão diminuiria pela metade.
Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira. b) Somente a afirmativa 2 é verdadeira.
c) Somente as afirmativas 1 e 2 são verdadeiras. d) Somente as afirmativas 2 e 3 são verdadeiras.
e) As afirmativas 1, 2 e 3 são verdadeiras.
02-(UDESC-014)
Uma pessoa do alto de um prédio solta uma bola e mede o módulo da posição da bola em função do tempo. A Figura, abaixo, mostra o esboço do gráfico da posição em relação ao tempo.
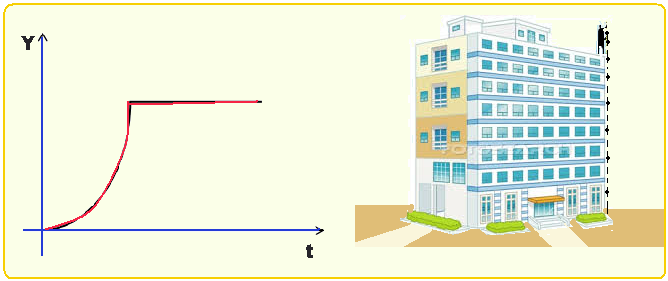
Assinale a alternativa que representa o esboço dos gráficos em relação à velocidade × tempo e
à aceleração × tempo, respectivamente.
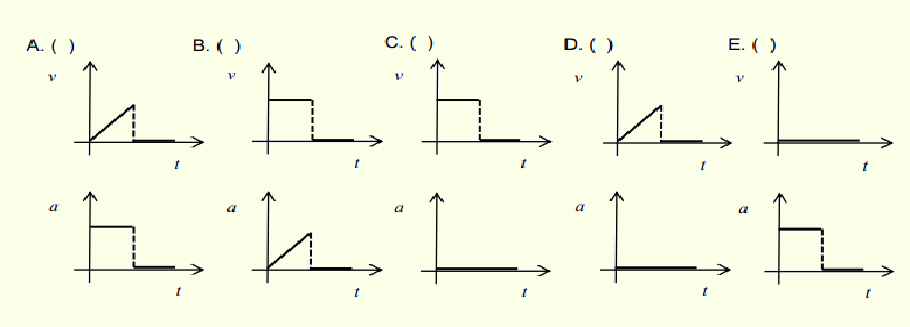
03-(UFSCAR-SP-014)
Para decidir a posse da bola no início de um jogo de futebol, o juiz lança uma moeda verticalmente
para cima e aguarda seu retorno para a palma de sua mão. Dos esboços gráficos abaixo, aquele que pode representar a variação da velocidade escalar do centro de massa da moeda em função do tempo, supondo desprezível a resistência do ar, é
04-(UNESP-SP-014)
Em um dia de calmaria, um garoto sobre uma ponte deixa cair, verticalmente e a partir do repouso, uma bola no instante to=0. A bola atinge, no instante t4, um ponto localizado no nível das águas do rio e à distância h do ponto de lançamento. A figura apresenta, fora de escala, cinco posições da bola, relativas aos instantes to, t1, t2, t3 e t4.
Sabe-se que entre os instantes t2 e t3 a bola percorre 6,25 m e que g = 10 m/s2.
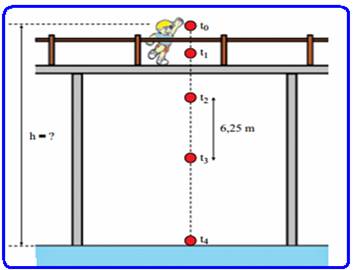
Desprezando a resistência do ar e sabendo que o intervalo de tempo entre duas posições consecutivas apresentadas na figura é sempre o mesmo, pode-se afirmar que a distância h, em metros, é igual a
(A) 25. (B) 28. (C) 22. (D) 30. (E) 20.
Lançamento obliquo
01-(FGV-SP-014)
A distância horizontal percorrida por um dardo, denotada por d e dada em metros, pode ser calculada aproximadamente pela fórmula d=Vo2.sen(2α)/10, sendo Vo a velocidade inicial do dardo, em metros por segundo, e α o ângulo do lançamento.
a) Calcule a velocidade inicial (em m/s) de lançamento de um dardo que atingiu a distância de 80 metros ao ser lançado sob um ângulo de 15º.
b) O recorde mundial masculino da prova de lançamento do dardo foi estabelecido em 1996 por Jan Zelezny, com a marca de 98,48 m. Admitindo-se que o lançamento tenha sido feito com o melhor ângulo possível, e usando 98 m nos cálculos, determine a velocidade inicial do dardo de Jan Zelezny no lançamento. Entregue o resultado em km/h.
b) Pelo enunciado, o melhor ângulo possível ocorre quando o alcance é máximo e, o maior valor para sen (2α) o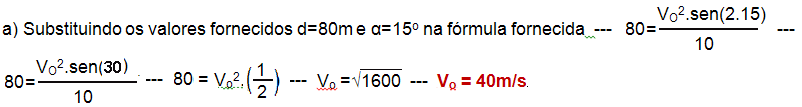
corre quando α=45o, pois sen(2α)=sen(2.45o)=sen90o=1 — 98=Vo2.1 10 — Vo=√980≈31msx3,6 —
Vo ≈ 111km/h
02-(FGV-SP-014)
Na superfície lunar, uma pequena bola lançada a partir do solo com velocidade inicial inclinada de 45o com a horizontal voltou ao solo 8,0 m adiante do ponto de lançamento. A velocidade inicial, em metros por segundo, e o tempo de permanência dela em movimento, em segundos, foram, respectivamente,
03-(UEFS-BA-014)
Um goleiro chuta uma bola, que se encontra parada no gramado, para um jogador situado a 57,0m da
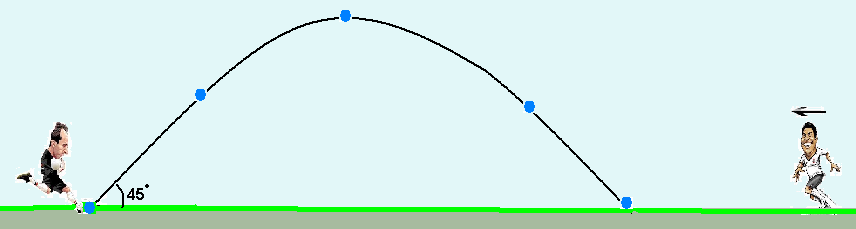
posição do goleiro. A bola é lançada com velocidade de 20,0m/s, fazendo um ângulo de 45° com o plano horizontal.
Desprezando-se a resistência do ar, considerando-se o módulo da aceleração da gravidade local igual a 10,0m/s2 e sabendo-se que sen45° = cos45° = √2/2, o módulo da velocidade do jogador para alcançar a bola, no instante em que ela toca o gramado, em m/s, deve ser de, aproximadamente,
A) 4,0 B) 5,0 C) 6,0 D) 7,0 E) 8,0
04-(UPF-RS-014)
Questão 50 – Considere um vagão deslocando-se em uma trajetória retilínea com velocidade constante e igual a 5 m/s. Um observador, A, dentro dele, lança uma pedra verticalmente para cima. Um outro observador, B, do lado de fora do vagão e em repouso em relação à Terra, observa o vagão passar. Sendo VA e VB , respectivamente, as velocidades da pedra no ponto mais alto de sua trajetória em relação a cada observador, pode-se concluir que:
a) VA = 0 e VB = 0 b) VA = 0 e VB = 5 m/s c) VA = 5 m/s e VB = 0 d) VA = 5 m/s e VB = 5m/s
e) VA = 0 e VB = 10 m/s
05-(UFAM-AM-014)
Uma bola de futebol com 450 g de massa, inicialmente em repouso, é chutada obliquamente para cima com velocidade inicial de 20m/s. A bola atinge altura máxima de 10m e atinge uma parede
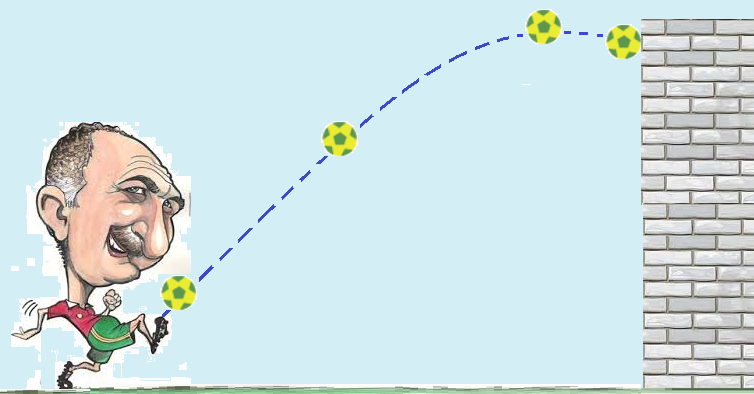
vertical 2s após o chute. Desprezando a resistência do ar, podemos afirmar que a distância do ponto de lançamento da bola até a parede é aproximadamente igual a:
a) 40m b) 28m c) 20m d) 10m e) 14m
06-(PUC-RJ-013)
Um projétil é lançado com uma velocidade escalar inicial de 20 m/s com uma inclinação de 30o com a horizontal,
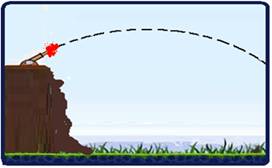
estando inicialmente a uma altura de 5,0 m em relação ao solo.
A altura máxima que o projétil atinge, em relação ao solo, medida em metros, é: Considere a aceleração da gravidade g = 10 m/s2
(A) 5,0 (B) 10 (C) 15 (D) 20 (E) 25
07-(UNIFESP-SP-013)
O atleta húngaro KrisztianPars conquistou medalha de ouro na olimpíada de Londres no lançamento de martelo. Após girar sobre si próprio, o atleta lança a bola a 0,50 m acima do solo, com velocidade linear inicial que forma um ângulo de 45º com a horizontal. A bola toca o solo após percorrer a distância horizontal de 80 m.
Nas condições descritas do movimento parabólico da bola, considerando a aceleração da gravidade no local igual a 10 m/s2, √2 igual a 1,4 e desprezando-se as perdas de energia mecânica durante o vôo da bola, determine,
aproximadamente:
a) o módulo da velocidade de lançamento da bola, em m/s.
b) a altura máxima, em metros, atingida pela bola.
08-(MACKENZIE-SP-013)
Uma bola de futebol, ao ser chutada por um garoto, sai do solo com velocidade de 30,0 m/s, formando um ângulo de
60º acima da horizontal. Desprezando a resistência do ar, a velocidade da bola no ponto mais alto da trajetória será de
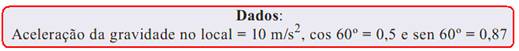
a) 11,1 m/s b) 15,0 m/s c) 18,0 m/s d) 26,1 m/s e) 30,2 m/s
09-(PUC-RS-013)
Uma esteira horizontal despeja minério dentro de um vagão. As pedras de minério saem da esteira com velocidade
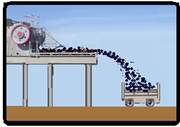
horizontal de 8,0m/s e levam 0,60s numa trajetória parabólica até o centro do vagão. Considerando o peso como força resultante atuando em cada pedra e a aceleração da gravidade como 10m/s2, os módulos dos deslocamentos horizontal e vertical, bem como o da velocidade das pedras quando chegam ao vagão são, respectivamente,
A) 6,0m; 6,0m e14m/s B) 6,0m; 4,8m e 14m/s C) 4,8m; 3,6m e 10m/s D) 4,8m; 1,8m e 10m/s
E) 4,8m; 1,8m e 6,0m/s
10-(UNIOESTE-PR-013)
Um canhão atira projéteis com velocidade de 100 m.s-1 num local plano e horizontal onde a aceleração da gravidade é
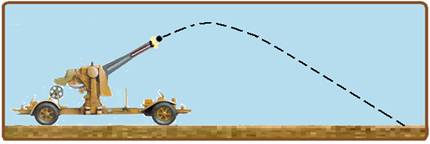
igual a 10 m.s-2. Se o ângulo θ de lançamento, com a horizontal, é tal que senθ=0,6 e desprezando a resistência do ar, assinale a alternativa correta.
A. A componente horizontal da velocidade dos projéteis é igual a 60 m.s-1.
B. A componente vertical da velocidade do projétil é igual a 80 m.s-1.
C. Os projéteis atingem o chão num ponto localizado a 480 m do canhão.
D. Os projéteis atingem uma altura máxima igual a 360 m.
E. Os projéteis permanecem no ar durante 12 s.
MOVIMENTO CIRCULAR
01-(UNICAMP-SP-014)
As máquinas cortadeiras e colheitadeiras de cana-de-açúcar podem substituir dezenas de trabalhadores 
rurais, o que pode alterar de forma significativa a relação de trabalho nas lavouras de cana-de-açúcar. A pá
cortadeira da máquina ilustrada na figura abaixo gira em movimento circular uniforme a uma frequência de 300 rpm.
A velocidade de um ponto extremo P da pá vale (Considere 
=3)
a) 9 m/s. b) 18 m/s. c) 15 m/s. d) 60 m/s.
02-(UERJ-RJ-014)
Uma máquina possui duas engrenagens circulares, sendo a distância entre seus centros A e B igual
a 11 cm, como mostra o esquema:
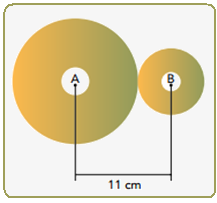
Sabe-se que a engrenagem menor dá 1000 voltas no mesmo tempo em que a maior dá 375 voltas, e que os comprimentos dos dentes de ambas têm valores desprezíveis.
A medida, em centímetros, do raio da engrenagem menor equivale a:
(A) 2,5 (B) 3,0 (C) 3,5 (D) 4,0
03-(UEM-PR-014)
32
Um modelo padrão para dar movimento a uma bicicleta consiste em duas polias conectadas por uma
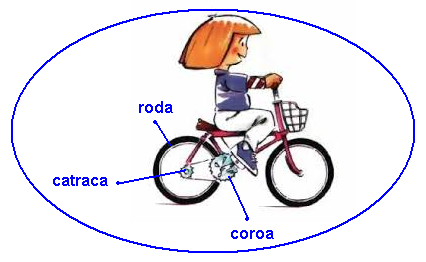
corrente.
Uma das polias, chamada de coroa, fica conectada aos pedais, enquanto a outra polia, chamada de catraca, fica acoplada à roda traseira da bicicleta. Cada pedalada, isto é, cada giro completo dos pedais, corresponde a um giro completo da coroa, enquanto cada volta completa da catraca corresponde a uma volta completa da roda à qual está acoplada. Sabe-se, ainda, que o número de voltas da catraca é proporcional ao número de voltas da coroa, com razão de proporção igual à razão entre os raios da coroa (R) e da catraca (r). Considerando que a bicicleta, a partir do modelo apresentado, desloca-se em linha reta em uma superfície plana e que não haja deslizamento entre as rodas da bicicleta e a superfície, assinale o que for correto.
01) Se os raios da coroa e da catraca são, respectivamente, R e r, então cada volta completa da
coroa corresponde a R/r voltas da catraca.
02) Para um dado R fixo, quanto menor for o raio da catraca, maior será o deslocamento da bicicleta por pedalada realizada.
04) As velocidades angulares da coroa e da catraca são sempre iguais, independentemente do valor de seus raios.
08) Se a coroa de uma bicicleta tem raio igual a 15 cm, e a catraca tem raio igual a 1/5 do raio da roda e 1/4 do raio da coroa, então cada pedalada corresponde a um deslocamento de 1,5 m.
16) Se as rodas de uma bicicleta têm raio igual a 50 cm e se o raio da coroa é o dobro do raio da catraca, então um ciclista que realiza duas pedaladas por segundo nessa bicicleta movimenta-se a 4πm/s.
04-(ENEM-MEC-013)
Para serrar ossos e carnes congeladas, um açougueiro utiliza uma serra de fita que possui três polias e um
motor. O equipamento pode ser montado de duas formas diferentes, P e Q. Por questão de segurança, é necessário que a serra possua menor velocidade linear.
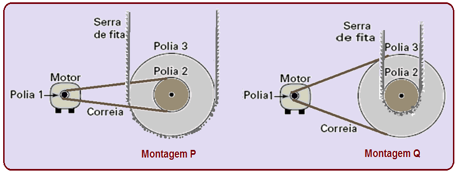
Por qual montagem o açougueiro deve optar e qual a justificativa desta opção?
A) Q, pois as polias 1 e 3 giram com velocidades lineares iguais em pontos periféricos e a que tiver maior raio terá menor frequência.
B) Q, pois as polias 1 e 3 giram com frequências iguais e a que tiver maior raio terá menor velocidade linear
em um ponto periférico.
C) P, pois as polias 2 e 3 giram com frequências diferentes e a que tiver maior raio terá menor velocidade
linear em um ponto periférico.
D) P, pois as polias 1 e 2 giram com diferentes velocidades lineares em pontos periféricos e a que tiver menor raio terá maior frequência.
E) Q, pois as polias 2 e 3 giram com diferentes velocidades lineares em pontos periféricos e a que tiver maior raio terá menor frequência
05-(AFA-013)
A figura 1 abaixo apresenta um sistema formado por dois pares de polias coaxiais, AB e CD, acoplados por meio de
uma correia ideal e inextensível e que não desliza sobre as polias C e B, tendo respectivamente raios RA=1 m, RB = 2 m , RC = 10 m e RD = 0,5 m.
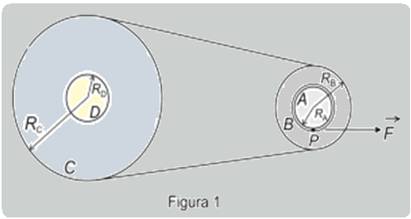
A polia A tem a forma de um cilindro no qual está enrolado um fio ideal e inextensível de comprimento L=10π m em
uma única camada, como mostra a figura 2.
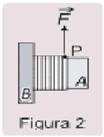
Num dado momento, a partir do repouso, o fio é puxado pela ponta P, por uma força F constante que imprime uma
aceleração linear a, também constante, na periferia da polia A, até que o fio se solte por completo desta polia. A partir
desse momento, a polia C gira até parar após n voltas, sob a ação de uma aceleração angular constante de tal forma que
o gráfico da velocidade angular da polia D em função do tempo é apresentado na figura 3.
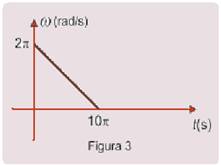
Nessas condições, o número total de voltas dadas pela polia A até parar e o módulo da aceleração a, em m/s2, são,
respectivamente,
a) 5(n + 1), 5π b) 5n, 5π c) 2(n – 1), 3π d) 5n, π
06-(PUCCAMP-SP-013)
As rodas dentadas constituem engrenagens úteis para a transmissão de movimento. Duas rodas
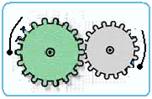
dentadas perfeitamente ajustadas são denominadas A e B. Enquanto a roda A, de 144 dentes, gira em torno de seu eixo com velocidade angular de 0,21 rad/s, a roda B, de 126 dentes, tem velocidade angular em torno de seu eixo, em rad/s, de
(A) 0,18. (B) 0,21. (C) 0,24. (D) 0,28. (E) 0,31.
07-(PUCCAMP-013)
A roda dentada acoplada aos pedais de uma bicicleta possui 49 dentes. Essa roda está ligada, por meio de uma corrente, a uma outra roda dentada, acoplada à roda traseira da bicicleta, e que possui 21 dentes. Desconsiderando qualquer tipo
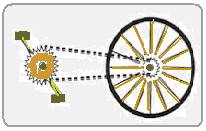
de deslizamento do pneu da bicicleta no chão e considerando apenas o movimento da bicicleta gerado pelas pedaladas, uma pessoa que pedalar o suficiente para que a roda dentada acoplada aos pedais gire 6 voltas completas, fará com que a bicicleta, cujas rodas têm comprimento aproximado de 1,8 m, percorra a distância, em metros, de, aproximadamente,
(A) 6. (B) 15. (C) 20. (D) 25. (E) 32.
08-(UFV-MG-013)
A figura ao lado ilustra um automóvel parado num estacionamento, com sua frente voltada para o portão de saída, que funciona por controle remoto. O motorista, ao dar partida no veículo, aciona no mesmo instante o controle remoto do portão, que passa a abrir-se, girando em torno de seu eixo com velocidade angular constante W.
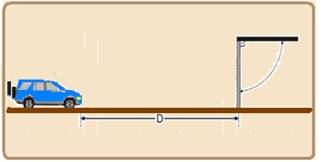
O automóvel, que se encontra à distância D do portão, move-se com aceleração constante de módulo a após a partida, atingindo a saída no mesmo instante em que o portão atinge sua abertura total.
A partir dos dados e informações acima, faça o que se pede:
a) Expresse, em termos de W, o tempo gasto pelo portão para se abrir totalmente.
b) Expresse a aceleração do automóvel em termos de W e D.