Resolução Comentada – Física Térmica – 2017 – 2016 – 2015

Resolução Comentada – Vestibulares Recentes

Física Térmica – 2017 – 2016 – 2015

01-

R- D

03- (V) Temperatura grandeza física que representa a medida do estado de agitação médio das moléculas de um corpo.

(F) Calor energia térmica que passa, de forma espontânea, do corpo demaior temperatura para o de menor temperatura.

(F) Fusão mudança de estado físico sofrida por um sólido ao se transformar em líquido quando recebe uma certa quantidade de calor.

(V ) Evaporação passagem do estado líquido para o estado gasoso que ocorre de forma lenta.

(F) Equilíbrio térmico condição física na qual dois ou mais corpos ficam com a mesma temperatura (temperatura de equilíbrio térmico). As trocas de calor podem não cessar, e os corpos podem continuar recebendo e cedendo calor na mesma proporção.

(V ) Convecção processo de transmissão de calor que ocorre devido à movimentação de massas, em especial, nos líquidos e nos gases e essa movimentação ( massas mais quentes, menos densas sobem e as frias mais densas descem). Essa movimentação ocorre até que a massa total fique com a mesma temperatura.

(F) Caloria quantidade de calor necessária para que 1g de água tenha sua temperatura alterada em 1°C .

R- D

04- I. As prateleiras de uma geladeira doméstica são grades vazadas, para facilitar fluxo de energia térmica até o congelador por […]

Situação I Convecção

II. O único processo de troca de calor que pode ocorrer no vácuo é por […].

Situação II Radiação

III. Em uma garrafa térmica, é mantido vácuo entre as paredes duplas de vidro para evitar que o calor saia ou entre por [….].

Situação III Condução

O calor é conduzido de um ponto a outro do corpo sem que haja deslocamento das partículas.

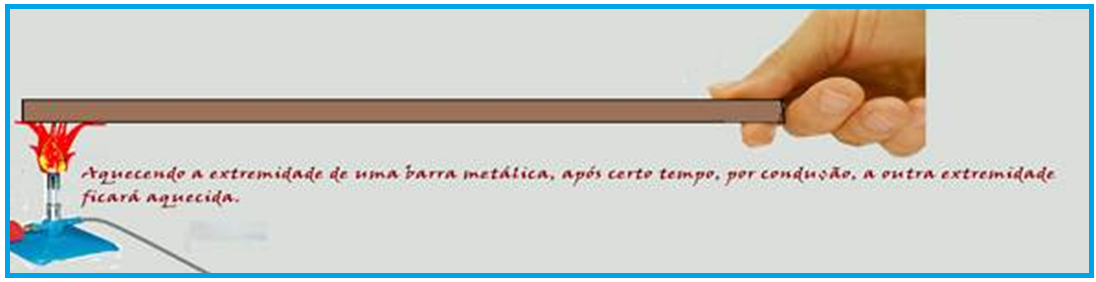
Explicando microscopicamente o fenômeno: a região próxima da chama tem o movimento vibratório de suas moléculas aumentado, adquirindo assim maior energia cinética, que é transferida através de choques às partículas vizinhas, que também aumentam seu movimento vibratório.

Através desse transporte de energia, toda a barra é aquecida.

A condução não ocorre no vácuo, pois ela precisa de um meio material para se propagar.

Na garrafa térmica, é mantido o vácuo entre as paredes de vidro para evitar trocas de calor por condução e convecção.

R- D

05-

Relação entre as escalas Celsius e Fahrenheit = = = 9C = 540 C = 60oC.

R- C

06-

07-

Como toda energia emitida pelo rádio foi absorvida pela água e empregada exclusivamente para elevar sua temperatura sempre no estado líquido indo do ponto de congelamento (0 oC) até o ponto deebulição (100 oC), a energia liberada pelo rádio foi de Q = m.c.(θ – θ_o) = 1,3.1.(100 – 0)

Q = 130 cal.

Como o experimento durou ∆t = 1 h = 3600 s, a potência média liberada pelo rádio é fornecida por

P = = = 0,14 W

R- C

08-

09-

Calor Latente

O calor recebido por um corpo pode fazer com que sua temperatura aumente ou que ele sofra uma mudança de estado. No segundo caso você tem uma quantidade de calor latente, ou seja, o calor latente se refere à quantidade de calor que um corpo recebe apenas para mudar de estado, o que ocorre à temperatura constante.

Constata-se que a quantidade de calor latente (Q) cedida ou retirada de uma substância para que ela mude de estado o que sempre ocorre à temperatura constante é diretamente proporcional à sua massa (m), e depende das características da substância (L). Matematicamente:

O calor de fusão ou de vaporização L é característica do material de que o objeto é feito independendo da massa ou do volume do objeto. Assim, se o objeto possui calor de fusão LF = 50 J/kg ele terá sempre esse valor independente de sua massa ou volume, pois o material é o mesmo.

R- C

10-

11- a) a quantidade de calor, em cal, necessária para elevar a temperatura do copo com água líquida de 20 ºC para 50 ºC.

Copo Q_c para a temperatura do copo subir de t_o = 20^o C para t = 50º C, sendo o calor específico do copo c_c = 0,2 cal/g^oC e m_c = 200 g Qc = mc.c.(t – to) =100.0,2.(50 – 20) Qc = 600 cal.

Água Q_a para a temperatura da água subir de to = 20^oC para t = 50º C, sendo o calor específico da c_a = 1 cal/g^oC e m_a = 100 g Q_a = ma.c_a.(t – t_o) = 200.1.(50 – 20) Q_c = 6000 cal.

Quantidade de calor pedida Qt = 600 + 6000 Qt = 6600 cal.

b) a massa de vapor de água, em gramas, necessária para elevar a temperatura do copo com água líquida até atingir o equilíbrio térmico a 50 ºC.

Pelo enunciado a temperatura inicial do vapor de água era t_o = 120 ^oC,que deve se transformar em água líquida a 50 ^oC. Etapas:

1^a Q₁ quantidade de calor cedida pelo vapor de água para passar de to = 120º C para t = 100º C, sem mudança de estado Q₁ = mv.cv.(t – t_o) = mv.0,5.(100 – 120) Q₁ = – 10mv.

2ª Q₂ quantidade de calor cedida pelo vapor de água para passar devapor de água a 100º C a água líquida a 100º C (condensação, liquefação) Q₂ = mv.L= mV.(-540) Q₂ = – 540mv.

3^a Q₃ quantidade de calor cedida pela água líquida para passar de t_o = 100º C para t = 50º C, sem mudança de estado Q₃ = mv.c_a.(t – to) = mv.1.(50 – 100) Q₃ = – 50mv.

Quantidade de calor cedida pelo vapor de água para se transformar em água líquida a 50oC

Q’ = Q1 + Q2 + Q3 = – 10 mv – 540mv – 50mv Q’ = – 600mv.

Essa quantidade de calor Q’ cedida pelo vapor de água para ir de 120º C a água a 50º C é a mesma recebida pelo sistema (copo + água) para ir de 20º C a 50º C (achada no item Qt = 6600 cal), ou seja, no equilíbrio térmico a soma dessas quantidades de calor trocadas entre o vapor e o copo com água deve ser nula.

– 600mv + 6600 = 0 mv = 6600/600 mv = 11 g.

12- As alternativas (A) e (E) estão erradas, pois a temperatura de fusão ou de vaporização não depende da massa do corpo, apenas do material que o constitui.

A (C) também está errada, pois a substância não é a água que sofre fusão a 0^o C.

Na fusão desse corpo de massa m = 20 g que ocorre a 50 ^oC você deve usar a expressão o calor latente fornecida por Q = m.LF (200 – 100) = 20LF LF = LF = 5 cal/g.

R- D

13- Cálculo da quantidade de calor (energia térmica) necessária para aquecer o líquido de calor específico c = 0,58 cal/g^oC com sua temperatura variando de 0o até 78^oC, sem mudança de estado Q₁ =m.c.(t – t_o) = m.0,58.(78 – 0) Q₁ = 45,24.m.

14- Para resolver esse exercício, precisamos encontrar a massa de água, então vamos utilizar as outras informações que já temos:

Analisando pela quantidade de calor:

Onde:

Q é a quantidade de calor

m é a massa

c é o calor específico

ΔT é a variação de temperatura

Isolando o m:

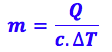Substituindo os valores:

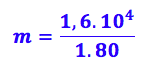Como todos os valores estão em gramas, então nosso resultado vai sair em gramas:

Agora que temos a massa, podemos usar a outra fórmula de quantidade de calor, para calcularmos a vaporização:

Onde:

Q é a quantidade de calor

m é a massa

L é o calor latente de vaporização

R – C

15-

Calculando a massa de leite densidade do leite = mL = dL.VL mL = 1 (g/mL).VL(g) mL = VL (g)

Calculando a massa de café densidade do café = mc = dc.Vc mc = 1g/mL.30 mL mc = 30 g

Após a mistura ambos terão a mesma temperatura (de equilíbrio térmico) = 40 ^oC.

R- B

16-
Princípio das trocas de calor

Colocando vários corpos a diferentes temperaturas no interior de um recipiente adiabático, haverá trocas de calor entre eles, até atingirem o equilíbrio térmico.

Assim, como o recipiente é adiabático, a quantidade de calor cedida pelos corpos mais quentes éigual à quantidade de calor recebida pelos mais frios.

Princípio da Conservação da energia

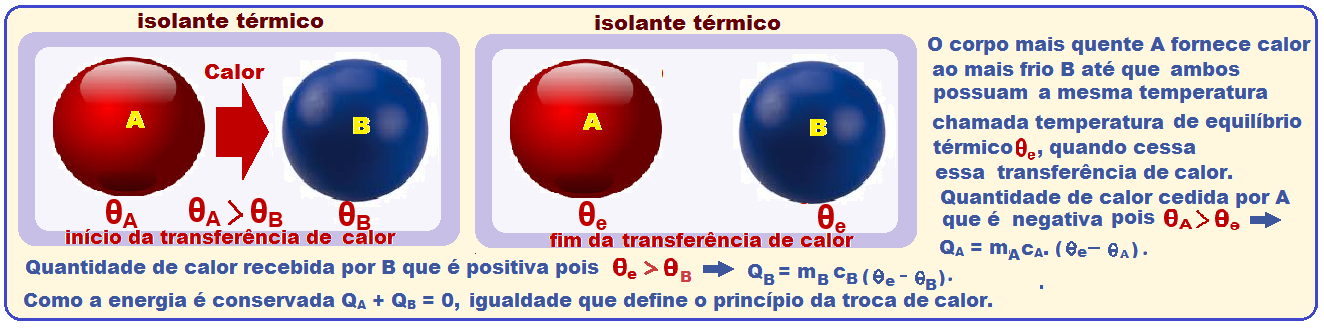
A teoria acima é válida para mais de um corpo e, como a quantidade de calor recebida é positiva e a cedida é negativa, tem-se que Q1 + Q2 + Q3 + …. + QN = 0 ou m1 .c1 .(θe – θ1 ) + m2.c2.( θe – θ2) + m3.c3.( θe –θ3) + … + mN.cN.( θe – θN) = 0.

Enunciado desse princípio das trocas de calor:

Seis horas depois, abre-se a garrafa e mede-se a temperatura da água, obtendo-se θ = 16°C.

R- D

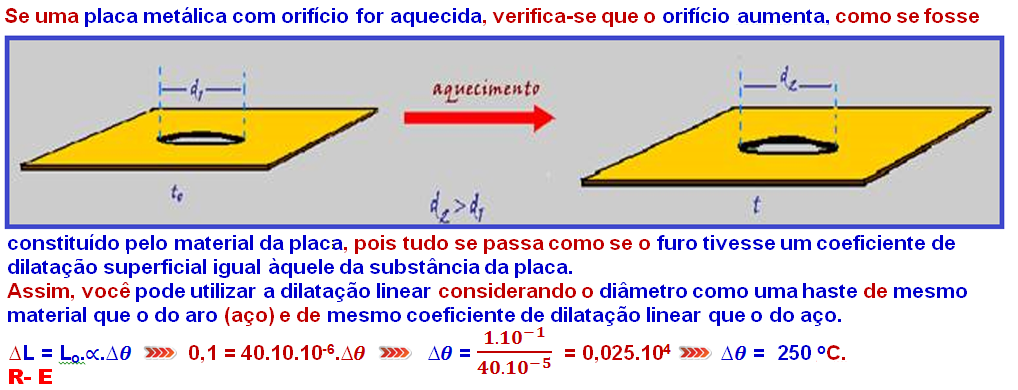
17- Trata-se de dilatação superficial (uma das áreas) fornecida pela expressão a seguir:

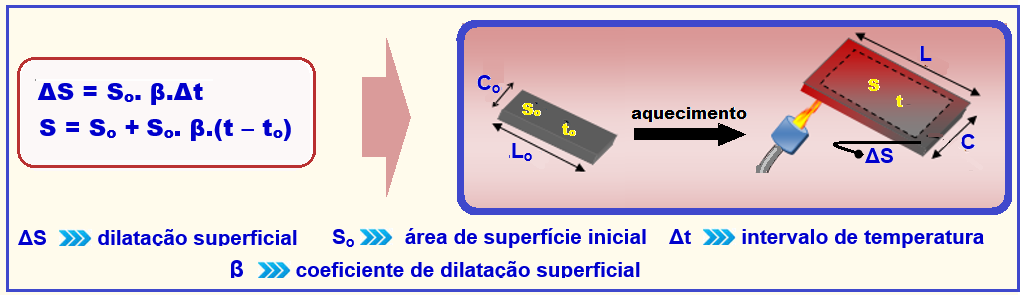
Na expressão acima, a letra grega β (beta) é uma grandeza constante, característica do material, denominada coeficiente de dilatação superficial médio.

Valor de uma das áreas S_o = L_o.L_o = 20×20 = 400 cm² β = 2. = 2.2.10-5 = 4.10^-5 ^oC^-1.

∆S = S_o.β.(t – t_o) = 400.4.10^-5.(120 – 20) = 160000.10^-5 ∆S = 16.10^-1 cm².

R- D

18- Já que o enunciado afirma que o coeficiente de dilatação do vidro utilizado é desprezível comparado ao do álcool, você deve levar em conta apenas a dilatação (∆V) do álcool de coeficiente de dilatação volumétrica = 11.10^-4 ^oC^-1, cujos volume é o do bulbo V_o = 2 cm³, pois ele é totalmente preenchido com álcool até a base do tubo. A variação de temperatura é de ∆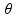 = 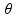– 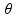_o = 80 – 30 = 50 ^oC.

Substituindo esses valores na expressão da dilatação volumétrica ∆V = Vo. = 2.11.10 ^-4.50 ∆V = 1100.10^–⁴ = 0,11 cm³.

Mas, o volume do cilindro que constitui o tubo é fornecido por ∆V = área da basexaltura = 1.10^-2.h.

O volume de líquido dilatado preenche esse cilindro até a altura h de ∆V = 1.10^-2 .h 0,11 = 0,01h h = h = 11,0 cm.

R – B

19-

20-

Capacidade térmica (C) – Calor específico (c)

Define-se capacidade térmica (C) ou capacidade calorífica de um corpo como sendo o produto da massa desse corpo pelo calor específico da substância de que ele é constituído, ou seja C = m.c como Q = m.c.Δθ Q = C.Δθ ou Q = C.(θ – θ_o).

No caso do exercício Q = C. = (I).

A dilatação térmica (variação de volume ∆V) sofrida pelo bloco é fornecida por ∆V = V_o. ., onde o coeficiente de dilatação volumétrica vale 3. sendo o coeficiente de dilatação linear do bloco ∆V = Vo. . (II).

Substituindo (I) em (II) ∆V = V_o. . .

Portanto, a variação de volume ∆V do bloco é diretamente proporcional a V_o, e inversamente proporcional a C.

R- B

21-

Dilatação linear dos sólidos

Trata-se da dilatação de uma das dimensões de um corpo, como por exemplo, seu comprimento. Considere uma haste metálica de comprimento L_o e à temperatura t_o. Quando aquecida terá comprimento L a uma temperatura t.

Características:

A dilatação linear ΔL é diretamente proporcional à variação de temperatura Δt.

A dilatação linear ΔL é diretamente proporcional ao comprimento inicial Lo.

A dilatação linear ΔL depende do material de que é constituído o corpo.

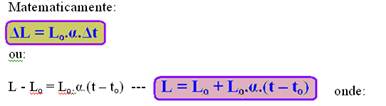
ΔL dilatação linear

α coeficiente de dilatação linear médio, característica do material que constitui a barra.

Lo comprimento inicial

L comprimento final

Δt intervalo de temperatura

Analisando as alternativas:

a) num dia de verão em que a temperatura variar 20 °C o comprimento de uma barra de ferro de 10,0 m sofrerá uma variação de 2,6 cm

a – Falsa

ΔL = Lo.α. Δt

ΔL = 10.13.10^-6.20

ΔL = 26. 10^-4 m = 0,26 cm

b) o coeficiente de dilatação superficial do ferro é 169.10^-6 ^oC^-1.

b – Falsa

 = 2.α  = 2. 13.10^-6 ºC^-1  = 26.10^-6 ºC^-1

c) para cada 1 °C de variação de temperatura, o comprimento de uma barra de 1,0 m desse material varia 13.10^-6m⋅

c – Verdadeira

ΔL = Lo.α. Δt ΔL = 1.13.10-6.1 ΔL = 13.10^-6 m

d) o coeficiente de dilatação volumétrica do ferro é 39.10^-18 ^oC^-1.

d – Falsa

 = 3.α  = 3.13.10^-6  = 39.10-6 ºC^-1

R- C

22-

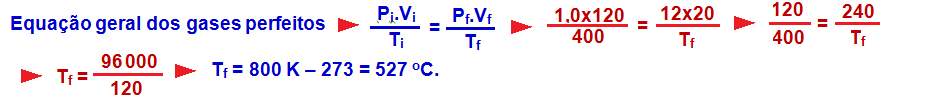
R- C

23-

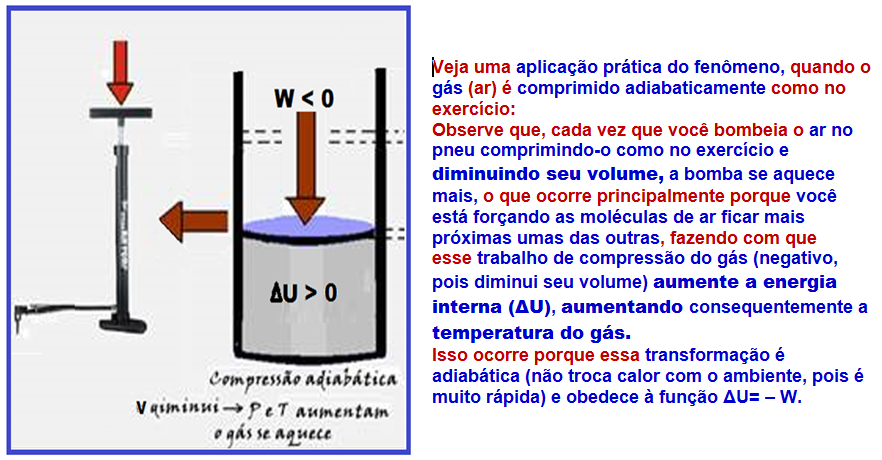
Transformação adiabática

Nela, o sistema não troca calor com o meio externo (Q = 0) e isso ocorre porque o gás está termicamente isolado ou porque a transformação é muito rápida de modo que qualquer troca de calor com possa ser considerada.

Se Q = 0 ΔU = Q – W ΔU = 0 – W ΔU = – W.

R- D

24-

R- A

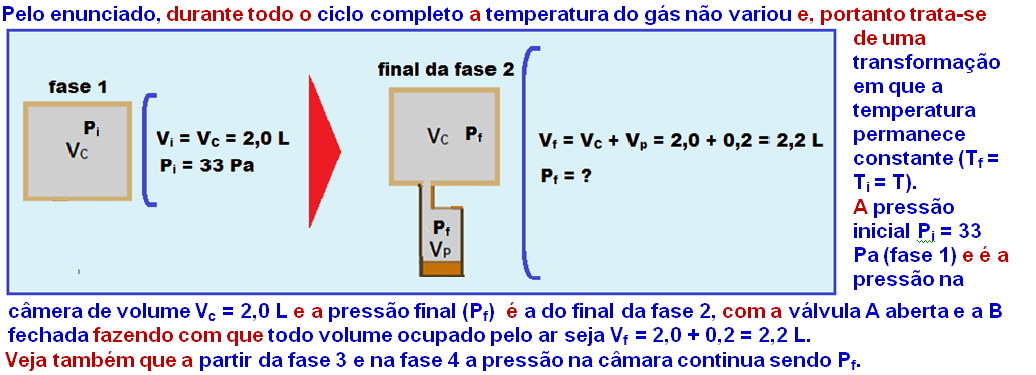
25- Para calcularmos a temperatura final precisamos primeiro do volume final. Podemos calcular visto que sabemos que o êmbolo se deslocou 10 cm:

Volume inicial = 6.10^-3 m³

Volume final = Volume inical + (volume com 10 cm de deslocamento)

Passando 10 cm para metros (dividir por 100):

10 cm = 0,1 m

Calculando :

= área interna X deslocamento

Substituindo:

= 2.10^-2.0,1

Calculando:

= 2.10^-3 m³

Agora calculando o volume final:

Volume final = 6.10^-3 + 2.10^-3

Volume final = 8.10-3 m³

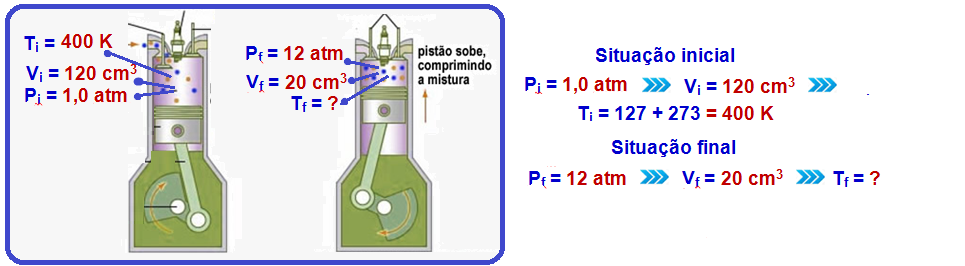
Sabendo o volume final podemos utilizar a fórmula a seguir, já que se trata de um gás ideal:

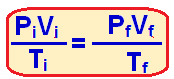
Onde:

Pi e Pf é a pressão inicial e final

Vi e Vf é o volume inicial e final

Ti e Tf é a temperatura inicial e final

Como é uma expansão isobárica (pressão constante) podemos cortar a pressão em ambos os lados, restando apenas:

Substituindo:

Isolando a temperatura final:

Tf =

Calculando:

Tf = 400 K (temperatura final)

Achamos a temperatura, agora vamos para a segunda parte do exercício. Para calcularmos a quantidade de calor vamos utilizar a primeira lei da termodinâmica. Como se trata de uma transformação isobárica:

Como a pressão é constante o nosso trabalho só depende da variação do volume:

W = P.

Substituindo. Nós calculamos a variação anteriormente (2.10^-3):

W = 2.10⁵. 2.10^-3

Calculando:

W = 4.10² J

O exercício já nos forneceu a variação de energia interna (600 J). Vamos então substituir na equação da primeira lei:

= Q – W

Isolando a quantidade de calor:

Q = + W

Substituindo:

Q = 600 + 400

Calculando:

Q = 1000 J (quantidade de calor)

26-

A) A energia interna de certa massa de um gás perfeito é função exclusiva da temperatura desse gás

Aumento de temperatura (ΔT > 0) aumento de energia interna (ΔU > 0).

Diminuição de temperatura (ΔT < 0) diminuição de energia interna (ΔU<0).

Temperatura constante (ΔT = 0) energia interna constante (ΔU = 0).

Vamos então calcular a variação da energia interna em cada transformação:

I: E = 1.105.0,6/TE = 3.105.0,2/TF 6.104 / TE = 6.104/TF TE = TF energia interna constante.

II: F 3.105.0,2/TF = 6.105.0,6/TH 6.104/TE = 6.104/TF 6.104TG = 12.104TF TF > TG TG = 2TF energia interna não constante.

III: G 6.105.0,2/TG = 4.105.0,6/TH 12.104/TG = 24.104/TH 24.104TG= 12.104TH TH = 2TH TH TG energia interna não constante.

IV: H 4.105.0,2/TH = 1.105.0,6/TE 8.104/TH = 6.104/TE 8.104TE= 6.104TH TE TH energia interna não constante.

R- A energia interna ∆U é constante apenas em I.

B) Em I não ocorre variação de energia interna.

Em II e III houve aumento de temperatura e, consequentemente aumento de energia interna.

Em IV houve diminuição de temperatura e, consequentemente diminuição de energia interna.

O aumento de enet=rgia interna ocorreu apenas em II e III e, como a energia interna é diretamente proporcional à temperatura absoluta, de A:

II. TG = 2TF = 2

III. TH = 2TG = 2

C) Veja informação abaixo:

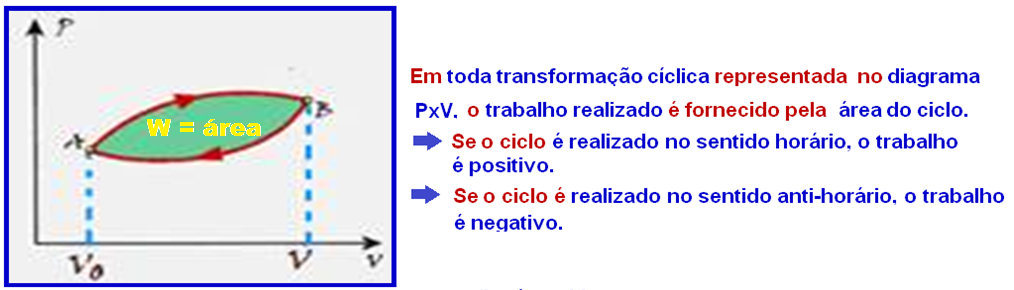
No caso doe exercício vamos calcular a área do ciclo lembrando que nos trechos FG e HE o trabalho é nulo (transformação isovlumétrica).

Cálculo do trabalho W no trecho GH onde ele fornecido pela área do trapézio e é positivo (sentido horário):

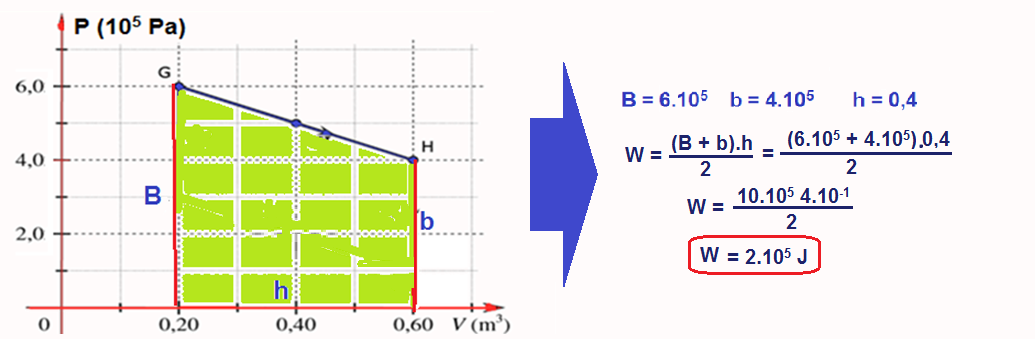
Cálculo do trabalho W no trecho EF onde ele éfornecido pela área do trapézio e é negativo (sentido anti-horário):

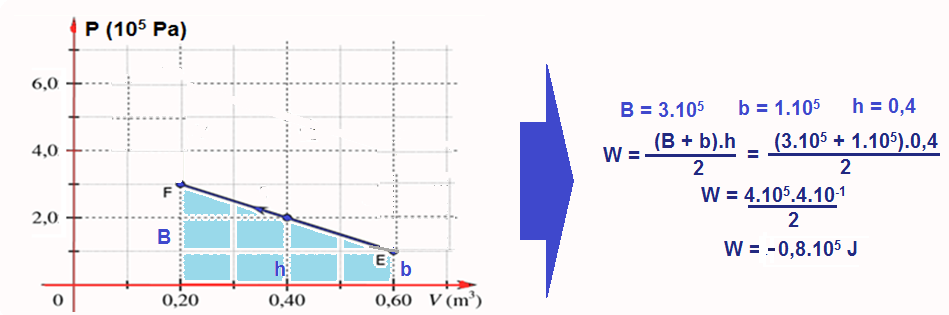
W = 2.105 – 0,8.105 = 1,2.105 J

Po = Po = = 0,02.105 Po = 2.103 W como são 50 ciclos Po = 50.2.103

Po = 100 kW.

27-

A seguir, breve resumo teórico:

Transformação isobárica

Ocorre à pressão constante. A variação de temperatura (ΔT) provoca umavariação de energia interna (ΔU) do sistema e a variação de volume (ΔV) produz trabalho.

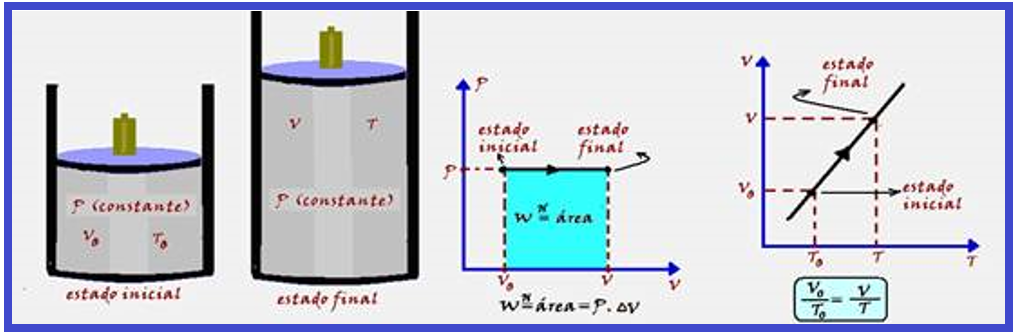
Parte do calor (Q) recebido pelo sistema é armazenada sob forma de energia interna e parte é transformada em trabalho, de modo que ΔU = Q – W.

No caso do exercício, são fornecidos:

P = constante = 1 atm = 1.10⁵ N/m² (Pa)

Volume inicial V_o = 1000 cm³ = 10³ cm³ = 10³.(10^-6 m³) Vo = 10^-3m³

Volume final que foi aumentado 300% V =( ).10^-3 V = 3.10^-3 m³

Cálculo do trabalho mecânico, em joules, realizado pelo gás durante essa transformação W = P.∆V = 10⁵.(3.10^-3 – 1.10^-3) W = 10⁵.2.10^-3 W = 2.10² J

Energia interna de um gás perfeito

A energia interna (U) de um gás perfeito monoatômico corresponde à soma das energias cinéticas médias (Ec) de todas as suas moléculas e, pela lei de Joule é fornecida por:

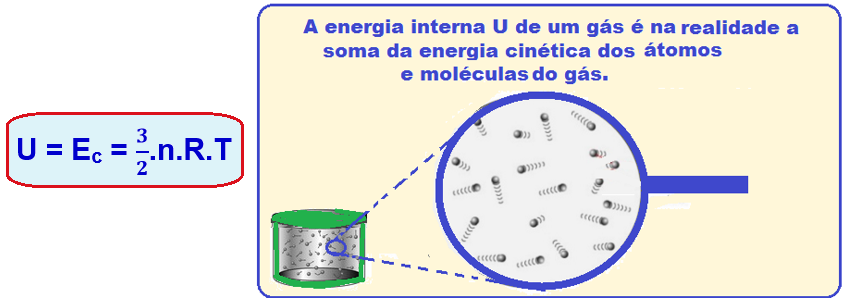
A energia interna de certa massa de um gás perfeito é função exclusiva da temperatura desse gás

Se U = (3/2).n.R.T e PV = n.R.T U = (3/2).PV ∆U = (3/2).P.∆V = ( . 10⁵.2.10^-3 ∆U = 3.10² J.

R- D

28-

Equação de Clapeyron ou Equação de um gás ideal

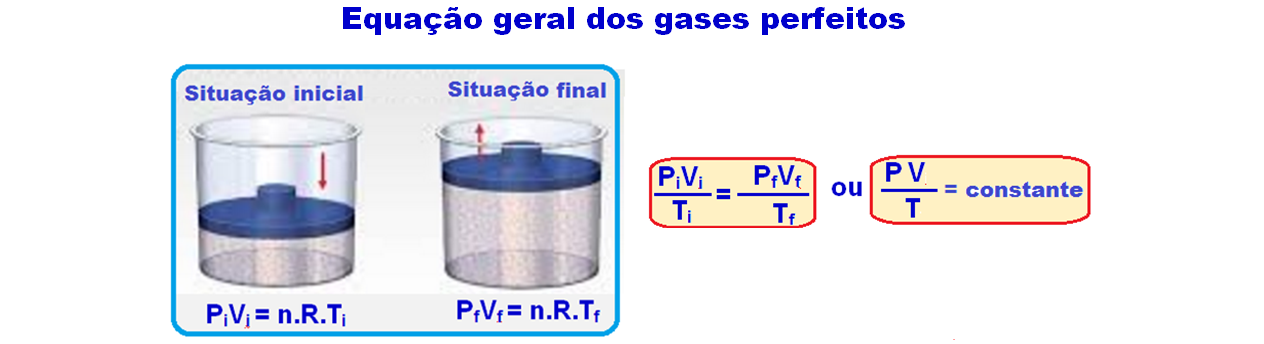
Pelo gráfico:

Ponto A PA = 2.10⁵ N/m² VA = 2.10^-3 m³ TA

Ponto B PB = 5.10⁵ N/m² VB = 6.10^-3 m³ TB

Primeiro Princípio da Termodinâmica ou Princípio da Conservação da energia

O Primeiro Princípio da Termodinâmica (Princípio da Conservação da Energia) afirma que: “A energia não pode ser criada nem destruída, mas apenas transformada”

Exemplo numérico:

Suponha que um sistema isolado receba Q = 300 J de calor. Se, por exemplo, ∆U = 50 J dessa energia forem absorvidos pelo sistema aumentando sua energia interna de 50 J, então a parte restante, W = 250 J, será fornecida ao ambiente sob forma de trabalho.

Então, Q = W + ∆U ou ∆U = Q – W.

Como nas transformações ACDEB e AFB os estados inicial (A, de temperatura TA)) e final (B, de temperatura TB) coincidem, a variação de energia interna ∆U será a mesma nas duas transformações

∆UACDEB = ∆UAFB.

∆UACDEB = Q1 – W1 e ∆UAFB = Q2 – W2 Q1 – Q2 = W1 – W2.

Mas, em toda transformação representada no diagrama PxV, o trabalho realizado é numericamente igual à área.

Cálculo do W1 no trecho ACDEB:

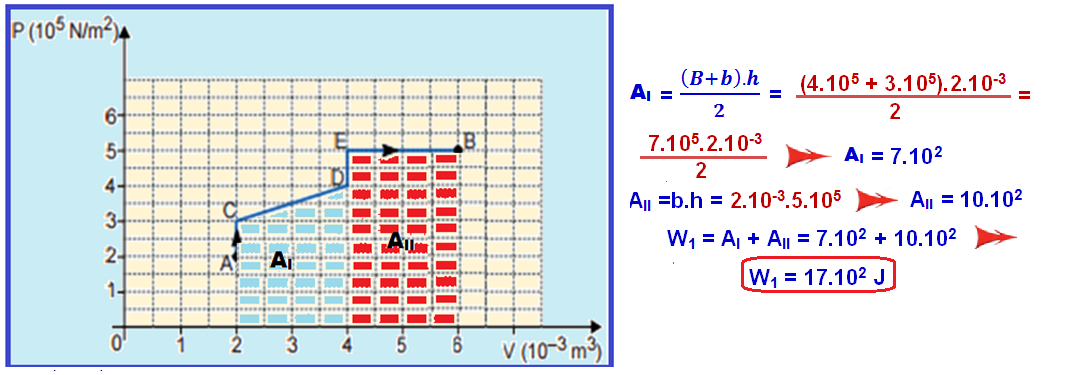
Cálculo do W2 no trecho AFB:

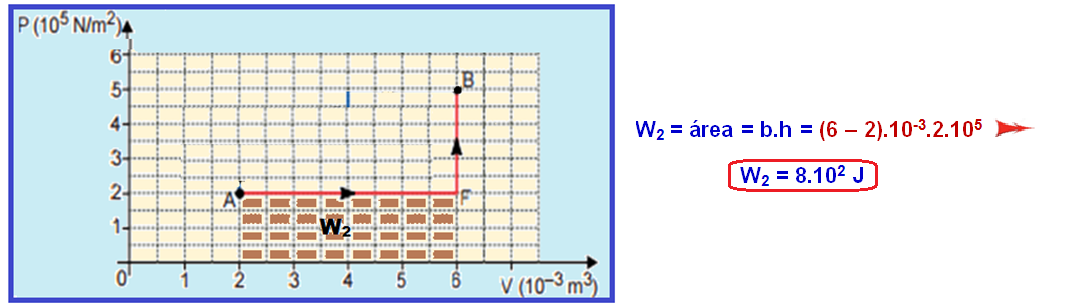
Q1 – Q2 = W1 – W2 = 17.10² – 8.10² Q1 – Q2 = 9.10² J

29–

I. O trabalho total realizado no ciclo ABCA é nulo.

I. Falsa — Em toda transformação cíclica representada no diagrama PxV, o trabalho realizado é

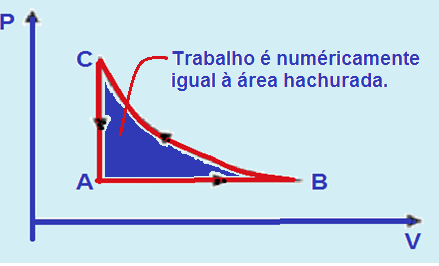
fornecido pela área do ciclo.

Se o ciclo é realizado no sentido horário, o trabalho é positivo.

Se o ciclo é realizado no sentido anti-horário, o trabalho é negativo.

II. A energia interna do gás no estado C é maior que no estado A.

II. Correto — no trecho CA a transformação é isovolumétrica onde o volume V1 é constante.

Observe nas figuras abaixo que quanto maior a temperatura maior é o movimento vibratório das

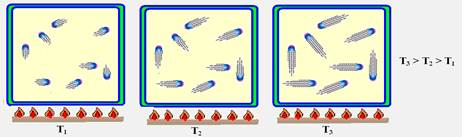
moléculas do gás e consequentemente maior a energia cinética (Ec) de suas moléculas, o que implica num aumento da energia interna (U) do gás.

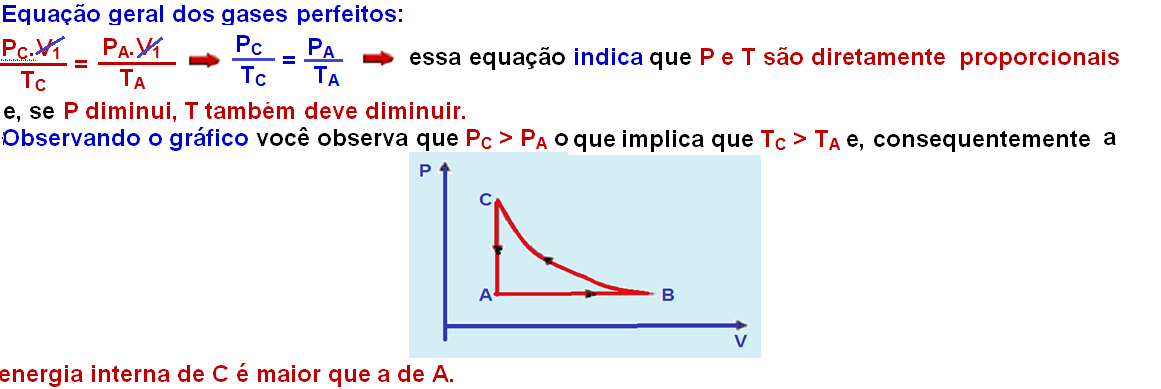
III. Durante a transformação , o gás recebe calor e realiza trabalho.

Observe no gráfico que no trecho AB o volume está aumentando (VB > VA) e o trabalho realizado é positivo, pois, numa isobárica W = P.(VB – VA) e, sendo P positiva e constante e (VB – VA) > 0, o trabalho será WAB > 0.

A transformação BC é isotérmica (mesma temperatura, TB = TC) e, como vimos em I, TB=TC > TA o que implica que UB > UA fazendo com que avariação de energia interna ∆U = UB – UA seja positiva (∆UAB > 0.

Pela segunda lei da termodinâmica ∆U = Q – W QAB =∆UAB + WAB como ∆UAB e WAB são positivos, QAB > 0 e o gás recebe calor e realiza trabalho.

R- E

30-

Rendimento real η do motor

A potência total absorvida por esse motor em ∆t = 1 s vale Pt = = =

Pt = 3700 J/s Pt = 3700 W.

Potência útil do motor Pu = 2,5×740 Pu = 1850 W.

Rendimento do motor ηm =Pu/Pt = ηm = 0,5 (50%)

Rendimento de um motor de Carnot

Temperatura Tf da fonte fria Tf =927 +273 = 1200 K.

Temperatura TQ da fonte quente = = = 403 – 160 = 9C C = 27 oC TQ = 27+273 = 300 K.

O rendimento ηC de um motor de Carnot operando entre as temperaturas acima é fornecido pela expressão ηC = 1 – TQ/Tf = 1 – = 1 – 0,25 ηC = 0,75 (75%)

Razão pedida ηC/ηm = ηC/ηm = 1,5

R- C

31-

T temperatura da fonte quente T = 1 160,6 ^oF = = = 9K – 2457 = 5643 K = T = 900 K

A temperatura da fonte fria é a da fonte quente menos 270oC = 270 + 273= 543 K T1 = 900 – 543 T1 = 357 K.

Rendimento da máquina térmica = 1 – T1/T = 1 – = 1 – 0,4 = 0,6 = 60%

R – ?

32-

São dados:

Q1 quantidade de calor recebido da fonte quente num ciclo Q1 = 4,0.103 J

Q2 quantidade de calor rejeitado para a fonte fria num ciclo Q2 = 2,8.103 J

b) Cálculo do trabalho realizado em cada ciclo = Q1 – Q2 = 4,0.103 – 2,8.103 = 1,2.103 J

Como são 3000 ciclos o trabalho total será total = 1,2.103×3000 total = 3,6.106 J.

33-

η = 1 – = 1 – = 0,5 η = 50 %.

T1 = 27 + 273 = 300 K η = 1 – 0,5 = 1 – – 0,5 = – T = 600 K.

R- D

Voltar para os exercícios