Vestibulares Recentes – Resolução Comentada – Eletrostática – 2018/2019

01-

Aqui, a única alternativa incorreta é alternativa (C), pois a carga elétrica é transferida exclusivamente pelo movimento dos elétrons, deixando os prótons fixos. A carga positiva acaba sendo então dada pela ausência de elétrons. Logo, a (C) deve ser a alternativa marcada.

02-

Eletrização por contato

Pode ocorrer entre dois condutores (cargas elétricas se distribuem em suas superfície externas) ou entre um condutor e um isolante (no isolante as cargas elétricas ficam somente no local do contato).

Considere um condutor A eletrizado com carga positiva (QA = + Q) e outro condutor B,
eletricamente neutro (QB = 0) presos a suportes isolantes (para que não descarreguem),inicialmente separados.

Quando são colocados em contato, os dois se comportam como se fossem um único corpo e haverá uma distribuição de cargas nas superfícies de A e de B.

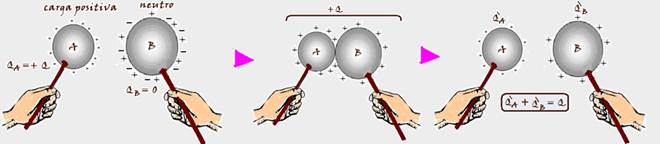
Após essa distribuição de cargas são separados e A ficará com carga QA’ e B com carga QB’, tal que QA’ + QB’ = + Q (princípio da conservação das cargas elétricas).

Observe que, se os condutores forem idênticos e com as mesmas dimensões, você teria QA’ = QB’= Q’ Q’ + Q’ = + Q Q’=Q/2

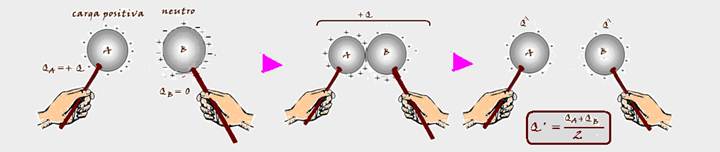
Se os dois corpos forem idênticos e estiverem inicialmente eletrizados com cargas QA e QB, após o contato eles terão cargas idênticas Q’ tal que Q’= (QA + QB)/2.

No caso do exercício:

R- A

03-

Corpos eletrizados

Q = n.e 1 = n.1,6.10-19 n = 1/1,6.10-19 = 0,625.1019 = 6,25.1018 elétrons.

R- C

04-

Eletrização por contato

Se os dois corpos forem idênticos e estiverem inicialmente eletrizados com cargas QA e QB, após o contato eles terão cargas idênticas Q’ tal que Q’= (QA + QB)/2.

Esfera de carga Q em contato com a primeira, neutra Q’ =(Q + 0)/2 Q’ = Q/2.

Esfera de carga Q’ em contato com a segunda, neutra Q’’ =(Q/2 + 0)/2 Q’’ = Q/4.

Esfera de carga Q’’ em contato com a terceira, neutra Q’’’ =(Q/4 + 0)/2 Q’’’ = Q/8.

Esfera de carga Q’’’ em contato com a quarta, neutra Q’’’’ =(Q/8 + 0)/2 Q’’’’ = Q/16.

R- B

05-

Se você não domina a teoria, ela é extensa e está a seguir:

Eletrização por atrito

Para que ocorra eletrização por atrito os corpos atritados devem ser de materiais diferentes e a distribuição de cargas obedece à série triboelétrica abaixo (fornecida).

Atritando quaisquer materiais dessa série, o que estiver à esquerda ficará com carga positiva e o da direita, negativa.

Eletrização por contato

Pode ocorrer entre dois condutores (cargas elétricas se distribuem em suas superfícies externas) ou entre um condutor e um isolante (no isolante as cargas elétricas ficam somente no local do contato).

separados.

Quando são colocados em contato, os dois se comportam como se fossem um único corpo e haverá uma distribuição de cargas nas superfícies de A e de B.

Após essa distribuição de cargas são separados e A ficará com carga QA’ e B com carga QB’, tal que QA’ + QB’ = + Q (princípio da conservação das cargas elétricas).

Observe que, se os condutores forem idênticos e com as mesmas dimensões, você teria QA’ = QB’= Q’ Q’ + Q’ = + Q Q’= Q/2

Se os dois corpos forem idênticos e estiverem inicialmente eletrizados com cargas QA e QB, após o contato eles terão cargas idênticas Q’ tal que Q’= (QA + QB)/2.

Exemplos:

Em todos os casos a seguir as esferas são idênticas, e depois de colocadas em contato são separadas e cada uma delas ficará com carga Q’:

a) QA = 0 e QB= – 8μC Q’ = (QA + QB)/2 = (0 – 8μ)/2 Q’= – 4μC (carga de cada uma após o contato)

b) QA= 2C e QB= – 6C Q’ = (QA + QB)/2 = (2 – 6)/2 Q’ = -2C (carga de cada uma após o contato)

c) QA = 6μC, QB = -8 μC e QC= 12 μC Q’ = (QA + QB + QC)/3=(6 μ – 8 μ + 12 μ)/3 Q’= (10/3) μC.

Eletrização por indução

Induzir eletricamente significa provocar uma separação de cargas, sem que haja contato. Observe dois processos:

Primeiro processo Considere duas esferas condutoras, inicialmente descarregadas (neutras) e encostadas uma na outra (figura 1). Aproxima-se, sem encostar, uma terceira esfera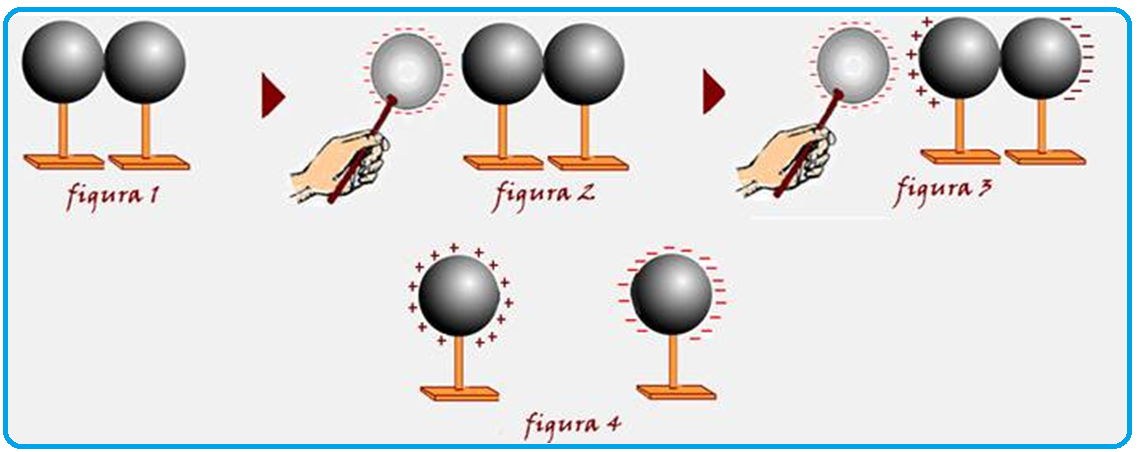

condutora eletrizada.

A esfera eletrizada provoca uma indução elétrica (movimentação de cargas) nas outras duas até que elas apresentem a distribuição indicada na figura 3.

Em seguida, sem tirar do lugar a esfera eletrizada, afasta-se um pouco uma esfera da outra. Finalmente, sem mexer mais nas esferas, remove-se a esfera eletrizada, levando-a para muito longe das esferas.

Nessa situação final, as cargas se espalham ficando na superfície externa de cada carga, ficando eletrizadas conforme a figura 4.

Segundo processo Aproxima-se um condutor eletrizado, por exemplo, negativamente (indutor) de um condutor neutro que se deseja eletrizar (induzido), sem encostar, mas bem próximos (figura 1).

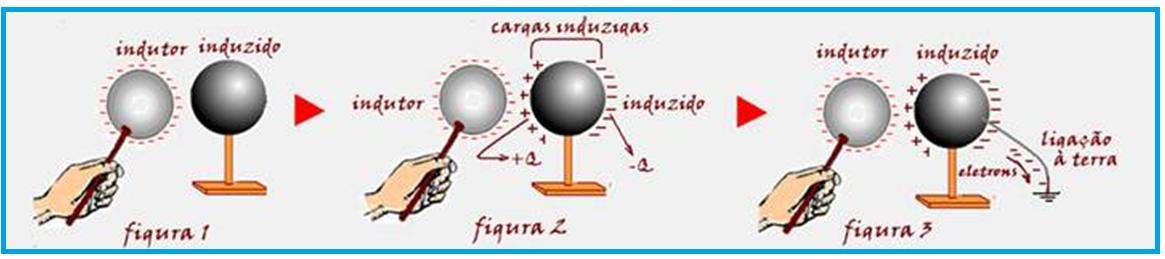
Os elétrons livres do indutor serão repelidos, ficando o lado direito do induzido com excesso de elétrons e o lado esquerdo com falta de elétrons, fenômeno que recebe o nome de indução elétrica (figura 2).

As cargas elétricas que se concentram nas duas extremidades opostas (denominadas cargas induzidas) são de mesmo módulo, mas de sinais opostos e, por esse motivo o induzido continua neutro.

Em seguida, ainda na presença do indutor você liga o induzido à terra (fio terra ou com seu dedo) e observa que elétrons se deslocam do induzido para a terra (figura 3).

Se o indutor tivesse cargas positivas, ao final de todo o processo o induzido ficaria eletrizado com cargas negativas.

R- A

06-

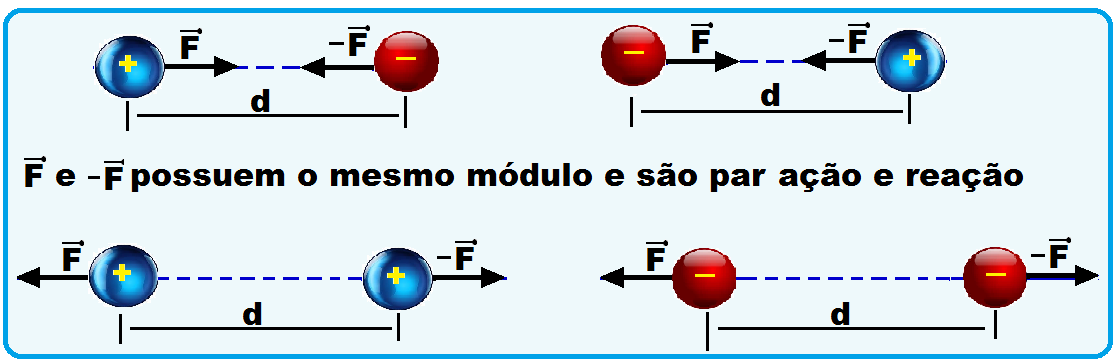
s forças elétricas trocadas entre A e B são de repulsão (qA e qB se repelem “mesmo sinal”) e possuem a mesma intensidade (módulo) pelo princípio da ação e reação FA = FB.

Como as setas representam as acelerações, a intensidade (módulo) de B é maior que a de A aB > aA.

Segunda lei de Newton FA = mA.aA e FB = mB.aB FA = FB mA.aA = mB.aB como aB > aA, mB deve ser menor que mA mB < mA.

R- D

07-

Campo Elétrico Uniforme

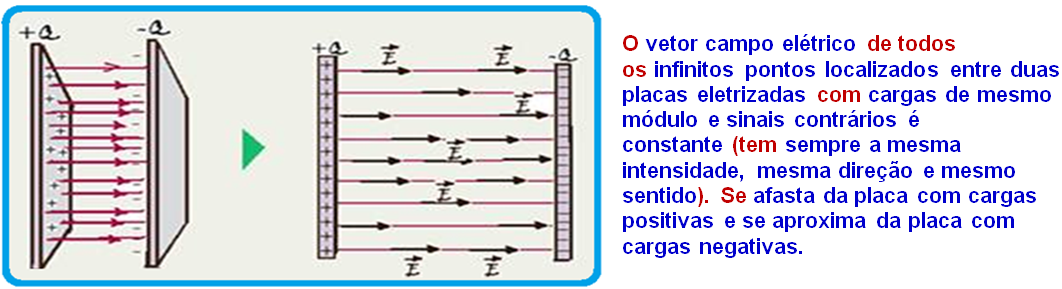
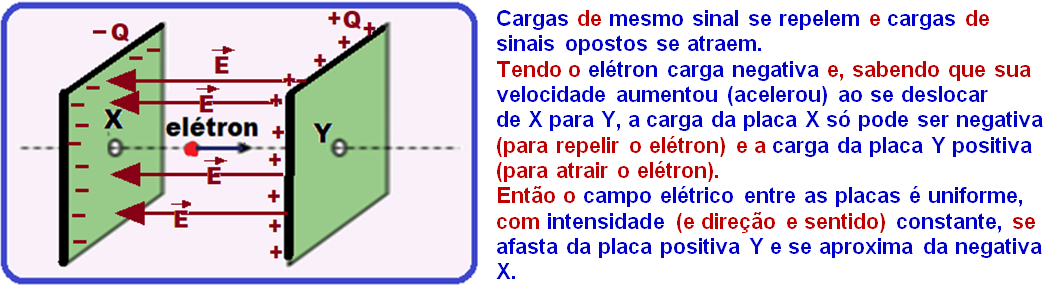
R – C

08-

Representação esquemática das linhas de campo ou linhas de força de um campo elétrico

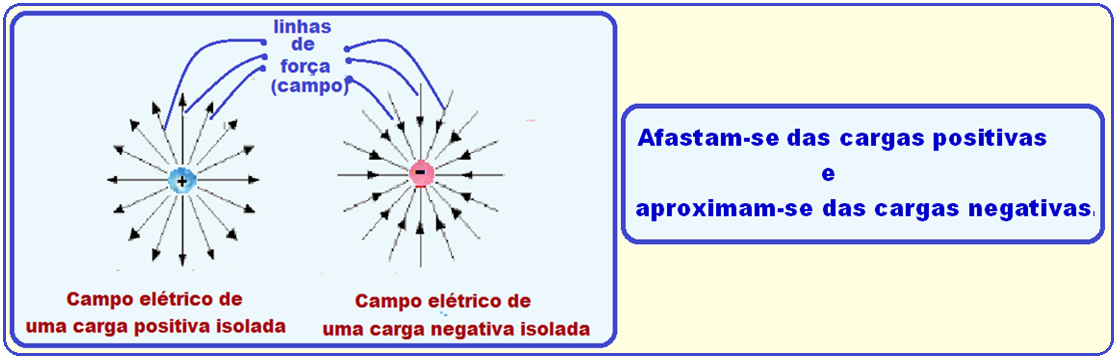
R- D

09-

Campo elétrico

Como a carga q é negativa e o campo elétrico tem direção vertical e sentido para baixo então a força elétrica sobre q t terá direção vertical e sentido para cima.

Na figura abaixo estão a força elétrica e o peso que agem sobre a carga q.

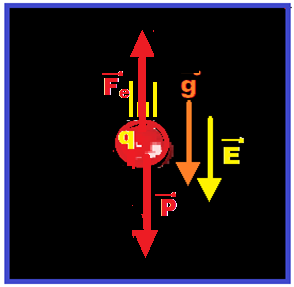
R- (02 + 04 + 08) = 14

10-

Se o campo elétrico é uniforme, temos que:

Vamos retomar a imagem do exercício:

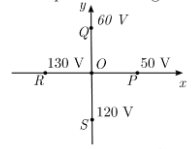
Vamos analisar a diferença de potencial U na dimensão X e Y, para isso vamos isolar o E na equação de cima:

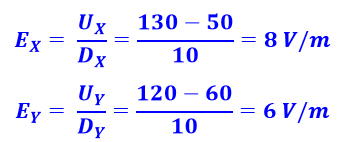
Agora que sabemos os campos em X e Y precisamos achar o seu resultante, como eles são ortogonais (estão a 90° um do outro), podemos usar Pitágoras:

Alternativa correta é a D.

11-

Como o enunciado pede o campo elétrico fora da casca esférica, podemos usar o princípio da superposição, que diz que o campo E1 fora da casca esférica será igual a soma de um campo E4a gerado por uma esfera de raio 4a carregada positivamente e de outro campo Ea gerado por uma outra esfera de raio a carregada negativamente, ambas posicionadas no mesmo centro:

No qual k0 é a constante elétrica no vácuo. Caso o campo dê positivo, ele é radial para fora, enquanto que se for negativo, é radial para dentro. Essa mesma fórmula pode ser usada para as esferas de carga Q e de qualquer raio R, porém foi dada a densidade volumétrica de carga ρ ao em vez da carga elétrica Q, devemos então fazer a conversão utilizando a definição de densidade de carga, que é a carga dividida pelo volume:

O campo total E será então a soma de todos os campos calculados:

12-

a) A corrente média é definida como a variação de carga sobre um intervalo de tempo. A variação da carga elétrica total é o número de elétrons que fluiu de uma esfera até a outra multiplicada pela carga elétrica fundamental do elétron:

Substituindo a última equação na primeira, e colocando os valores dados no enunciado, chegamos em:

b) O campo elétrico é dado pela relação:

Em que k é a constante eletrostática do meio (neste caso é a do ar), Q é o valor da carga geradora e d é a distância da carga geradora ao ponto em que queremos conhecer o valor do campo.

Repare que teremos dois campos atuando no ponto M relacionados às esferas 1 e 2. Utilizando a fórmula do campo elétrico para as esferas teremos:

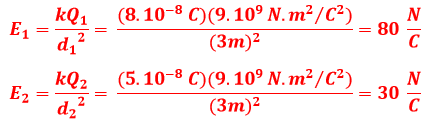
Para encontrar o campo elétrico total no ponto M, devemos observar o vetor dos campos elétricos das esferas individualmente, respeitando a seguinte constatação:

Objetos com carga positiva possuem suas linhas de campo apontando para fora.
Objetos com carga negativa possuem suas linhas de campo apontando para dentro.

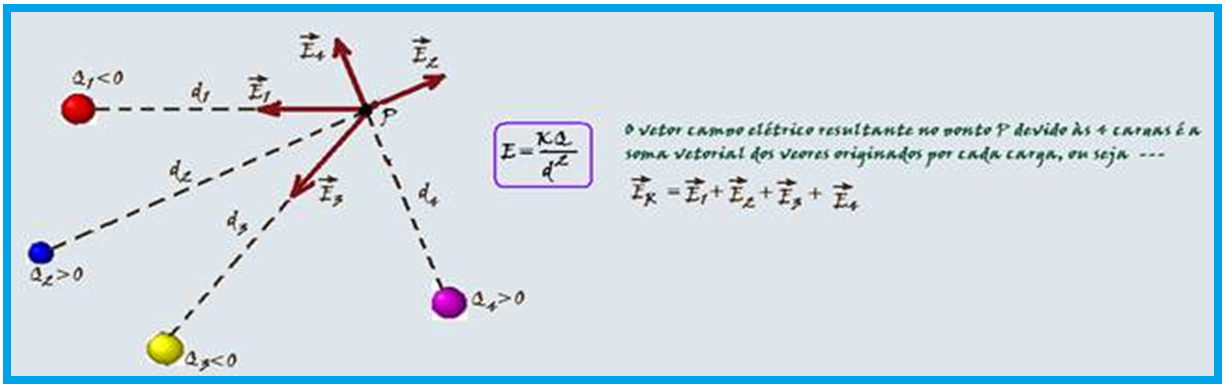
Logo abaixo há uma ilustração de como as linhas de campo se comportam para objetos redondos carregados.

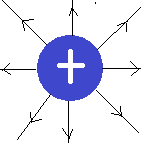
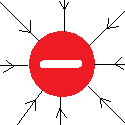
Aplicando este conceito na figura, temos:

Como os campos estão opostos um ao outro no ponto M, o módulo do campo total nesse ponto será dado pela diferença entre os dois, tal que:

13-

14-

Como, pelo enunciado o elétron se desloca de A para B, então a placa A é negativa (menor potencial), pois deve repelir o elétron (carga negativa) e a placa B é positiva (maior potencial) devendo atrair o elétron.

I. Correta Considerando a força elétrica como a força resultante sobre o elétron (única força que age sobre ele) e lembrando que o campo elétrico entre as placas é uniforme, vamos calcular o trabalho da força elétrica entre A e B (WAB), em função da diferença de potencial entre A e B sabendo que o elétron possui carga negativa e que VA < VB:

WBA = q.(VA – VB) = (-1,6.10-19).(- 2,0.104) = 3,2.10-15 J. (Observe que esse trabalho independe da trajetória dependendo apenas de q e de (VA – VB) que são os mesmos para as duas trajetórias)

Esse trabalho também é o mesmo quando calculado pela variação da energia cinética (Teorema da energia cinética) WAB = EcB – EcA 3,2.10-15 = EcB – mVA2/2 = EcB – m.02/2 = EcB – 0 EcB = 3,2.10-15 J.(energia cinética com que o elétron atinge a placa B).

II. Correta Como já vimos em I.

III. Falsa Veja I e II.

R- D

15-

Essa descarga entre a nuvem (cargas negativas) e o solo (cargas positivas) através do ar (dielétrico) que, devido à elevada ddp U entre as nuvens e o solo se transforma em condutor, tem o mesmo comportamento elétrico que o de um capacitor de capacidade C = Q/U.

Supondo essa capacidade constante, o gráfico UxQ está representado abaixo:

Mas observe que não temos a diferença de potencial. Então vamos encontrá-la. O enunciado informa que temos um campo elétrico uniforme:

Substituindo U = E.d em Ep = Q.U/d Ep =

Q carga elétrica transportada Q = 2.102 C.

E intensidade do campo elétrico entre a base da nuvem e o solo E = 5.106 V/m.

d distância entre a base da nuvem e o solo d = 500 m.

Substituindo esses valores em Ep = Ep = = 2500.108 Ep = J.

R- C