Resolução Eletrostática – 2014 – 2013
Resolução Comentada – 2014- 2013
ELETROSTÁTICA
01-
Lei de Coulomb:
Cargas elétricas de mesmo sinal se repelem e de sinais opostos se atraem — analise atentamente a figura abaixo:
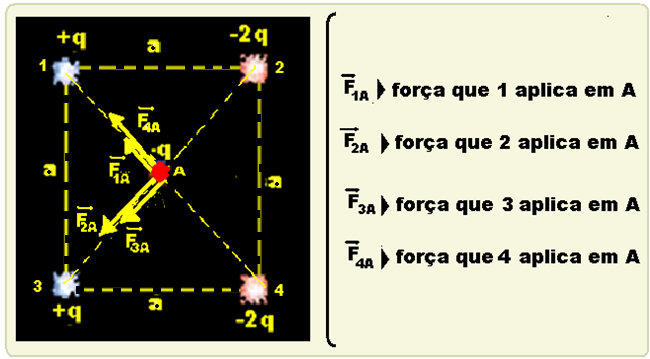
Observe que pela lei de Coulomb F=KQq/d2 que — F4A = F2A e que F1A = F3A — adicionando vetorialmente essas forças você obtém a força resultante 
pedida, cuja direção e sentido
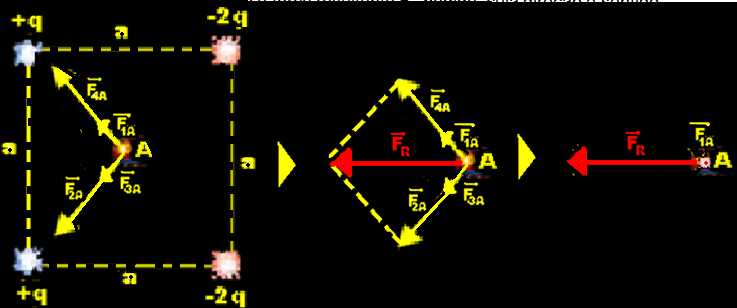
estão indicados na figura — R – B
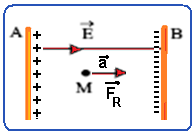
02- Por convenção, as linhas de força do campo elétrico e, consequentemente, o próprio campo elétrico 
se afastam das cargas positivas e se aproximam das negativas — assim, a placa A está eletrizada com cargas positivas e a B com cargas negativas
Quando a partícula com carga positiva q é abandonada em M ela será repelida pela placa A, positiva e atraída pela placa B, negativa, se deslocando para a direita até atingir a placa B.
Como são desprezados os efeitos gravitacionais (força peso) e existe o vácuo entre as placas (não existe atrito) a força resultante (FR=m.a) sobre a carga q será a força elétrica de intensidade FR=q.E, tal que:
Então a partícula de carga positiva q é acelerada a partir de M (de onde sai do repouso Vo=0) e, após percorres d/2 atinge a placa B com velocidade V, fornecida pela equação de Torricelli:
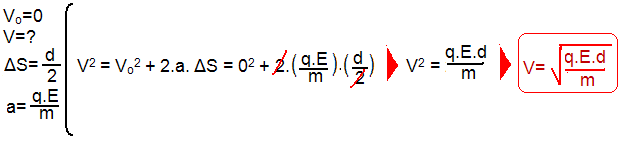
R- B
03- Sendo n as esferas, quando separadas em agrupamentos com quantidades iguais de esferas, cada agrupamentos A, B e C terá n/3 esferas idênticas conforme a figura:
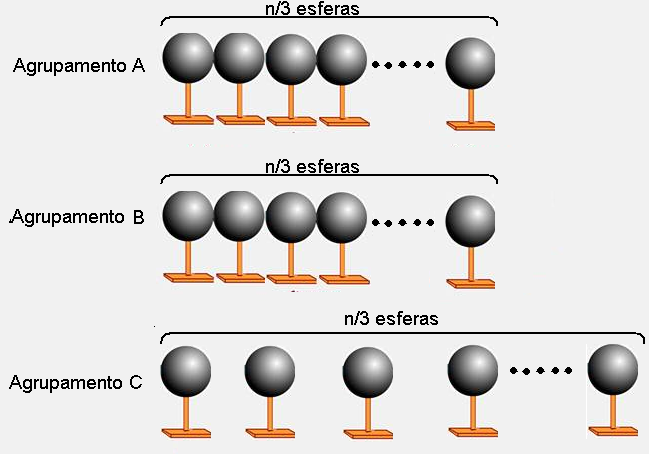
Quando você coloca a esfera P eletrizada com carga Q em contato com as n/3 esferas idênticas e neutras,
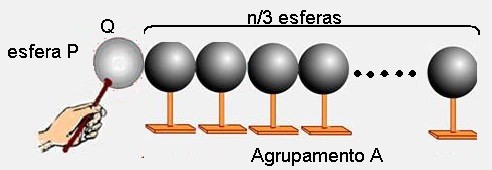
do agrupamento A, essa carga Q será igualmente distribuída entre as (1 + n/3) esferas e a nova carga Q’ da esfera P será:
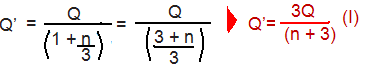
Agora você vai colocar essa nova carga Q’ da esfera P em contato com as (1 + n/3) esferas idênticas e
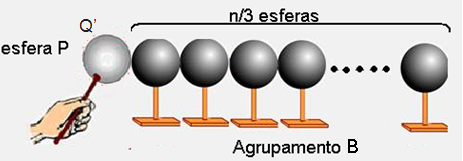
neutras do agrupamento B e a nova carga Q’’ da esfera P será:
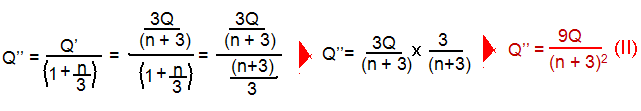
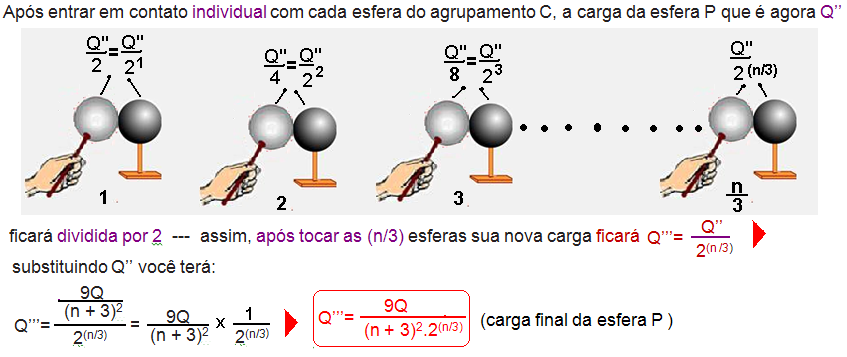
R- B
04- Fq1Q=kq1.Q/d2=9,109.4.10-6.5.10-6/(5.10-1)2=180.10-3/25.10-2 — Fq1Q = Fq2Q = 7,2.10-1 = 0,72N.
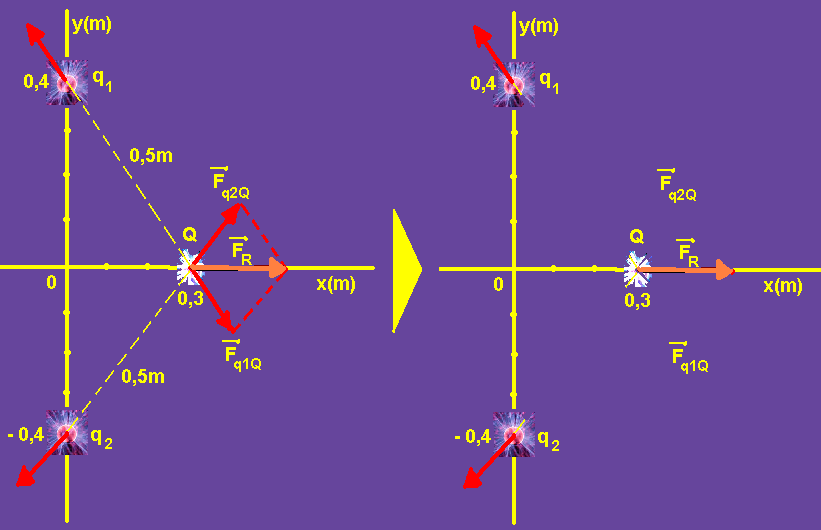
Observe na figura acima que a força resultante é a soma vetorial das duas força achadas — FR2 = 0,722 + 0,722=2.0,722 — FR=0,72.√2=0,72.1,4 — FR=1,008×10=10N
05- Condutores: Aproxima-se um condutor eletrizado, por exemplo, negativamente de um condutor neutro, sem
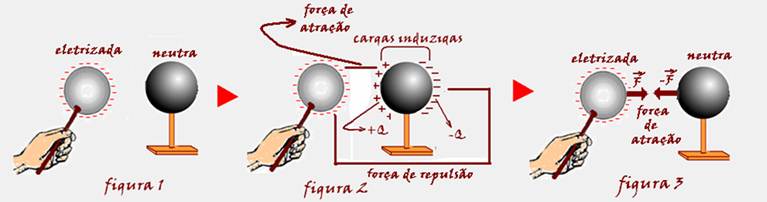
encostar, mas bem próximos (figura 1).Os elétrons livres do indutor serão repelidos, ficando o lado direito do induzido com excesso de elétrons e o lado esquerdo com falta de elétrons, fenômeno que recebe o nome de indução elétrica (figura 2). Observe na figura 2 que a força de atração entre as cargas negativas e positivas é maior que a força de repulsão entre as cargas negativasporque a distância entre as cargas que se atraem é menor e, quanto menor a distânciaentre cargas de mesmo módulo, maior a força entre elas.
Isolantes: Polarização de cargas num isolante — nos isolantes a polarização acontece nas moléculas ou os átomos da superfície do corpo.
Polarização atômica
| Nos isolantes a polarização acontece nas moléculas ou os átomos da superfície do corpo.
Polarização atômica
Nos átomos, em torno do núcleo positivo, os elétrons se distribuem numa “nuvem eletrônica” com densidades variáveis; onde a densidade for maior, maior é a probabilidade de se encontrar os elétrons. Essa nuvem pode ser deformada, deslocando os centros de cargas positivas e negativas em dois pólos. Com as moléculas – combinação de átomos – também ocorre o fenômeno da polarização. |
R- B.
06- Os vetores em azul representam as forças trocadas entre cada esfera e observe que
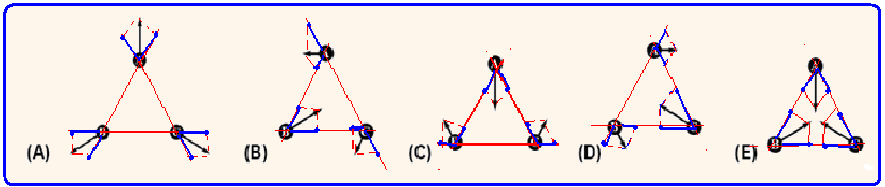a incompatível é a a alternativa E, pois se a força entre dois pares é de atração (sinais opostos), a força entre o outro par deverá ser de repulsão (mesmo sinal).
R- E
07- Os dois geradores se comportam como se fossem um só de ε=5V, eletrizando o capacitor C com essa ddp. de U=5V.
Energia no capacitor — W=Q.U/2 — 125.10-6 = Q.5/2 — Q=50.10-6C.
Capacitância do capacitor — C=Q/U=50.10-6/5 — C=10.10-6 F.
R- A
08- Se B tem carga negativa e repele A então A terá também carga negativa (cargas de mesmo sinal se repelem).
Se, quando o objeto metálico é aproximado de A que possui carga negativa é atraído, ou ele possui carga positiva ou está neutro e é atraído por indução.
R- B
09- I. Falsa — o campo é mais intenso onde ocorre maior concentração de linhas de campo elétrico, no caso, na região B.
II. Falsa — veja III.
III. Correta — veja na figura abaixo que quem origina esse campo é uma carga negativa e por isso
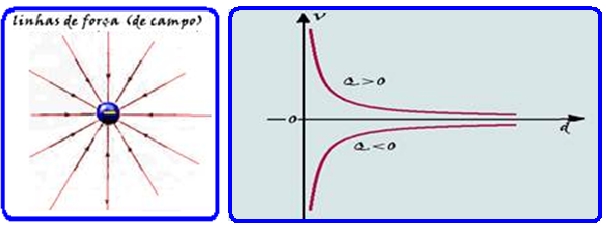
o potencial elétrico é maior em A, conforme você pode observar na parte inferior do gráfico acima que fornece os valores algébricos do potencial de uma carga negativa.
R- C
10- Sendo a carga elétrica q negativa e o campo elétrico vertical e para baixo, a força elétrica sobre a carga q terá direção vertical e para cima e intensidade — Fe=q.E=q.50 — Fe=50q.
Peso do balão — P=mg=10-3.10 — P=10-2N.
Como ele flutua a resultante das forças que agem sobre ele é nula e Fe=P — 50q = 10-2 — q=
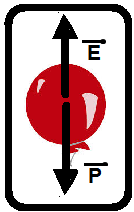
10-2/50=0,02.10-2=2.10-2.10-2 — q=200.10-6=200 μC.
R- A
Carga elétrica e processos de eletrização
70- 01. Falsa — ficará com carga positiva, mas é porque cederá elétrons ao teflon.
02. Correta — Na figura abaixo você dispõe de uma placa de vidro e de um pano de lã presos em suportes isolantes
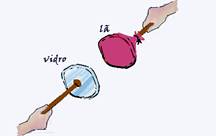
para não descarregar), ambos inicialmente neutros. Em seguida, são atritados (esfregados) e depois separados e isolados sem influência elétrica externa de outros corpos. Nessas condições, a quantidade de cargas elétricas (elétrons livres) que um cede é a mesma que o outro recebe, ou seja, o vidro cederá elétrons e adquirirá carga positiva +Q e a lã receberá elétrons e ficará com carga de mesmo módulo, mas negativa –Q.
04. Correta — veja (02).
08. Correta — quanto mais afastados os elementos atritados estiverem na série triboelétrica, maior será a facilidade de transferência de elétrons maior quantidade de eletricidade estática adquirida.
16. Falsa — os dois bastões de vidro quando atritados com pele de gato ficam com cargas positivas e, quando aproximados irão se repelir, pois possuem cargas elétricas de mesmo sinal.
32. Falsa — só haverá transferência de elétrons se os materiais atritados forem diferentes.
R- (02 + 04 + 08)=14.
71- Sendo as esferas idênticas, após colocadas em contato e depois separas ambas ficarão com cargas elétricas de mesmo sinal e de valor Q=(Q1 + Q2)/2 — A com B — Q’=(+ 3e – 5e)/2 — Q’A=Q’B= – 1e — A com C — Q’’=(-1e + 3e)/2 — QA’’=QB’’= + 1e — R- C.
72- Leia a teoria a seguir:
Aproxima-se um condutor eletrizado, por exemplo, negativamente de um condutor neutro, sem
encostar, mas bem próximos (figura 1).Os elétrons livres do indutor serão repelidos, ficando o lado direito do induzido com excesso de elétrons e o lado esquerdo com falta de elétrons, fenômeno que recebe o nome de indução elétrica (figura 2) — observe na figura 2 que a força de atração entre as cargas negativas e positivas é maior que a força de repulsão entre as cargas negativas porque a distância entre as cargas que se atraem é menor e, quanto menor a distância entre cargas de mesmo módulo, maior a força entre elas — o corpo neutro continua neutro (mesmo número de prótons e de elétrons) — portanto, um corpo eletrizado pode atrair um corpo neutro, figura 3.
O mesmo ocorre se o bastão estiver eletrizado com carga positiva, só que agora você terá, na esfera neutra, cargas negativas do lado esquerdo e positivas do lado direito — R- E.
Força elétrica – Lei de Coulomb
44- São dados esfera superior, positiva de módulo — q1=0,001C=10-3C — esfera inferior negativa de módulo q2=2,5.
10-9C — m2=9g=9.10-3kg — peso de m2 — P2=m2.g=9.10-3.10 — P2=9.10-2N — sendo as cargas de sinais opostos a força elétrica de intensidade Fe entre elas é de atração e, estando as partículas em equilíbrio a força resultante
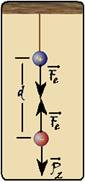
sobre a partícula 2 é nula e, sobre ela — Fe=P2 — kq1.q2/d2 = 9.10-2 — 9.109.10-3.2,5.10-9d2 = 9.10-2 — d2=22,5. 10-3/9.10-2 — d2=2,5.10-1 — d=√0,25 — d=0,5m — R- B.
45- Trata-se de um movimento circular uniforme onde, em cada ponto a força elétrica sobre (-q) de direção radial e para o centro da circunferência tem intensidade Fe=kQq/R2 — essa força é igual à força resultante centrípeta sobre (-
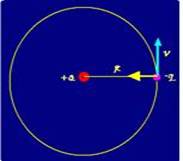
q) de intensidade Fc=mV2/R — Fe = Fc — kQq/R2 = mV2/R — kQq/R = mV2 (I) — por outro lado, como Q está em repouso,a energia total do sistema é a cinética de (-q), Ec=mV2/2 mais a energia potencial elétrica do sistema fornecida por Ep=kQ(-q)/R2 — Et=mV2/2 – kQq/R2(II) — (I) em (II) — Et=mV2/2 – mV2 — Et = – mV2/2 —
R- D.
46- Carga elétrica que foi transferida de um para outro — regra de três — 1e – 1,6.10-19C — 5.103e – Q — Q=5.1013×1,6.10-19 — Q=8.10-6C — um deles, que recebeu elétrons, ficou com excesso de elétrons (carga negativa de Q= – 8.10-6C0 e o outro, que cedeu elétrons, ficou com carga positiva de Q=8.10-6C — como os dois corpos ficaram com cargas de sinais opostos a força entre eles será de atração — a intensidade dessa força é fornecida por F=K.Q.Q/d2, onde as cargas Q estão em módulo — F=9.109.8.10-6.8.10-6/(10-2)2=576.10-3/10-4 — F=5760N=5,76kN — R- E.
47- a) A velocidade dos neutrinos é a mesma que a da luz no vácuo(e aproximadamente, no ar) — V=3.108m/s — distância do Sol à Terra — ∆S=1,5.1011m — V=∆S/∆t — 3.108=1,5.1011/∆t — ∆t=1,5.1011/3.108=0,5.103 — ∆t=500s=8min2s.
b) Observe a seqüência das figuras abaixo, onde a tração 
foi decomposta em suas componentes
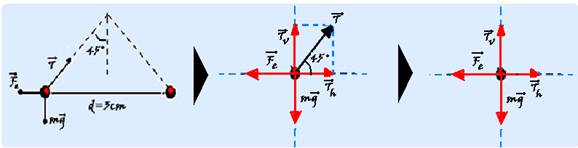
horizontal 
e vertical 
— Th=Tcos45o=(√2/2).T — Tv=Tsen45o=(√2/2).T — equilíbrio na vertical — Tv=mg — (√2/2).T= mg — T=√2.mg — equilíbrio na horizontal — Fe=Th — Fe=(√2/2).T=(√2/2).√2.mg — Fe=mg=0,004.10-3.10 —
m=4.10-5kg — Fe=kq2/d2 — 4.10-5 = 9.109.q2/(3.10-2)2 — q2 = 4.10-2.9.10-4/9.109 — q=√(4.10-18) — q=2.10-9C — (essas duas cargas são ambas positivas ou ambas negativas, pois as hastes se repelem).
Campo Elétrico
73- Dado — q2=2q1 — d2=(1 – q1) — E1=kq1/d12 — E2=k2q1/(1 – d1)2 — campo elétrico resultante nulo — E1 =
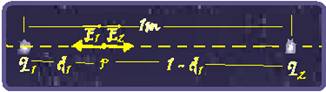
E2 — E1=kq1/d12 = k2q1/(1 – d1)2 — 1/d12 = 2/(1 – d1)2 — (1 – d1)2/d12=2 — {(1 – d1)/d1}2=2 — {(1 – d1)/d1}=√2 — (1 – d1)/d1=1,4 — 1,4d1 = 1 – d1 — d1=1/2,4 — d1=0,4m — R- B.
74- Cargas positivas criam, a certa distância d delas, campos de afastamento e negativas, campos de aproximação —
A intensidade desses campos é fornecida por E=kq/d2, onde q é o módulo da carga — para que o campo elétrico seja
nulo no ponto C, tendo as duas cargas mesmo sinal (positivo ou negativo), a condição é — E1=E2 — kq1/d2 = kq2/(3d)2 — kq1/d2 = kq2/9d2 — q2=9q1 — R- E.
75- a) Enquanto estiverem entre as placas ficam sujeitos a um campo elétrico E e consequentemente à uma força elétrica Fe relacionadas por E=Fe/q=Fe/e — Fe=e.E — desprezadas as ações gravitacionais, a força elétrica é a força resultante FR sobre esses elétrons e, pela segunda lei de Newton FR=m.a — Fe = FR — e.E = m.a — a=e.E/m.
b) A parcela horizontal da velocidade (eixo x) permanece constante (lançamento oblíquo) e igual Vx=Vo=constante e trata-se de um movimento retilíneo uniforme de equação x = xo + Vx.t — entre as placas x=L — L = 0 + Vo.t — t=L/Vo.
c) Enquanto os elétrons estão entre as placas surge sobre eles uma força elétrica, vertical e para cima (Fe e E tem mesma direção mas sentidos contrários pois elétrons possuem cargas negativas) — essa força age sobre os elétrons
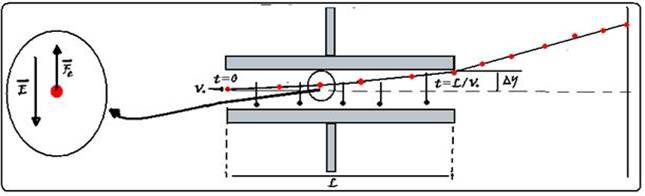
enquanto estiverem entre as placa durante t=L/Vo — como num lançamento obliquo, o movimento vertical para cima é um movimento uniformemente variado (acelerado com a=eE/m) de equação horária — y = yo + Voyt + at2/2 — y=∆y=0 + 0.t + (e.E/m).(L/Vo)2/2 — ∆y=e.E.L2/2mVo2.
d) Equação da velocidade do MUV, na direção vertical — Vy = Voy + a.t — Vy=0 + (e.E/m).(L/Vo) — Vy=e.E.L/m.Vo.
Linhas de força (de campo) – Potencial eletrostático
53- A) Para quebrar a rigidez dielétrica do ar e ocorrer descarga elétrica a maior intensidade do campo elétrico deve superar E=3.106Vm — d=3km=3.103m — E=Vd — 3.106=V/3.103 — V=9.109V ou V=9nV.
B) Se cada raio gera energia de 109J, 3 raios liberarão uma energia de W=3.109J — potência em ∆t=1s — P=W/∆t=
3.109/1 — P=3.109W ou P=3nW.
C) n=Ptotal/P1 raio=1,5.1010/109=1,5.10=15 raios.
54- Equilíbrio eletrostático entre dois condutores – Sejam dois condutores esféricos A e B, de raios RA e RB respectivamente, com cargas elétricas QA e QB e potenciais elétricos diferentes VA e VB (fig. I) — unindo-os por um fio condutor ou encostando-os haverá passagem de cargas elétricas entre eles até que seja atingido o equilíbrio
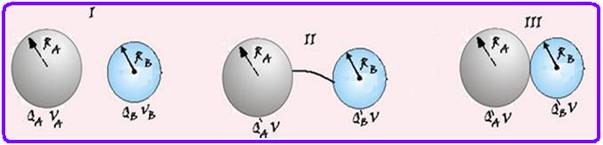
eletrostático quando atingem o mesmo potencial V — sejam Q’A e Q’B as novas cargas após o contato. Têm-se duas condições — A soma algébrica das cargas antes do contato é a mesma que a soma algébrica das cargas depois do contato — QA + QB=Q’A + Q’B — os potenciais são os mesmos após o contato — V=KQ’A/RA — V=KQ’B/RB — KQ’A/RA = KQ’B/RB — Q’A/Q’B=RA/RB — observe que, se RA=RB — Q’A=Q’B=(QA + QB)/2.
Observe na expressão Q’A/Q’B = RA/RB que, como a soma das cargas elétricas antes e depois do contato é a mesma, a relação Q’A/Q’B é constante — assim, se RA>RB, obrigatoriamente Q’A > Q’B — R- D.
Superfícies equipotenciais – trabalho da força eletrostática
50- No capacitor plano considerado, a diferença de potencial entre as placas é de U=1V e a distância entre as placas vale d=1μm=1.10-6m — num capacitor plano é válida a relação:
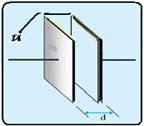
U=E.d — 1=E.10-6 — E=1/10-6 — E=106V/m — E=1MV/m — R- A.
51- O trabalho (W) realizado pela força elétrica no transporte dessa carga de q=10C da nuvem para o solo é igual à energia elétrica (E) liberada pelo raio nessa transferência e, ela ocorre devido à diferença de potencial U=100.106V=10.107V entre a nuvem e o solo — E=W=q.U=10×10.107=100.107J — regra de três — 1J – 3.10-7 kWh — 100x107J – W — W=E=3.10-7.100.107=300kWh — R- C.