Resolução Comentada – Vestibulares Recentes – Eletromagnetismo

01-

Inseparabilidade dos polos magnéticos

Se você quebrar um imã (corte transversal) e em seguida continuar dividindo os imãs

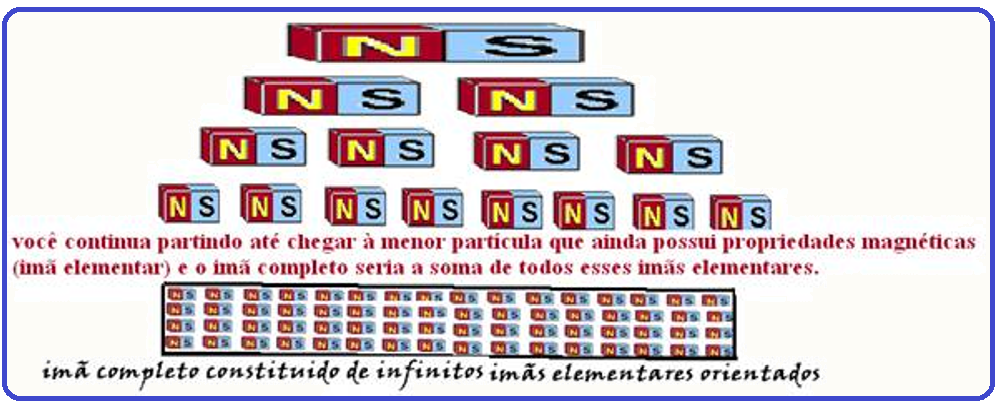
resultantes, você observará que cada pedaço partido continuará sendo um novo imã com dois polos, Norte e Sul de maneira que cada pedaço atraia o outro. Não existem polos isolados.

Se você partir um imã conforme a figura abaixo (corte longitudinal), a força entre eles será de repulsão.

R- E

02-

I- Verdadeira

Aurora polar – Trata-se de um fenômeno luminoso gerado nas camadas mais elevadas da atmosfera (400 a 800 quilômetros de altura) e observado com maior freqüência nas regiões próximas aos polos do planeta. No Polo Norte, chama-se aurora boreal; no Sul, austral.

Essas auroras ocorrem quando partículas elétricas (fótons e elétrons) provenientes do Sol chegam às vizinhanças da Terra e são atraídas por seu campo magnético. Ao alcançarem a atmosfera, essas partículas se chocam com os átomos de oxigênio e nitrogênio – num processo semelhante à ionização (eletrificação) de gases que faz acender o tubo de uma lâmpada fluorescente.

II- Verdadeira

A Terra se comporta como um grande imã onde o polo Sul magnético está aproximadamente localizado no polo Norte geográfico e vice versa.

Se você pendurar um imã em forma de barra pelo seu centro ou observar a agulha magnética de uma bússola você verá que seus polos ficam sempre alinhados na direção norte-sul.

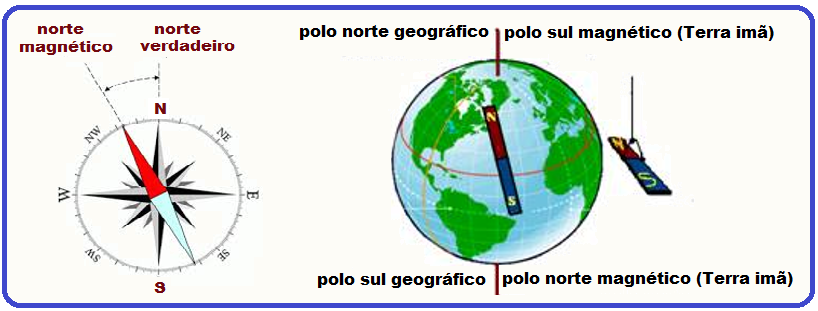
O polo que indicar o polo norte geográfico recebe o nome de polo norte e estará indicando o polo sul magnético da Terra.

O polo que indicar o polo sul geográfico recebe o nome de polo sul e estará indicando o polo norte magnético da Terra. Tudo isso ocorre porque polos de nomes opostos se atraem

III- Falsa

Analise na figura abaixo as linhas de indução do campo magnético terrestre e observe que a agulha magnética de uma bússola (indicação do campo magnético terrestre) tem a propriedade de se alinhar de acordo com as linhas do campo geomagnético.

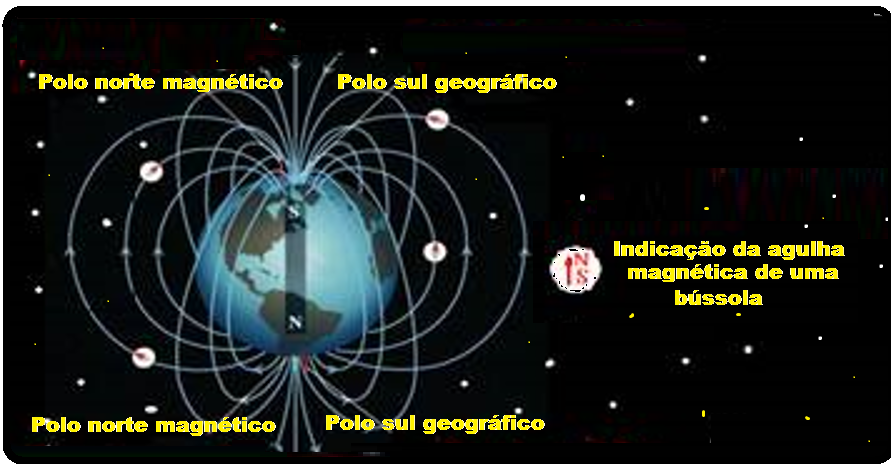
Observe na figura acima que o campo magnético terrestre, em cada ponto é tangente às linhas de indução, variando em direção e sentido e aumentando em módulo à medida que se aproxima dos polos.

R- B

03-

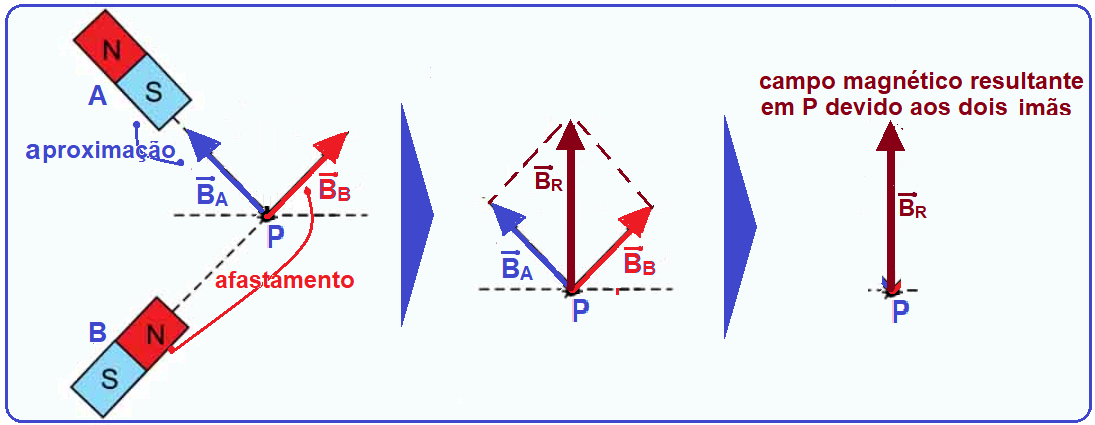
As linhas de campo magnético comportam-se como esboçado na figura abaixo:

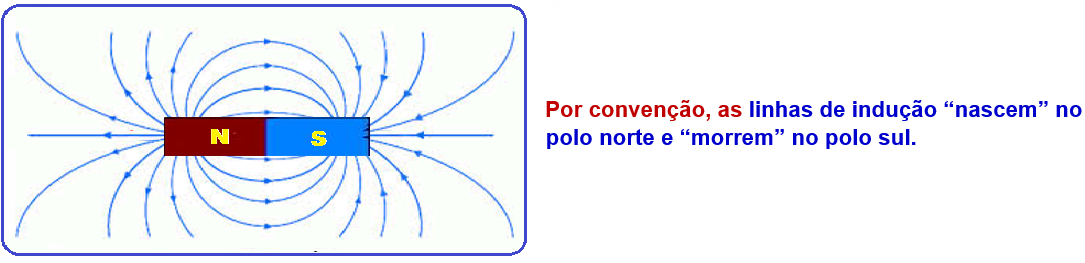
As linhas de campo magnético partem do polo norte em direção ao polo sul, exceto dentro do ímã, em que elas partem do polo sul para o norte, como é possível observar pela figura.

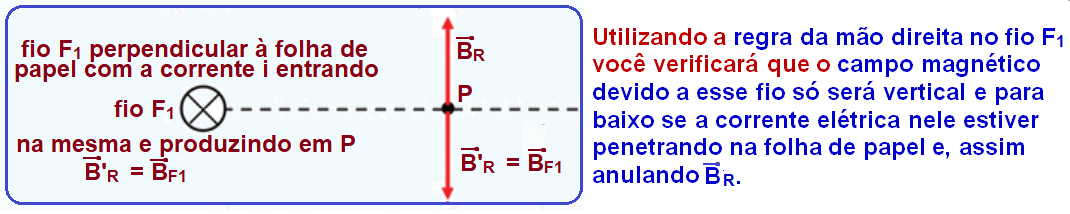
Observando a figura do enunciado, temos:

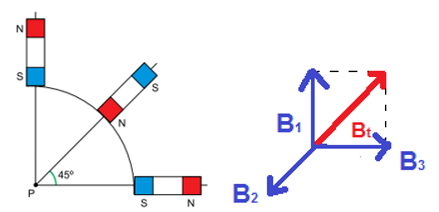
Em que os vetores B representam o campo de magnético, e suas orientações dependem da posição do ímã, sabendo que se o polo mais próximo for o norte, a linha de campo deve estar saindo, e se o sul for o polo mais próximo, a linha de campo de deve estar entrando no seu respectivo ímã. Para encontrar a resultante, devemos fazer a soma vetorial:

Na direção de , logo a alternativa correta é D.

04-

Veja abaixo um resumo da teoria:

Características do Vetor Campo Elétrico

Carga elétrica q lançada com velocidade lançada perpendicularmente às linhas de indução de um campo magnético uniforme

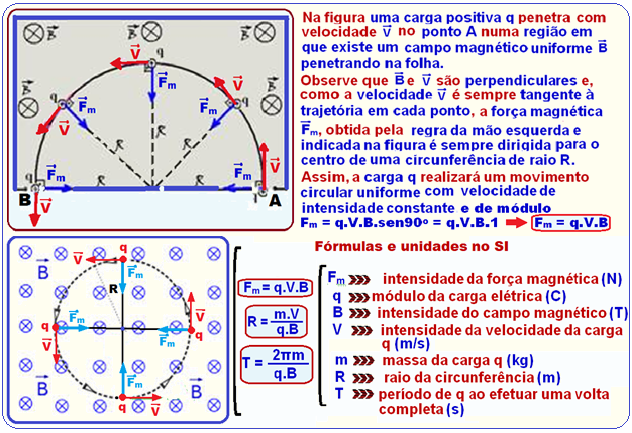
Força sobre q devido ao campo elétrico E = F/q F = q.E (I)

Força sobre q devido ao campo magnético F = q.V.B (II)

(I) = (II) q.E = q.V.B V = E/B.

R- A

05-

Carga elétrica q lançada com velocidade lançada perpendicularmente às linhas de indução de um campo magnético uniforme

São dados: q = 3,2µC = 3,2.10-6 C; V = 2.104 m/s; F = 1,6.102 N e B = ?

Fm = q.V.B 1,6.102 = 3,2.10-6.2.104.B 1,6.102 = 6,4.10-2.B B = 1,6.102/6,4.10-2 B = 0,25.104 = 2,5.103 T.

R – B

06-

Se você não domina a teoria ela está a seguir:

Carga elétrica q lançada com velocidade lançada perpendicularmente às linhas de indução de um campo magnético uniforme

Observe que, neste caso o ângulo entre e é 90o (são perpendiculares) e que sen90o = 1.

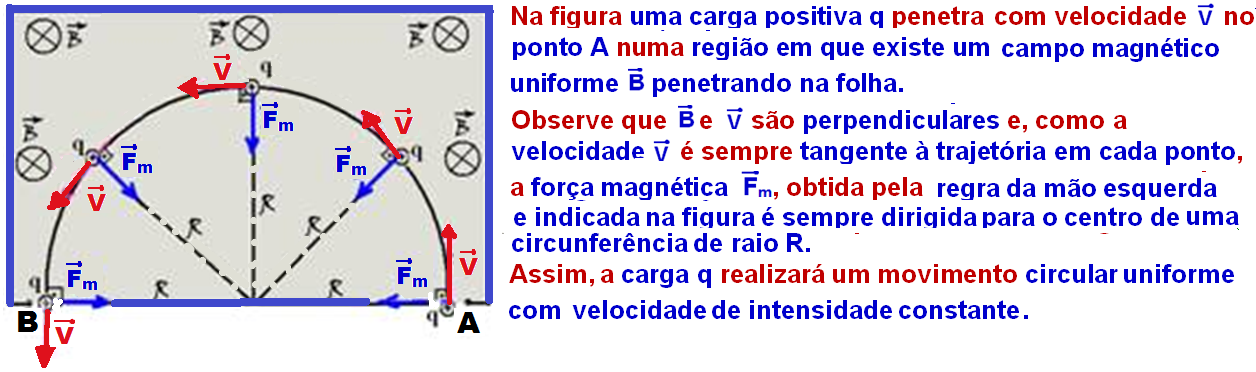
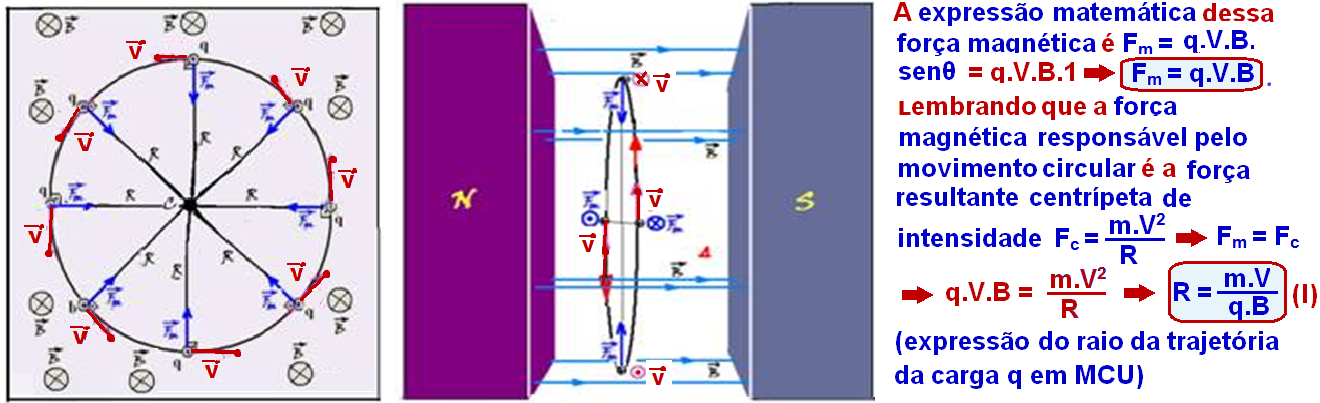
O período T (tempo que a carga q demora para efetuar uma volta completa) é fornecido por V = ΔS / Δt numa volta completa ΔS = 2πR e Δt = T V = 2πR / T (II).

Substituindo II em I R = m. (2πR/T)/q.B T = 2πm/q.B (período do MCU).

Observe que o período (T) do movimento circular não depende da velocidade com que a partícula q penetra no campo magnético e nem do raio da circunferência.

01.Falso – são perpendiculares com ângulo sempre de 90o (veja teoria acima).

02 – Correto – Fm = q.v.B = 4.10-6.2.102.7.10-2 = 56.10-6 = 5,6.10-5 N.

04. Correto – veja teoria acima.

08- Correto – pelo enuncia a massa m e a e o módulo da velocidade v do feixe de partículas é constante e pelas expressões da energia cinética Ec = m.v2/2 e da quantidade de movimento Q = m.v você verifica que Ec e Q também são constantes.

16. Correto – veja na expressão R = q.B/m.v que o raio R é função da massa m, sendo B e v constantes.

R – ( 02 + 04 + 08 + 16) = 30

07-

Breve resumo da teoria

Regra da mão esquerda

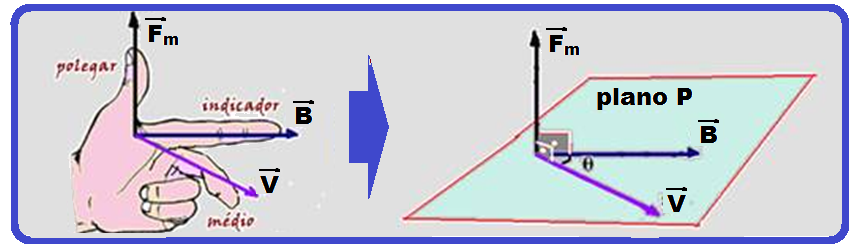
Aplicando a regra da mão esquerda no ponto onde o elétron (carga negativa) está penetrando na região de campo magnético você verificará que o campo magnético B está saindo da folha, mas como é carga negativa estará entrando. (lembre-se de que em cada ponto Vo é tangente à trajetória e F é dirigida para o centro da circunferência). “veja figura abaixo”.

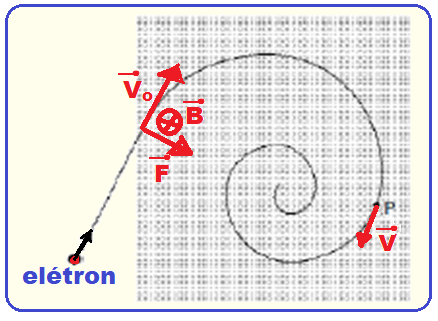
R- A

08-

Força magnética sobre carga elétrica

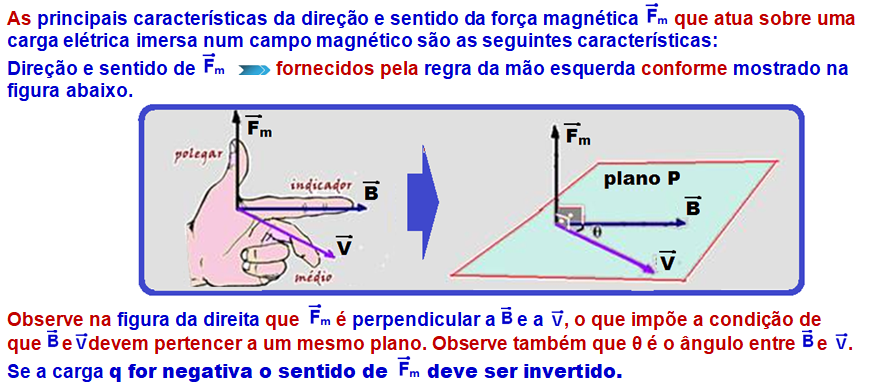
R- C

09-

Carga elétrica q lançada com velocidade lançada perpendicularmente às linhas de indução de um campo magnético uniforme

Observe que, neste caso o ângulo entre e é 90o (são perpendiculares) e que sen90o = 1.

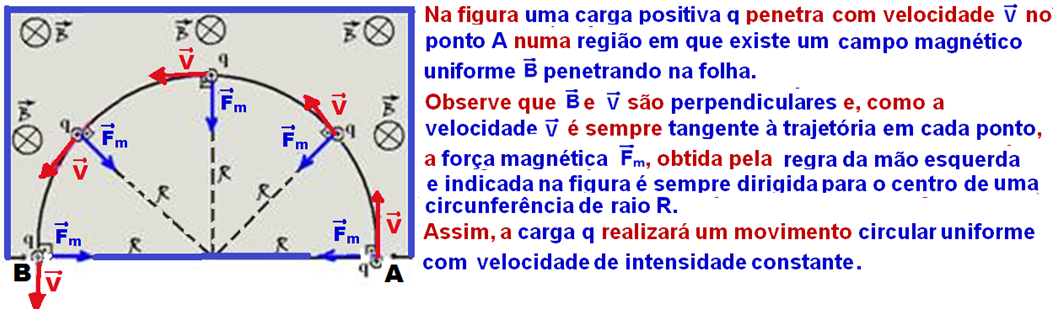
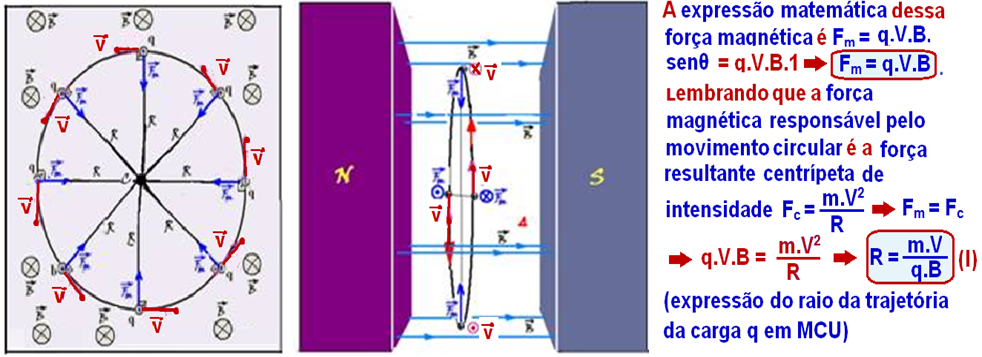
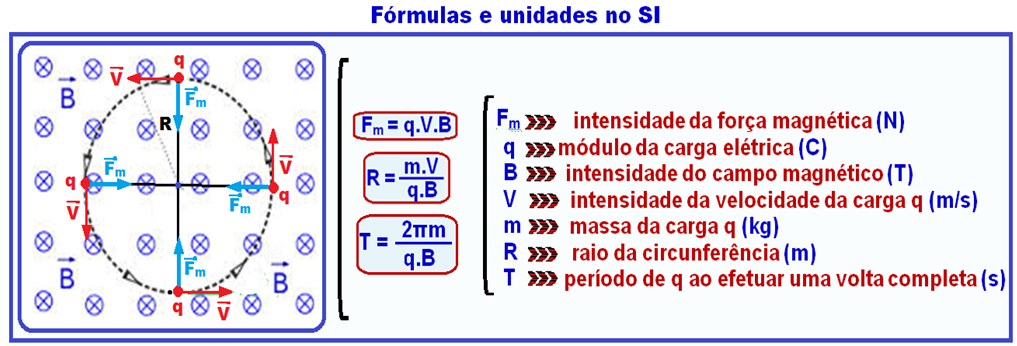
R- C

10-

Carga elétrica q lançada com velocidade lançada perpendicularmente às linhas de indução de um campo magnético uniforme

R- A

11-

Força magnética sobre uma carga móvel imersa num campo magnético

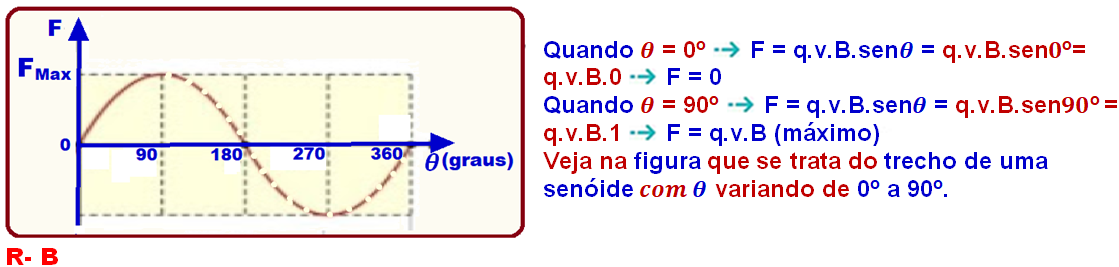
12-

Veja abaixo as duas condições para que a força magnética sobre a carga seja nula.

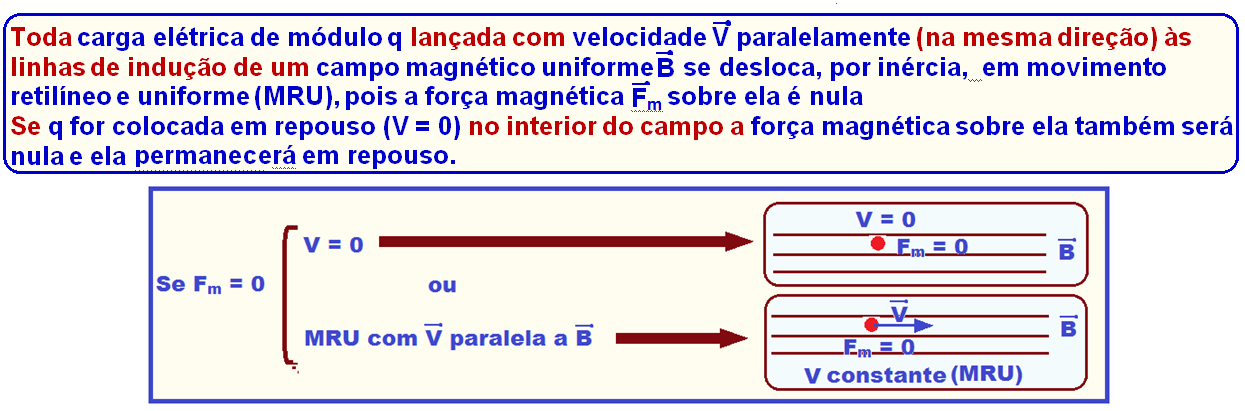
R- B

13-

Nesse caso precisamos lembrar de uma fórmula importante:

Isolando a velocidade:

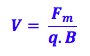Como a partícula se movimenta em linha reta quer dizer que as forças elétricas e magnéticas se anulam, ou seja, elas são iguais em intensidade, porém possuem sentidos contrários. Essa informação é fundamental, pois:

Fm = Fe

04 – Bom, sabemos que a cada 30 anos o Césio perde metade de sua massa inicial. 2077 é 60 anos depois de 2017, sendo que em 2017 já se passaram 30 anos, então a quantidade total de anos é 30 + 60 = 90 anos. Se a cada 30 anos se vai uma meia vida de Césio, então em 90 anos se vão 3 meias vidas. Isso equivale à metade da metade da metade da massa inicial, ou:

O que equivale à 1/8 da massa inicial, alternativa C.

14-

R- E

15-

Campo magnético originado por um condutor retilíneo extenso percorrido por corrente elétrica

Direção e sentido do vetor campo magnético

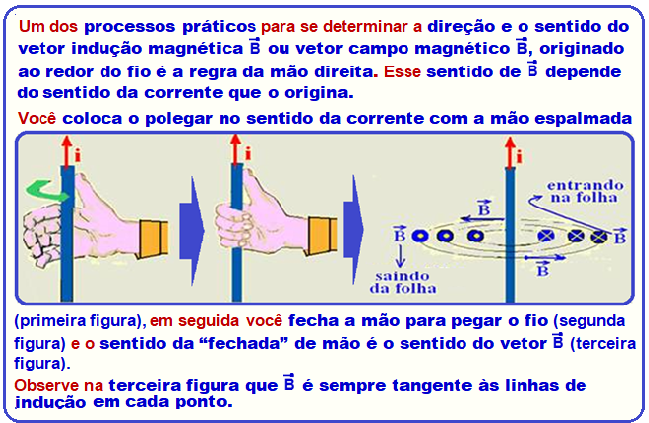
Utilizando a regra da mão direita em cada fio você verificará que o campo magnético resultante estará perpendicular ao plano determinado pelos fios, entrando nele.

R- A

16-

Se você não domina a teoria, ela está a seguir:

Força de interação entre dois fios condutores paralelos percorridos por corrente elétrica

Considere dois condutores retilíneos 1 e 2 percorridos, respectivamente por correntes elétricas i1 e i2, e separados por uma distância d. Tem-se duas situações:

As correntes elétricas tem mesmo sentido

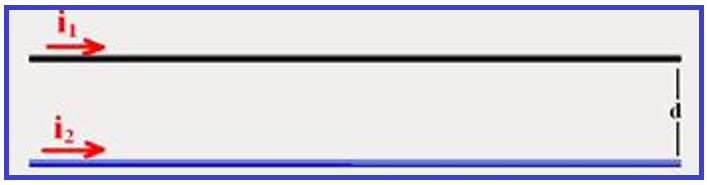
Utilizando a regra da mão direita, você determina B1 que é o vetor indução magnética que o condutor 1 produz onde está o condutor 2.

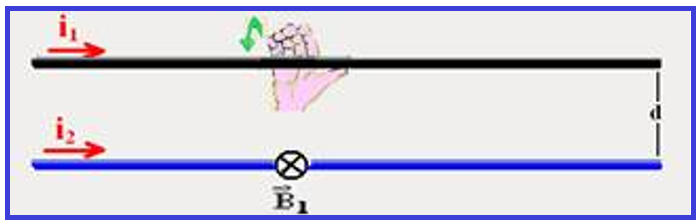
O condutor 2, imerso no campo magnético de B1 ficará sujeito a uma força magnética Fm2, fornecida pela regra da mão esquerda.

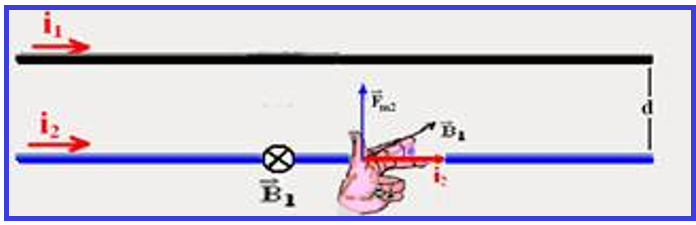
Assim, o condutor 2 fica sujeito a uma força magnética Fm2 vertical e para cima.

Analogamente, o condutor 2 origina, onde está o condutor 1, um campo magnético B2 que, fornecido pela regra da mão direita estará saindo da folha de papel.

Então surgirá sobre o condutor 1 uma força vertical e para baixo, fornecida pela regra da mão esquerda.

Situação final:

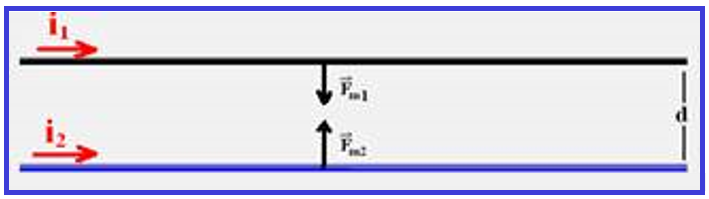
Se as correntes elétricas tiverem sentidos contrários, procedendo da mesma forma que no item anterior, você observará que os dois fios sofrem força de repulsão.

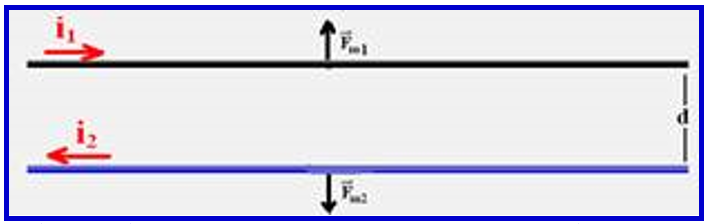
No caso do exercício, como as correntes possuem mesmo sentido a força elétrica entre eles será de

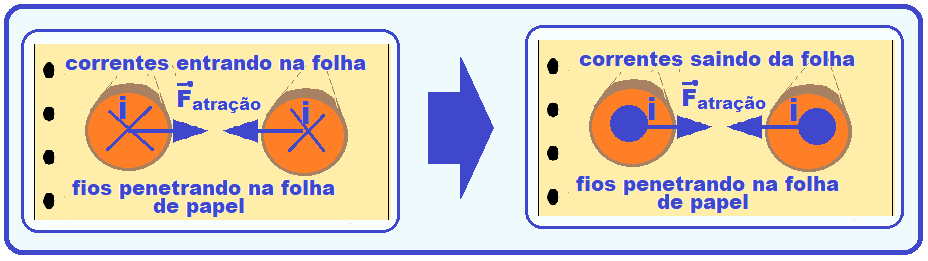
atração.

R- E

17-

Campo magnético originado por um condutor retilíneo extenso percorrido por corrente elétrica

Direção e sentido do vetor campo magnético

Intensidade do campo magnético

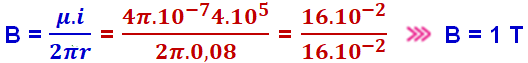
R- E

18-

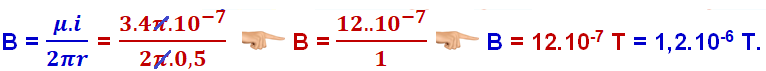
R- E

19-

Força de interação entre dois fios condutores paralelos percorridos por corrente elétrica

Considere dois condutores retilíneos 1 e 2 percorridos, respectivamente por correntes elétricas i1 e i2, e separados por uma distância d. Tem-se duas situações:

As correntes elétricas tem mesmo sentido

Utilizando a regra da mão direita, você determina B1 que é o vetor indução magnética que o condutor 1 produz onde está o condutor 2.

O condutor 2, imerso no campo magnético de B1 ficará sujeito a uma força magnética Fm2, fornecida pela regra da mão esquerda.

Assim, o condutor 2 fica sujeito a uma força magnética Fm2 vertical e para cima.

Analogamente, o condutor 2 origina, onde está o condutor 1, um campo magnético B2 que, fornecido pela regra da mão direita estará saindo da folha de papel.

Então surgirá sobre o condutor 1 uma força vertical e para baixo, fornecida pela regra da mão esquerda.

Situação final:

Se as correntes elétricas tiverem sentidos contrários, procedendo da mesma forma que no item anterior, você observará que os dois fios sofrem força de repulsão.

Como no exercício as correntes elétricas possuem sentidos opostos a força entre os fios será de repulsão (interação repulsiva).

Intensidade dessa força, de atração ou de repulsão:

R- A

Observação: Essas forças possuem a mesma intensidade (módulo), pois constituem par ação e reação (mesma intensidade, mesma direção mas sentidos contrários).

20-

Embaixo está um resumo. Se estiver interessado, a teoria completa encontra-se em fisicaevestibular.com.br – Eletricidade – Eletromagnetismo – Campo magnético originado por um condutor retilíneo extenso percorrido por corrente elétrica

21-

O leitor da etiqueta emite um campo de radiofrequência (por meio de ondas magnéticas de rádio) à etiqueta eletrônica identificadora (tags) que retornam esses sinais de radiofrequência para os leitores.

Os leitores captam essas informações quando o fluxo magnético variável produzido no retorno dessas ondas faz surgir na bobina (espira) do leitor uma corrente elétrica induzida.

Pela Lei de Faraday essa corrente elétrica origina na bobina um campo magnético também variável que é detectado pelo leitor que registra essas informações.

R- C

22-

Primeiro usamos a fórmula para calcular o fluxo ΦB de um campo magnético uniforme B passando por uma área A:

A área mencionada acima é a área do retângulo por onde passa o campo magnético, como apenas uma parte da espira está sobre o campo, dizemos que a área é então o produto do lado b por um comprimento x que depende do tempo, pois conforme a espira se move para dentro do campo, esse x aumenta, assim a relação acima se torna:

23-

Observando a imagem:

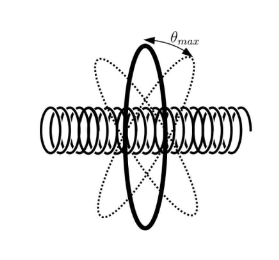
De acordo com a Lei de Faraday temos que:

Portanto a força eletromotriz induzida irá depender da variação do fluxo magnético, precisamos encontra-lo. O fluxo magnético já depende de:

No caso de um solenoide o seu campo magnético é:

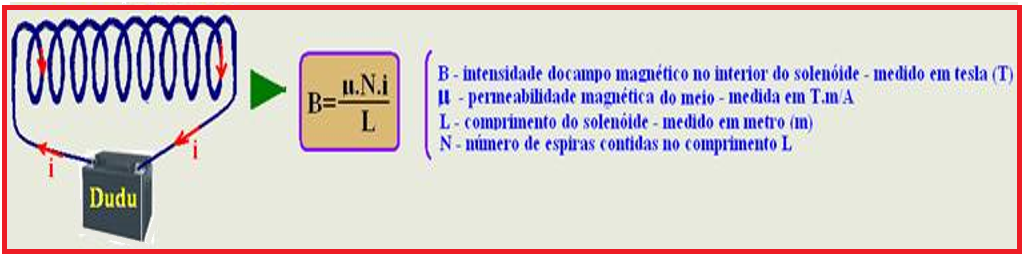
Como a corrente varia com o tempo pela equação i = Kt. Observe também que o enunciado informa que a espira tem N voltas por unidade de comprimento, ou seja, n = N/L voltas/unidade de comprimento:

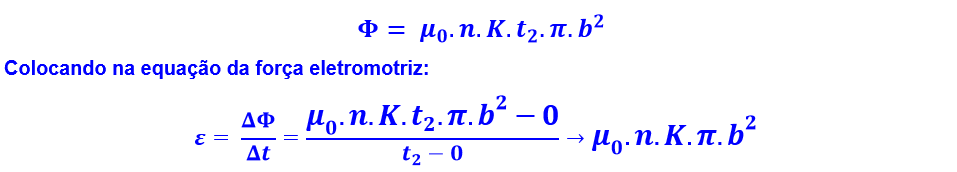
Como sabemos a fem induzida, só nos resta saber a intensidade da corrente, podemos usar a lei de Ohm:

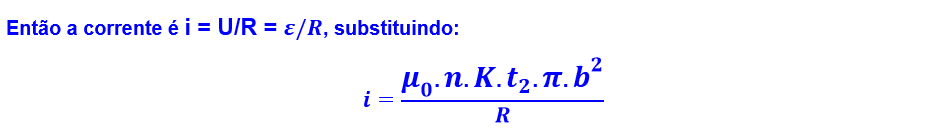
Alterativa correta é a B.

24-

Força eletromotriz induzida pelo movimento

Força eletromotriz gerada por um condutor móvel num campo elétrico uniforme

Força eletromotriz ε gerada por um condutor móvel imerso num campo elétrico uniforme esse condutor tem o comportamento de um gerador mecânico de eletricidade de fem ε.

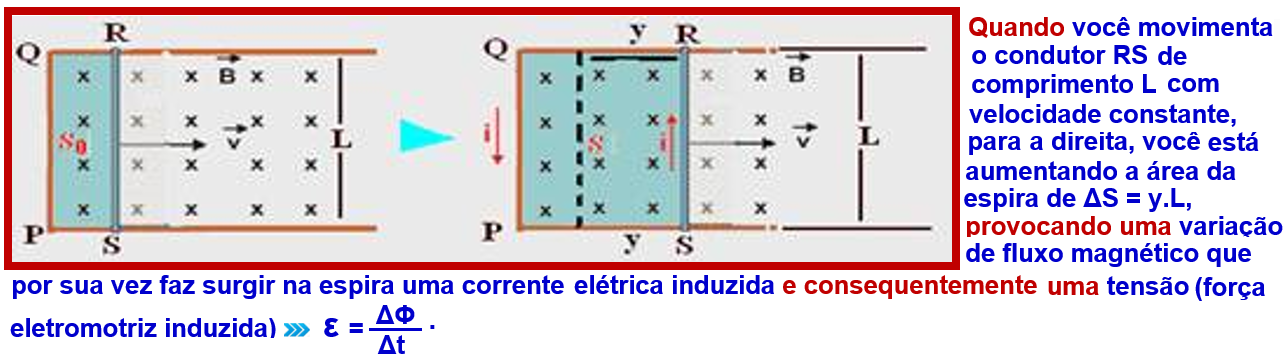
O sentido da corrente elétrica induzida é fornecido pela lei de Lenz “a força eletromotriz induzida e a corrente induzida geram um fluxo magnético que se opõe à variação do fluxo causador da indução”.

I. Verdadeira – Ao deslocarmos o circuito e o ímã juntos em sentidos contrários, ao longo da direção y surge corrente no circuito porque está ocorrendo a variação (no caso diminuição) da área da espira.

II. Verdadeira – está também variando a área da espira.

III. Verdadeira – veja teoria acima.

IV. Falsa – não ocorre variação da área.

V. Fasa – veja IV.

R- C

25-

Corrente elétrica induzida

Para que você entenda o fenômeno da indução eletromagnética, considere uma única espira e

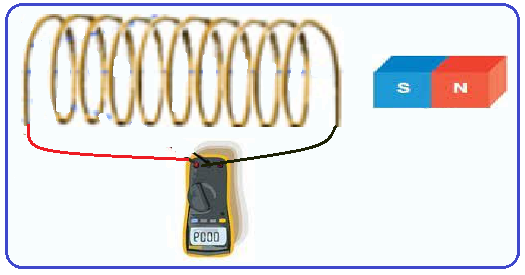
um imã permanente. Quando você aproxima o imã da espira, o número de linhas de indução do imã que penetram na espira (fluxo magnético) aumenta, fazendo surgir na espira uma corrente elétrica induzida num determinado sentido.

Quando você afasta o imã da espira, o número de linhas de indução do imã (fluxo magnético) que penetram na espira diminui, fazendo surgir na espira uma corrente elétrica induzida com sentido oposto ao anterior.

Com o imã imóvel, o número de linhas de indução que penetram na espira (fluxo magnético) não muda, não existindo corrente elétrica induzida.

Você obteria o mesmo resultado acima, mantendo o imã fixo e movendo a espira ou movendo os dois, pois não importa quem se movimente, mas que haja variação de fluxo magnético através da espira, o que só ocorre se a velocidade relativa entre eles for diferente de zero.

O mesmo será válido se, em vez de uma espira você tivesse um solenoide ou bobina (várias espiras circulares de mesmo raio, concêntricas e interligadas)

R- E

26-

Se, ao fazer o gerador funcionar, o estudante obteve uma tensão máxima V e uma corrente de curto-circuito i, então a tensão máxima U é a força eletromotriz induzida do gerador, ou seja, V = .

Para n espiras a força eletromotriz induzida é fornecida por = n. = n. .

Para variar o fluxo magnético no interior da associação de espiras, podemos mudar o valor do campo magnético (B), da área (S), do ângulo de giro () ou o número de espiras (n).

Mas o enunciado pede também que, além de dobrar deve-se manter constante a corrente de curto circuito icc que é fornecida por icc = , onde r é a resistência interna devida às n espiras, o que só pode acontecer se você dobrar r.

Mas, pela segunda lei de Ohm a resistência r é fornecida por:

Como o exercício pede o dobro da d.d.p. induzida, sem mudar a corrente de curto-circuito icc, além de dobrarmos o fluxo , devemos dobrar também a resistência r do material. Isso pode acontecer através da mudança do material , do comprimento L ou da área S de seção do fio.

A única opção que satisfaz as duas condições ao mesmo tempo é dobrar o número n de espiras, o que dobra a d.d.p. e a resistência do material ao mesmo tempo, e que mantém a corrente de curto inalterada.

R- A

27-

Se você não domina a teoria pode encontra-la em fisicaevestibular.com.br – Eletricidade – Eletromagnetismo -força eletromotriz induzida.

Com x variando entre 0 e L (x < 0 < L), espira entrando na região do campo até ficar totalmente imersa, então a variação de fluxo magnético no interior da espira está aumentando.

Nesse caso, pela lei de Lenz, deve surgir um fluxo magnético que se oponha a esse aumento de fluxo, ou seja, deve surgir um fluxo magnético que esteja saindo da folha.

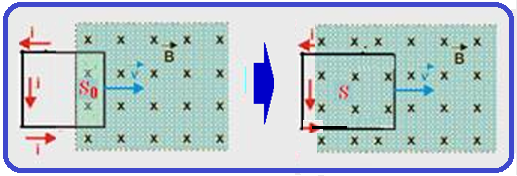
Com saindo da folha, usando a regra da mão direita, o sentido da corrente elétrica induzida está indicado nas figuras acima (sentido anti horário).

Enquanto a espira estiver totalmente imersa no interior da região do campo magnético (x < L< 3L),

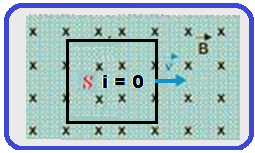
a corrente elétrica induzida é nula (não ocorre variação de fluxo magnético no interior da espira).

Com x variando entre 0 e L (3L < x < 4L), espira saindo região do campo até ficar totalmente fora dessa região, então a variação de fluxo magnético no interior da espira está diminuindo.

Nesse caso, pela lei de Lenz, deve surgir um fluxo magnético que se oponha a essa diminuição de fluxo, ou seja, deve surgir um fluxo magnético que esteja entrando na folha.

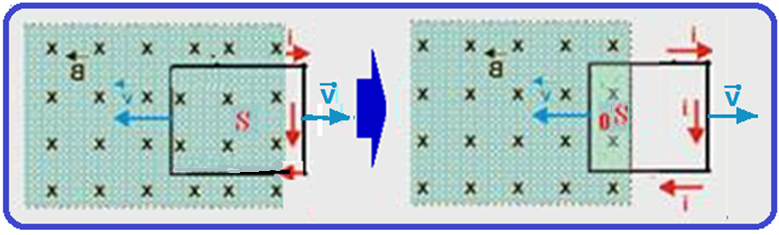
Com entrando da folha, usando a regra da mão direita, o sentido da corrente elétrica induzida está indicado nas figuras acima (sentido horário).

R- C

28-

Força eletromotriz induzida pelo movimento

Força eletromotriz gerada por um condutor móvel num campo elétrico uniforme

Força eletromotriz ε gerada por um condutor móvel imerso num campo elétrico uniforme esse condutor tem o comportamento de um gerador mecânico de eletricidade de fem ε.

São fornecidos: módulo do campo magnético B = 6,0 T; comprimento da barra condutora L = 1,0 m e velocidade de deslocamento da barra condutora v = 2 m/s.

Cálculo da força eletromotriz induzida () na barra condutora pela expressão = B.L.v = 6.1.2

= 12 V.

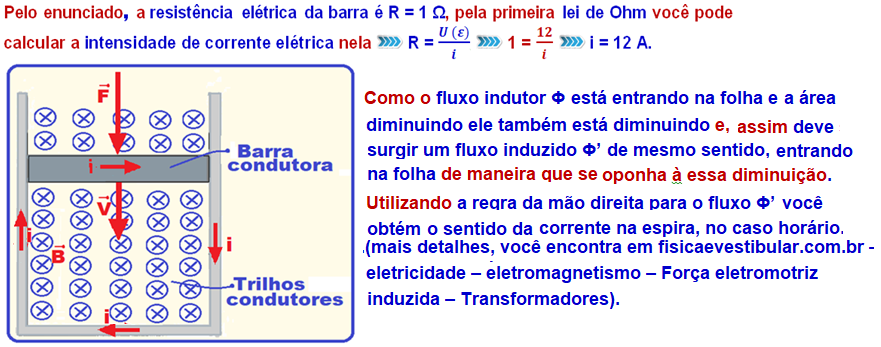
Estando a barra descendo com velocidade constante (equilíbrio dinâmico “força resultante nula”) então deve surgir sobre ela uma força magnética de intensidade Fm (vertical e para cima) que deve anular a força externa de intensidade F (vertical e para baixo).

Essa força magnética tem as seguintes características:

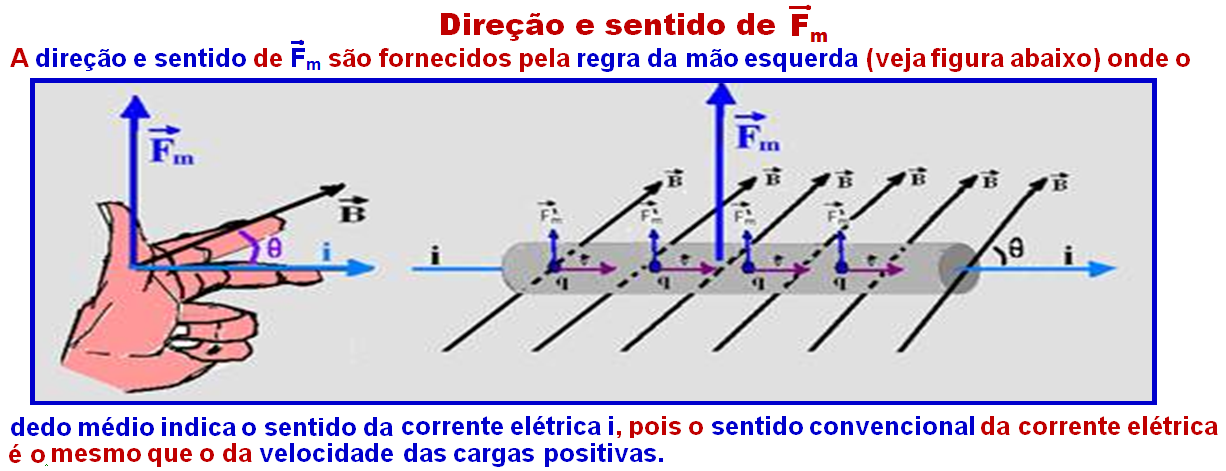
No caso do exercício a força magnética tem direção vertical e sentido para cima (figura abaixo).

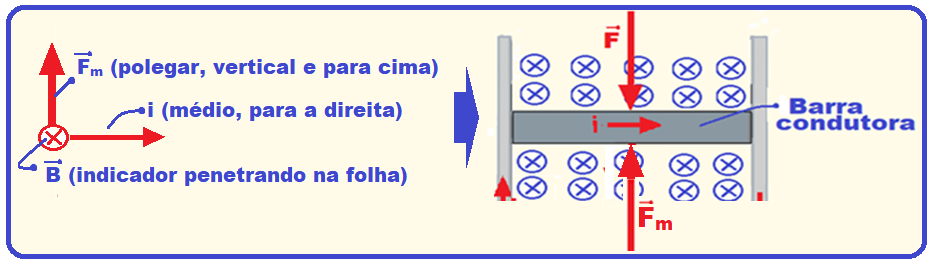
Cálculo da intensidade da força magnética pela expressão Fm = B.i.L.sensendo dados: B = 6 T; i = 12 A; L = 1 m e = 90o:

Fm = 6.12.1.1 Fm = 72 N.

R – E