Resolução Comentada ELETROMAGNETISMO – 2013 – 2014
Resolução Comentada
ELETROMAGNETISMO – 2013 – 2014
01- Veja na figura abaixo a regra da mão esquerda colocada no ponto de entrada das carga e que é
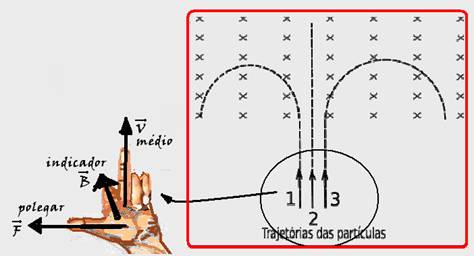
válida para carga positiva, onde a força magnética está desviando a carga para a esquerda — para a carga negativa a força tem mesma direção mas sentido contrário (para a direita) e a partícula neutra não sofre desvio — R- E.
02- Carga elétrica q lançada com velocidade ![]() lançada perpendicularmente às linhas de indução de um campo magnético uniforme
lançada perpendicularmente às linhas de indução de um campo magnético uniforme ![]() — observe que, neste caso o ângulo entre
— observe que, neste caso o ângulo entre ![]() e
e ![]() é 90o e que sen90o=1.
é 90o e que sen90o=1.
Na figura abaixo uma carga positiva q penetra com velocidade ![]() numa região em que existe um campo magnético uniforme
numa região em que existe um campo magnético uniforme ![]() saindo da folha. Observe que
saindo da folha. Observe que ![]() e
e ![]() são perpendiculares e, como a velocidade
são perpendiculares e, como a velocidade ![]() é sempre tangente à trajetória em cada ponto, a força magnética
é sempre tangente à trajetória em cada ponto, a força magnética ![]() , obtida pela regra da mão esquerda e indicada na figura é sempre dirigida para o centro de uma
, obtida pela regra da mão esquerda e indicada na figura é sempre dirigida para o centro de uma
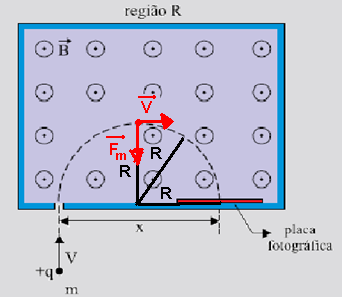
circunferência de raio R. Assim, a carga q realizará um movimento circular uniforme com velocidade de intensidade constante .

A expressão matemática dessa força magnética é Fm=q.V.B.senθ=q.V.B.1 — Fm=q.V.B — lembrando que a força magnéticaFm é responsável pelo movimento circular é a força resultante centrípeta de intensidade Fc=m.V2/R — Fm=Fc — q.V.B=m.V2/R — observe na figura acima que R=x/2 — q.B=m.V/x/2 — qBx/2=mV — m=qBx/2V.
R- E
03- Você está no eixo Z observando o sistema de eixos cartesianos de cima para baixo e verá a situação conforme a figura 1 — nela a corrente elétrica i no fio 1 está entrando na folha (plano XY) e a corrente no fio 2 saindo da mesma — utilizando a regra da mão direita, onde você coloca o polegar no sentido da corrente com a mão espalmada (primeira figura), em seguida você fecha a mão
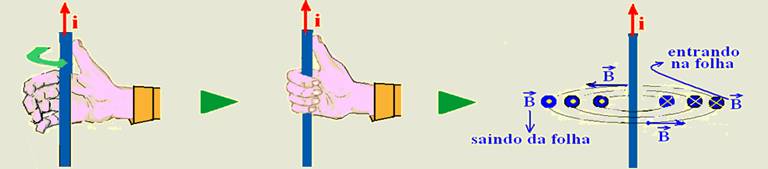
para pegar o fio (segunda figura) e o sentido da “fechada” de mão é o sentido do vetor![]() (terceira figura). Observe na terceira figura que
(terceira figura). Observe na terceira figura que ![]() é sempre tangente às linhas de indução em cada ponto — observe no fio 1 que utilizando a regra da mão direita as circunferências terão o sentido horário e no ponto P o vetor B1 originado pelo fio 1, que é tangente no ponto terá a direção e sentido indicados e no fio 2 que utilizando a regra da mão direita as circunferências terão o sentido anti horário e no ponto P o vetor B2 originado pelo fio 2, que é tangente no ponto terá a direção e sentido indicados e — a figura 2 mostra o vetor campo magnético
é sempre tangente às linhas de indução em cada ponto — observe no fio 1 que utilizando a regra da mão direita as circunferências terão o sentido horário e no ponto P o vetor B1 originado pelo fio 1, que é tangente no ponto terá a direção e sentido indicados e no fio 2 que utilizando a regra da mão direita as circunferências terão o sentido anti horário e no ponto P o vetor B2 originado pelo fio 2, que é tangente no ponto terá a direção e sentido indicados e — a figura 2 mostra o vetor campo magnético
resultante em P e a o vetor velocidade da carga q aí lançada — observe que B1=B2=B por simetria —
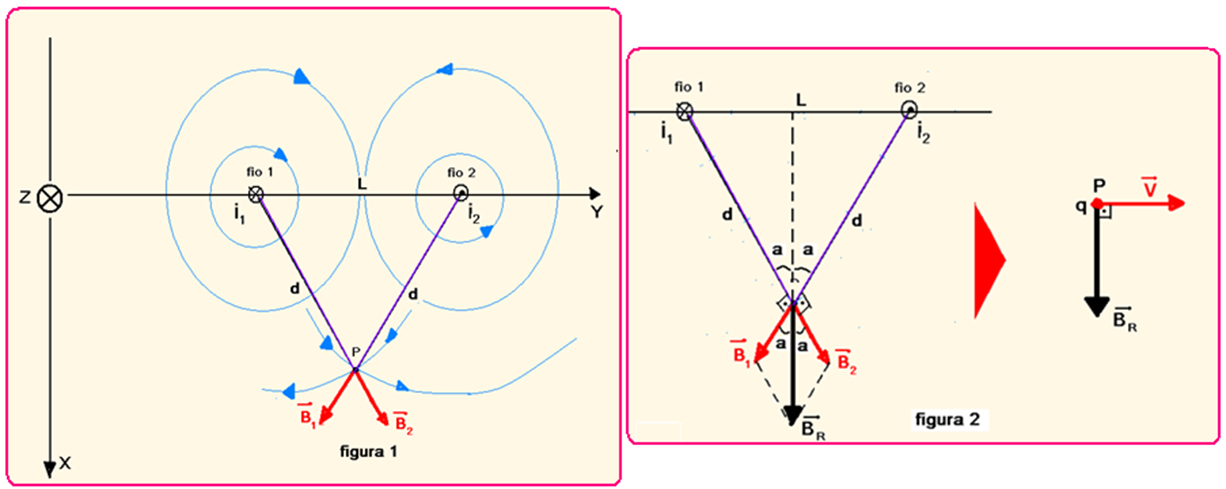
BR=B1cos a + B2cosa —BR=2Bcosa — B=µi/2πd — BR=2.µi/2πd.cosa — cosa=(L/2)/d — cosa=L/2d — BR= BR=2.µi/2πd.(L/2d) — BR= µiL/2πd2 (I) — força magnética que age sobre a carga q com velocidade V, perpendicular a BR — Fm=q.V.BR.sen90o=q.V.BR.1 — Fm=qVBR(II) — substituindo (I) em (II) — Fm=q.V. (µiL/2πd2) — Fm= µiLqV/2πd2 — R- C
04- Força elétrica ![]() — quando uma carga elétrica q é colocada no interior de um campo elétrico uniforme
— quando uma carga elétrica q é colocada no interior de um campo elétrico uniforme ![]() surge sobre ela uma força elétrica
surge sobre ela uma força elétrica ![]() com as seguintes características:
com as seguintes características:

Sendo as cargas elétricas que penetram no campo elétrico uniforme ![]() positivas a força elétrica
positivas a força elétrica ![]() que
que
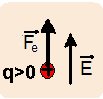
surgirásobre elas terá a mesma direção e sentido do campo, ou seja, vertical e para cima.
Força magnética ![]() — quando uma carga elétrica positiva q é colocada no interior de um campo magnético uniforme
— quando uma carga elétrica positiva q é colocada no interior de um campo magnético uniforme ![]() surge sobre ela uma força magnética
surge sobre ela uma força magnética ![]() com as seguintes características:
com as seguintes características:
Direção e sentido de ![]() – fornecidos pela regra da mão esquerda conforme mostrado na figura abaixo.
– fornecidos pela regra da mão esquerda conforme mostrado na figura abaixo.

Observe na figura da direita que ![]() é perpendicular a
é perpendicular a ![]() e a
e a ![]() , o que impõe a condição de que
, o que impõe a condição de que ![]() e
e ![]() devem pertencer a um mesmo plano. Observe também que θ é o ângulo entre
devem pertencer a um mesmo plano. Observe também que θ é o ângulo entre ![]() e
e ![]()
![]() Intensidade de
Intensidade de ![]() – é proporcional a q, V, B e ao senθ, obedecendo à equação:
– é proporcional a q, V, B e ao senθ, obedecendo à equação:

Pela regra da mão esquerda aplicada nas cargas ao penetrarem no campo magnético ![]() , a força
, a força
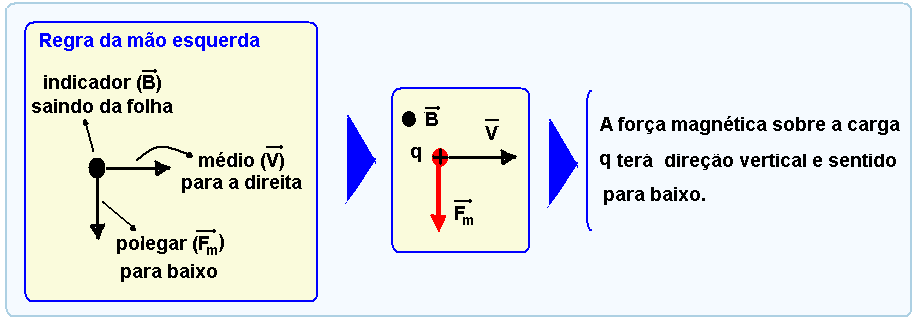
magnética ![]() que agirá sobre elas terá direção vertical e sentido para baixo (figura) e, sendo, pelo enunciado
que agirá sobre elas terá direção vertical e sentido para baixo (figura) e, sendo, pelo enunciado ![]() e
e ![]()
perpendiculares, o ângulo θ entre eles será de 90o e a intensidade de ![]() será Fm=q.V.B.sen90o — Fm=q.V.B.
será Fm=q.V.B.sen90o — Fm=q.V.B.
Análise de cada grupo, onde foram colocadas as forças elétrica ![]() e magnética
e magnética ![]() :
:
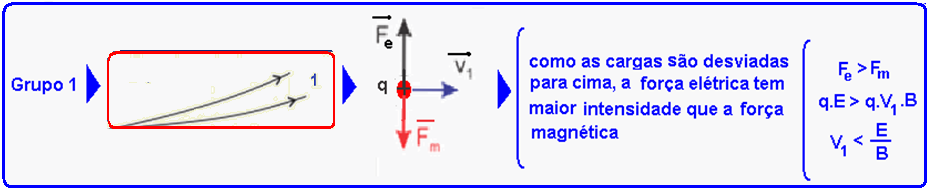
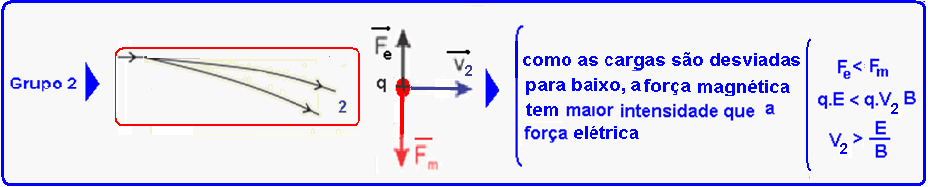
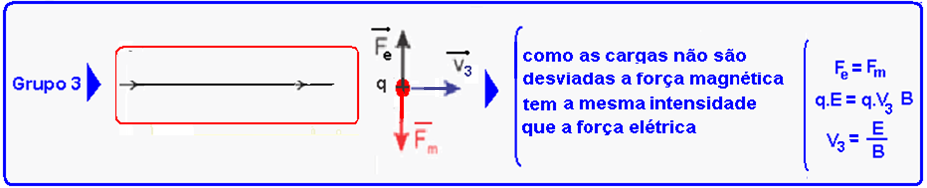
Conclusão: V1< V3< V2 e V3=E/B — R- E
05- Conforme o enunciado, existem dois dispositivos trabalhando no acionamento do atuador A, a lâmina bimetálica e o eletroímã:
Lâmina bimetálica – se surgir uma corrente elétrica de elevada intensidade percorrendo o disjuntor, a resistência R sofrerá um aquecimento, que será transmitido para o bimetal fazendo com que a temperatura do mesmo aumente e, pelo enunciado ele deverá tocar no atuador A, curvando-se para a
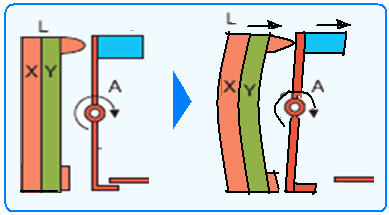
direita — para que isso ocorra o metal x deverá se ditar mais que o metal y, ou seja, ΔLx > ΔLy e, nessas condições αx > αy
pois, a expressão ΔL=Lo.α.Δө mostra que o coeficiente de dilatação α é diretamente proporcional à dilatação ΔL).
Eletroimã E – observe na figura (1) fornecida pelo enunciado que a corrente elétrica está circulando
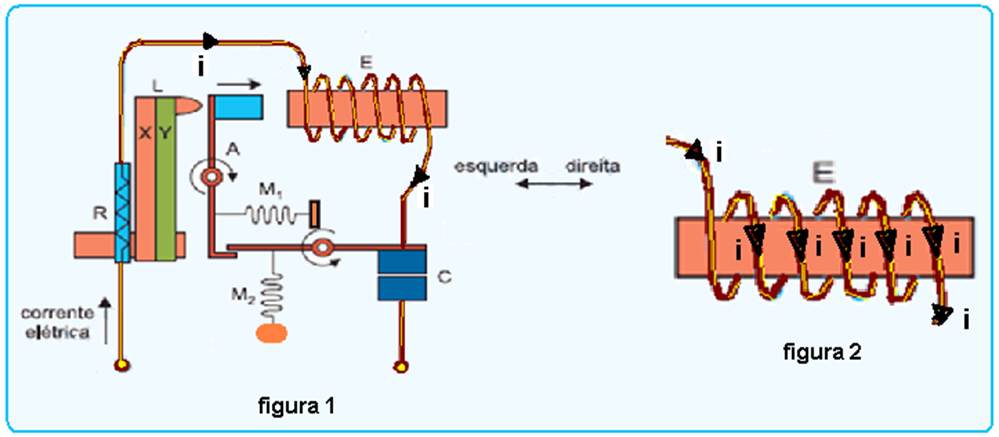
no eletroímã no sentido indicado na figura (2) — quando o solenoide (eletroímã) é percorrido por corrente elétrica, a configuração de suas linhas de indução é obtida pela reunião das configurações de cada espira o que equivale à configuração das linhas de indução de um imã natural.
O sentido das linhas de indução, que indicam o sentido do campo magnético no interior do solenoide (eletroímã) é fornecido pela regra da mão direita (polegar no sentido da corrente e o sentido do campo magnético ou das linhas de indução magnética é no sentido da “fechada” da mão) aplicada em uma de suas
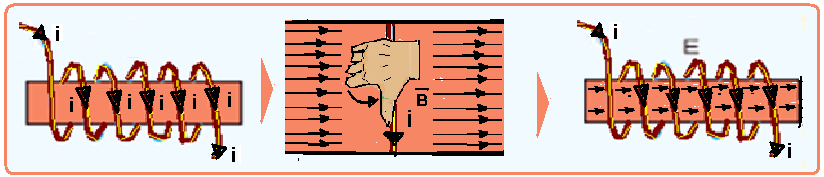
espiras (veja figuras acima) e em seu interior o campo magnético ![]() é praticamente uniforme e fora são linhas que saem do polo norte e chegam ao polo sul. Veja que o sentido do campo magnético criado ao longo do eixo do eletroímã apontará para a direta — R- C
é praticamente uniforme e fora são linhas que saem do polo norte e chegam ao polo sul. Veja que o sentido do campo magnético criado ao longo do eixo do eletroímã apontará para a direta — R- C
06- Carga elétrica q lançada com velocidade ![]() o perpendicularmente às linhas de indução de um campo magnético uniforme
o perpendicularmente às linhas de indução de um campo magnético uniforme ![]() — observe que, neste caso o ângulo entre
— observe que, neste caso o ângulo entre ![]() e
e ![]() é 90o e que sen90o=1.
é 90o e que sen90o=1.
Na figura abaixo uma carga positiva q penetra com velocidade ![]() no ponto A numa região em que existe um campo magnético uniforme
no ponto A numa região em que existe um campo magnético uniforme ![]() penetrando na folha. Observe que
penetrando na folha. Observe que ![]() e
e ![]() são perpendiculares e, como a velocidade
são perpendiculares e, como a velocidade ![]() é sempre tangente à trajetória em cada ponto, a força magnética
é sempre tangente à trajetória em cada ponto, a força magnética ![]() , obtida pela regra da mão esquerda e indicada na figura é sempre dirigida para o centro de uma circunferência de raio R.
, obtida pela regra da mão esquerda e indicada na figura é sempre dirigida para o centro de uma circunferência de raio R.
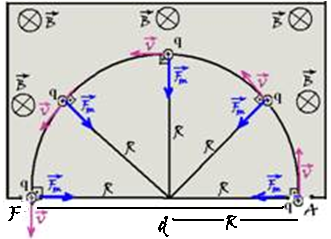
Assim, a carga q realizará um movimento circular uniforme com velocidade de intensidade constante .

A expressão matemática dessa força magnética é Fm=q.V.B.senθ=q.V.B.(1) — Fm=q.V.B — lembrando que a força magnética Fm é responsável pelo movimento circular é a força resultante centrípeta de intensidade Fc=m.V2/R — Fm=Fc — q.V.B=m.V2/R —
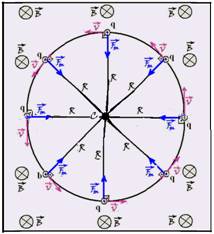
R=m.V/q.B (I) — o período T (tempo que a carga q demora para efetuar uma volta completa) é fornecido por — V=ΔS/Δt — numa volta completa — ΔS=2πR e Δt=T — V=2πR/T (II) — substituindo II em I —R=m. (2πR/T)/q.B — T=2πm/q.B (III) (tempo que o próton demora a efetuar uma volta completa)
Utilizando os dados fornecidos na equação (I):

R- B
07- Carga elétrica q lançada com velocidade ![]() lançada perpendicularmente às linhas de indução de um campo magnético uniforme
lançada perpendicularmente às linhas de indução de um campo magnético uniforme ![]() — observe que, neste caso o ângulo entre
— observe que, neste caso o ângulo entre ![]() e
e ![]() é 90o e que sen90o=1.
é 90o e que sen90o=1.
Na figura abaixo uma carga positiva q penetra com velocidade![]() no ponto A numa região em que existe um campo magnético uniforme
no ponto A numa região em que existe um campo magnético uniforme ![]() penetrando na folha. Observe que
penetrando na folha. Observe que ![]() e
e ![]() são perpendiculares e, como a velocidade
são perpendiculares e, como a velocidade ![]() é sempre tangente à trajetória em cada ponto, a força magnética
é sempre tangente à trajetória em cada ponto, a força magnética ![]() , obtida pela regra da mão esquerda e indicada na figura é sempre dirigida para o centro de
, obtida pela regra da mão esquerda e indicada na figura é sempre dirigida para o centro de
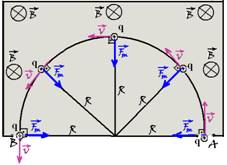
uma circunferência de raio R. Assim, a carga q realizará um movimento circular uniforme com velocidade de intensidade constante .

A expressão matemática dessa força magnética é Fm=q.V.B.senθ=q.V.B.1 — Fm=q.V.B — lembrando que a força magnética Fm é responsável pelo movimento circular é a força resultante centrípeta de


intensidade Fc=m.V2/R — Fm=Fc — q.V.B=m.V2/R — B=mV/qR — são dados — m=5.10-18 kg, q=8.10-6C, V=4.106m/s e R=5.103cm=50m — B=5.10-18x4.106/8.10-6.50=(20/400).10-6=0,05.10-6 —
B=5,0.10-8 T — R- D
08- Cargas elétricas em repouso não produzem campo magnético — R- E
09- Utilizando a regra da mão esquerda, indicador (campo magnético) penetrando na folha, médio (velocidade) vertical e para cima, o polegar indicará a força sobre o próton (carga positiva) para a esquerda (1 ou 2).
Sendo o elétron carga negativa a força sobre ele estará em sentido contrário ao do próton e será para a direita (4 ou 5).
Quando a radiação gama passa por um campo magnético ela não sofre desvio, pois não são partículas eletrizadas, mas sim radiações eletromagnéticas — assim essa radiação colide na posição 3.
Como o próton e o elétron penetram com a mesma velocidade e a massa do próton é muito maior que a massa do elétron, o próton sofre menor desvio atingindo a posição 1 e o elétron de menor massa, é mais desviado e atinge a posição 5.
R- E.
10- (V) Observe na figura abaixo a regra da mão esquerda com a força ![]() desviando a carga positiva
desviando a carga positiva
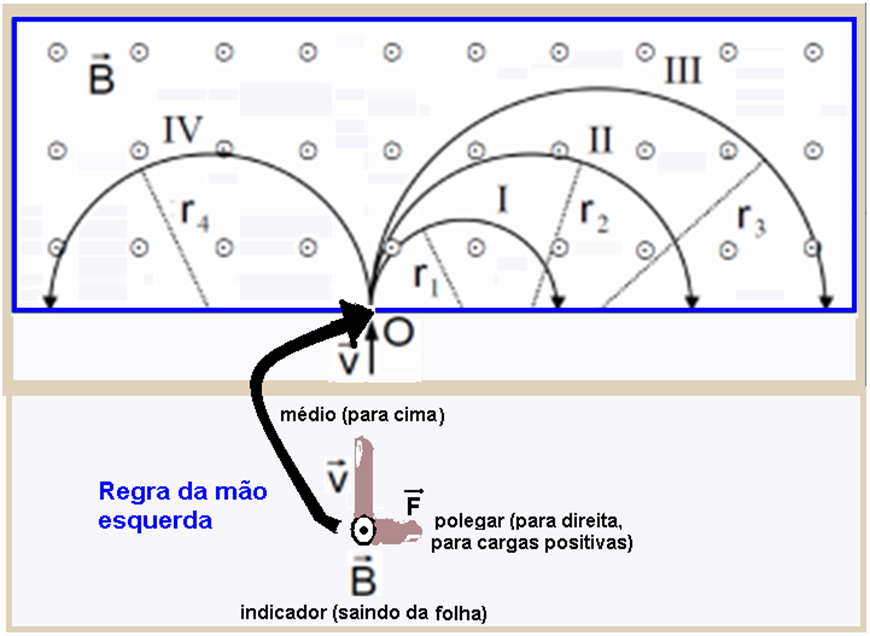
para a direita e a carga negativa para a esquerda.
(V) As partículas possuem cargas de sinais contrários já que a força magnética as desvia em sentidos opostos — Partículas com a mesma velocidade e a mesma carga elétrica ao penetrarem num campo magnético uniforme
com ![]() perpendicular a
perpendicular a![]() descrevem trajetórias circulares de raios diferentes, pois na expressão R=m.V/q.B apenas R e m são variáveis, sendo os outros parâmetros constantes. Observe na expressão que R e m são diretamente proporcionais. Maior massa, maior o raio da curva. — maior massa, menor valor q/m, pois q é a mesma para as duas cargas.
descrevem trajetórias circulares de raios diferentes, pois na expressão R=m.V/q.B apenas R e m são variáveis, sendo os outros parâmetros constantes. Observe na expressão que R e m são diretamente proporcionais. Maior massa, maior o raio da curva. — maior massa, menor valor q/m, pois q é a mesma para as duas cargas.
(F) na expressão R=m.V/q.B apenas R e q são variáveis, sendo os outros parâmetros constantes. Observe na expressão que R e q são inversamente proporcionais. Maior carga, menor o raio da curva e vice versa..
(F) Isolando o campo magnético B na expressão R=m.V/q.B, você obtém B=mV/qR onde B é inversamente proporcional a R, ou seja, quando um aumenta o outro diminui.
R- D
Imãs e campo magnético
60- Bússola – Trata-se de uma agulha magnética colocada na posição horizontal, suspensa pelo


centro de gravidade, indicando sempre a direção norte-sul — a Terra se comporta como um grande imã onde o polo Sul magnético está aproximadamente localizado no polo Norte geográfico e vice versa que no caso do exercício corresponde à barra cilíndrica imantada — se você pendurar um imã em forma de barra pelo seu centro ou observar a agulha magnética de uma bússola (caso do exercício) você verá que seus polos ficam sempre alinhados na direção norte-sul — o polo que indicar o polo norte geográfico recebe o nome de polo norte e estará indicando o polo sul magnético da Terra. O polo que indicar o polo sul geográfico recebe o nome de polo sul e estará indicando o polo norte magnético da Terra (barra imantada) — tudo isso ocorre porque polos de mesmo nome se atraem — pelo fornecido acima a alternativa correta é a D — R- D.
61– (V) Pelo enunciado, em Porto Alegre a direção do Sol nascente indicado pela bússola indica o nordeste geográfico e não o leste geográfico (a bússola indica a localização geográfica).
(F) A intensidade do campo magnético terrestre é maior que a de campos magnéticos locais.
(F) A bússola possui alta precisão e, por esse motivo é utilizada para determinar direções.
(V) A Terra se comporta como um grande imã onde o polo Sul magnético está aproximadamente localizado no polo Norte geográfico e vice versa — o polo Norte geográfico não coincide exatamente com o polo Sul magnético, distando um do outro aproximadamente 1.900km.
R- E.
62- Analise na figura abaixo as linhas de indução do campo magnético terrestre e observe que a agulha magnética de uma bússola tem a propriedade de se alinhar de acordo com as linhas do campo geomagnético.

Analisando a figura onde estão representadas estas linhas, observe que o pólo sul do ponteiro das bússolas aponta para o polo Sul geográfico, porque o Norte geográfico corresponde ao Sul magnético e pólios de nomes diferentes se atraem.
R- A.
63- I. Correta — a relação entre suas intensidades é E=F/q.
II. Falsa — carga em repouso (V=0) ou lançada com velocidade ![]() paralelamente às linhas de indução de um campo magnético uniforme
paralelamente às linhas de indução de um campo magnético uniforme ![]() — observe que, neste caso o ângulo entre
— observe que, neste caso o ângulo entre![]() e
e ![]() é θ=0o ou θ=180o e que sen0o=sen180o=0
é θ=0o ou θ=180o e que sen0o=sen180o=0
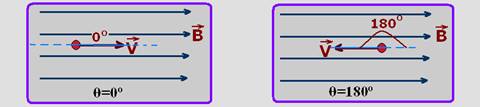
Fm=q.V.B.senθ=q.V.B.0 — Fm=0

III. Falsa — o campo magnético gerado pela Terra protege a mesma da radiação cósmica e partículas vindas do espaço.
IV. Falsa — veja (I)
V. Correta — qualquer corrente elétrica (cargas elétricas em movimento), mesmo de pequena intensidade, gera campo magnético.
R- C.
64- Para que os feixes de magnetita voltem a se orientar como na figura 1, o vetor dessa figura deve
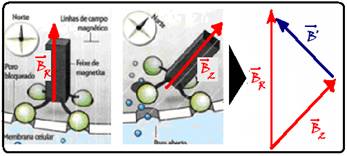
ser o vetor resultante ![]() — assim, o vetor
— assim, o vetor ![]() fornecido na figura 2 deve ser somado ao vetor pedido
fornecido na figura 2 deve ser somado ao vetor pedido ![]() de modo a fornecer o vetor resultante
de modo a fornecer o vetor resultante ![]() — veja na figura que B’ deve ser conforme na alternativa B — R- B.
— veja na figura que B’ deve ser conforme na alternativa B — R- B.
Força magnética sobre uma carga móvel imersa num campo magnético
61- Leia a teoria abaixo:
Carga elétrica q lançada com velocidade ![]() lançada perpendicularmente às linhas de indução de um campo magnético uniforme
lançada perpendicularmente às linhas de indução de um campo magnético uniforme ![]() — observe que, neste caso o ângulo entre
— observe que, neste caso o ângulo entre ![]() e
e ![]() é 90o e que sen90o=1.
é 90o e que sen90o=1.
Na figura abaixo uma carga positiva q penetra com velocidade ![]() no ponto A numa região em que existe um campo magnético uniforme
no ponto A numa região em que existe um campo magnético uniforme ![]() penetrando na folha. Observe que
penetrando na folha. Observe que ![]() e
e ![]() são perpendiculares e, como a velocidade
são perpendiculares e, como a velocidade ![]() é sempre tangente à trajetória em cada ponto, a força magnética
é sempre tangente à trajetória em cada ponto, a força magnética ![]() , obtida pela regra da mão esquerda e indicada na figura é
, obtida pela regra da mão esquerda e indicada na figura é

sempre dirigida para o centro de uma circunferência de raio R. Assim, a carga q realizará um movimento circular uniforme com velocidade de intensidade constante .

A expressão matemática dessa força magnética é Fm=q.V.B.senθ=q.V.B.1 — Fm=q.V.B — lembrando que a força magnética Fm é responsável pelo movimento circular é a força resultante centrípeta de intensidade Fc=m.V2/R —


Fm=Fc — q.V.B=m.V2/R —R=m.V/q.B.
No caso do exercício — dados — m=1,6.10-27kg — q=1,6.10-19C — V=1,5.106m/s — B=250.10-3T — R=1,6.10-27.1,5.106/1,6.10-19.250.10-3=2,4.10-21/400.10-22=0,006.101=0,06m=6cm — R- B.
62- Quando uma carga elétrica que se move com velocidade ![]() no interior de um campo magnético
no interior de um campo magnético ![]() sobre ela surge uma força de origem magnética
sobre ela surge uma força de origem magnética ![]() ( denominada força de Lorentz), com as seguintes características:
( denominada força de Lorentz), com as seguintes características:
![]() Direção e sentido de
Direção e sentido de ![]() – fornecidos pela regra da mão esquerda conforme mostrado na figura abaixo. Observe na
– fornecidos pela regra da mão esquerda conforme mostrado na figura abaixo. Observe na

figura da direita que ![]() é perpendicular a
é perpendicular a ![]() e a
e a ![]() , o que impõe a condição de que
, o que impõe a condição de que ![]() e
e ![]() devem pertencer a um mesmo plano. Observe também que θ é o ângulo entre
devem pertencer a um mesmo plano. Observe também que θ é o ângulo entre ![]() e
e ![]() .
.
![]() Intensidade de
Intensidade de ![]() – é proporcional a q, V, B e ao senθ, obedecendo à equação:
– é proporcional a q, V, B e ao senθ, obedecendo à equação:

Se a carga q for negativa o sentido da força magnética sobre ela é invertido.
Nas condições do exercício, as partículas sofrerão forças de mesma direção, mas como seus sinais são contrários, tais forças terão sentidos contrários — R- B.
63– Intensidade da força magnética ![]() sobre a carga é proporcional a q, V, B e ao senθ, obedecendo à equação:
sobre a carga é proporcional a q, V, B e ao senθ, obedecendo à equação:

Pelo enunciado o ângulo entre o campo magnético e a trajetória da carga é 90o (perpendiculares) — Fm=q.V.B.sen90o
— Fm=q,V.B.1=1,6.10-19.3.108.8=38,4.10-11N≈3,8.10-10N — R- A.
64- O campo magnético uniforme ![]() está saindo da folha de papel — no ponto F os íons estão penetrando com velocidade
está saindo da folha de papel — no ponto F os íons estão penetrando com velocidade ![]() — usando a regra da mão esquerda no ponto F (veja figura) você verifica que sobre os íons de carga positiva a força
— usando a regra da mão esquerda no ponto F (veja figura) você verifica que sobre os íons de carga positiva a força
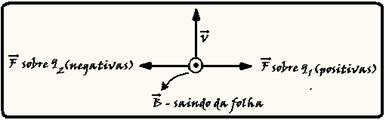
positiva a força magnética ![]() é para a direita e as cargas q1 se desviam nessa direção atingindo C1 — sobre os íons negativos essa força inverte seu sentido e as cargas q2 se desviam para a esquerda atingindo a placa C2 — essas forças magnéticas (Fm=│q│.V.B) que são responsáveis pelos desvios agem como resultantes centrípetas (Fc=mV2/R) — │q│.V.B) = mV2R — R=mV/│q│B — carga q1 — R1=m1V/│q│B (I) — carga q2 — R2=m2V/│q│B — 2R1= m2V/│q│B (II) — dividindo (I) por (II) — R1/2R1=( m1V/│q│B)/( m2V/│q│B) — m1/m2 = 1/2.
é para a direita e as cargas q1 se desviam nessa direção atingindo C1 — sobre os íons negativos essa força inverte seu sentido e as cargas q2 se desviam para a esquerda atingindo a placa C2 — essas forças magnéticas (Fm=│q│.V.B) que são responsáveis pelos desvios agem como resultantes centrípetas (Fc=mV2/R) — │q│.V.B) = mV2R — R=mV/│q│B — carga q1 — R1=m1V/│q│B (I) — carga q2 — R2=m2V/│q│B — 2R1= m2V/│q│B (II) — dividindo (I) por (II) — R1/2R1=( m1V/│q│B)/( m2V/│q│B) — m1/m2 = 1/2.
Força magnética sobre um condutor retilíneo imerso num campo magnético
18- A intensidade da força magnética sobre um fio percorrido por corrente elétrica é fornecida por:
![]()
Fm – intensidade da força magnética que age sobre o fio – medida em newton (N), no SI.
B – intensidade do campo magnético – medido em tesla (T), no SI.
i – corrente elétrica no fio – medida em ampère (A), no SI.
θ – ângulo entre a direção de B e de i.
A direção e sentido de ![]() é fornecida pela regra da mão esquerda (veja figura) onde o dedo médio indica o sentido da
é fornecida pela regra da mão esquerda (veja figura) onde o dedo médio indica o sentido da
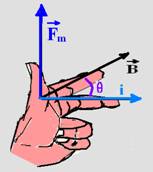
Dados — ℓ=0,2m — i=2A — b=0,09t — θ=30o — Fm=B.i.ℓ.senθ=0,09x2x0,02×0,5 — Fm=0,018N —R- A.
19- Um dos processos práticos para se determinar a direção e o sentido do vetor indução magnética ![]() ou vetor campo magnético
ou vetor campo magnético![]() , é a regra da mão direita. Esse sentido de
, é a regra da mão direita. Esse sentido de![]() depende do sentido da corrente que o origina.
depende do sentido da corrente que o origina.
Você coloca o polegar no sentido da corrente com a mão espalmada (primeira figura), em seguida
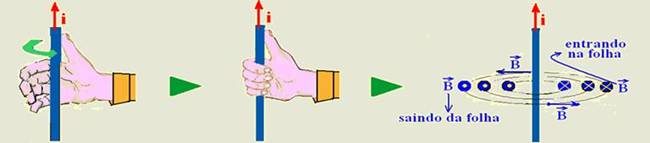
você fecha a mão como se fosse pegar o fio (segunda figura) e o sentido da “fechada” de mão é o sentido do vetor![]() (terceira figura). Observe na terceira figura que
(terceira figura). Observe na terceira figura que ![]() é sempre tangente às linhas de indução em cada ponto.
é sempre tangente às linhas de indução em cada ponto.
O polo norte de uma bússola indica sempre o sentido das linhas de indução fornecido pela regra da mão direita — observe nas figuras abaixo que, pelo enunciado do exercício, você está observando a figura (II) que é a figura (I) vista

de cima — R- A.
Campo magnético originado por um condutor retilíneo extenso – Força de interação entre dois fios condutores paralelos
39– Se você não domina a teoria, ela está a seguir:
Considere um condutor retilíneo de comprimento ℓ percorrido por uma corrente elétrica (elétrons livres com carga q, movendo-se com velocidade![]() no interior do condutor, pela sua seção transversal). Esse fio condutor reto está imerso num campo magnético uniforme
no interior do condutor, pela sua seção transversal). Esse fio condutor reto está imerso num campo magnético uniforme ![]() . Sobre cada
. Sobre cada
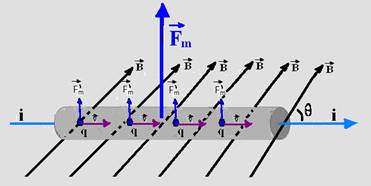
carga elétrica q que constituem a corrente elétrica i surge uma força magnética fornecida pela expressão Fm’=q.V.B.senθ e somando as intensidades de cada força Fm’ obtém-se uma força resultante Fm=n.Fm’, onde n é o número de cargas que passam pelo fio condutor num intervalo de tempo Δt — Fm=n.q.V.B.senθ — V=ΔS/Δt=ℓ/Δt — Fm= n.q. ℓ/Δt.B.senθ — i=n.q/Δt — Fm=B.i.ℓ.senθ
![]()
Fm – intensidade da força magnética que age sobre o fio – medida em newton (N), no SI.
B – intensidade do campo magnético – medido em tesla (T), no SI.
i – corrente elétrica no fio – medida em ampère (A), no SI.
θ – ângulo entre a direção de B e de i.
![]() A direção e sentido de
A direção e sentido de ![]() é fornecida pela regra da mão esquerda (veja figura abaixo) onde o dedo médio indica o
é fornecida pela regra da mão esquerda (veja figura abaixo) onde o dedo médio indica o
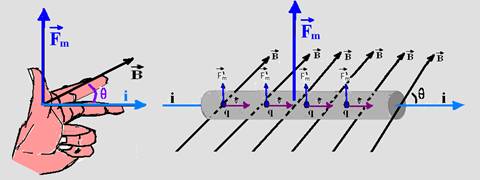
sentido da corrente elétrica i, pois o sentido convencional da corrente elétrica é o mesmo que o da velocidade das cargas positivas.
No caso do exercício a intensidade da força magnética sobre o fio vale —Fm=B.i.ℓ.sen90o=(0,50)x(i)x(1).(1) — Fm=0,5.i — peso do fio — P=m.g=15.10-3.10 — P=15.10-2N — se o fio está flutuando em repouso, então Fm=P — 0,5i=15.10-2 — i=15.10-2/0,5=30.10-2 A — i=0,30 A — para que ocorra equilíbrio a força magnética deve anular ao força peso, ou seja, ser vertical e para cima — regra da mão esquerda — polegar ![]() para cima, campo magnético
para cima, campo magnético
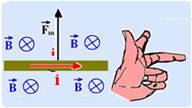
![]() entrando na folha e a corrente i deve ser para a direita — R- A.
entrando na folha e a corrente i deve ser para a direita — R- A.
40- Um dos processos práticos para se determinar a direção e o sentido do vetor indução magnética ![]() ou vetor campo magnético
ou vetor campo magnético![]() , é a regra da mão direita. Esse sentido de
, é a regra da mão direita. Esse sentido de![]() depende do sentido da corrente que o origina.
depende do sentido da corrente que o origina.
Você coloca o polegar no sentido da corrente com a mão espalmada (primeira figura), em seguida você fecha a mão

Como se fosse pegar o fio (segunda figura) e o sentido da “fechada” de mão é o sentido do vetor![]() (terceira figura). Observe na terceira figura que
(terceira figura). Observe na terceira figura que ![]() é sempre tangente às linhas de indução em cada ponto.
é sempre tangente às linhas de indução em cada ponto.
O polo norte de uma bússola indica sempre o sentido das linhas de indução fornecido pela regra da mão direita — observe nas figuras abaixo que, pelo enunciado do exercício, você está observando a figura (II) que é a figura (I) vista

de cima — R- A.
Campo magnético gerado por uma espira circular ou por um solenoide
32- a) Cálculo da carga elétrica Q que flui através dos tubos — Q=N.e=2.1014.1,6.10-19=3,2.10-5C — intervalo de tempo ∆t em que essas partículas circulam nos tubos de ∆S=27km=27.103m de perímetro com velocidade V=c=3.108m/s —
V=c=∆S/∆t — 3.108 = 27.103/∆t — ∆t=9,0.10-5s — i=Q/∆t=3,2.10-5/9.105 — i = 0,36 A.
b) A direção e o sentido do vetor indução magnética (vetor campo magnético) ![]() no interior da espira é fornecido pela
no interior da espira é fornecido pela
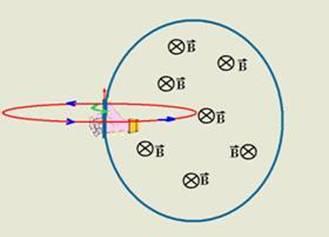
regra da mão direita (você coloca o polegar no sentido da corrente com a mão espalmada, em seguida você fecha a mão no sentido de pegar o pegar o fio e o sentido da “fechada” de mão é o sentido do vetor![]() ).
).
![]() Intensidade de
Intensidade de![]() no centro da espira circular de raio R:
no centro da espira circular de raio R:

Cálculo do raio R do (LHC) — 2πR=27.103 — R=27.103/2π=27.103/6=4,5.103m — B=1,26.10-6.0,36/4,5.103 — B=0,4536.10-6/2.4,5.103 — B=0,05.10-9 T — B=5,0.10-11 T.
33- Só existirá corrente elétrica induzida na espira se a intensidade da corrente variar, o fará com que o fluxo magnético no interior da espira produzido pela variação da corrente também varie — sendo a corrente elétrica sempre a mesma, ela não provocará uma variação de fluxo magnético no interior da espira, não surgindo corrente na mesma — R- E.
34- Sobre PN e QM não surge força magnética, pois o fio e consequentemente a corrente i é paralela ao campo magnético ![]() — em MN a força magnética
— em MN a força magnética ![]() empurra o fio para dentro da folha, portanto está penetrando nela e, em QP está puxando o fio para fora da folha, saindo dela — a direção e sentido de
empurra o fio para dentro da folha, portanto está penetrando nela e, em QP está puxando o fio para fora da folha, saindo dela — a direção e sentido de ![]() é fornecida pela regra da mão
é fornecida pela regra da mão

esquerda (veja figura) onde o dedo médio indica o sentido da corrente elétrica i — adaptando a mão esquerda você verifica que na espira a corrente i circula no sentido horário — R- E.
35– Quando uma carga elétrica que se move com velocidade ![]() no interior de um campo magnético
no interior de um campo magnético ![]() sobre ela surge uma força de origem magnética
sobre ela surge uma força de origem magnética ![]() ( denominada força de Lorentz), com as seguintes características:
( denominada força de Lorentz), com as seguintes características:
![]() Direção e sentido de
Direção e sentido de ![]() – fornecidos pela regra da mão esquerda conforme mostrado na figura
– fornecidos pela regra da mão esquerda conforme mostrado na figura

Observe na figura da direita que ![]() é perpendicular a
é perpendicular a ![]() e a
e a ![]() , o que impõe a condição de que
, o que impõe a condição de que ![]() e
e ![]() devem pertencer a um mesmo plano. Observe também que θ é o ângulo entre
devem pertencer a um mesmo plano. Observe também que θ é o ângulo entre ![]() e
e ![]() .
.
![]() Intensidade de
Intensidade de ![]() – é proporcional a q, V, B e ao senθ, obedecendo à equação:
– é proporcional a q, V, B e ao senθ, obedecendo à equação:

Como a força magnética tem sempre direção perpendicular ao vetor velocidade (regra da mão esquerda) e como a potência de uma força é fornecida por Po=Fm.V.cosθ, então θ=90o e cos 90o=0 — Po=Fm.V.0 — Po=0 — se a potência é nula o trabalho também será — W=0 — o trabalho realizado pela força magnética é sempre nulo ou, a força magnética nunca realiza trabalho — se o trabalho é nulo, a energia cinética é constante e , portanto, a velocidade também é, o que está representado no gráfico do item (a) — R- A,
20- A energia máxima com que um elétron pode ser emitido é toda energia cinética disponível que, por sua vez, é a energia máxima de um fóton dada por — E=h.fmax=h.c/λmax — λmax=h,c/E=4,1.10-15.3.108/4.104≈3,07.10-11m x 1010=0,307![]() .
.
R- A.
Fluxo magnético- Indução eletromagnética – Sentido da corrente elétrica induzida
37- A lei de Lenz se refere ao sentido da corrente elétrica induzida afirmando que a corrente elétrica induzida, sempre tem sentido oposto as linhas do campo magnético indutor: “ O sentido da corrente elétrica induzida é tal que, por seus efeitos, opõe-se à causa que lhe deu origem” — é corrente alterna pois, quando o imã se aproxima a corrente elétrica é num sentido e, quando se afasta, no outro sentido — R- B.
38- Gráfico da corrente elétrica induzida – considere uma espira de qualquer formato ou uma bobina (solenoide) girando com velocidade angular W no interior de um campo magnético uniforme. A corrente elétrica induzida é uma função senoidal do tempo e é alternada porque ela percorre a espira ou bobina invertendo seu sentido durante um ciclo, como indica o gráfico i X t.
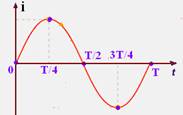
Observe as seqüências abaixo onde a espira inicia seu giro no sentido horário: A corrente i inicia seu ciclo quando t=0, aumenta

até atingir um valor máximo em t=T/4; diminui até se anular em t=T/2: inverte seu sentido e aumenta até atingir um valor máximo em módulo (mínimo) em t=3T/4 e em seguida diminui até chegar novamente a zero, quando reinicia um novo ciclo.
R- A.
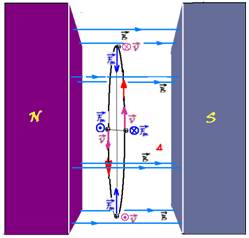
39– Considere um elétron situado a uma distância R do eixo de rotação com o disco metálico girando com velocidade angular (W) constante no sentido indicado — se a velocidade angular W é constante, a velocidade linear (tangencial) V também será constante, pois W=V.R — a figura mostra
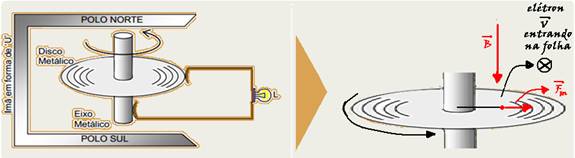
um corte vertical na folha de papel e, observe que o elétron está perpendicular ao plano do papel e penetrando nele — utilizando a regra da mão esquerda surgirá sobre o elétron uma força magnética Fm impulsionando-o para a direta com velocidade V constante, pois W é constante — essa força magnética tem intensidade Fm=q.V.B.cos90o=q.V.B — e é constante, pois q, V e B tem intensidades constantes — assim, a média a média dessas forças sobre todos os elétrons livres também é constante, mantendo uma força-eletromotriz (ddp) induzida constante ε entre o centro e a periferia do disco que não varia com o tempo — se R=U/i ou R=ε/i e, como R e ε são constante, a corrente i também será constante — a potência elétrica P=R.i2 será constante, pois R e i são constantes — o gráfico que indica potência constante é o da alternativa D.
R- D.
40- Todos os fenômenos mencionados na explicação acima, do funcionamento do trem MAGLEV estão baseados no fenômeno da indução eletromagnética baseada na lei de Faraday-Lenz — R- D.
41-
1. Veja a teoria a seguir:
![]() Um dos processos práticos para se determinar a direção e o sentido do vetor indução magnética
Um dos processos práticos para se determinar a direção e o sentido do vetor indução magnética ![]() ou vetor campo magnético
ou vetor campo magnético![]() , é a regra da mão direita. Esse sentido de
, é a regra da mão direita. Esse sentido de![]() depende do sentido da corrente que o origina.
depende do sentido da corrente que o origina.
Você coloca o polegar no sentido da corrente com a mão espalmada (primeira figura), em seguida você fecha a mão

para pegar o fio (segunda figura) e o sentido da “fechada” de mão é o sentido do vetor![]() (terceira figura). Observe na terceira figura que
(terceira figura). Observe na terceira figura que ![]() é sempre tangente às linhas de indução em cada ponto.
é sempre tangente às linhas de indução em cada ponto.
Define-se fluxo magnético pela letra Φ (fi), como sendo o produto entre o vetor indução magnética![]() , a área S da espira e o cosseno do ângulo α formado entre
, a área S da espira e o cosseno do ângulo α formado entre ![]() e
e ![]() , ou seja:
, ou seja:

![]() Observe que o fluxo magnético Φ pode ser considerado como a grandeza física que mede o número de linhas de indução que atravessam a superfície de uma espira e que o fluxo será máximo
Observe que o fluxo magnético Φ pode ser considerado como a grandeza física que mede o número de linhas de indução que atravessam a superfície de uma espira e que o fluxo será máximo 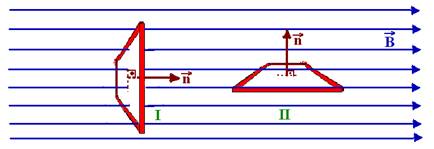
quando α=0o (número de linhas de indução que atravessam a espira é máximo – I) e será nulo quando α=90o (nenhuma linha de indução atravessa a espira – II), o que é o caso do exercício, não surgindo nenhuma corrente elétrica induzida na espira — R- Não.
2. Veja na figura que, nesse caso, as linhas de indução do campo magnético criado pela corrente elétrica estão saindo
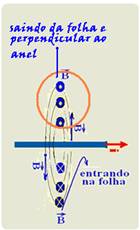
do interior do anel, perpendiculares a ele, gerando um fluxo magnético no interior do mesmo — esse fluxo magnético é variável pois a corrente elétrica no fio também o é, o que fará surgir uma corrente elétrica induzida no anel, de acordo com a lei de Faraday-Newman — Sim.
3. Veja na figura que na parte superior do anel existe um fluxo de indução magnética variando num sentido (linhas de
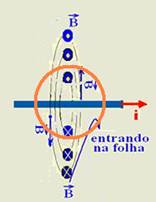
campo saindo) e na parte inferior em outro sentido (linhas de campo entrando) — esse fenômeno gera nessas duas partes, superior e inferior do anel) forças eletromotrizes induzidas de polaridades opostas, que se anulam — assim não haverá corrente elétrica induzida na espira — não.
Força eletromotriz induzida
Transformadores
58– (V) – O fenômeno da indução eletromagnética foi descoberto por Faraday em 1831, quando observou que um campo magnético pode induzir um campo elétrico, ou seja, demonstrou que, aproximando e afastando um imã de uma espira de fio condutor conectada a um galvanômetro (dispositivo que indica pequenas correntes), durante o movimento do imã o galvanômetro detectava o aparecimento de uma corrente elétrica no fio, e quando o imã parava, essa corrente elétrica cessava.
![]() A partir do fenômeno da indução eletromagnética foram construídos geradores de energia elétrica através das usinas
A partir do fenômeno da indução eletromagnética foram construídos geradores de energia elétrica através das usinas



hidrelétricas, termoelétricas ou nucleares que giram turbinas as quais movem gigantescos imãs e bobinas.
(F) – A lei de Lenz se refere ao sentido da corrente elétrica induzida afirmando que a corrente elétrica induzida, sempre tem sentido oposto as linhas do campo magnético indutor: “ O sentido da corrente elétrica induzida é tal que, por seus efeitos, opõe-se à causa que lhe deu origem”
(V) – A função de um transformador é aumentar ou diminuir a diferença de potencial voltagem). Trata-se de um


dispositivo de corrente alternada que opera baseado nos princípios eletromagnéticos da Lei de Faraday e da Lei de Lenz.
(V) – Michael Faraday, experimentalmente observou que a tensão média induzida e consequentemente a corrente elétrica induzida é maior quanto mais rápida for a variação do fluxo magnético no circuito. Lembrando que a essa tensão média induzida dá-se o nome de força eletromotriz induzida. Assim, ele definiu essa lei da seguinte maneira:
“ O módulo da força eletromotriz induzida num circuito é igual à razão entre a variação do fluxo magnético nesse circuito, pelo intervalo de tempo em que essa variação ocorre”

Eventualmente, devido à lei de Lenz, que afirma que a força eletromotriz induzida se opõe à variação de fluxo, costuma-se escrever a lei de Lenz da seguinte forma:
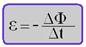
Define-se fluxo magnético pela letra Φ (fi), como sendo o produto entre o vetor indução magnética![]() , a área S da espira e o cosseno do ângulo α formado entre
, a área S da espira e o cosseno do ângulo α formado entre ![]() e
e ![]() , ou seja:
, ou seja:

Observe que em nenhuma das expressões acima surge a resistência elétrica R.
R- 2.
59–
1. Veja a teoria a seguir:
![]() Um dos processos práticos para se determinar a direção e o sentido do vetor indução magnética
Um dos processos práticos para se determinar a direção e o sentido do vetor indução magnética ![]() ou vetor campo magnético
ou vetor campo magnético![]() , é a regra da mão direita. Esse sentido de
, é a regra da mão direita. Esse sentido de![]() depende do sentido da corrente que o origina.
depende do sentido da corrente que o origina.
Você coloca o polegar no sentido da corrente com a mão espalmada (primeira figura), em seguida você fecha a mão

para pegar o fio (segunda figura) e o sentido da “fechada” de mão é o sentido do vetor![]() (terceira figura). Observe na terceira figura que
(terceira figura). Observe na terceira figura que ![]() é sempre tangente às linhas de indução em cada ponto.
é sempre tangente às linhas de indução em cada ponto.
Define-se fluxo magnético pela letra Φ (fi), como sendo o produto entre o vetor indução magnética![]() , a área S da espira e o cosseno do ângulo α formado entre
, a área S da espira e o cosseno do ângulo α formado entre ![]() e
e ![]() , ou seja:
, ou seja:

![]() Observe que o fluxo magnético Φ pode ser considerado como a grandeza física que mede o número de linhas de indução que atravessam a superfície de uma espira e que o fluxo será máximo quando α=0o (número de linhas de
Observe que o fluxo magnético Φ pode ser considerado como a grandeza física que mede o número de linhas de indução que atravessam a superfície de uma espira e que o fluxo será máximo quando α=0o (número de linhas de

indução que atravessam a espira é máximo – I) e será nulo quando α=90o (nenhuma linha de indução atravessa a espira – II), o que é o caso do exercício, não surgindo nenhuma corrente elétrica induzida na espira — R- Não.
2. Veja na figura que, nesse caso, as linhas de indução do campo magnético criado pela corrente

elétrica estão saindo do interior do anel, perpendiculares a ele, gerando um fluxo magnético no interior do mesmo — esse fluxo magnético é variável pois a corrente elétrica no fio também o é, o que fará surgir uma corrente elétrica induzida no anel, de acordo com a lei de Faraday-Newman — Sim.
3. Veja na figura que na parte superior do anel existe um fluxo de indução magnética variando num

sentido (linhas de campo saindo) e na parte inferior em outro sentido (linhas de campo entrando) — esse fenômeno gera nessas duas partes, superior e inferior do anel) forças eletromotrizes induzidas de polaridades opostas, que se anulam — assim não haverá corrente elétrica induzida
