Resolução comentada das questões de Física – vestibulares recentes – Eletrodinâmica – 2018/2019

01-

02-

03-

Cálculo da potência da bateria Po = i.U = 2.5 Po = 10 W.

A energia W utilizada no processo do carregamento foi de 90% de 105 j = 0,9.105 W = 9.104 J.

Po = W/t 10 = 9.104/t t = 9.104 /10 t = 9.103 = 9000s/3,6 = 2,5 h.

R- B

04-

Toda bateria possui um polo positivo e um polo negativo, características semelhantes às desse peixe, onde o polo positivo seria a cabeça e o negativo a cauda.

Esses dois polos originam uma diferença de potencial (tensão ou voltagem) que originam a movimentação de corrente elétrica, que no caso do peixe, quando tocado, pode liberar uma forte descarga elétrica, imobilizando e até matando suas presas ou agressores.

R- C

05-

R- A

06-

Se você não domina a teoria, ela está a seguir:

Se você dobrar o valor da resistência a potência ficará 2 vezes menor e se você triplicar a ddp a potência ficará 32 = 9 vezes maior P’ = 9P/2.

R- E

07-

São dados: P = 5,5.103 W; U = 220 V e i = ?

P = i.U 5,5.103 = i.220 i = 5500/220 i = 25 A.

R- D

08-

Veja na tabela que a energia total consumida em 1 mês (30 dias) foi de Wt = 375 kWh e como a chaleira consome 2% dessa energia em 30 dias ela consumirá W1 = 0,02×375 W1 = 7,5 kWh (em 30 dias).

Em 1 dia ela consumirá W2 = 7,5/30 W2 = 0,25 kWh (energia gasta pela chaleira em 1 dia).

Mas o tempo de funcionamento dela por dia é t = 15 min = 15/60 = 1/4 = 0,25 h.

Po = W2/t = 0,25/0,25 Po = 1 kW = 1000 W

R- C

09-

Chuveiro t = 30 diasx20/60h = 10 h P = 7000 W = 7 kW energia W = P.t = 7.10

W = 70 kWh preço C$ = 70×0,5 C$ = 35,00

Lâmpada t = 24×30 = 720 h P = 100 W = 0,1 kW energia W = P.t = 0,1.720

W = 72 kWh preço C$ = 72×0,5 C$ = 36,00

R- A

10-

Veja o resumo teórico abaixo:

R – C

11-

R- C

12-

Nas condições da figura A, a ddp U do gerador deve ser a mesma que a do resistor e na figura B é o ponto onde a reta e a curva se interceptam ou seja, quando U = 10 V, i = 0,14 A.

P = i.U = 0,14.10 P = 1,4 W,

R- D

13-

R- E

14-

Fórmulas – Lei de Ohm

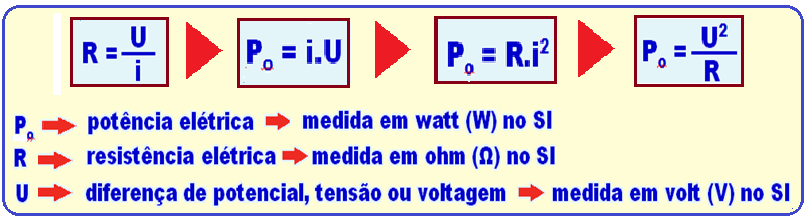
R = 22 Ω U = 220 V R = 22 = i = i = 10 A

R- C

15-

Fórmulas – Lei de Ohm

São dados: U = 20 V, P = 300 W e t = 1 min = 60 s.

P = i.U 300 = i.20 i = 300/20 = 15 A.

Energia = potênciaxtempo W = 300×60 = 18000 J

R- E

16-

17-

Lâmpada fluorescente

Cálculo do custo total de uma lâmpada fluorescente de potência Pf = 28 W = 28.10-3 kW durante sua vida útil fornecida (tf = 10000 h = 104 h).

Energia elétrica (Wf) consumida por essa lâmpada durante sua vida útil Wf = Pf.tf = 28.10-3 kW. 104h Wf = 280 kWh.

Custo total de cada lâmpada fluorescente C$ = 70,00 + preço de uma lâmpada = 70,00 + 20,00 C$ = 90,00.

Lâmpada incandescente

Cálculo do custo total de uma lâmpada incandescente de potência Pf = 100 W = 10-1 kW durante a mesma vida útil que a da fluorescente (tf = 10 000 h = 104 h).

Energia elétrica (Wf) consumida por essa lâmpada durante sua vida útil Wf = Pf.tf = 10-1 kW. 104h Wf = 103 kWh = 1 000 kWh.

Observe que você necessita de 10 lâmpadas incandescentes (vida útil 10 000 h) para operar na mesma vida útil (mesmo período de tempo) que a das fluorescentes (vida útil 1 000 h).

Assim, o custo total de cada incandescente deverá ser C$ = custo de uma incandescente + 10xpreço de uma lâmpada incandescente = 250,00 + 10×4,00 C$ = 290,00 (custo total de cada incandescente para a mesma vida útil de cada fluorescente)

Assim, o valor poupado será C$ = 290,00 – 90,00 = 200,00.

R- C

18-

Antes da troca energia consumida pelas duas lâmpadas fluorescentes de 20 W cada acesas durante ∆t = 4 h por noite W1 = 2.P. ∆t = 2.20.4 = 160 Wh + dispositivos de 200 W ligados por 4 h = 800 Wh.

Wantes = 160 + 800 Wantes = 960 Wh.

Depois da troca energia consumida pela duas lâmpadas de LED de 9 W cada acesas durante ∆t = 6 h por noite W2 = 2.P. ∆t = 2.9.6 = 108 Wh + dispositivos de 200 W ligados por 5 h = 1000 Wh.

Wdepois = 108 + 1000 Wdepois = 1108 Wh.

Diferença W’ = Wdepois – Wantes = 1108 – 960 W’ = 148 Wh.

R- A

19-

Como é pedida a maior potência elétrica você deve selecionar a maior corrente elétrica fornecida pelo gráfico, que é de imáx = 60 A e, se a tensão é constante U = 110 V, basta você utilizar a expressão Pmáx = imáx.U = 60.110 Pmáx = 6600 W = 6,6 kW.

R- D

20-

Para esse exercício nem é necessário utilizar conhecimentos de física, visto que a potência não muda, o importante mesmo é o tempo utilizado. Em 6 dias por semana por 30 min (meia hora) nós temos:

6.0,5 horas = 3 horas

No outro caso se utiliza o ferro 2 horas por semana. Então se economiza 3 – 2 = 1 hora por semana. Se fizermos a divisão 1/3 = 0,33 = 33% temos o quanto economizamos por semana em relação ao valor inicial. Alternativa B

21-

Energia elétrica W consumida por cada aparelho, por dia:

Geladeira Wg = Pg. Wg = 0,25. = 6,0 kWh.

Computador Wc = Pc. Wc = 0,50. = 1,0 kWh.

Televisão Wt = Pt. Wt = 0,10. = 0,5 Wh .

Ar condicionado Wa = Pa. Wg = 3,00. = 15 kWh.

Chuveiro Wc = Pc. Wc = 4,00. = 2,0 kWh.

Forno Wf = Pf. Wf = 1,50.1/3 = 0,5 kWh.

Energia total consumida por dia Wt = 25 kWh

Como cada painel de 1,0 m2 de área gera, em média, 0,5 kWh por dia, o número mínimo de painéis será 25/0,5 = 50 painéis.

R – C

22-

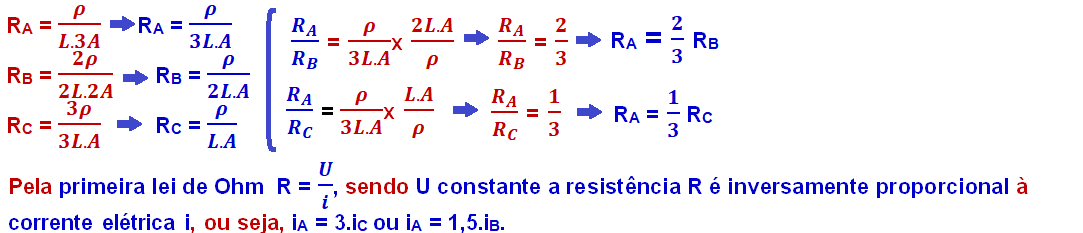
Segunda lei de Ohm (resistividade)

01. Correto – a expressão R = l/A indica que a resistência elétrica R é diretamente proporcional ao comprimento l do fio.

02. Correto – a expressão R = l/A indica que a resistência elétrica R é inversamente proporcional a área A da seção transversal de um resistor. Assim, quanto maior for a área A da seção transversal de um resistor, menor será sua resistência elétrica.

04. Correto – se associados em série você terá apenas um resistor de resistência 2R e a resistência oferecida por apenas um desses resistores com as mesmas características, mas com o dobro do comprimento l também será 2R, pois resistência elétrica R é diretamente proporcional ao comprimento l do fio.

08. Correto – se associados em paralelo você terá apenas um resistor de resistência R/2 e a resistência oferecida por apenas um desses resistores com as mesmas características, mas com o dobro da área de seção transversal também será R/2, pois resistência elétrica R é inversamente proporcional à área de seção transversal A do fio.

16- Falso – Dedução da unidade da resistividade (ρ) no sistema internacional de unidades (SI)

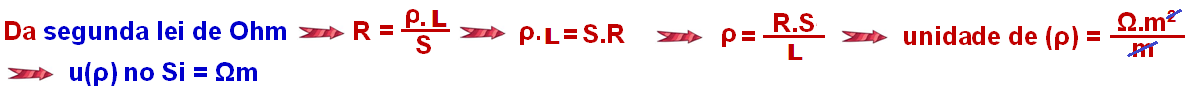
R- (01 + 02 + 04 + 08) = 15

23-

Efeito Joule

Efeito Joule num condutor metálico, os elétrons livres da corrente elétrica, durante suas movimentações, sofrem continuamente colisões com os átomos da rede cristalina desse condutor, transferindo a eles parte de sua energia cinética e, como resultado, os átomos do condutor, como um todo, passam a vibrar com uma energia maior.

Esse aumento do “nível de vibração” dos átomos do condutor provocam um aumento de sua temperatura, fazendo-o liberar energia térmica (calor). Esse fenômeno é denominado efeito Joule.

Sendo a potência da P da fonte (usina geradora) constante, pela expressão P = i.U, quanto maior a tensão U no gerador, menor será a corrente (menor perda por efeito Joule) na linha capaz de transmitir uma determinada potência ao consumidor.

Essa perda de potência P (e consequentemente de energia elétrica) por efeito Joule é fornecida pela expressão P = R.i2 onde P é a potência da fonte constante, R a resistência equivalente da linha de transmissão e i a intensidade da corrente elétrica na mesma. Assim, como convém P dissipada menor, você deve diminuir R e i.

Para diminuir a resistência equivalente R da linha de transmissão, pela segunda lei de Ohm

fornecida acima, mantendo L e S constantes, você deve diminuir o valor da resistividade (R e são diretamente proporcionais)

R- D

24-

Segunda lei de Ohm

25-

São dados: ρ = 2,8.10–8 Ω; L = 1000 m = 103 m; A = 2 mm2 = 2.10-6 m2.

R = ρ.L/A = 2,8.10-8.103/2.10-6 = 1,4.10-5/10-6 = 1,4.10 R = 14 Ω

R- D

26-

Primeira lei de Ohm

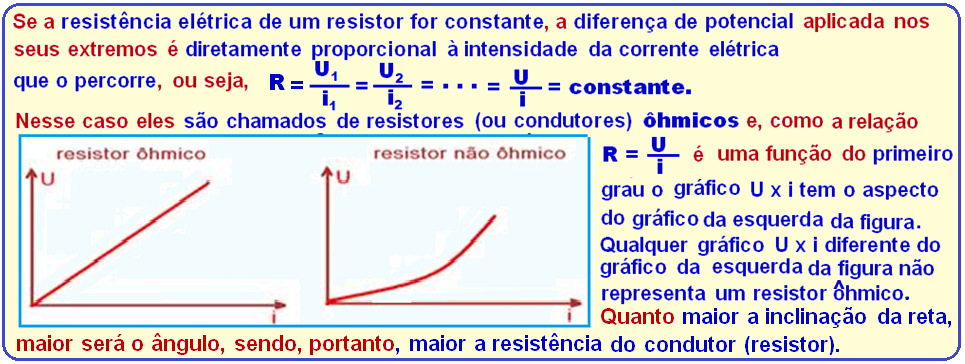
Segunda lei de Ohm (Resistividade)

O gráfico Vxi fornecido refere-se à primeira lei de Ohm (teoria acima) onde R é constante para quaisquer valores de V e i e, por exemplo, escolhendo quando V = 50 V, i = 100 mA = 100.10-3 A = 0,1 A R = v/i R = 50/0,1 R = 500 Ω.

Aplicando agora a 2a lei de Ohm (veja teoria acima) sendo dados: R = 500 Ω; L = 2 m e 1,75. 10-6 .m R = /S 500 = 1,75.10-6.2/S 500S = 3,5.10-6 S = 3,5.10-6/5.102 = 0,7.10-8 m2 = 0,7.

10-8.104 S = 0,7.10-4 cm2.

R- B

27-

Como tem curto circuito vamos refazer a associação marcando todos os nós que possuem o mesmo potencial com a mesma letra (A) e os outros, C e D e, em seguida vamos calcular a resistência do resistor equivalente conforme a sequência a seguir:

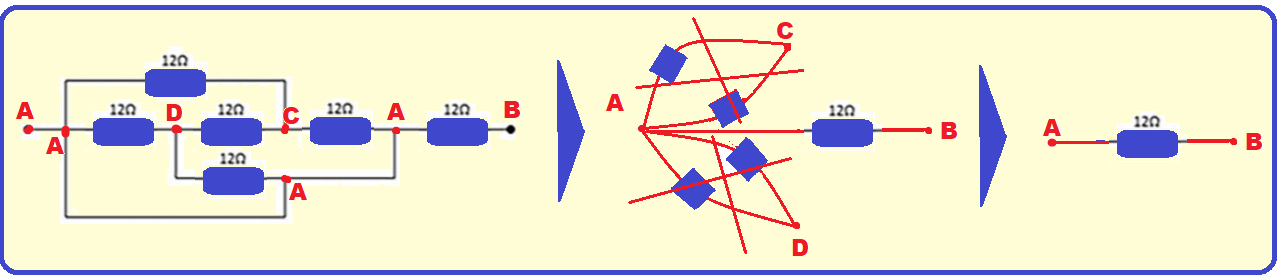
Entre os pontos A e B a corrente circula apenas pelo ultimo resistor de 12 Ω Req = 12

Ou ainda, veja na figura que se a corrente elétrica i entrar pelo ponto A ela se desviará conforme

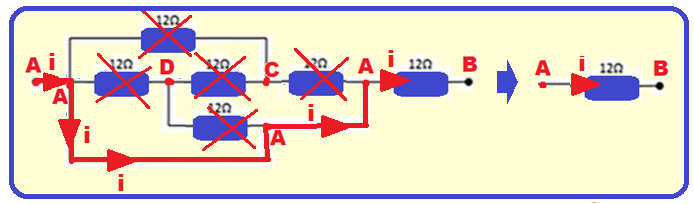
Indicado e circulará apenas pelo último resistor Req = 12

R- B

28-

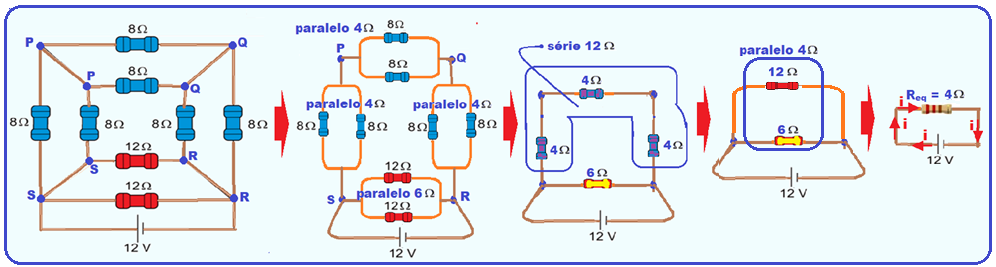
Observe que os pontos P,Q, R e S possuem o mesmo potencial (curto circuito) então você pode uni-los (primeira e segunda figuras) refazendo o circuito e, calculando a resistência do resistor equivalente conforme a sequência de figuras.

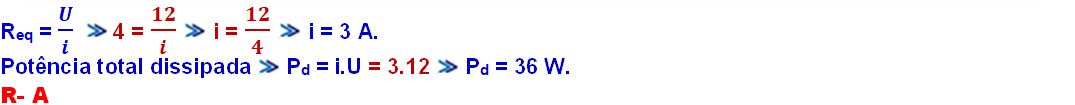
29-

Formulas utilizadas na resolução do exercício:

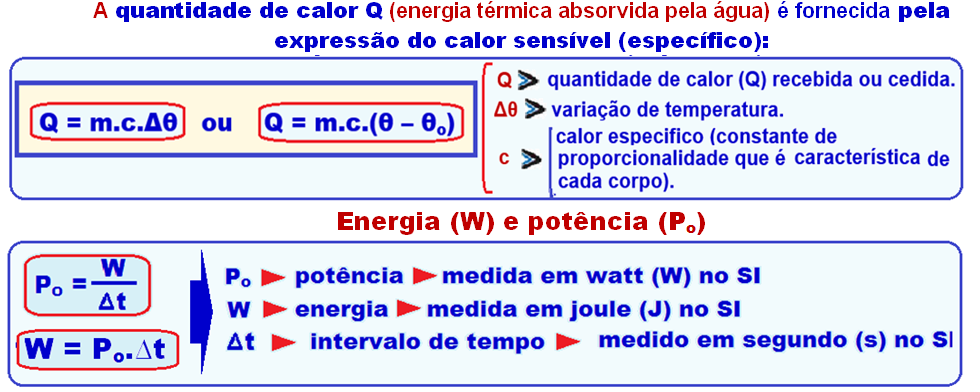
Relações entre corrente elétrica (i), tensão (U), resistência elétrica (R) e

potencia elétrica (Po)

Resolução do exercício

30-

Todos os dados já estão no SI. É possível notar que há uma chave aberta e uma chave fechada no circuito. O ramo que está com a chave aberta não permite a passagem de corrente e, portanto, pode ser desconsiderado junto com a resistência que há nele, pois o circuito não o ‘sente’. Assim, a resistência equivalente será a operação entre as duas resistências em paralelo:

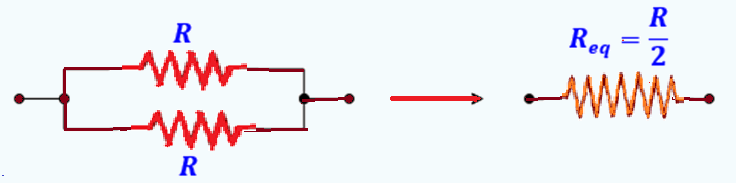
A resistência equivalente é a resistência que produz os mesmos efeitos de corrente e tensão quando substitui as duas outras resistências no circuito, com isso e com a lei de Ohm é possível calcular a corrente que flui pelo circuito, a lei de Ohm é dada por:

Onde U é a tensão imposta no resistor e I é a corrente que passa por ele. Usando essa lei chegamos a:

31-

Como as três pilhas estão associadas em paralelo (mesma ddp) elas se comportam como se fossem uma única pilha de ddp U = 25 V.

Observe com atenção os resistores e veja que R1 está em série com R2 e R3 que estão em paralelo entre si e que o voltímetro está indicando apenas a ddp dessa associação paralelo.

Veja um esquema simbólico dessa associação e na sequência das figuras o cálculo da resistência do resistor equivalente Req e da corrente elétrica total i.

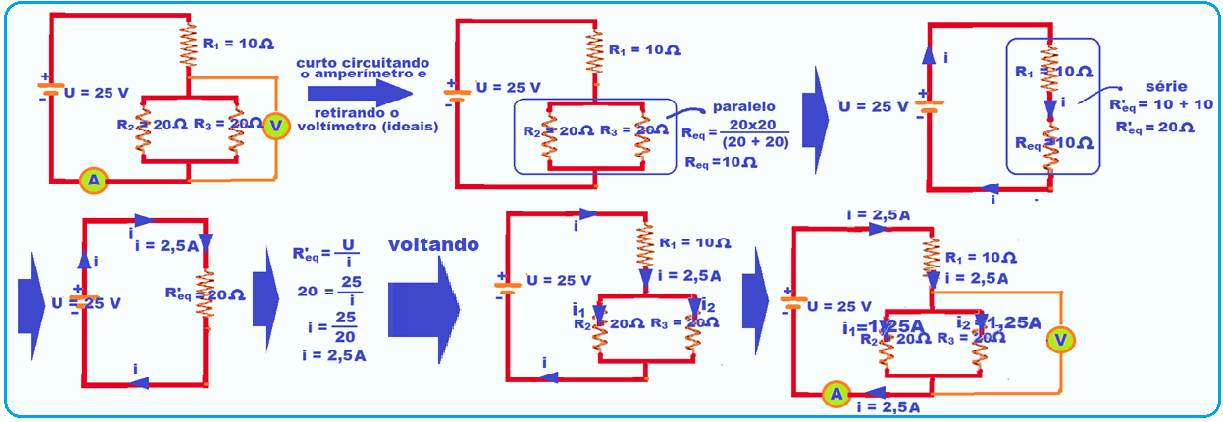
Quando a corrente total i = 2,5 A chega na associação paralelo de resistores de mesmo valor (10 Ω) ela se divide pela metade e cada resistor fica percorrido por i = 1,25 A e sob ddp de U = R.i = 10.1,25 = 12,5 V, que é a indicação do voltímetro colocado em paralelo em seus terminais.

O amperímetro indica a corrente que passa por ele que vale i = 2,5 A.

R- D

32-

Se as lâmpadas são idênticas cada uma possui a mesma resistência elétrica RL e são percorridas pela mesma corrente iL.

Observe no esquema do circuito que, se o resistor R está sob ddp de U = 3V, cada uma das três lâmpadas terão a mesma ddp (paralelo a ddp é a mesma) de U’ = (12 – 3) = 9 V.

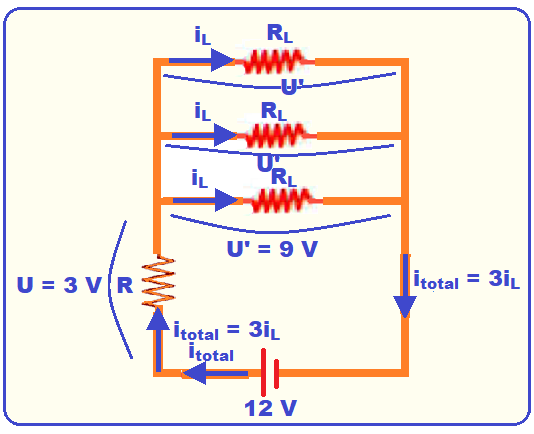
Como cada lâmpada está sob ddp de U’ = 9 V pelo gráfico você verifica que a corrente em cada lâmpada será iL = 100 mA = 100.10-3 A = 0,1 A. Assim, a corrente total será itotal = 3iL = 3.0,1= 0,3 A.

Essa corrente itotal = 0,3 A é a corrente que passa pelo resistor R que está sob ddp de U = 3V.

R- A

33-

Se você aumenta a resistência variável R mantendo U constante você estará diminuindo i, pois na expressão R =U/i, com U constante R e i são inversamente proporcionais.

Se você diminui P você estará diminuindo i, pois na expressão P = U.i, com U constante, P e i são i são diretamente proporcionais e, ao mesmo tempo estará diminuindo a energia consumida E pois,

P = E/t, com t constante P e E são diretamente proporcionais.

R- A

34-

Na associação paralelo a resistência do resistor equivalente pode ser calculada por Req = produto/soma = (40 x 10)/(40 + 10) = 400/50 Req = 8 Ω.

Na associação paralelo a tensão U = 12 V é a mesma para os dois resistores P40Ω = U2/R = 122/40 =

144/40 P40Ω = 3,6 W Req = U/i 8 = 12/i i = 1,5 A

R- C

35-

Falsa a potência é função do valor da resistência elétrica e, como a corrente i é a mesma, para uma lâmpada a potência será P1 = R.i2 e para as três P3 = 3Ri2. P3 > P1.

B. Falsa veja (A).

C. Falsa nas instalações residenciais a associação utilizada é a paralelo (mesma tensão, ddp ou voltagem U).

D. Falsa uma das características da associação série é de que a corrente i é a mesma.

E. Correta;

R- E

36-

Observe que a resistência variável Req e o ferro elétrico de resistência RF estão associados em série

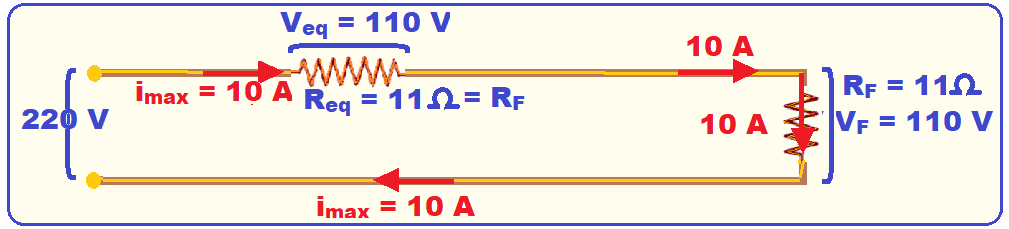
Sendo a corrente máxima i = 10 A a mesma para os dois (característica da associação série) e como a tensão no ferro deve ser de VF = 110 V, a tensão em Req também deve ser de Veq = 110 V, pois Ventrada = 220 V deve ser a soma das tensões parciais ou seja, a tensão em cada um deve ser de 110 V (característica da associação série).

R – B

37-

A figura abaixo mostra um desses isolantes topológicos e, observe que a tensão U é a mesma

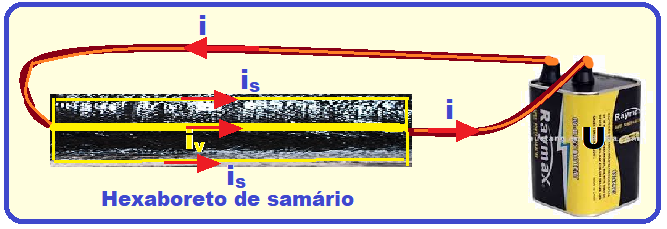
para cada resistência (da superfície e do interior) e que elas estão associadas em paralelo.

Características da associação paralelo

Os resistores são associados pelos seus terminais, ou seja, todos saem de um mesmo ponto e todos chegam a um mesmo ponto.

A diferença de potencial (tensão) U de toda a associação (entre A e B) é a mesma para todos os resistores

A corrente total i é a soma das correntes parciais, ou seja, i = i1 + i2 + i3

Fórmulas válidas para a associação paralelo

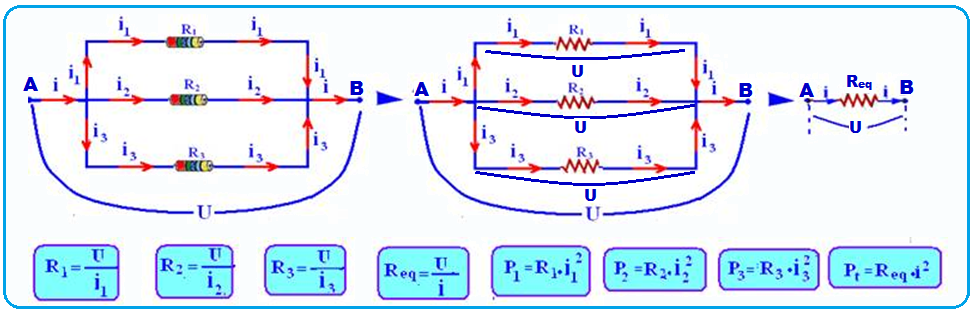
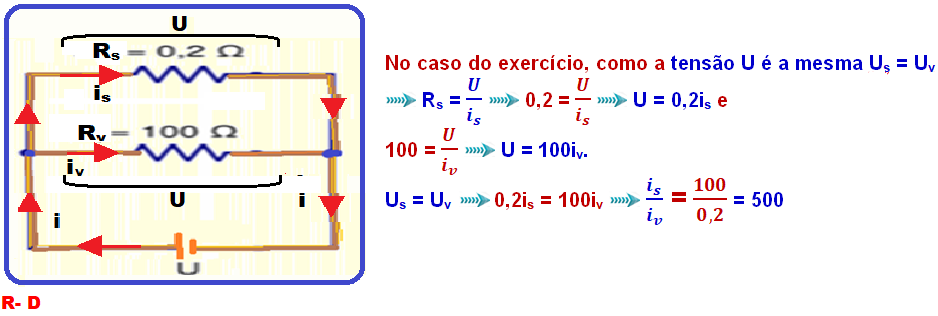
38-

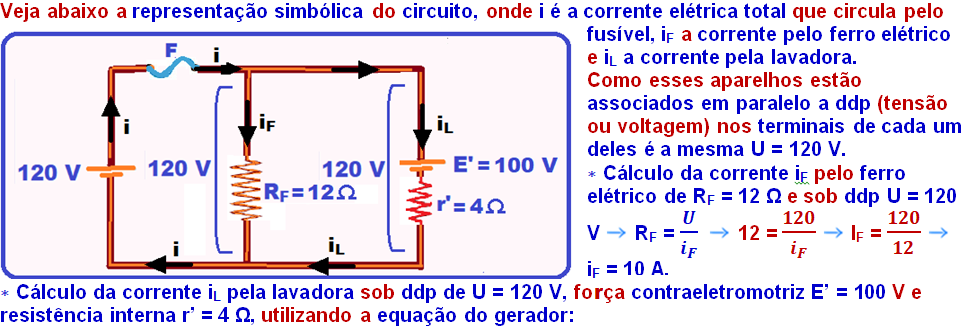
a) Claro que os aparelhos mencionados estão associados em paralelo, pois a ddp (tensão, voltagem) é a mesma para todos (U = 110 V).

Associação paralelo

39-

1. Correta Uma associação série é aquela em que os resistores estão associados um em seguida do outro de modo que a corrente em cada um seja a mesma.

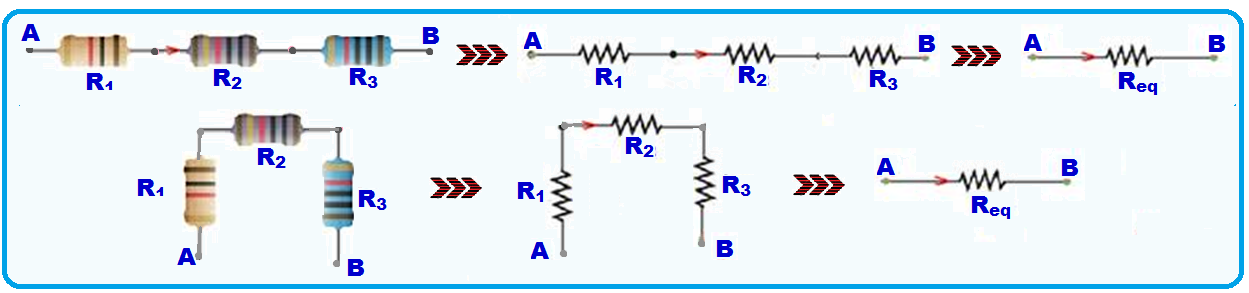
Cálculo da resistência (Req) do resistor equivalente na associação série a resistência do resistor equivalente entre A e B é fornecida pela soma das resistências de cada resistor.

Portanto, numa associação de resistores em série, o resistor equivalente sempre tem resistência maior que qualquer uma das resistências dos resistores que formam a associação.

02. Falsa A tensão U é a mesma para todos os capacitores. Veja informação abaixo:

03. Correta Veja as informações abaixo:

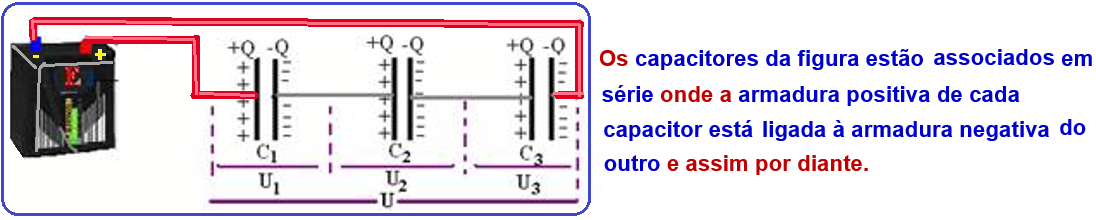
No processo de carga, quando os capacitores em série estiverem ligados ao gerador de tensão U, as cargas que saem de uma armadura serão deslocadas para a seguinte até que as cargas de todas as armaduras tenham o mesmo módulo, ou seja, Q1 = Q2 = Q3 = Q, que é igual à carga do capacitor equivalente.

Observe que, se as cargas são iguais e as capacitâncias são diferentes, a diferença de potencial (tensão) também será diferente.

Você também pode calcular o capacitor equivalente como Ceq = produto/soma tomados dois a dois.

Lembre-se de que o Ceq é sempre menor que a capacitância de cada um dos capacitores associados.

R- E

40-

Formulas utilizadas na resolução do exercício:

Relações entre corrente elétrica (i), tensão (U), resistência elétrica (R) e

potencia elétrica (Po)

Resolução do exercício

41-

Onde U é a tensão imposta no resistor e I é a corrente que passa por ele. Usando essa lei chegamos a:

42-

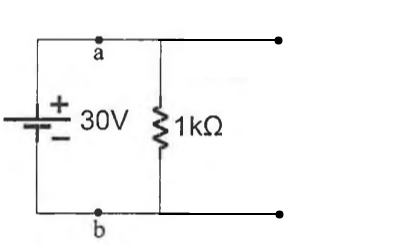
A ideia principal nesse problema é lembrar que o capacitor funciona como um circuito aberto em corrente contínua, assim não haverá passagem de corrente na malha em que o capacitor se encontra, inutilizando o resistor que se encontra ali. A corrente I que flui pelo circuito é então apenas a que passa na malha em que se encontra a fonte U=30 V e a resistência restante R, o circuito equivalente com essas modificações é exibido na imagem abaixo.

43-

Como as três pilhas estão associadas em paralelo (mesma ddp) elas se comportam como se fossem uma única pilha de ddp U = 25 V.

Veja um esquema simbólico dessa associação e na sequência das figuras o cálculo da resistência do resistor equivalente Req e da corrente elétrica total i.

O amperímetro indica a corrente que passa por ele que vale i = 2,5 A.

R- D

44-

Relembrando alguns conceitos de plano inclinado:

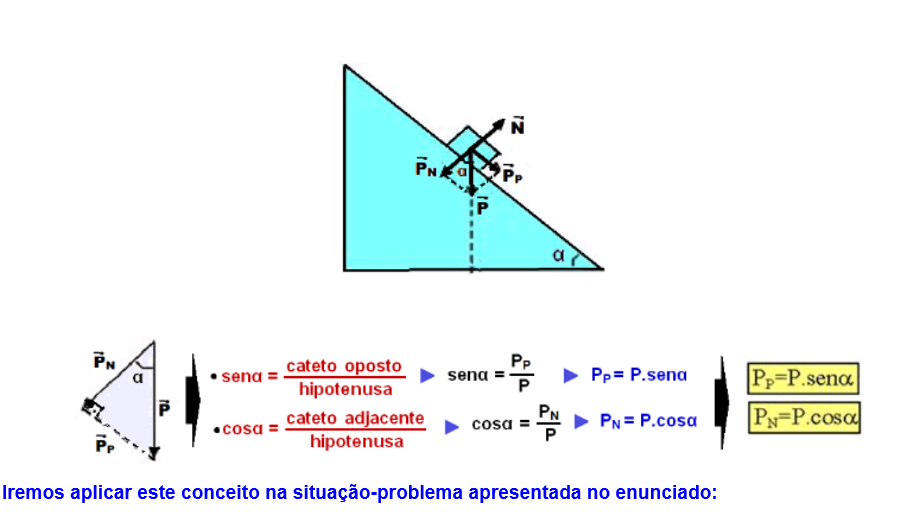
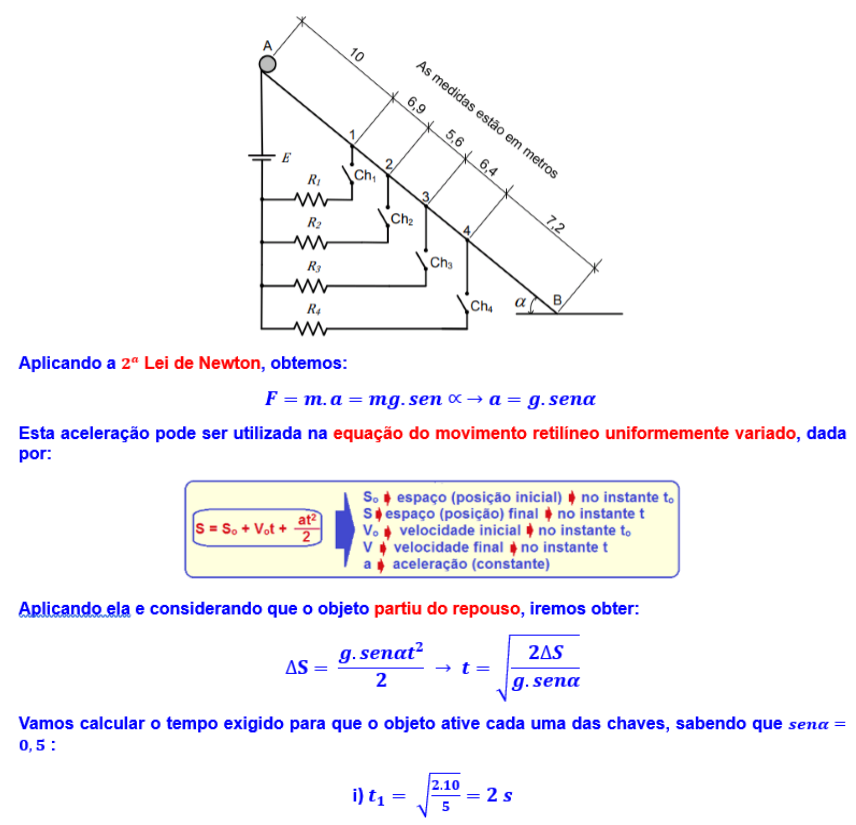
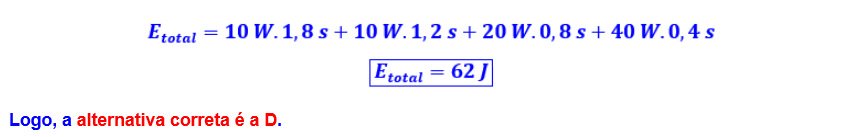
45-

Se as lâmpadas são idênticas cada uma possui a mesma resistência elétrica RL e são percorridas pela mesma corrente iL.

Observe no esquema do circuito que, se o resistor R está sob ddp de U = 3V, cada uma das três lâmpadas terão a mesma ddp (paralelo a ddp é a mesma) de U’ = (12 – 3) = 9 V.

Essa corrente itotal = 0,3 A é a corrente que passa pelo resistor R que está sob ddp de U = 3V.

R- A

46-

1 mA = 10-3 A assim, 10 000 mA = 10 000×10-3 A = 10 A.

R- C

47-

Uma situação prática bastante comum nas residências e nos hotéis é o chamado

“interruptor paralelo”, onde, na realidade a ligação é em série, na qual é possível ligar ou desligar uma determinada lâmpada, de forma independente, estando no ponto mais alto ou mais baixo de uma escada, da maneira indicada nas sequências abaixo.

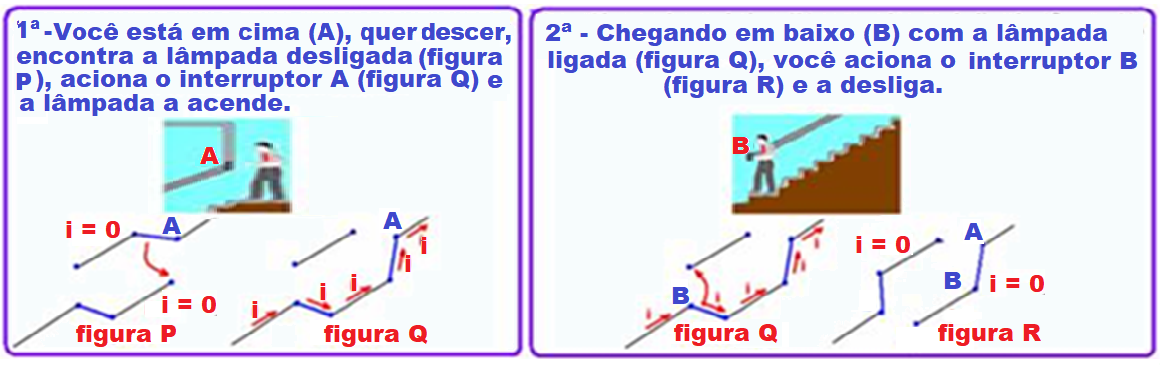
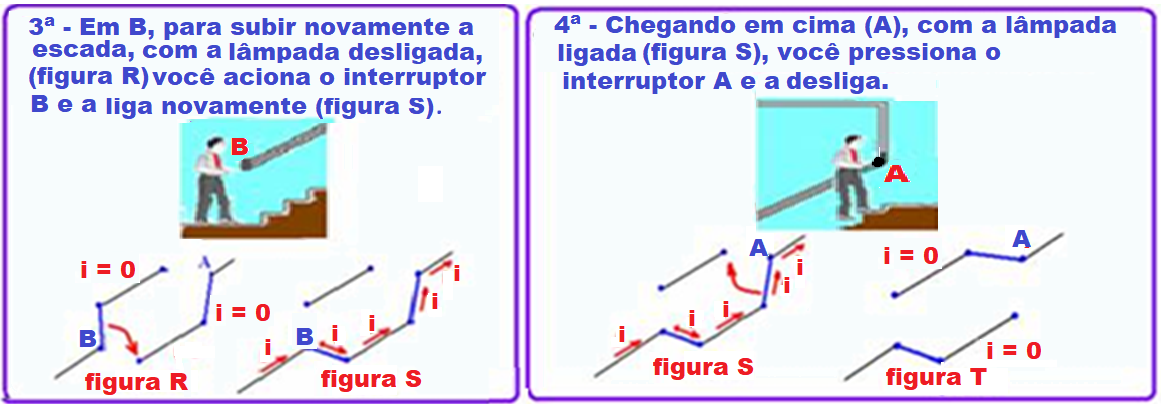
R- E

48-

Se você aumenta a resistência variável R mantendo U constante você estará diminuindo i, pois na expressão R =U/i, com U constante R e i são inversamente proporcionais.

P = E/t, com t constante P e E são diretamente proporcionais.

R- A

49-

Na associação paralelo a resistência do resistor equivalente pode ser calculada por Req = produto/soma = (40 x 10)/(40 + 10) = 400/50 Req = 8 Ω.

Na associação paralelo a tensão U = 12 V é a mesma para os dois resistores P40Ω = U2/R = 122/40 =

144/40 P40Ω = 3,6 W Req = U/i 8 = 12/i i = 1,5 A

R- C

50-

Veja na sequência das figuras abaixo o cálculo da resistência do resistor equivalente:

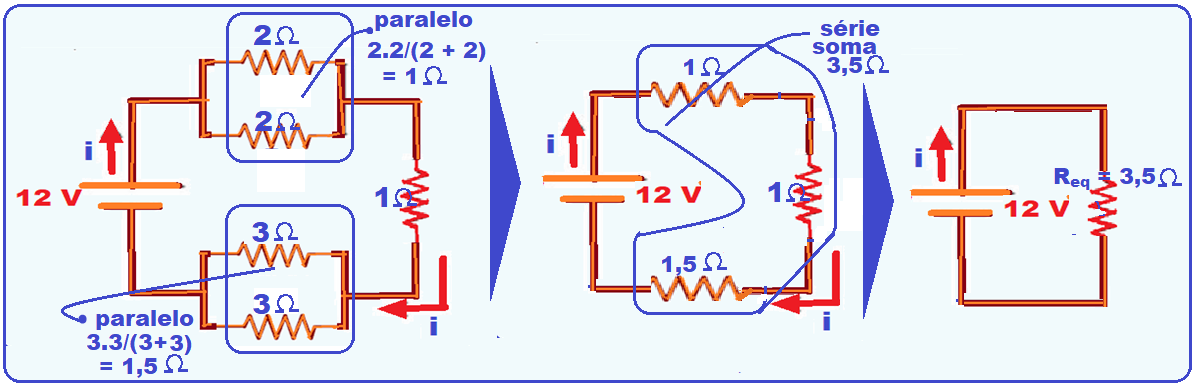
Req = U/i ⇒ 3,5 = 12/i ⇒ i = 3,2 A.

R- B

51-

B. Falsa veja (A).

C. Falsa nas instalações residenciais a associação utilizada é a paralelo (mesma tensão, ddp ou voltagem U).

D. Falsa uma das características da associação série é de que a corrente i é a mesma.

E. Correta;

R- E

52-

Primeiro circuito

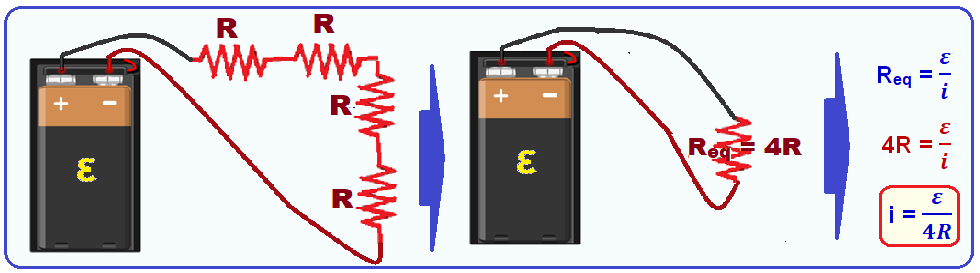
Segundo ciercuito

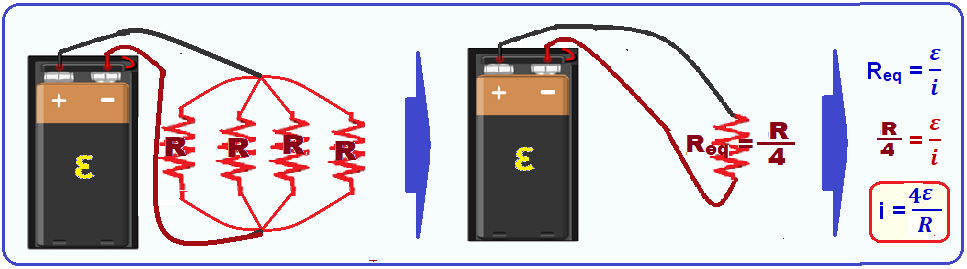
Terceiro circuito

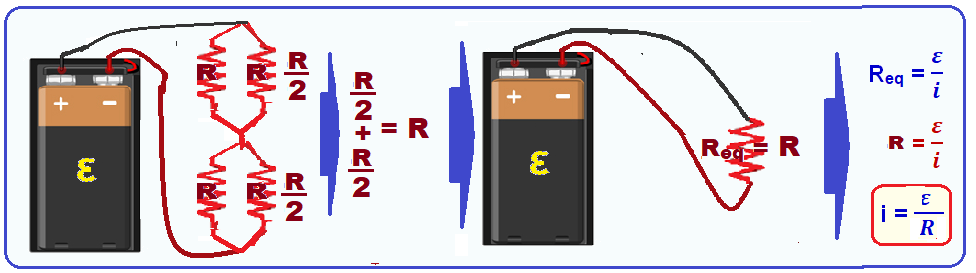
Quarto circuito

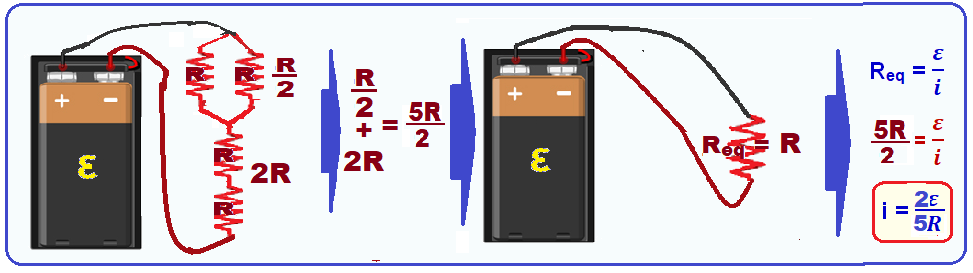
R- C

53-

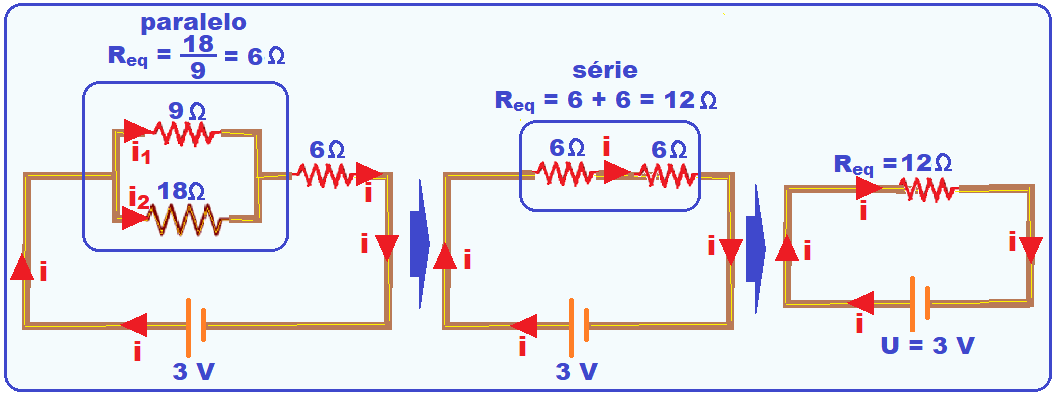
R- B

54-

Observe que a resistência variável Req e o ferro elétrico de resistência RF estão associados em série

R – B

55-

Vamos analisar apenas a parte inferior do circuito onde circulam as correntes i, i1 e i2, já que com

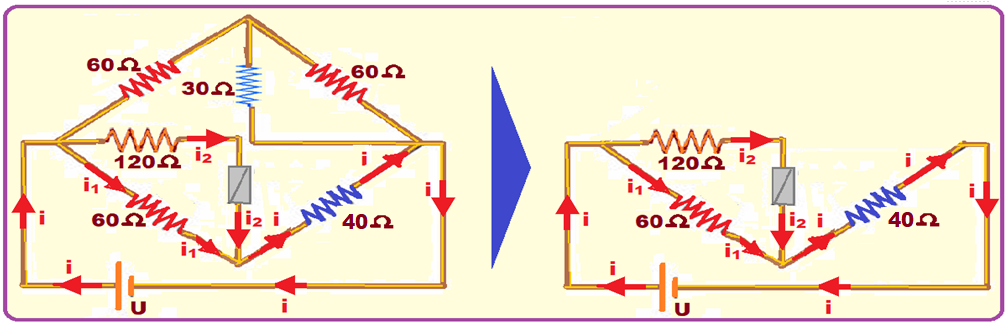
apenas esses dados é possível calcular a tensão U pedida.

Observe que o trecho que possui o resistor de R2 = 120 Ω é percorrido pela corrente i2 = 500 mA = 0,5 A (corrente nominal suportada pelo fusível).

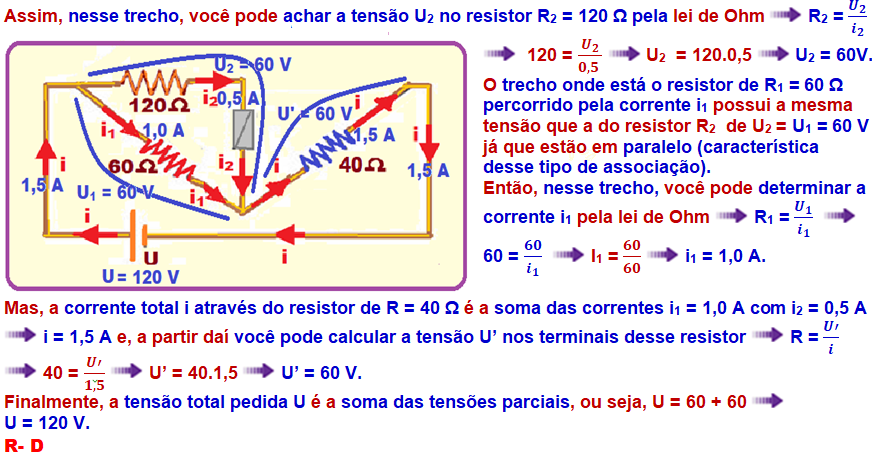
56-

57-

Os valores nominais do LED são P = 8 W e U = 4 V fornecidos pelo enunciado (LED (L) de 8 W, que opera com 4 V).

Pelos valores nominais você pode calcular o valor da resistência do LED através da expressão P =

8 = R = RL = 2 Ω.

Para que o LED opere segundo sua tensão nominal (U = 4 V) ele deverá ser percorrido por uma corrente elétrica de R = 2 = i = 2 A.

Como R e RL estão em série a corrente elétrica neles é a mesma e a resistência do resistor equivalente será Req = R + RL = R + 2.

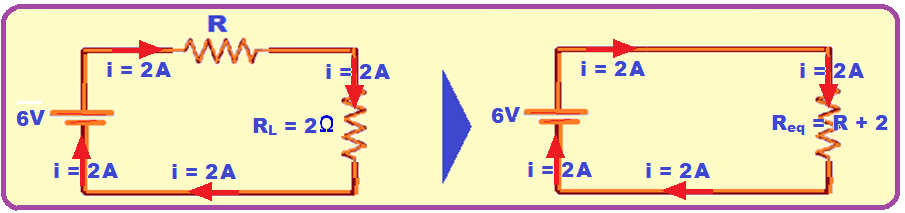Esse Req = R + 2 está ligado na fonte de U = 6 V lei de Ohm Req = R + 2 = R = 3 – 2

R = 1 Ω.

R- A

58-

A figura abaixo mostra um desses isolantes topológicos e, observe que a tensão U é a mesma

para cada resistência (da superfície e do interior) e que elas estão associadas em paralelo.

Características da associação paralelo

Os resistores são associados pelos seus terminais, ou seja, todos saem de um mesmo ponto e todos chegam a um mesmo ponto.

A diferença de potencial (tensão) U de toda a associação (entre A e B) é a mesma para todos os resistores

A corrente total i é a soma das correntes parciais, ou seja, i = i1 + i2 + i3

Fórmulas válidas para a associação paralelo

59-

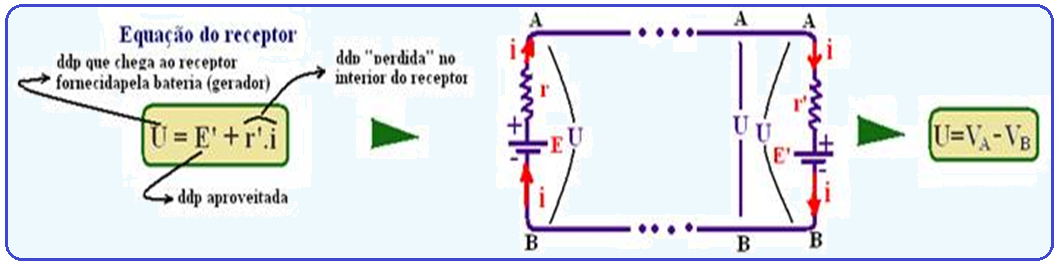
60-

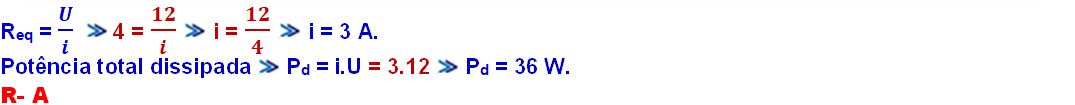
61-

Primeiro, é importante retomar à lei de Ohm:

Pela equação, é possível observar que para manter a tensão U constante, ao diminuir a corrente devemos aumentar a resistência, e ao aumentar a corrente devemos diminuir a resistência. Portanto, como queremos a corrente de menor intensidade, devemos buscar o ramo que oferece a maior resistência. Para isso, vamos calcular a resistência equivalente de cada ramo para podermos comparar. Iremos utilizar as seguintes fórmulas para associações de resistores:

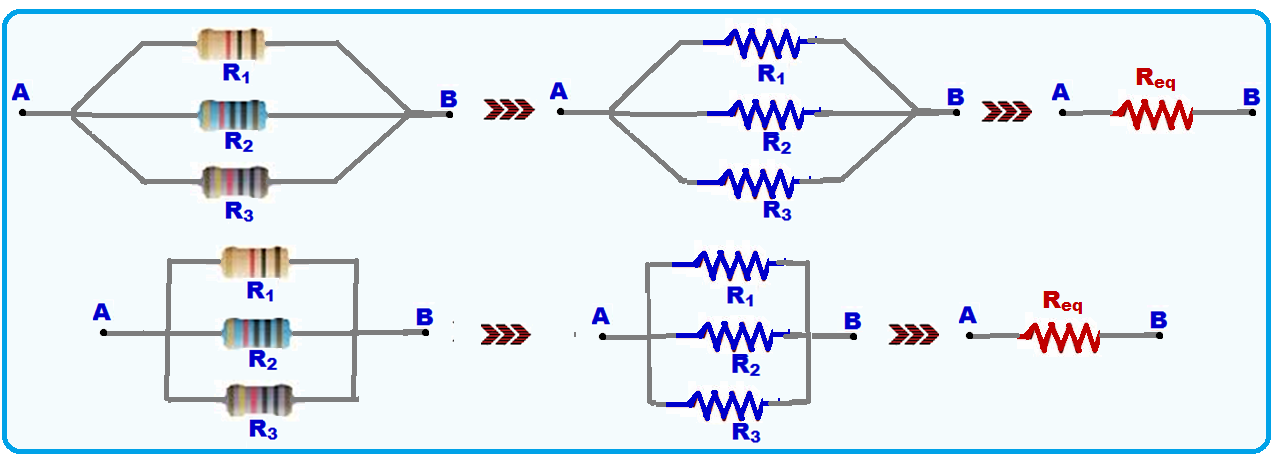
Caso I:

Como podemos ver o caso III tem a maior resistência, então a alternativa correta é então a (C).

62-

63-

A sequência abaixo mostra a representação simbólica do circuito e o cálculo da resistência equivalente Req = 5,8 + r (soma porque (r e 5,8 Ω) estão associados em série).

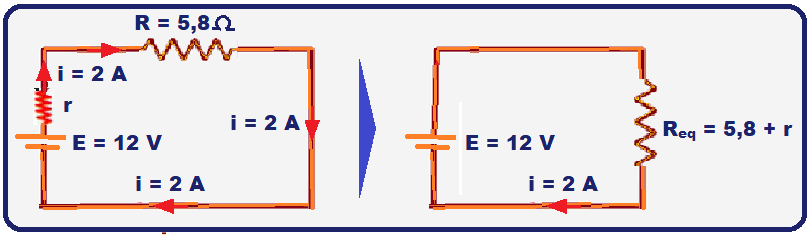
R- B

64-

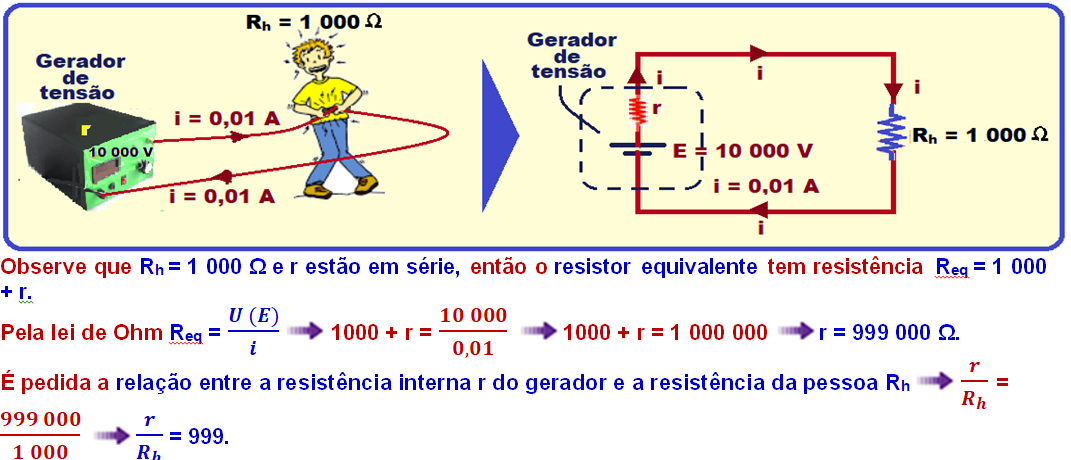
Veja na figura e no esquema abaixo onde E = 10 000 V é a força eletromotriz do gerador, r sua resistência interna, Rh = 1 000 Ω é a resistência corporal da pessoa e i = 0,01 A é a máxima corrente não letal através do corpo da pessoa.

65-

Curva característica de um gerador

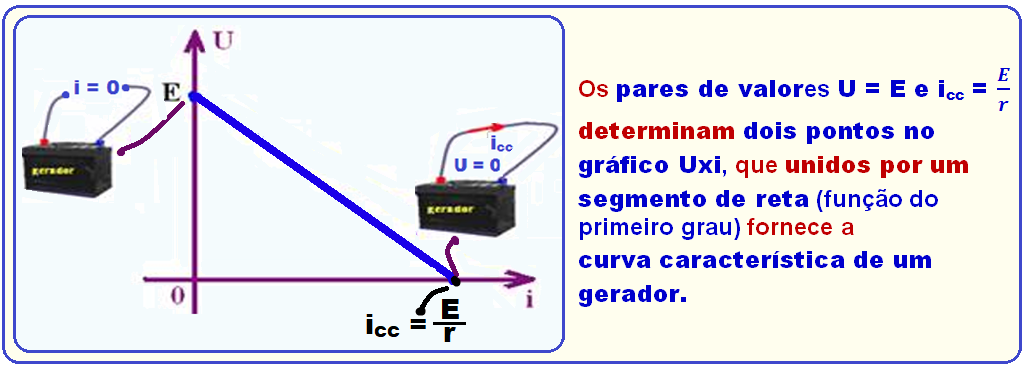
E = força eletromotriz e icc = corrente de curto circuito

R- A

66-

Cálculo da resistência do resistor equivalente onde R = 100 Ω e r = 20 Ω estão em série Req = R + r = 100 + 20 Req = 120 Ω

Cálculo da corrente elétrica i no circuito Req = (U = E)/i 120 = 120/i i 120/120 i = 1 A.

A potência dissipada no gerador é devida a sua resistência interna r = 20 Ω e fornecida por P = r.i2 = 20.12 = 20.1 P = 20 W

R- E

67-

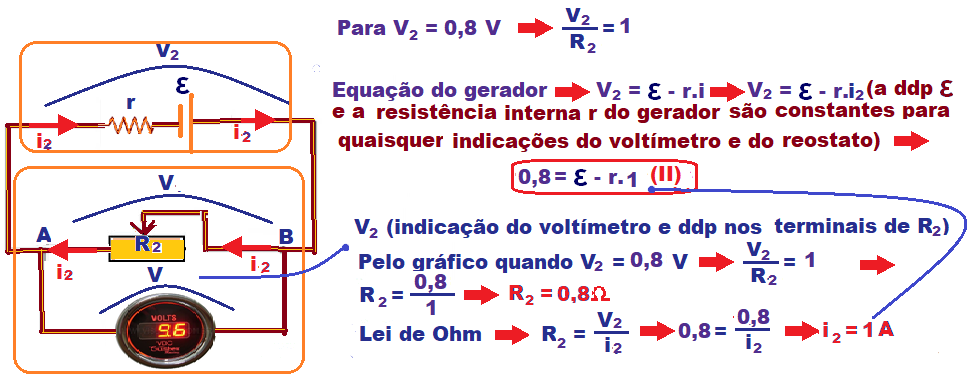
R- B

68-

Representando o circuito por meio dos símbolos convencionais:

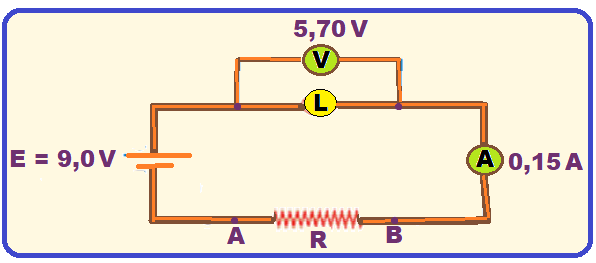
Como os aparelhos de medidas são ideais você pode “curto-circuitar” o amperímetro (resistência interna nula) e retirar o voltímetro (resistência interna infinita).

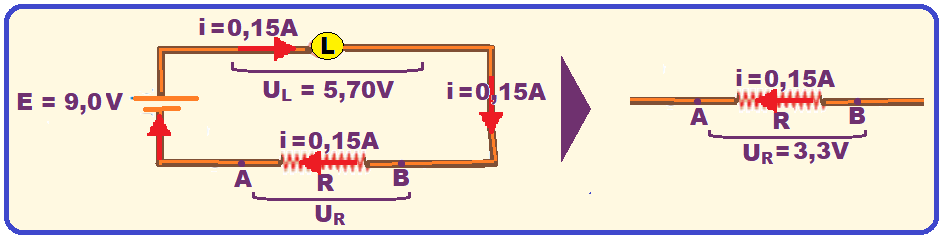
Observe na figura acima que a tensão (ddp ou voltagem) no resistor R vale UR = 9,0 – 5,7 = 3,3 V e que ele é percorrido por uma corrente elétrica de i = 0,15 A (indicação do amperímetro).

R- E

69-

Quando o voltímetro é colocado em contato com os polos da bateria e indicar 12 V ele estará fornecendo o valor da força eletromotriz E da bateria E = 12 V.

A ddp, tensão ou voltagem U nos terminais do resistor de R = 1 kΩ = 1.103 Ω, percorrido por i = 8 mA = 8.10-3 A (indicação do amperímetro) será R = U/i 103 = U/8.10-3 U = 8 V.

Equação do gerador U = E – r.i 8 = 12 – r.8.10-3 r = 4/8.10-3 r = 0,5 .103 = 0,5 kΩ.

R- A

70-

Vamos analisar apenas a parte inferior do circuito onde circulam as correntes i, i1 e i2, já que com

apenas esses dados é possível calcular a tensão U pedida.

Observe que o trecho que possui o resistor de R2 = 120 Ω é percorrido pela corrente i2 = 500 mA = 0,5 A (corrente nominal suportada pelo fusível).

71-

Como as três pilhas estão associadas em paralelo (mesma ddp) elas se comportam como se fossem uma única pilha de ddp U = 25 V.

Veja um esquema simbólico dessa associação e na sequência das figuras o cálculo da resistência do resistor equivalente Req e da corrente elétrica total i.

O amperímetro indica a corrente que passa por ele que vale i = 2,5 A.

R- D

72-

Considerando o galvanômetro ideal, podemos utilizar a fórmula do divisor de corrente para calcular a razão pedida. O divisor de corrente diz que a corrente em um ramo IG será proporcional à corrente de entrada na malha I por um fator de resistência dado por:

73-

Onde U é a tensão imposta no resistor e I é a corrente que passa por ele. Usando essa lei chegamos a:

74-

Primeira lei de Kirchhoff ou lei dos nós: “A soma algébrica das correntes que chegam a um nó é igual à soma algébrica das correntes que saem do mesmo nó”.

Exemplo numérico determine a intensidade da corrente i3 do trecho de circuito abaixo:

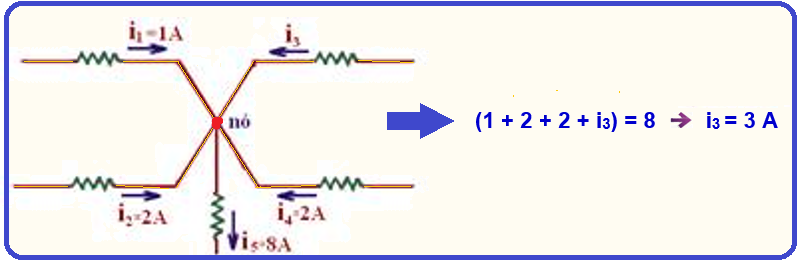
Segunda lei de Kirchhoff ou lei das malhas: “Percorrendo uma malha num mesmo sentido, é nula a soma algébrica das tensões encontradas em cada elemento do circuito”

Baseado na lei acima, escolhendo um sentido de percurso para cada malha, partindo de um ponto, retornando ao mesmo ponto e igualando esta soma algébrica de tensões a zero, você pode estabelecer as seguintes convenções:

Convenção para o sinal de E:

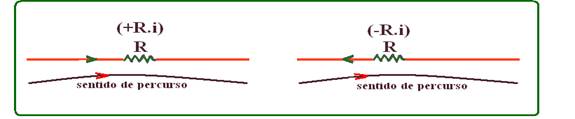
Convenção para o sinal de R.i

Quando o sentido da corrente i coincidir com o sentido do percurso escolhido para a malha, o sinal de R.i será positivo e quando o sentido da corrente i não coincidir com o sentido de percurso escolhido para a malha, o sinal R.i será negativo.

Observe no ponto A que a corrente que chega i é a soma das correntes que saem, ou seja, i = 2 + 6 = 8 A.

Percorrendo a malha I no sentido horário a partir de A, retornando a A e igualando a zero – 8R – 0,5.2 + 5 = 0 8R = 4 R = 0,5 Ω.

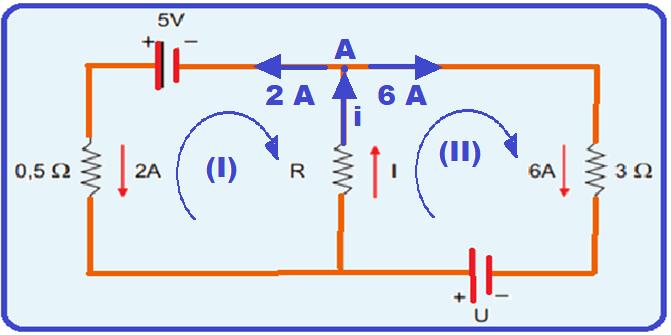
Percorrendo a malha II no sentido horário a partir de A, retornando a A e igualando a zero + 6.3 –U + 0,5.8 = 0 U = 22 V.

R- D

75-

Uma situação prática bastante comum nas residências e nos hotéis é o chamado

R- E

76-