Resolução Comentada Eletrodinâmica – 2017 – 2016 – 2015
Resolução Comentada
Eletrodinâmica – 2017 – 2016 – 2015.
01-
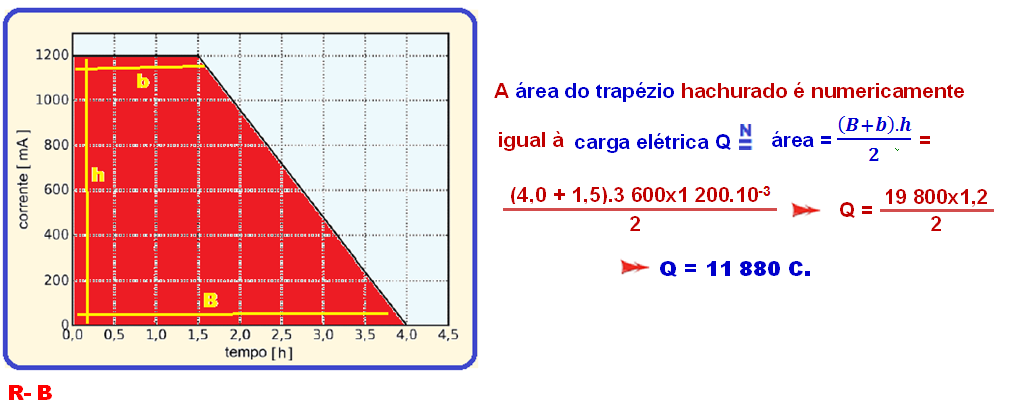
02-
Assim como no cálculo de ΔS em um gráfico V x Δt, nossa carga também pode ser calculada pela área do gráfico, pois como a variação da distância é a multiplicação entre tempo e velocidade, a carga é a multiplicação entre intensidade da corrente e o tempo, logo:
Não podemos esquecer dos coeficientes que multiplicam as unidades, na hora de substituir:
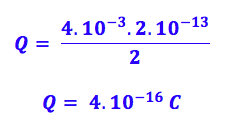
Agora que temos a carga, podemos fazer uma regra de três e achar quantidade de íons:
1 íon -> 1,6.10-19 C
x íons -> 4.10-16 C
Multiplicando em cruz:
Isolando o x:
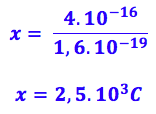
R – A
03-
Como, pelo enunciado, X estava eletrizada com carga de 5,0.10-12 C ela transferiu toda sua carga para Y, ficando X neutra (carga zero).
Acontece que todo corpo ligado à Terra fica totalmente descarregado transferindo integralmente toda sua carga (5,0.10-12 C) para a Terra. Assim Y também ficará neutro com carga zero.
Portanto, no final desse processo, as cargas elétricas totais dos objetos X e Y serão, respectivamente, zero e zero.
R- A
04- Os físicos, Murray Gell-Mann e George Zweig desenvolveram, independentemente, um modelo para classificar as Partículas Elementares. Segundo esse modelo (hoje conhecido como Modelo dosQuarks), os hádrons (bárions, mésons e outras partículas subatômicas)formavam os quarks, que por sua vez eram componentes dos prótons e nêutrons.
R- A
05- Veja a expressão abaixo que relaciona potência elétrica (Po) com energia elétrica (W):
Usa-se também como unidade de medida o kWh onde a potência deve estar em kW = 1000W e o tempo em horas (h).
Lembrando que 
, o ano tem 365 dias e que são 10 painéis que funcionam durante 6 horas por dia, temos:
Por dia e por cada painel, 
Por dia 
(10 painéis)
No ano, com 365 dias, temos, por fim 
Como o exercício pede em kWh 
06-
Diferença diária 
d = (0,21 – 0,0189) 
d = C$ 0,1911 descontando dos C$ 60,00 os 5,00 que ele pagou pela lâmpada incandescente, sobram C$ 55,00, que divididos pela diferença diária de C$0,1011 fornecem 55/0,1911= 287,8 ≈ 288 dias consecutivos.
R- B
07-
R- B
08-
Potência = 
= 
W = Po.∆t = 20x24hx3600s Po = 1 728 000 = 1,728.106 J.
R- B
09-
R- B
10- Para calcular a potência máxima de saída que o carregador pode fornecer você deve utilizar a tensão de saída U = 5 V e a corrente de saída i = 1,3 A, fornecidas nas especificações utilizando a expressão P = i.U = 1,3.5 = 6,5 W.
A carga máxima armazenada na bateria também é fornecida pelasespecificações da bateria Q = 1650 mAh que, transformado em coulomb (C) fornece Q = 1650.10-3.
.3600s 
Q = 5940 C.
R- D
11- Observe na expressão P=U2/R que, sendo a resistência elétrica R constante, a potência é diretamente proporcional ao quadrado da voltagem U. Assim, se ele for ligado a uma voltagem duas vezes menor (220 V para 110 V), a potência ficará 22 = 4 vezes menor.
R- D
12- P = W/∆t— lâmpada — 60 = Wl/3600 — Wl = 216 000 J
P = W/∆t— televisão — 90 = Wt/3600 — Wt = 324 000 J
A televisão consome mais energia elétrica, mas a tensão em cada aparelho é a mesma, pois estão associados em paralelo.
R- D
13- Veja abaixo a expressão matemática da segunda lei de Ohm:
A resistência elétrica R é diretamente proporcional ao comprimento l do fio e à resistividade ρ (característica do material que constitui o fio) e inversamente proporcional à área se seção reta transversal (S) “grossura do fio”.
Assim, se você dobrar o comprimento do fio estará dobrando o valor da resistência elétrica R do mesmo.
R1 = R e R2 = 2R
Corrente i1 no fio de comprimento L submetido à voltagem U — R1 = U/i1 — i1 = U/R. (I)
Corrente i2 no fio de comprimento 2L submetido à voltagem U — R2 = U/i2 — i2 = U/2R. (II)
Comparando (I) com (II) — i1 =2i2.
R- A
14- Segunda lei de Ohm 
R = ρL/A.
Resistor 1 R1 = ρ2L/A resistor 2 R2 = ρL/2A.
Resistor equivalente Req = R1 + R2 = ρ2L/A + ρL/2A = 5ρL/2A.
Req = V/i 
i = V/Req = V/5ρL/2A i = 2AV/5ρL.
R- A
15-
a) a resistência equivalente, em Ω.
Observe a sequência abaixo para o cálculo da resistência equivalente Req no circuito da figura 2, onde os três resistores estão em paralelo:
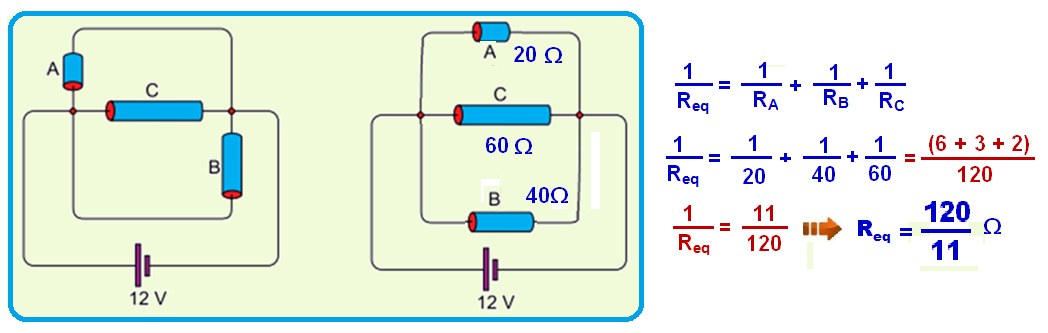
b) a potência total dissipada, em W.
Você pode calcular a potência total dissipada utilizando a resistência equivalente que está submetida à uma tensão de U = 12 V.
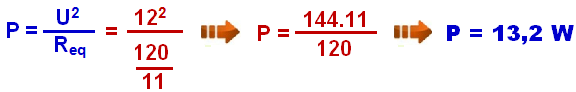
16-
Com o ohmímetro conectado entre A e B você deve calcular a resistência do resistor equivalente RAB entre esses dois pontos.
Assim, o circuito ficará conforme a figura (1), onde os dois resistores de 10 kΩ estão em série podendo ser substituidos por um único resistor de(10 kΩ + 10 kΩ) = 20 kΩ.
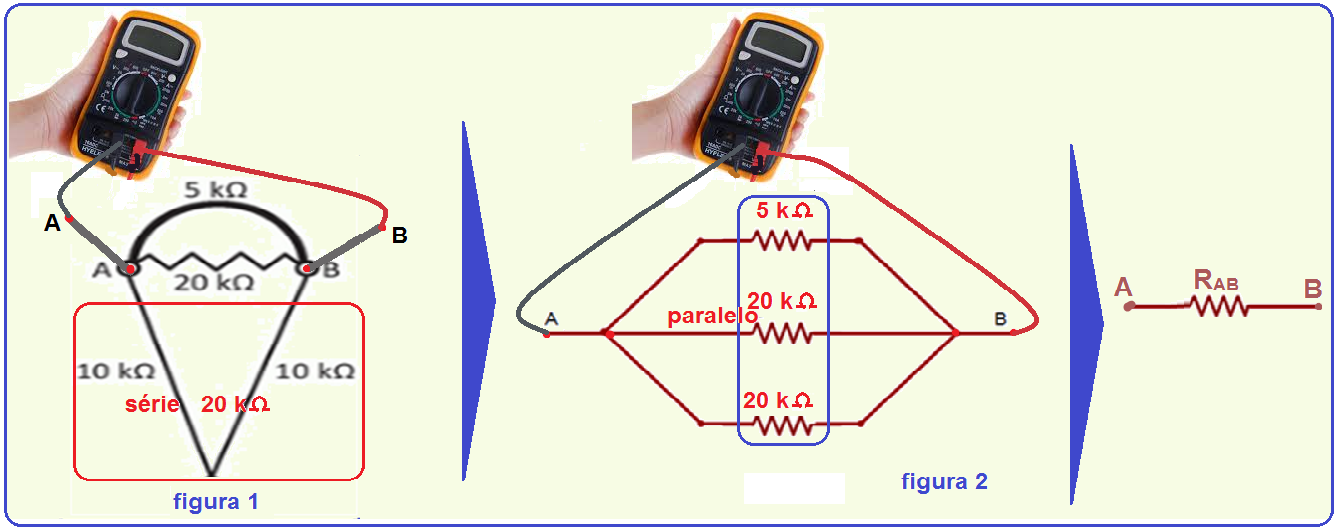
Com o ohmímetro conectado entre B e C você deve calcular a resistência do resistor equivalente RBC entre esses dois pontos.
Observe na sequência abaixo o cálculo da resistência entre B e C, RBC .
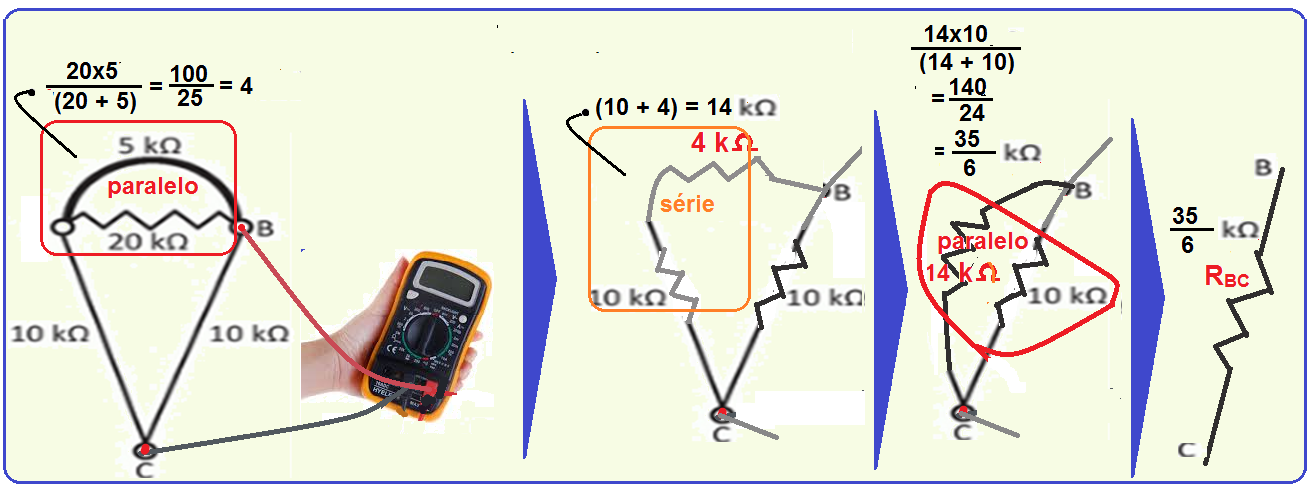
17- Calculando a resistência do resistor equivalente entre os pontos A e B da figura que mostra os trechos pelos quais não circula corrente elétrica (circuito em aberto):
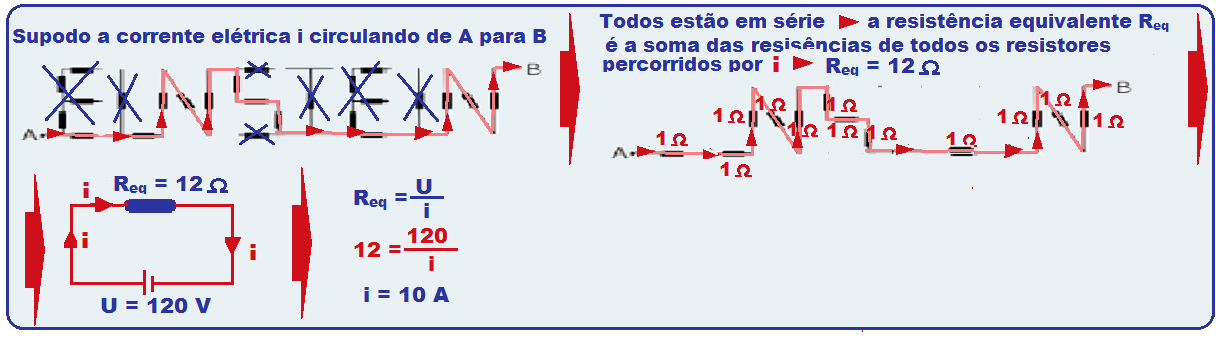
Então, a intensidade de corrente elétrica que irá aquecer a água do aquário é de i = 10 A.
Agora vamos calcular a quantidade de energia térmica (calor)W que irá aquecer a massa de água do aquáriom = 120000 g, de calor específico c= 1g.cm-3.oC-1 de modo que sofra uma variação de temperatura ∆Ɵ = 36oF = 20oC.
18- Cálculo da resistência equivalente e da fem do gerador com a chave C aberta:
Essa fem ε = 15R é constante, pois o gerador é o mesmo:
A sequência de figuras abaixo mostra o cálculo da resistência do resistor equivalente com a chave C fechada e retirando o amperímetro ideal (resistência interna nula):
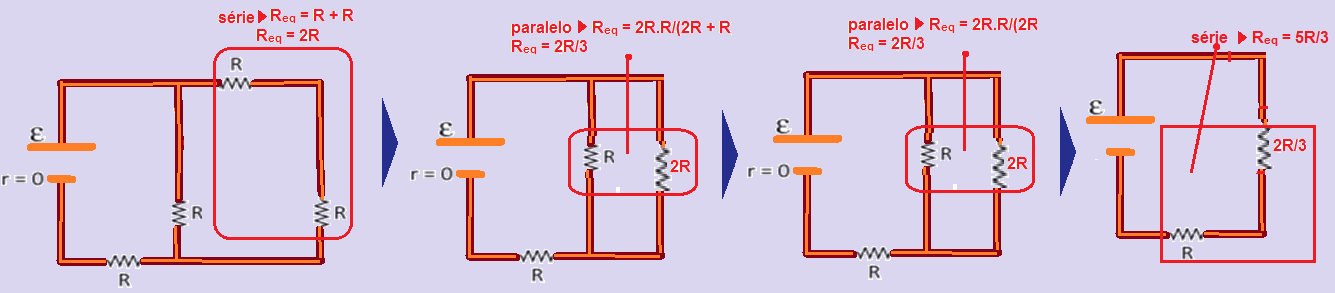
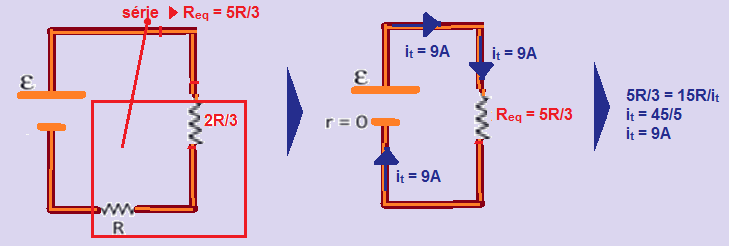
Observe atentamente na figura abaixo que a corrente elétrica indicada pelo amperímetro é iA = 3 A.
R- E
19- Para que as tomadas, como pede o enunciado estejam submetidas à mesma diferença de potencial (ddp), tensão ou voltagem U, essas duas tomadas devem estar ligadas em paralelo já que nesse tipo de associação a tensão é a mesma que a tensão nominal da rede elétrica (U).
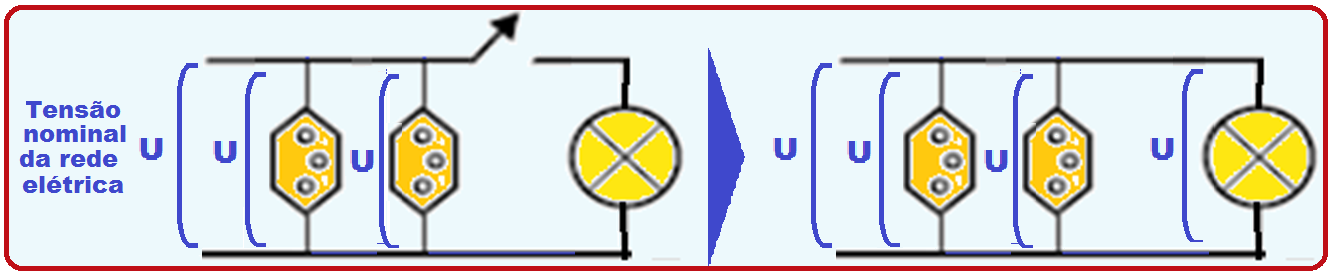
Mas, o interruptor deve estar ligado em série com a lâmpada e, quandofechado ele acende a lâmpada que fica em paralelo com as tomadas e, portanto, submetida à tensão nominal (U) da rede que as tomadas.
Desligando o interruptor, desliga-se a lâmpada, sem alterar a ligação paralelo das tomadas com a rede, que continuam sujeitas à mesma ddp nominal U, da rede.
R- E
20- No chuveiro elétrico, podemos alterar a resistência elétrica equivalente através da variação do comprimento do resistor.
R- A
21- a) Cálculo da intensidade de corrente elétrica i utilizando os valores nominais fornecidos: P = 25 W e U = 40 V 
P = i.U 25 = i.40 i = 
= 0,625 A.
A carga elétrica ∆Q no intervalo de tempo ∆t = 20 minx60 = 1200 s pode ser determinada por i = 
0,625 = 
.
b)
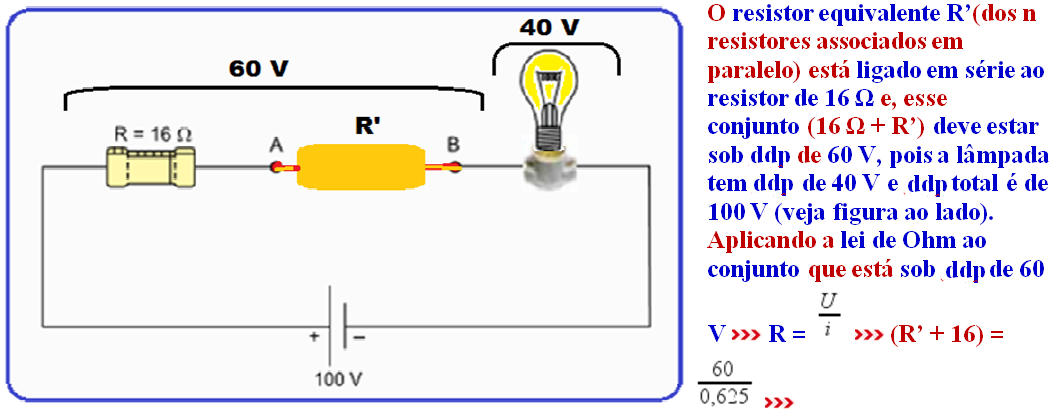R’ + 16 = 96 R’ = 80 Ω.
Então, você deve associar em paralelo n resistores de 320Ω de maneira a obter um único resistor de 80 Ω n = 
n = 4.
22- Trata-se de uma associação de resistores (lâmpadas) associados em paralelo e, cujas características são fornecidas a seguir:
Características da associação paralelo
Os resistores são associados pelos seus terminais, ou seja, todos saem de um mesmo ponto e todos chegam a um mesmo ponto.
A diferença de potencial (tensão) U de toda a associação (entre A e B) é a mesma para todos os resistores
A corrente total i é a soma das correntes parciais,ou seja, i = i1 + i2 + i3.
No caso do exercício:
Observe que a intensidade de corrente iA (corrente total) que sai do polo positivo da bateria deve ser a mesma que iE que chega ao polo negativo da mesma bateria.
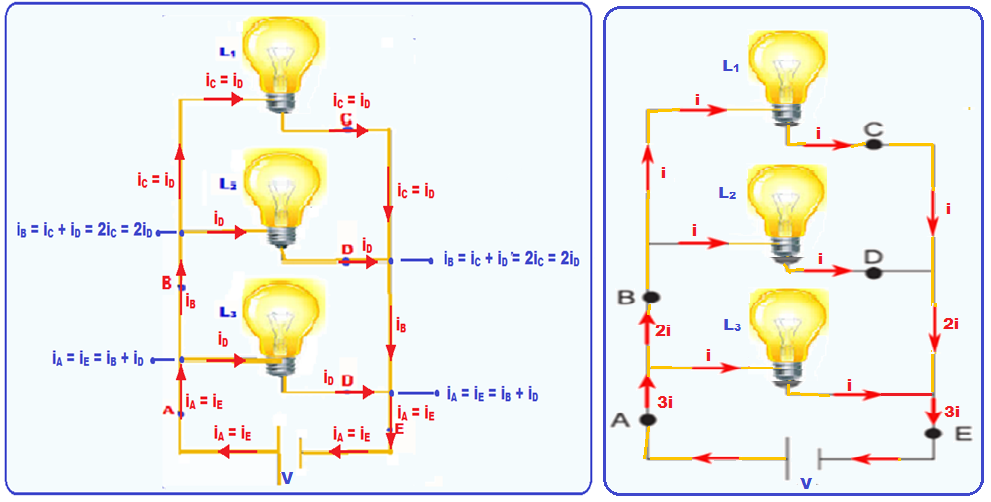
Como, pelo enunciado, as lâmpadas são idênticas elas possuem a mesma resistência e, consequentemente são percorridas pela mesma corrente elétrica, ou seja, iC = iD.
R- A
23-
24-
Observe que a alternativa correta é a C, cuja análise é feita a seguir:
Na sequência abaixo é fornecido o cálculo da corrente elétrica total i.
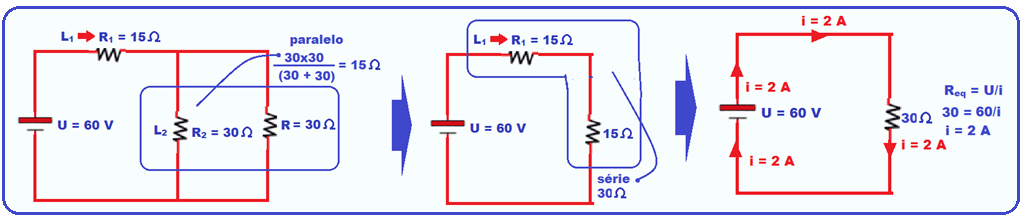
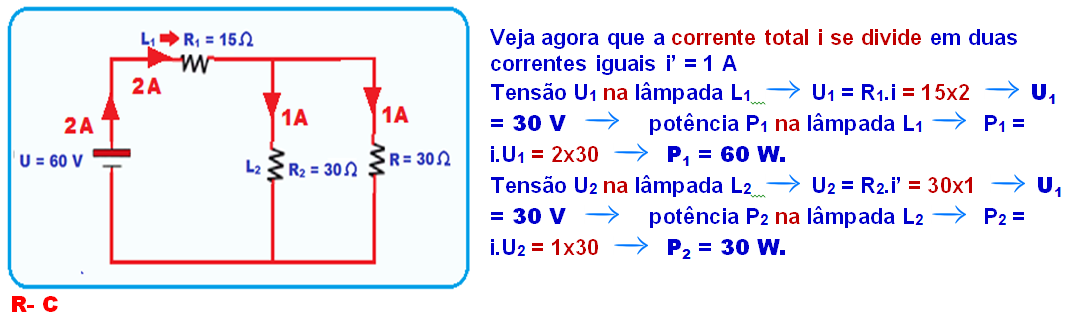
25- 
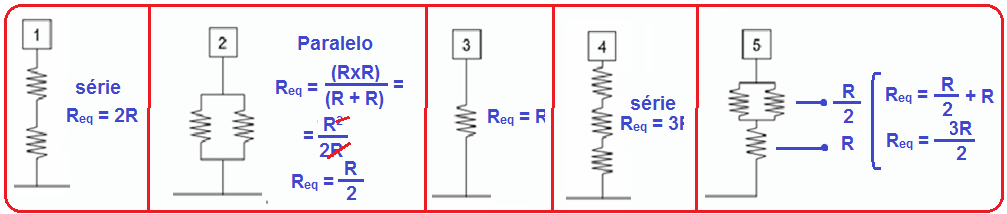
Observe que o circuito de número 2 possui menor resistência elétrica equivalente, portanto será percorrido por maior corrente elétrica.
R – A
26- a) Cálculo da resistência equivalente ReqA quando a chave está ligada no ponto A e a corrente
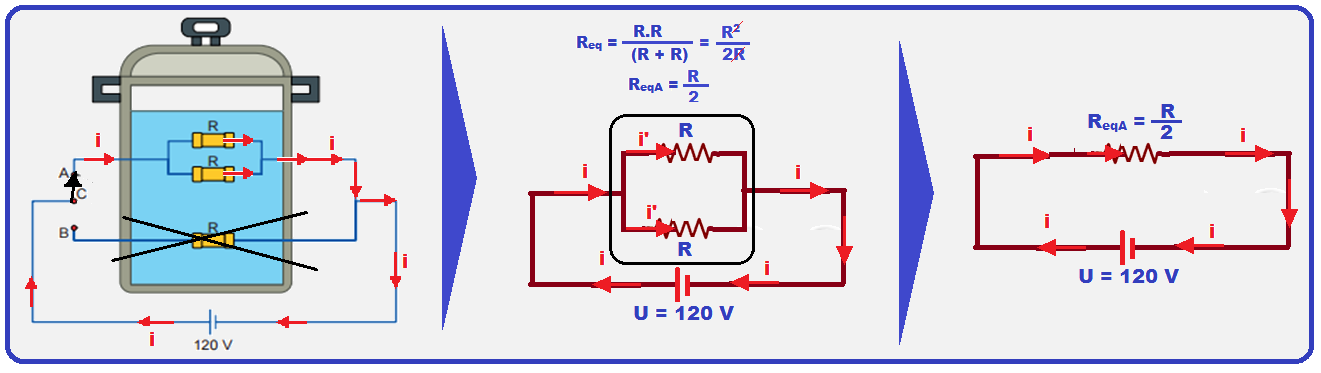elétrica passando apenas pelos dois resistores que estão em paralelo.
b) Se a densidade da água é d = 1 kg/L, isso significa que o volume de 1 L de água possui massa de m = 1 kg.
Assim, o volume de 4L de água equivale à massa de m = 4 kg.
Da equação fundamental da calorimetria 
Q = m.c.∆θ = 4.1.(80 – 20) = 4.60 Q = W = 240 kcal.
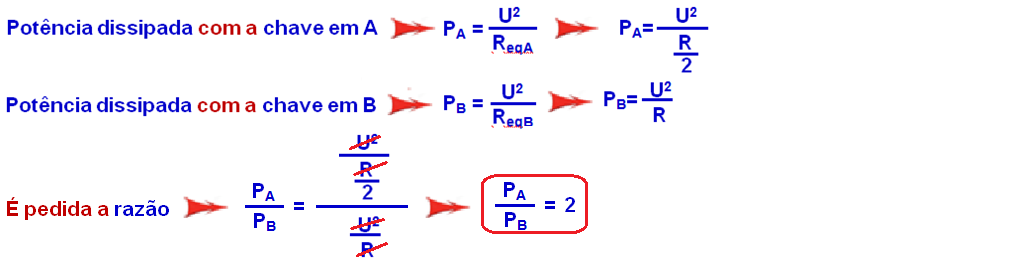
Com a chave em A PA = 
= 
= 
PA = 400 W.
PA = 
2.40 = 
R = 
R = 18 Ω
27- Sendo o voltímetro ideal ele possui resistência interna infinita (isolante), por ele não circula corrente elétrica, então você pode retirá-lo do circuito, que fica conforme a figura abaixo:
Na sequência a seguir está sendo calculada a resistência elétrica do resistor equivalente:
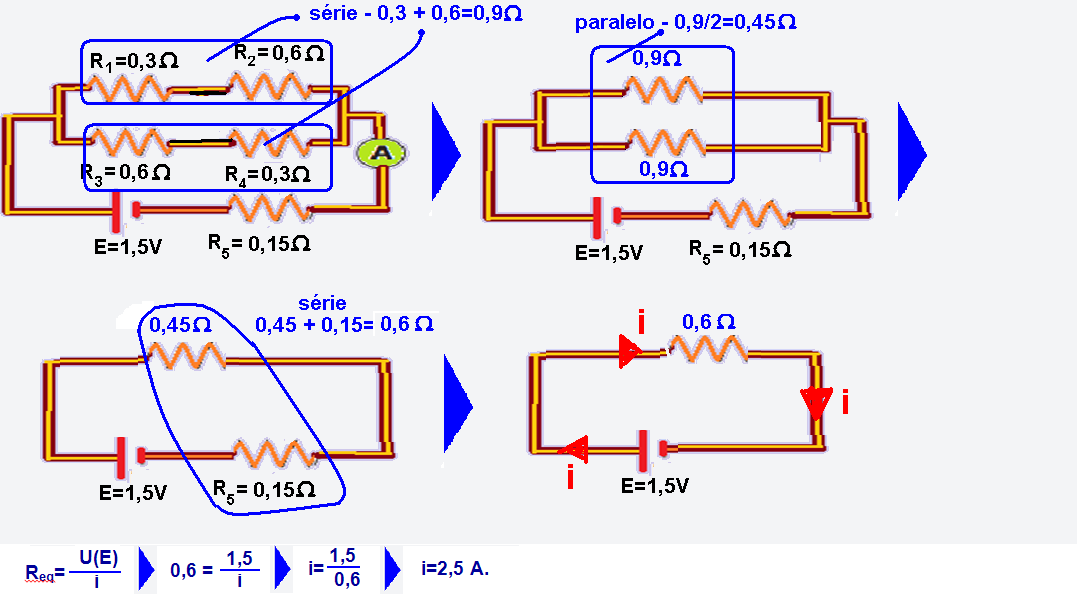
Veja na figura abaixo que a corrente elétrica que circula peloamperímetro (indicação do mesmo) é de 2,5A e veja também as correntes que circulam por cada resistor:
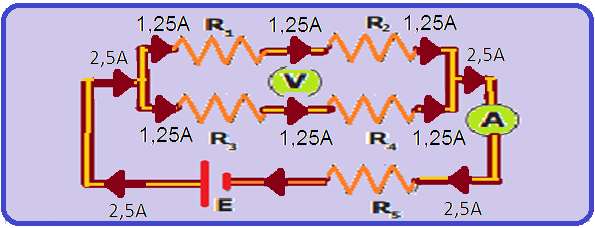
A diferença de potencial (tensão, voltagem) entre A e B é fornecida porUAB=R.i=0,3.1,25=0,375V.
A diferença de potencial (tensão, voltagem) entre A e C é fornecida por UAC = R.i = 0,6.1,25 = 0,75V.
UAB = VA – VB — VA – VB = 0,375V — UAC = VA –VC — VA – VC = 0,75V.
UAC – UAB = 0,75 – 0,375 = 0,375V — (VA – VC) – (VA – VB) = 0,375 = VA – VC– VA + VB — VB – VC = 0,375V.
Observe na figura que o voltímetro está inserido entre os pontos B e C então ele indicará a ddp entre esses dois pontos, ou seja, indicará UBC = 0,375V.
R- A
28- Observe que o dispositivo de 8V (maior valor) é o gerador (a corrente sai de seu polo positivo) e o de 6 V é o receptor (a corrente sai de seu polo negativo) 
U = 8 – 6 = 2V.
Os resistores estão associados em série Req = 3 + 3 + 4 = 10 Ω.
Req = 
10 = 
i = 0,2 A (corrente em cada resistor) P4Ω = R.i2 = 4.(0,2)2 = 4.0,04
P4Ω = 0,16 W.
R- A
29- Vamos começar o exercício analisando o valor de corrente dado no enunciado, através da fórmula da resistência:
Aonde: R é a resistência elétrica = 10kΩ.
U é a tensão da corrente (ddp).
i é a corrente elétrica = 1 mA.
Isolando o U:
Substituindo:
Resolvendo:
U = 10 V
Esse resultado é importante para nos mostrar que os outros dois resistores não podem estar em série, visto que se estivessem cada um teria uma tensão de 10 V, somados teriam uma tensão geral de 30 V, maior que a do enunciado. Como os resistores não podem estar em sérieeles só podem estar em paralelo. Formando um circuito exemplificado na imagem abaixo:
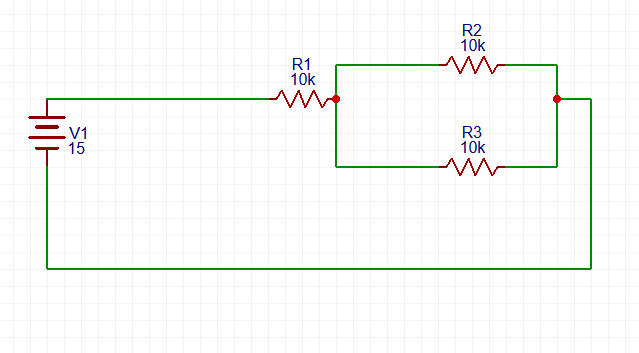
A resistência total vai ser a soma do resistor R1 com a soma da resistência em série dos outros dois resistores, vamos calcular essa resistência em série pela fórmula abaixo:
= 
Substituindo os valores:
= 
Calculando:
= 
Simplificando:
= 
Elevando ambos os lados por -1:
R = 
Ω
Somando com o outro resistor para achar a resistência total:
R = + 10.10³
R = 
Ω
R = 
Ω
R- D
30- 01) Os resistores equivalentes nos dois ramos do circuito possuem, respectivamente, resistência elétrica de 30 Ω e de 5 Ω.
01. Correta 
ramo A série Req = 10 + 10 + 10 = 30 Ω ramo B paralelo Req = 10.10/(10 + 10) = 100/20 Req = 5 Ω.
02) A corrente elétrica que flui no ramo A é de 2 A.
02. Falsa Req = U/i 30/7 = 10/i i = 2,33 A iA = 10/30 = 0,33 A iB = 10/5 = 2 A.
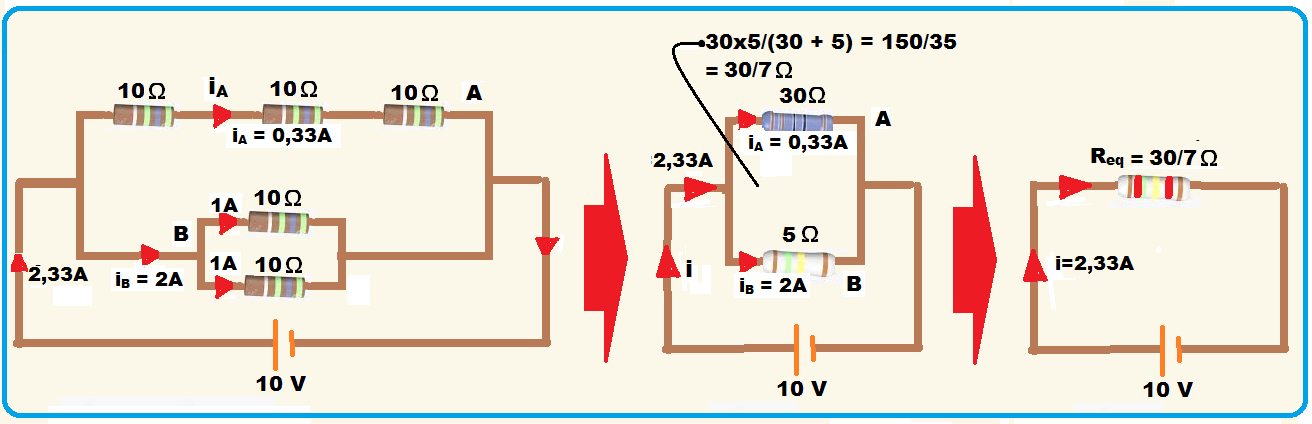
Veja acima que iA = 0,33 A.
04) A potência dissipada no ramo B é de 20 W.
04. Correta P = R.iB2 = 5.22 = 20 W.
08) A potência dissipada e a corrente elétrica no ramo B são maiores que as observadas no ramo A.
08. Correta de 04, PB = 20W PA = R.iA2 = 30.0,33 = 9,9 W.
16) A diferença de potencial entre os terminais do segundo resistor do ramo A é de aproximadamente 3,3 V
16. Correta R = U/iA 10 = U/0,33 U = 3,3 V.
R- (01 + 04 + 08 + 16) = 29
31-
Veja um resumo da teoria a seguir:
Curva característica do gerador – é representada por um gráfico que relaciona a intensidade de corrente elétrica i no gerador com a diferença de potencial (tensão) U em seus terminais.
Se i=0, ou seja, se o gerador estiver em circuito aberto, tem-se:
Se U=0, ou seja, se o gerador estiver em curto circuito, tem-se:
Os pares de valores U=E e icc=E/r determinam dois pontos no gráfico Uxi, que unidos
por um segmento de reta (função do primeiro grau) fornece acurva característica de um gerador.
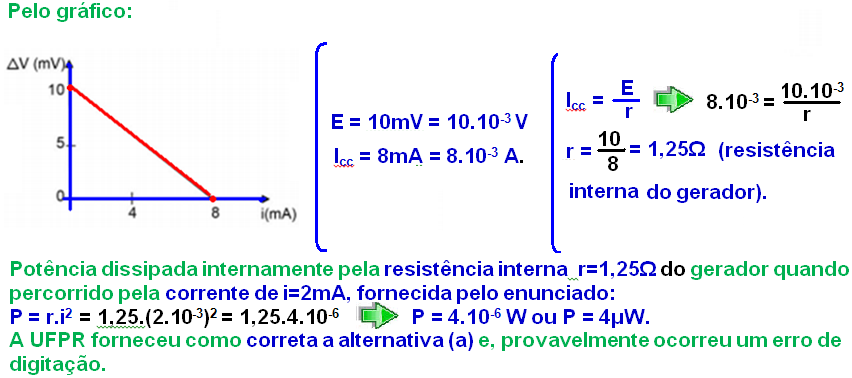
32- Na situação 1, como o voltímetro é ideal, possui resistência interna infinita, isolante), você pode retirá-lo e calcular a resistência equivalente conforme a sequência abaixo:
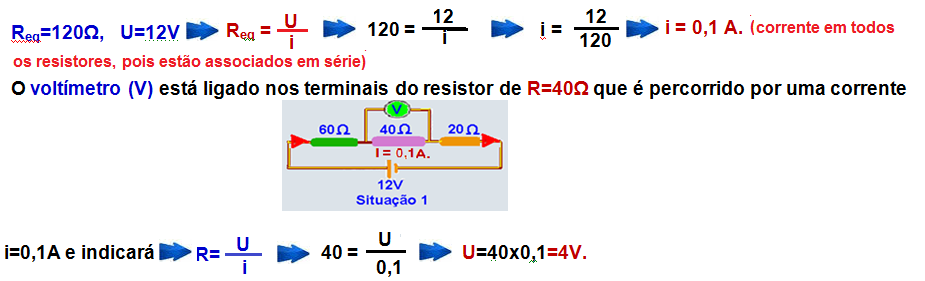
Na situação 2 o amperímetro está ligado em série e, como ele é ideal(resistência interna nula) você pode curto-circuitá-lo e calcular a resistência equivalente conforme a sequência abaixo:
Req=U / i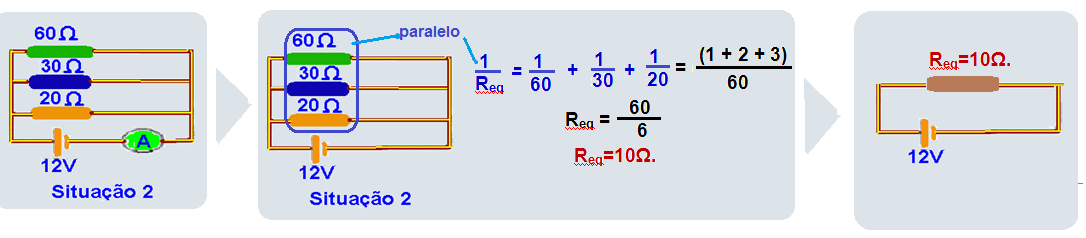
R- B
33- Refazendo simbolicamente o circuito:
Sendo os aparelhos de medida ideais você pode “curto-circuitar” o amperímetro,retirar o voltímetro e calcular a resistência equivalente na seqüência abaixo:
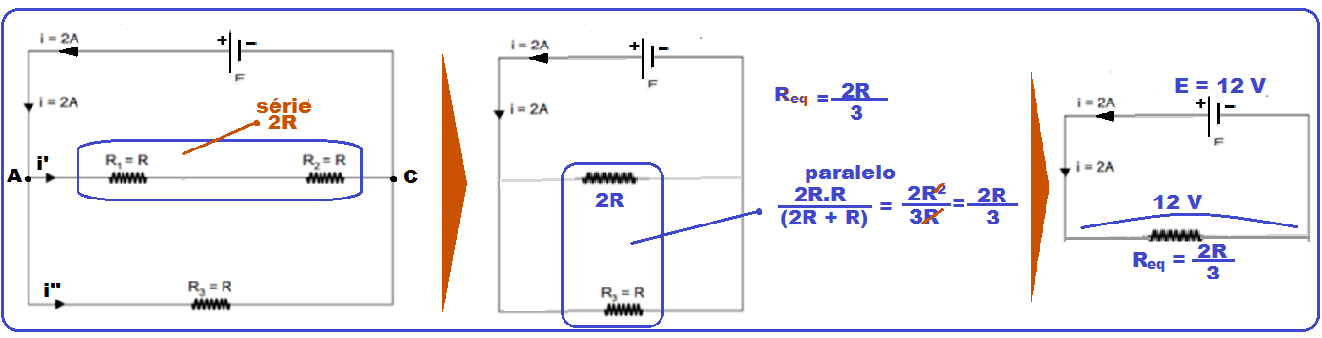
34- Observe que as duas lâmpadas acesas de mesma potência P = 60 W e sob tensão de U = 12 V estão associadas em paralelo e, ambas também em paralelo com a bateria de U = 12 V o que é óbvio, pois a tensão U é a mesma.
Assim, usando os valores nominais fornecidos a corrente elétrica i em cada lâmpada será a mesma e fornecida por P = i.U 60 = i.12 i = 5 A.
Veja na figura abaixo que a corrente que passa pelo fusível deve valer if = 2.i = 2.5 if = 10 A.
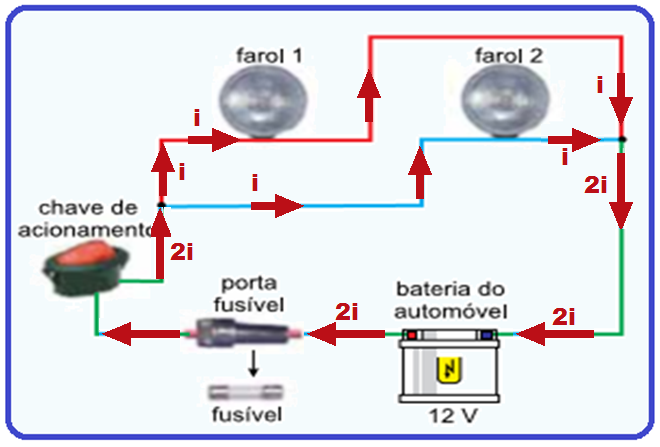
Das alternativas, aquela cujo fusível apresenta menor amperagem(intensidade de corrente elétrica)
capaz de proteger esse circuito é o de 12 A.
R- B
35-
Na situação 1, como o voltímetro é ideal, possui resistência interna infinita, isolante), você pode retirá-lo e calcular a resistência equivalente conforme a sequência abaixo:
Na situação 2 o amperímetro está ligado em série e, como ele é ideal(resistência interna nula) você pode curto-circuitá-lo e calcular aresistência equivalente conforme a sequência abaixo:
Req=U / i
R- B