Resoluções – Eletrodinâmica – 2014 – 2013
Resoluções Vestibulares Recentes
Eletrodinâmica – 2014 – 2013
01- Cálculo da resistência elétrica R da lâmpada pelas especificações — P=U2/R — 24=122/R —
R=144/24 — R=6Ω.
Sendo essa R=6 Ω constante, quando a lâmpada estiver sob ddp (tensão) de 6V a corrente i que circula por ela será — R=U/i — 6=6/i — i=1 A.
Potência elétrica dissipada pela lâmpada quando sob ddp de U=6V — P=R.i2 = 6.12 — P=6W.
R- A
02- a) Observe na figura fornecida que a resistência equivalente Req está entre os pontos A e B:
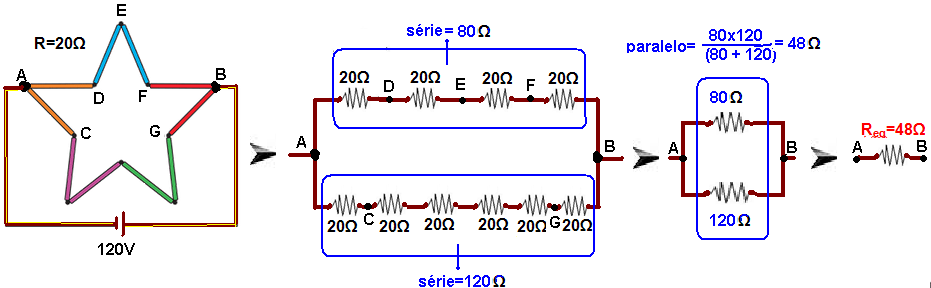
Req=48Ω
b) Como os ramos superior e inferior estão associados em paralelo a tensão U=120V é a mesma em cada um — sendo a resistência R=20Ω de cada barra (resistor) a mesma, a tensão em cada resistor do ramo superior vale Us=120/4=30V e em cada resistor do ramo inferior vale Ui=120/6=20V
A potência elétrica dissipada em cada resistor (barra) do ramo superior vale Ps=Us2/R=302/20=45W e em cada resistor do ramo inferior vale Pi=Ui2/R=202/20=20W
Cores laranja; uma no ramo superior (45W) e outra no inferior (20W) — Pl=45 + 20 — Pl=65W
Cores azul; duas no ramo superior (2x45W=90W) — Pa=90W
Cores vermelha; uma no ramo superior (45W) e outra no inferior (20W) — Pv=45 + 20 — Pv=65W
03- Colocando a chave na posição B você terá o circuito da figura abaixo cuja sequência nos
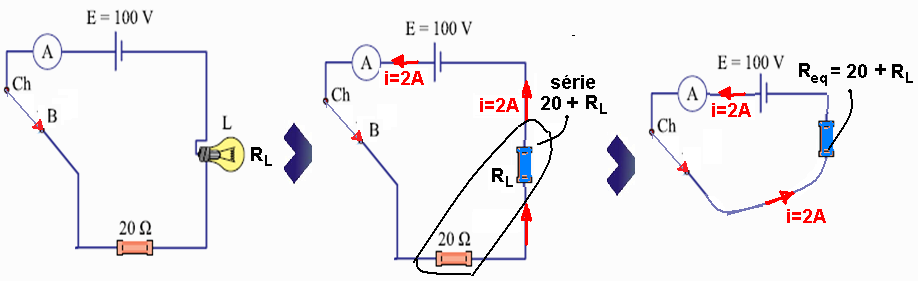
fornece o resistor equivalente Req=20 + RL — Req=U(E)/i — 20 + RL=100/2 — 20 + RL=50 — RL=30Ω.
Veja que o enunciado afirma que, com a chave em B onde i=2A, a potência elétrica dissipada pela lâmpada é de Pd=60W, o que nos forneceria uma resistência de — P=RL.i2 — 60=RL.22 — RL=15Ω.
Como o exercício afirma que a resistência da lâmpada é constante, essa potência fornecida de 60W é incompatível e vamos ignorá-la na continuação do exercício e considerar a resistência da lâmpada como seno RL=30Ω.
Colocando agora a chave em A, a nova resistência equivalente será Req=45 + 20 + 30=95Ω (figura).
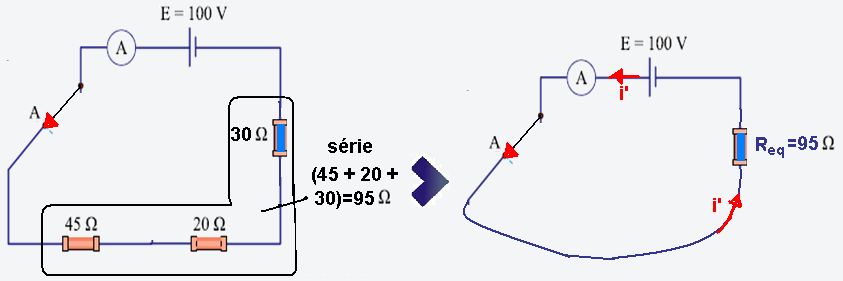
Req=E/i’ — 95=100/i’ — i’=100/95≈1A — potência dissipada pelo circuito — P=Req.i2=95.12=95W.
Energia elétrica dissipada pelo circuito durante Δt=2min=2.60=120s — W=P.Δt=95.120 —
W=11400J=1,1.104J.
04- A) Falsa — desligando-se L1, L2 manterá seu brilho já que será percorrida pela mesma corrente que antes pois, como estão em paralelo a tensão U é a mesma antes e depois de desligar L1 e a potencia de L2 também será a mesma já que P2=U2/R e R também é a mesma.
B) Falsa — pela segunda lei de Ohm R=ρℓ/S e, sendo o material (ρ) o mesmo e o comprimento (ℓ) do filamento o mesmo, a lâmpada 2 que é mais grossa (maior S), possuirá menor resistência elétrica R e, consequentemente será pecorrida por maior corrente elétrica brilhando mais
C) Falsa — os filamentos possuem resistências elétricas diferentes possuindo diferentes brilhos.
D- Correta — veja (B)
R- D
05- Usando os valores nominais de cada lâmpada idênticas você pode calcular o valor da resistência elétrica de cada uma pela expressão P=U2/R — 100=1002/R — R=100Ω.
Observe na figura abaixo que a lâmpada L1 de resistência R=100 Ω, é percorrida por i1, e pelo enunciado sob potência de 100W, tal que — P1=R.i12 — 100=100. i12 — i1=1 A (corrente por L1 quando sob potência de 100W).
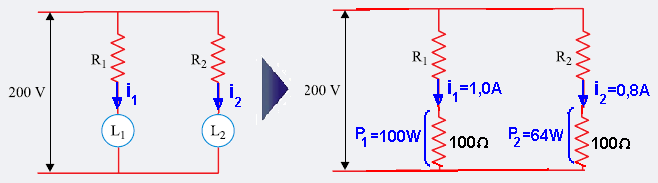
Observe na figura acima que a lâmpada L2 de resistência R=100 Ω, é percorrida por i2, e pelo enunciado sob potência de 64W, tal que — P2=R.i22 — 64=100. i12 — i2=0,8A. (corrente por L2 quando sob potência de 64W)
No trecho série R1 e L1 (R=100 Ω), percorridos por i1=1 A e sob ddp de U=200V (paralelos à fonte) você terá:
Req=(R1 + 100) — U=200V e i1=1 A — Req=U/i1 — R1 + 100 = 200/1 — R1=100 Ω.
No trecho série R2 e L2 (R=100 Ω), percorridos por i1=0,8 A e sob ddp de U=200V (paralelos à fonte) você terá:
Req=(R2 + 100) — U=200V e i2=0,8 A — Req=U/i2 — R2 + 100 = 200/0,8 — R2 + 100 = 250 —
R2=150 Ω.
Se R1 = 100 Ω, L1 dissipará uma potência de 100W e se R2 = 150 Ω, L2 dissipará uma potência de 64W,
conforme pedido no enunciado.
R- C
06- Você deve se lembrar de que a potência elétrica máxima que um gerador (no caso associação de geradores) fornece ao circuito externo (no caso, reostato R) ocorre quando a resistência externa R é igual à resistência interna r da associação de geradores, ou seja, quando R=requivalente — na associação série — requ=r + r=2r — R=2r — na associação paralelo — req=(r.r)/(r + r)=r/2 — req=r/2 — R=r/2 — veja na figura abaixo que a resposta corresponde à alternativa C:
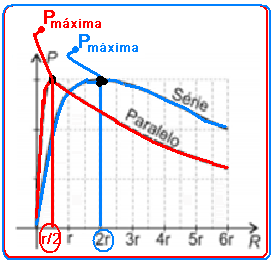
R- C
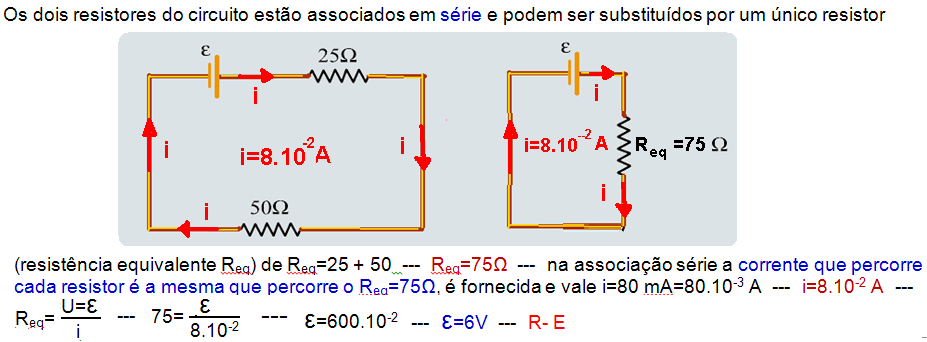
07- Associação série
Todos os resistores são ligados um em seguida ao outro.
A resistência equivalente (Req) é igual à soma das resistências parciais — no circuito 1 Req=R; no 2, Req=2R e no 3 Req=3R — a resistência equivalente da associação aumenta.
A tensão (diferença de potencial) U, constante, nos terminais da associação (entre A e B) é igual à soma das tensões em cada resistor, ou seja, no circuito 1 U1=U/1; no 2 U2=U/2 e no 3 U3=U/3 — a diferença de potencial nos extremos de um mesmo resistor diminui.
Pela lei de Ohm, como Req=U/i, a corrente elétrica i é inversamente proporcional à resistência equivalente Req, 0u seja, a medida que você acrescenta resistores, Req aumenta e, consequentemente i diminui.
R- E — Observação: Você poderia chegar à mesma conclusão observando a tabela fornecida e lembrando que, no caso, o voltímetro marca a ddp em cada resistor e o amperímetro a corrente total no circuito.
08- Cálculo da resistência equivalente Reqi antes de estabelecer o curto circuito:
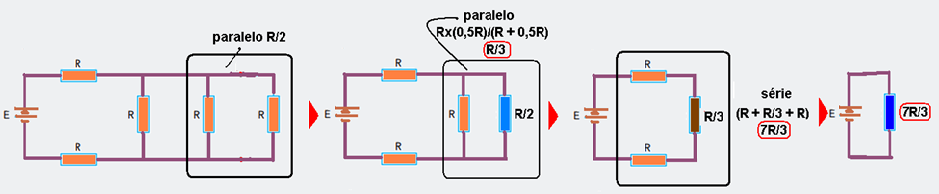
Reqi=7R/3 — Pi=U2/Reqi=E2/Reqi=E2/(7R/3) — Pi=3E2/7R (I)
Cálculo da resistência equivalente Reqf depois de estabelecer o curto circuito:
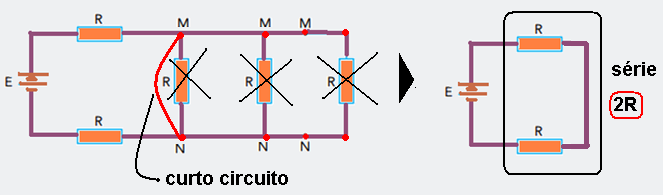
Reqf=2R — Pf=E2/Reqf — Pf=E2/2R (II)
(II)/(I) — Pf/Pi=(E2/2R)x(7R/3E2)=7/6
R- D
09- a) Observe no circuito que o resistor R e a lâmpada tipo led estão associados em série e uma das características da associação série é que a corrente elétrica que circula em cada aparelho é a mesma, ou seja, iℓ = iR — o enunciado fornece que a tensão (ddp) na lâmpada led é Uℓ=2,5V e, pelo gráfico, você
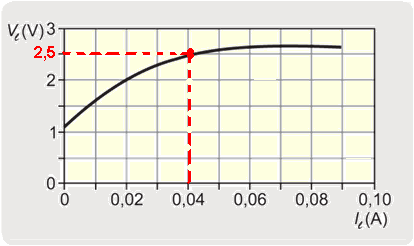
observa que iℓ=0,04 A — assim, iℓ = iR=0,04 A
b) Outra característica da associação série é que a tensão total (da bateria U=4,5V) é a soma das tensões
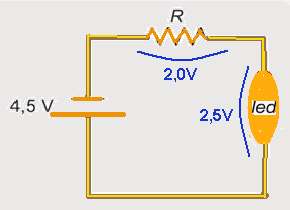
de cada elemento do circuito série — assim, U = Uℓ + UR — 4,5 = 2,5 + UR — UR=2,0V — R=UR/iR —
R=2/0,04 — R=50Ω
c) Corrente elétrica total i no circuito, agora com U=3V e R=50Ω pode ser determinada por P=i.U, onde P é fornecida P=60mW=60.10-3W — 60.10-3 = i.3 — i=60.10-3/3 — i=20.10-3 A — essa corrente é a mesma que flui pelo resistor R=50Ω (característica da associação série) — em R — P=R.i2=50.(20.10-3)2 50.400.10-6 — P=20000.10-6 =20.10-3 — P=20mW
10- Segunda lei de Ohm: Através de pesquisa, Ohm descobriu que a resistência elétrica de um condutor, mantida a temperatura constante, é diretamente proporcional ao comprimento L do fio, é inversamente proporcional à área de seção reta transversal S e depende do material que constitui o corpo (essa dependência do valor da resistência em relação ao material que constitui o resistor, chama-se resistividade do material e representa-se pela letra grega ρ “rô”).
Matematicamente:
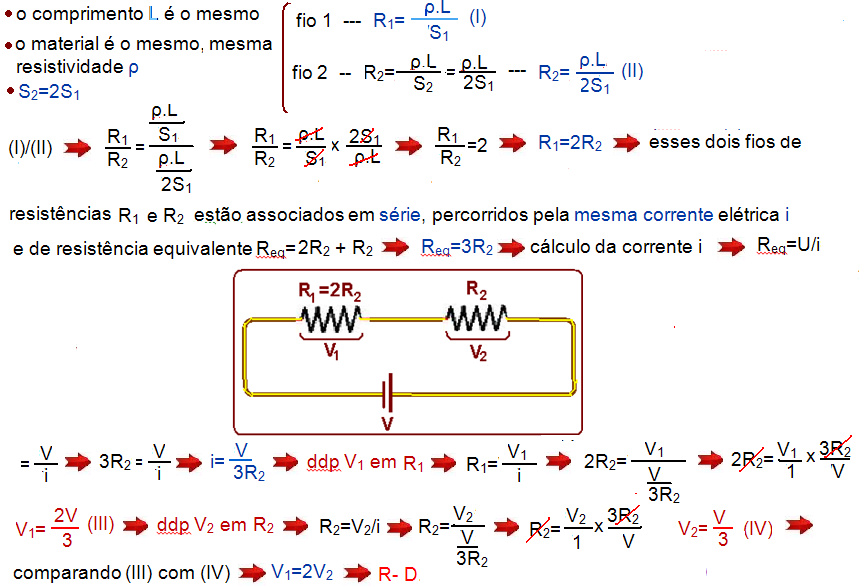
11- Da curva S do gráfico você pode calcular a resistência equivalente da associação série RS e da curva P do gráfico você pode calcular a resistência equivalente da associação série Rp:
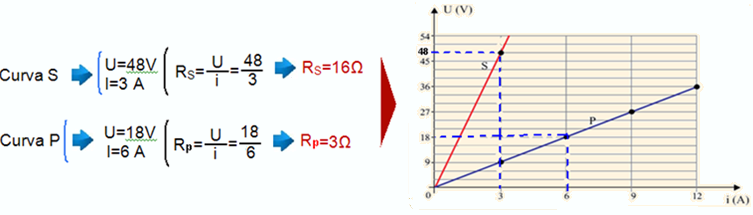
12-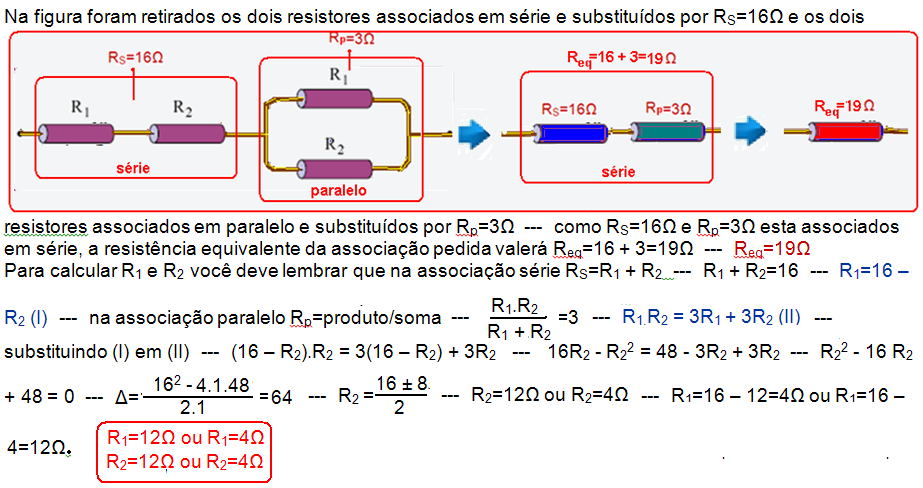 
12-
b) Inicialmente você deve determinar, utilizando o gráfico1, a intensidade do campo magnético H, sendo
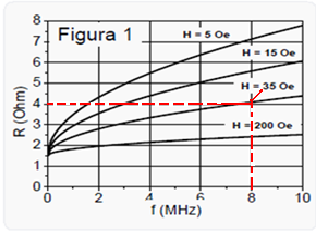
fornecido f=8MHz=8.106Hz e R≈4Ω — pelo gráfico — H=35Oe — em seguida, com esse valor
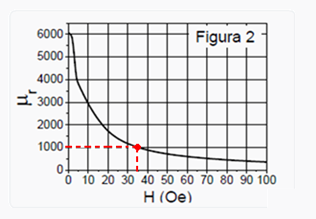
13- 04- Cálculo das resistências — R1=V1/i1=8/2=2Ω — R2=V2/i2=4/2=2Ω — R3=V3/i3=4/2=2Ω — R1=R2=R3.
Cálculo das potências — P1=i1.V1=4.8=32W — P2=i2.V2=2.4=8W — P3=i3.V3=2.4=8W — P1 > P23
R- D
14- Veja no circuito abaixo:
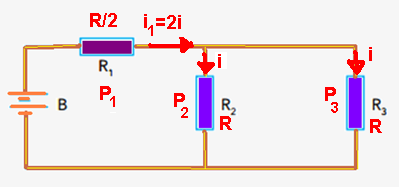
Relação entre P2 e P3:
Como R2=R3=R e, como eles estão em paralelo estão submetidos à mesma ddp (tensão) U eles são percorridos pela mesma corrente elétrica i2=i3=i — P2=R2.i22=R.i2 — P3=R3.i32=R.i2 — portanto P2=P3.
Potência em R1:
Pelo enunciado R1=R2/2=R3/2=R/2 — i1=i2 + i3=i + i=2i — P1=R1.i12=(R/2).(2i)2=(R/2)x4i2 — P1=
2Ri2 — mas, Ri2=P2=P3 — P1= 2P2= 2P3
R- D
15-
16- O voltímetro ideal (resistência interna infinita), associado corretamente (em paralelo às pilhas e à lâmpada) indica a ddp Ufornecida pelas duas pilhas à lâmpada que é fornecida — U=3,00V — o
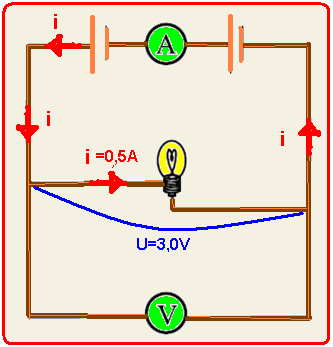
amperímetro ideal (resistência interna nula) indica a corrente elétrica i que circula pela lâmpada, também fornecida — i=0,50 A
— cálculo da potência P da lâmpada, que não é o valor nominal, nas condições do exercício — P=i.U=0,50×3,00 — P=1,50W — o enunciado afirma, sabe-se que a potência dissipada por efeito Joule no filamento da lâmpada corresponde a 1/4 do valor nominal Pn, indicado pelo fabricante, ou seja, P=Pn/4 —
Pn=4P=4×1,50 — Pn=6,0W — pela expressão Pn=Un2/R você observa que, sendo a resistência R da lâmpada a mesma, a potência nominal Pn é diretamente proporcional ao quadrado da tensão (ddp) nominal Un, ou seja, como a potência foi quadruplicada, a tensão deve ser dobrada, (2)2=4 para manter a igualdade — Un=2.3,00 — Un=6,0V
R- D
Corrente elétrica
37- Intervalo de tempo durante o qual a bateria está descarregando, até acabar, ou seja descarregar sua carga máxima que é de q=75 A.h — i=q/∆t — 75A.h = 50A/∆t — ∆t=75A.h/50A — ∆t=1,5h — supondo a velocidade de V=60km/h constante — V=∆S/∆t — 60=∆S/1,5 — ∆S=90,0km/h — R- C.
38- Deve funcionar assim, se um deles mantém a lâmpada acesa, o outro, quando acionado, deve apagá-la e vice versa, mantendo sempre o circuito fechado. Analise atentamente cada alternativa:
a) Falsa — tem apenas um fio ligado à rede elétrica externa o que impedirá a lâmpada de acender, não fechando o circuito, qualquer que seja a posição das chaves.
b) Falsa — a lâmpada está apagada — se você mudar a chave da esquerda ela continuará apagada — se você mudar a chave da direita ela continuará apagada — se você mudar as duas chaves, provocará um curto-circuito.
c) Falsa — a lâmpada está apagada — se você mudar a chaves da direita ou da esquerda ela continuará apagada.
d) Falsa — a lâmpada só acenderá com as duas chaves na posição superior — se você mudar uma delas, a outra não acenderá a lâmpada.
e) Correta — esse é o único caso em que você consegue acender ou apagar a lâmpada invertendo apenas uma das
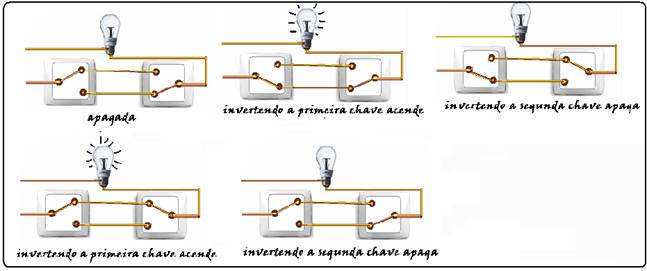
chaves, não importando a posição da outra.
R- E.
Potência elétrica – Energia elétrica
51- Em ∆t=2min=120s, a água recebeu Q=24000cal de energia térmica, que, em joules vale — regra de três — 1cal – 4J — 24000cal – W (J) — W=24000×4 — W=96000J — Potência elétrica do aquecedor — P=W/∆t=96000/120 — P=800W — P=U2/R — 800=1202/R — R=14400/800 — R=18Ω — pelo enunciado, em ∆t=2min=120s, a temperatura da água variou de 20°C a 80°C — ∆θ=(80 – 20)=60oC — equação fundamental da calorimetria — Q=m.c.∆θ — 24000=m.1.60 — m=400g — R- B.
52- Painel — Pp=Wp/24h — 810=Wp/24h — Wp=19440Wh (energia fornecida pelo painel em 1 dia) — energia dissipada pela lâmpada em 1 dia — Pl=Wl/24.∆t — 9=Wl/24.∆t — Wl=216.∆t (W) — Wp = Wl — 19440 = 216∆t — ∆t=90h — R- D.
53- a) Pelo enunciado observe que, para cada 100g de bauxita você tem 55g de óxido de alumínio (Al2O3) e 45g de resíduos — massa molar do óxido de alumínio (Al2O3) — 2x(27) + 3x(16)=102g.mol-1 — massa de alumínio que compõe o óxido de alumínio (alumina) — Al2=2x(27)= 54g.mol-1 — regra de três — 102g de Al2O3 – 54g de Al — 55g de Al2O3 – x — x=55×54/102 — x=29,12g de alumínio em 100g de bauxita — cálculo da massa de resíduos — regra de três — 29,12g de Al – 45g de resíduos — 32.106t de Al – y — y=45×32.106/29,12 — y=49,45t.106≈
4,9.107t de resíduos.
b) Dados — tempo de duração do banho — ∆t=10mim=10.60=600s — potência elétrica do chuveiro — P=3000W — P=energia(W)/ ∆t — 3000=W/600 — W=18.105J (energia dissipada num banho de 10min) — pelos dados, 1 latinha 3,6.106J — regra de três — 1 latinha – 3,6.106J — n latinhas – 18.106J — n=3,6.105/18.106=0,2.10 — n=2 banhos.
54- Pelo enunciado, a eficiência ε é fornecida pela razão entre a quantidade de luz produzida Q e a energia elétrica W consumida — ε =Q/W (I) — potência=energia/tempo de utilização — P=W/∆t — W=P.∆t (II) — substituindo (II) em (I) — ε =Q/P.∆t — para a lâmpada incandescente de 40W — ε’=600lm/40∆t — o intervalo de tempo ∆t é o mesmo para cada alternativa.
a) Falsa — lâmpada fluorescente de 8W — se uma lâmpada fluorescente de 40W emite Q=3000lm, uma de 8W emitirá 5 vezes menos, ou seja, Q=3000/5=600lm — ε=600lm/8∆t — observe que ε > ε’.
b) Falsa — lâmpada fluorescente de 40W — ε=3000lm/40∆t — observe que ε > ε’.
c) Verdadeira — lâmpada fluorescente de 8W — ε=600lm/8∆t — ε’ < ε e mesmo Q=600lm.
d) Falsa — veja (b).
e) Falsa — veja (B).
R- C.
Resistores – Primeira lei de Ohm – Potência elétrica em um resistor
47- Resistência elétrica de um resistor – representa a medida da dificuldade imposta à movimentação das cargas elétrica que o atravessam (corrente elétrica), e é definida como a razão entre a diferença de potencial (U) nos terminais do resistor e a intensidade da corrente elétrica ( i ) que o atravessa:
A expressão acima é conhecida como Lei de Ohm
Um ohm (1Ω) é o valor da resistência elétrica entre dois pontos P e Q de um condutor quando, sob diferença de potencial de 1 volt
(1V) é percorrido por uma corrente elétrica constante de 1 ampère (1A).
Representação simbólica:
Primeira lei de Ohm – Se a resistência elétrica de um resistor for constante, a diferença de potencial aplicada nos seus extremos é diretamente proporcional à intensidade da corrente elétrica, ou seja,U1/i1=U2/i2= . . . =U/i=constante. Nesse caso eles são chamados de resistores (ou condutores) ôhmicos e, como a relação R=U/i é uma função do primeiro grau o gráfico U x i tem o aspecto do gráfico da esquerda da figura abaixo:
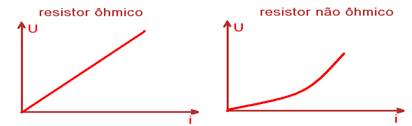
Qualquer gráfico U x i diferente do gráfico da esquerda da figura acima não representa um resistor ôhmico, como por exemplo, o gráfico da direita.
R- A.
48- Corrente que provoca fibrilação ventricular passando pelo tórax — iv=500mA=500.10-3=0,5 A — corrente provocada pelo poraquê de U=1500Vquando o pescador o segura com uma mão na cabeça e outra na cauda e que passa pelo seu tórax de R=1000Ω — R=U/i — 1000=1500/i — i=1500/1000 — i=1,5 A — relação entre essas correntes — i/iv=1,5/0,5 — i=3iv — R- E.
49- A) Na posição INVERNO o chuveiro deve dissipar a maior potência (4800W) — como a ddp (tensão) U é constante, pela expressão P=U2/R você observa que a potência P é inversamente proporcional à resistência elétrica R e,
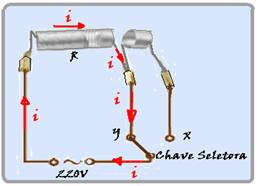
assim para uma maior potência corresponde uma menor resistência elétrica, o que ocorre quando a chave seletora estiver ligada na posição Y.
B) Na posição INVERNO a potência deve ser P=4800W — ∆t=10min=10/60=1/6h — P=W/∆t — 4800=W/(1/6) — W=0,8kWh.
C) Uma pessoa num dia — P=0,8kWh — 4 pessoas num dia — P=3,2kWh — 4 pessoas num mês — P=3,2×30 = 96kWh — como a residência consome num mês 200kWh, sem os banhos a economia será de W’=200 – 96=104kWh.
50- Num chuveiro elétrico, normalmente de tensão 220V (mantida constante), as posições inverno (quente), verão (morna) correspondem à diferentes potências. Quando você muda o cursor do chuveiro, por exemplo, do verão para
o inverno, você está diminuindo a resistência elétrica no interior do chuveiro e, consequentemente aumentando a potência, fazendo-o aquecer mais, claro que mantendo a vazão constante. O oposto ocorre quando você muda o cursor do chuveiro do inverno para o verão. Isso acontece porque, para a mesma tensão, a potência é inversamente proporcional à resistência, pois, P=U2/R, com U constante.
R- D.
51- O condutor possui resistência ôhmica, pois o gráfico é uma reta inclinada a partir da origem e a ddp U é diretamente proporcional a i de modo que R seja constante — R= U/i= 20/0,5 = 40/1 = 60/1,5 = 80/2=40Ω — P=R.i2=40.(1,5)2 P=40.2,25 — P=90W — R- C.
52- O funcionamento do fusível baseia-se no princípio segundo o qual uma corrente que passa por um condutor gera calor proporcional ao quadrado de sua intensidade — quando a corrente atinge a intensidade máxima tolerável, o calor gerado não se dissipa com rapidez suficiente, derretendo um componente e interrompendo o circuito.
Disjuntores — modernamente, nos circuitos elétricos de residências, edifícios e indústrias, em vez de fusíveis, utilizam-se dispositivos baseados no efeito magnético da corrente denominados disjuntores — em essência, o disjuntor é uma chave magnética que se desliga automaticamente quando a intensidade da corrente no condutor supera certo valor — tem sobre o fusível a vantagem de não precisar ser trocado — uma vez resolvido o problema que provocou o desligamento, basta religá-lo para que a circulação da corrente se restabeleça — R- D.
Segunda lei de Ohm (Resistividade)
33- U=270V — l=1,5m — ρ=1,8Ωm — S=30cm2=30.10-4=3.10-3m3 — R=ρ.l/S=1,8.1,5/3.10-3 — R=900Ω — R=U/i — 900=270/i — i=270/900=0,3 A=300mA — a corrente elétrica fatal é de 200mA — R- E.
34- Segunda lei de Ohm — R=ρℓ/S=1,8.10-9.3.105/2.10-4=1,8.1,5.10o — R=2,7Ω — R- D.
Resistor equivalente nas associações série, paralelo e mista – curto circuito
49- Série — Req=2R — Req=U/i1 — 2R=U/i1 — i1=U/2R — paralelo — Req=R/2 — R/2=U/i2 — i2=2U/R — i2 – i1 = 9 — 2U/R – U/2R=9 — 3U/2R=9 — 3.60/2R=9 — R=10Ω — R- D.
50- Pelo enunciado A’A=R1 e B’B=R2 — denominando AP’ de m e P’B de n e observando que os
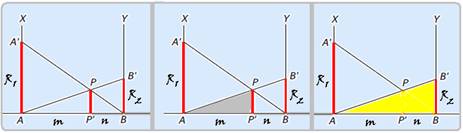
triângulos nas figuras são semelhantes — P’P/R2=m/(m + n) (I) — os dois triângulos hachurados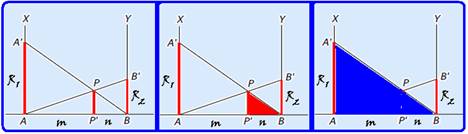 
nas figuras a seguir também hachurados são semelhantes — P’P/R1=n/(m + n) (II) — (I) + (II) — P’P/R2 + P’P/R1 = m/(m + n) + n/(m + n)=(m + n)/(m + n)=1 — P’P/R2 + P’P/R1=1 — P’P.R1 + P’P.R2=R1.R2 — P’P=R1.R2/(R1 + R2).
Características de associação série e associação paralela
60- Série — Req=2R — Req=U/i1 — 2R=U/i1 — i1=U/2R — paralelo — Req=R/2 — R/2=U/i2 — i2=2U/R — i2 – i1 = 9 — 2U/R – U/2R=9 — 3U/2R=9 — 3.60/2R=9 — R=10Ω — R- D.
61- Como as lâmpadas estão associadas em paralelo, a tensão U é a mesma para cada lâmpada e vale U=120V — potência de cada lâmpada P=60W — corrente i em cada lâmpada — P=i.U — 60=i.120 — i=0,5 A — a corrente limite do fusível (corrente total de entrada) deve ser de it=10 A — essa corrente é dividida em n lâmpadas cada uma com 0,5 A — it=n.i — 10=n.0,5 — n=20 lâmpadas — R- C.
62- O mesmo aquecimento corresponde à mesma quantidade de energia, assim, Wparalelo=Wsérie — P=W/∆t — W=P.∆t — Wp = Ws — Pp.∆tp = Ps.∆ts — P=U2/R (U constante, dado do exercício) — (U2/Rp).∆tp = (U2/Rs),∆ts — ∆tp/Rp=∆ts/Rs — associação paralelo Req=Rp=R/2 — associação série Req=Rs=2R — ∆tp/(R/2) = ∆ts/2R — ∆tp = ∆ts/4 — ∆ts=1min=60s — ∆tp=60/4=15s — R- E.
63- Pelo enunciado, se o acerto é zero, somente a chave C é fechada e o circuito fica conforme a
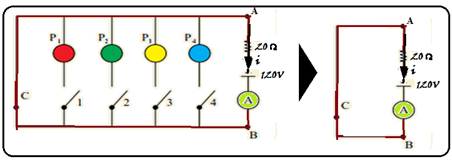
figura — o amperímetro indica a corrente no circuito de valor — R=U/i — 20=120/i — i=6 A — se o participante errar apenas P2, não passará corrente por ela e a corrente circulará apenas nas lâmpadas P1, P3 e P4, com a chave C aberta
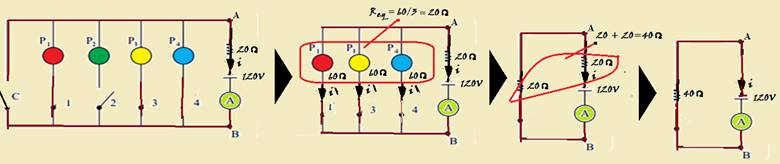
— veja a sequência indicada na figura acima onde a resistência equivalente vale Req=40Ω — Req=U/i — 40=120/i — i=3 A.
64- Cálculo da resistência equivalente para as 25 lâmpadas, cada uma com resistência R associadas em série (i é a mesma e a resistência equivalente é a soma da resistência de todas as lâmpadas em série) — Reqs=25R — na associação em paralelo que fornece a resistência equivalente total (Reqtotal), você tem 4 resistência de 25R associadas em paralelo — 1/Reqtotal= 1/25R + 1/25R + 1/25R + 1/25R=4/25R — Reqtotal=25R/4 (I) — cálculo da resistência equivalente total pelos valores nominais fornecidos (potência elétrica e tensão totais) — P=U2/Reqtotal — 22 = 2202/Reqtotal — Reqtotal=48400/22 — Reqtotal=2200Ω (II) — igualando (I) com (II) — 25R/4 = 2200 — R=8800/25=352Ω —
R- C.
65- a) Estando esses aparelhos funcionando normalmente, todos eles estão submetidos à mesma ddp (tensão) que é de U-110V e, para que isso ocorra, todos esses aparelhos devem estar associados em paralelo.
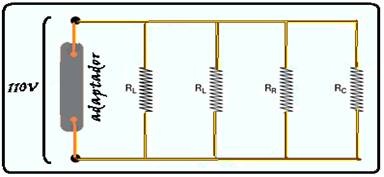
Como todos os aparelhos estão funcionando dentro das especificações comerciais, a potência total dissipada é a soma da potência de cada um desses aparelhos — Ptotal=40 + 40 + 20 + 120=220W — Ptotal=itotal..U — 220= itotal.110 —
itotal=2 A.
b) Tempo de funcionamento — ∆t=30diasx4h=120h — Ptotal=W/∆t — 220W=W/120h — W=26400W=26,4kWh — custo — C$=26,4×0,30=7,92 — C$=7,92 reais.
Cálculo de correntes, tensões e potências em associações mistas
42- Um voltímetro ideal (resistência interna infinita) inserido na entrada indicaria — Ventrada =Req.i=(R1 + R2).i — um
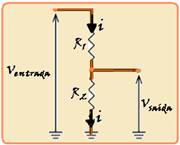
voltímetro ideal (resistência interna infinita) inserido na saída indicaria — Vsaída =Req.i=R2.i — pelo enunciado Vsaída=
Ventrada/10 — R2.i = (R1 + R2).i/10 — 10R2=R1 + R2 — 9R2=R1 — R1/R2=9.
43-
R- C.
44- Observe que entre os pontos P (de potencial +5V) e A você tem o resistor de 4kΩ em circuito aberto e que, nesse trecho não passa corrente — assim, o potencial no ponto A é o mesmo que no ponto P e vale +5V — observe também que os dois resistores de 2kΩ estão em paralelo e devem ser substituídos por um único de Req=produto/soma=(2×2)/(2 + 2) — Req=1kΩ — haverá passagem de corrente elétrica apenas nos trechos PBQ (veja
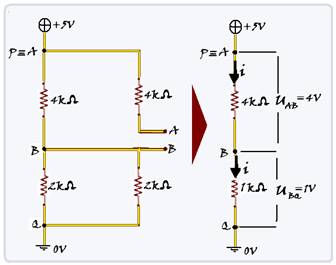
figura) e nele os resistores de 4kΩ e 1kΩ estão em série, sobrando apenas um resistor de R=4 + 1=5kΩ submetido a uma ddp de U=(5 – 0)=5V — R=U/i — 5.103 = 5/i — i=5/5.103 — i=1.10-3 A ou i=1m A — entre A e B — RAB=UAB/i — 4.103=UAB/10-3 — UAB=4.103.10-3 — UAB=4V — entre B e Q — RBQ=UBQ/i — 1.103=UBQ/10-3 — UBQ=1.103.10-3 — UBQ=1V — R- B.
Geradores – associação de geradores
48- Observe na sequência abaixo o cálculo do resistor equivalente de resistência Req=10Ω e da
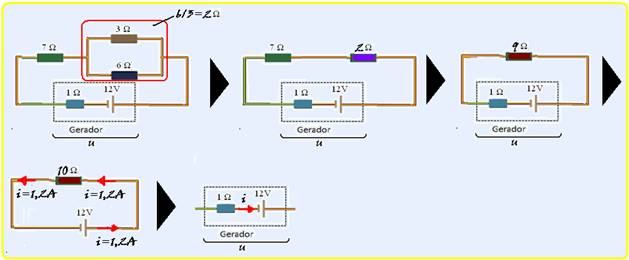
corrente total i — Req=ε /i — 10=12/i — i=1,2 A — cálculo da diferença de potencial U nos terminais do gerador de resistência interna r=1Ω — Usando a equação do gerador — U= ε – r.i=12 – 1.1,2 — U=10,8V — R- C.
49- Corrente i no motor de equação U=E’ + r’.i — 1,2=1,0 + 0,2i — i=1 A — tempo que ele demora
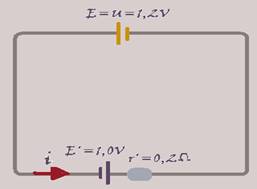
para dissipar a carga Q=1200mAh=1,2Ah fornecida pelo motor — i=Q/t — 1A = 1,2Ah/∆t — ∆t=1,2h — R- C.
50- A ligação em paralelo obtida quando se liga entre si todos os pólos positivos dos geradores (o terminal da união é o de mais alta tensão do circuito) e todos os pólos negativos (o terminal de união é o de mais baixa tensão do circuito). Nesse tipo de associação convém que todos os geradores tenham a mesma força eletromotriz E, para que não dissipem parte da energia que fornecem ao circuito externo.
Características desse tipo de associação:
A intensidade de corrente elétrica se subdivide entre os geradores
A força eletromotriz da associação é igual àquela de cada um dos geradores — Eeq=E
Observe que, quando você liga as duas baterias do exercício em paralelo (figura I) a tensão do sistema é a mesma que a da bateria carregada — R- D.
51- a) Utilizando a primeira lei de Ohm (R=V/i) você pode completar a tabela — quando V=1,10V e R=4,40Ω — 4,40 = 1,10/i — i=0,25 A — quando V=0,96V e R=1,60Ω — 1,60 =0,96/i — i=0,60 A.
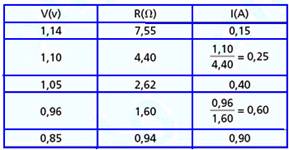
b) Construindo o gráfico a partir dos valores da tabela:
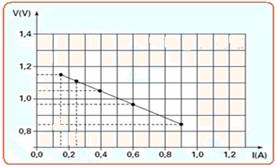
c) Você pode obter a força eletromotriz do gerador, prolongando a reta representativa até tocar o eixo das tensões —
este ponto fornece a força eletromotriz ε que no caso é aproximadamente de ε≈1,20V — a resistência interna r pode ser determinada pela equação do gerador — V = E – r.i — quando, por exemplo V=0,96V, i=0,6 A — 0,96 = 1,2 – r.0,6 — r≈0,4Ω.
Circuitos com geradores
29- a) Observe na seqüência abaixo o cálculo da resistência do resistor equivalente (Req) —
Req=U/i — 4,5.103=12/i — i=12/4,5.103 — i=2,7.10-3A=2,7mA.
b) Observe na figura abaixo os valores das correntes devidamente distribuídas — entre os pontos B
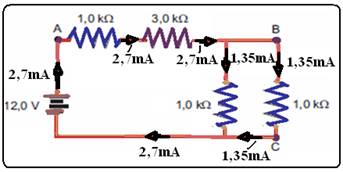
e C, R=1kΩ e i=1,35.10-3 A — R=U/i — 1.103=U/1,35.10-3 — U=1,35.10-3.103 — U=1,35V.
30- Observe na sequência abaixo o cálculo da resistência do resistor equivalente — Req=U/i —
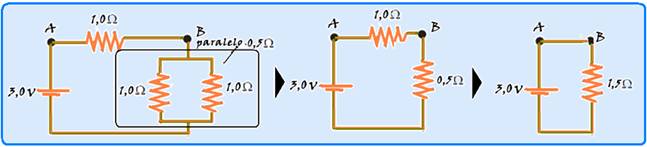
1,5=3/i — i=2A —entre os pontos A e B flui uma corrente i=2A na resistência de R=1Ω — R=UAB/i — UAB=1.2=2V — R- C.
31- Cálculo da corrente elétrica i que percorre o resistor de 4Ω quando dissipa uma potência de 36W — P=R.i2 — 36=4.i2 — i=3A — observe que a resistência equivalente (Req) é percorrida pela corrente i=3A quando submetida à ddp (tensão) de U=24V — Req=U/i=24/3=8Ω — observe na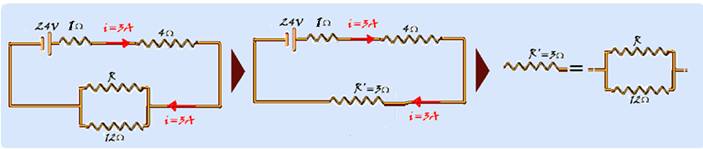 
sequência abaixo que, como Req=8Ω, a resistência R’ (que corresponde a R associado em paralelo com 12Ω) deve valer R’=8 – (1 + 4) =3Ω — 3=produto/soma=12R/(12 + R) — 3=12R/(12 + R) — 36 + 3R=12R — 9R=36 — R=4Ω — R- B.
Receptores e associação de geradores e de receptores
30- Equação do receptor — U=E’ + r.i — pelo gráfico — quando U=45V, i=8 A — 45=E’ + r.8 (I) — quando U=40V, i=3 A — 40=E’ + r.3 (II) — multiplicando (II) por (-1) e somando com (I) — 5=5r — r=1Ω — subst. Em (I) — 45=E’ + 1.8 — E’=37V — R- A.
31- A) A tensão U que a bateria de fem E e resistência interna r fornece ao circuito externoé dada pela equação do gerador — U=E – r.i — do gráfico — quando U=10V, i=4 A — 10=E – r.4 (I) — quando U=8V, i=8 A — 8=E – r.8 (II) — resolvendo (I) com (II) — E=12V e r=0,5Ω.
B) Calculado em (A) — r=0,5Ω.
C) Para essa particular lâmpada a corrente I=6,0A — U=12 – 0,5.6=12 – 3=9V — R=9/6=1,5Ω.
D) Potência dessa particular lâmpada de R=1,5Ω e I=6 A — P=R.I2=1,5.36 — P=54W — o rendimento do gerador (bateria) é fornecido por η=Pútil/Ptotal=Ui/Ei=9/12=0,0,75 — η=75%
Aparelhos de medição elétrica (amperímetros, voltímetros, ponte de Wheatstone)
36- Se você não domina a teoria, leia as informações a seguir:
Ponte de Wheatstone – trata-se de uma associação de três resistores fixos e um variável (reostato), como representado na figura.
Serve, dentre outras coisas, para determinar a resistência de um resistor. Conhecendo, por exemplo, R1, R2 e R4, pode-se determinar R3, da seguinte maneira:
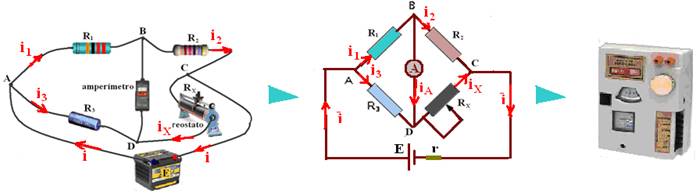
Liga-se entre B e D um amperímetro muito sensível (galvanômetro)
Varia-se o reostato (resistência variável) RX até que a intensidade iA de corrente no amperímetro se torne nula (iA=0). Nessa situação, diz-se que a ponte está em equilíbrio. Sendo nula a corrente no amperímetro, não existe diferença de potencial entre os pontos B e D.
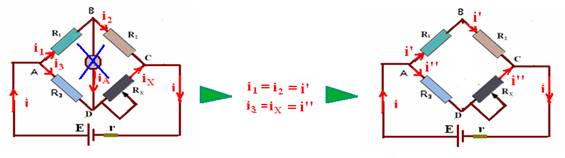
UAB=UAD — R1.i1=R3.i3 (I) — UBC=UCD — R2.i2=RX.iX (II) — Dividindo membro a membro (I) por (II) — (R1.i1)/(R2.i2)=(R3.i3)/(RX.iX) — R1.i’)/(R2.i’)=(R3.i’’)/(RX.i’’) — R1/R2=R3/RX — R2.R3=R1.RX
Observe no circuito fornecido que, como as lâmpadas são idêntica, possuem a mesma resistência R — RI.RV=RII.RIV — assim, trata-se de uma ponte de Wheatstone em equilíbrio e pela lâmpada de resistência RIII não passa corrente elétrica — R- C.
37- Os aparelhos estão ligados corretamente — o amperímetro em série e o voltímetro em paralelo — considerando os aparelhos ideais, se o amperímetro estivesse ligado em paralelo você teria um curto circuito e, se o voltímetro estivesse ligado em série não passaria corrente pelo condutor — o resistor não é ôhmico, pois R=U/i não é constante para todas as medidas — R- D.
38- Se você quer medir a intensidade da corrente, por exemplo, em uma lâmpada, você deve inserir o amperímetro no trecho onde ela está, pois ele “lê” a corrente que passa através dele — assim o amperímetro deve ser associado em série no trecho onde você deseja medir a corrente — R- A.
Capacitores – condensadores
52- Série — 1/Ceq=1/C + 1/C + 1/C — 2p=C/3 — C=6p — paralelo — Ceq=6p + 6p=12pF —
R- C.
53- Na seqüência abaixo, em (I) foi calculada a capacitância equivalente de cada linha (associadas em série) e calculadas por 1/Ceq=1/C + 1/C + 1/C + 1/C, cujos valores estão fornecidos em (II) — em (II) eles estão associados em paralelo
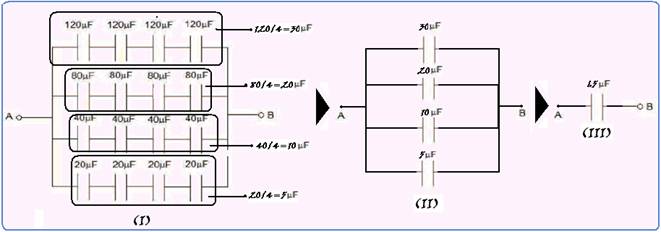
(Ceq=30 + 20 + 10 + 5=65 μF) — Ceq= 65 μF — a energia elétrica acumulada entre os terminais é fornecida por — W=Ceq.U2/2=65.10-6.5002/2=8125000.10-6J — W=8,125J — R- B.
54- Observe na seqüência a seguir o cálculo do capacitor equivalente (Ceq) — C1 e C2 estão em
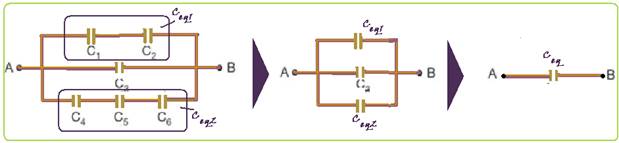
série — Ceq1=20.30/(20 + 30) — Ceq1=600/50=12μF — C4, C5 e C6 estão em série — 1/Ceq2=1/40 + 1/50 + 1/60=(15 + 12 + 10)/600 — Ceq2=600/37=16,2μF — Ceq1, C2 e Ceq2 estão em paralelo — Ceq=12 + 16,2 + 10= 38,2μF — Ceq=Q/U — 38,2.10-6 =Q/110 — Q=4202μC — R- B.