FUVEST 2020 – 2a fase
FUVEST – 2020 – Segunda Fase
Compare essa e outras resoluções da FUVEST- 2020 – Segunda fase com as dos vestibulares das demais Universidades pelo fisicaevestibular.com.br com outras e você verá que ela:
Tem melhor visual e mais ilustrações esclarecedoras.
Foi feito para alunos que realmente tenham dificuldades nos conceitos de Física e Matemática procurando sempre explicar os menores detalhes.
Não coloca apenas as fórmulas procurando sempre mostrar suas procedências e utilidades.
Sempre que preciso procura explicar por meio de desenhos e ilustrações.
Não queima etapas explicando sequência por sequência.
A preocupação com que o aluno entenda as resoluções é muito grande. O professor se coloca no lugar do aluno.
Muitas vezes fornece informações além das necessárias para as resoluções, mas úteis nos próximos vestibulares.
E muito, muito mais.
A Universidade de São Paulo (USP) é uma das três universidades públicas mantidas pelo governo do estado brasileiro de São Paulo, junto com a Universidade Estadual de Campinas (Unicamp) e a Universidade Estadual Paulista (UNESP). É a maior universidade pública brasileira, bem como uma das universidades mais prestigiadas do país. A USP é uma das maiores instituições de ensino superior naAmérica Latina, com aproximadamente 88 000 alunos matriculados. Ela possui doze campi, quatro deles em São Paulo (o campus principal é chamado Cidade Universitária Armando de Salles Oliveira, com uma área de 7 443 770 m²). Há campi nas cidades de Bauru, Lorena, Piracicaba, Pirassununga, Santos, Ribeirão Preto e dois em São Carlos. A USP está envolvida no ensino, pesquisa e extensão universitária em todas as áreas do conhecimento.
Segundo o relatório mundial de 2012 (SIR World Report) da SCImago Institutions Rankings, a USP está classificada na décima primeira posição mundial entre as 3 290 instituições de ensino e pesquisa internacionais classificadas. No ano de 2012, de acordo com o University Ranking by Academic Performance (URAP), a USP continua sendo a melhor universidade iberoamericana e está colocada na vigésima oitava posição no mundo.
A principal forma de ingresso é o vestibular da Fuvest
01- (FUVEST- SP- 2020 – Segunda Fase)
Uma pessoa produz oscilações periódicas em uma longa corda formada por duas porções de materiais diferentes 1 e 2, nos quais a velocidade de propagação das ondas é, respectivamente, de 5 m/s e 4 m/s.
Segurando a extremidade feita do material 1, a pessoa abaixa e levanta sua mão regularmente, completando um ciclo a cada 0,5 s, de modo que as ondas propagam‐se do material 1 para o material 2, conforme mostrado na figura.
Despreze eventuais efeitos de reflexão das ondas.
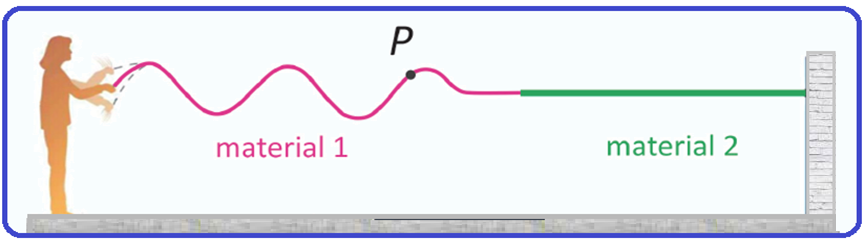
a) Circule, dentre os vetores na folha de respostas, aquele que melhor representa a velocidade do ponto P da corda no instante mostrado na figura.
b) Calcule a frequência e o comprimento de onda no material 1.
c) Calcule a frequência e o comprimento de onda no material 2.
02- (FUVEST- SP- 2020 – Segunda Fase)
03- (FUVEST- SP- 2020 – Segunda Fase)
A tomografia por emissão de pósitrons (PET) é uma técnica de imagem por contraste na qual se
utilizam marcadores com radionuclídeos emissores de pósitrons.
O radionuclídeo mais utilizado em PET é o isótopo 18 do flúor, que decai para um núcleo de oxigênio‐18, emitindo um pósitron.
O número de isótopos de flúor‐18 decai de forma exponencial, com um tempo de meia vida de aproximadamente 110 minutos.
A imagem obtida pela técnica de PET é decorrente da detecção de dois fótons emitidos em sentidos opostos devido à aniquilação, por um elétron, do pósitron resultante do decaimento.
A detecção é feita por um conjunto de detectores montados num arranjo radial.
Ao colidir com um dos detectores, o fóton gera cargas no material do detector, as quais, por sua
vez, resultam em um sinal elétrico registrado no computador do equipamento de tomografia.
A intensidade do sinal é proporcional ao número de núcleos de flúor‐18 existentes no início do processo.
a) Após a realização de uma imagem PET, o médico percebeu um problema no funcionamento do equipamento e o reparo durou 3h 40min. Calcule a razão entre a intensidade do sinal da imagem obtida após o reparo do equipamento e a da primeira imagem.
b) Calcule a energia de cada fóton gerado pelo processo de aniquilação elétron‐pósitron considerando que o pósitron e o elétron estejam praticamente em repouso.
Esta é a energia mínima possível para esse fóton.
c) A carga elétrica gerada dentro do material do detector pela absorção do fóton é proporcional à energia desse fóton.
Sabendo‐se que é necessária a energia de 3 eV para gerar o equivalente à carga de um elétron no material, estime a carga total gerada quando um fóton de energia 600 keV incide no detector
04- (FUVEST- SP- 2020 – Segunda Fase)
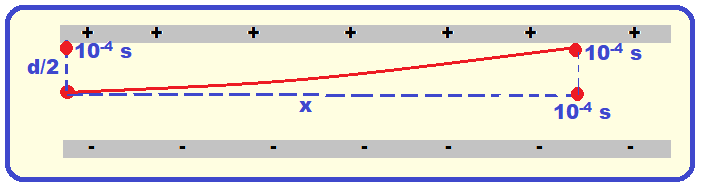
Em um ambiente do qual se retirou praticamente todo o ar, as placas de um capacitor estão arranjadas paralelamente e carregadas com cargas de mesma magnitude Q e sinais contrários, produzindo, na região entre as placas, um campo elétrico que pode ser considerado uniforme, com módulo igual a 106 V/m.
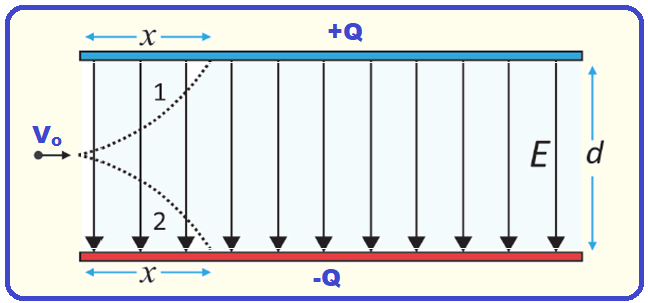
Uma partícula carregada negativamente, com carga de módulo igual a 10-9 C é lançada com velocidade de módulo Vo = 100 m/s ao longo da linha que passa exatamente pelo centro da região entre as placas, como mostrado na figura.
A distância d entre as placas é igual a 1 mm.
Despreze os efeitos gravitacionais.
a) Aponte, entre as trajetórias 1 e 2 mostradas na figura, aquela que mais se aproxima do movimento da partícula na região entre as placas.
b) Sabendo que a massa da partícula é igual a 10 μg, determine a que distância horizontal x a partícula atingirá uma das placas, supondo que elas sejam suficientemente longas.
c) Quais seriam o sentido e o módulo de um eventual campo magnético a ser aplicado na região entre as placas, perpendicularmente ao plano da página, para que a partícula, em vez de seguir uma trajetória curva, permaneça movendo-se na mesma direção e no mesmo sentido com que foi lançada?
05- (FUVEST- SP- 2020 – Segunda Fase)
Em janeiro de 2019, a sonda chinesa Chang’e 4 fez o primeiro pouso suave de um objeto terrestre no lado oculto da Lua, reavivando a discussão internacional sobre programas de exploração lunar.
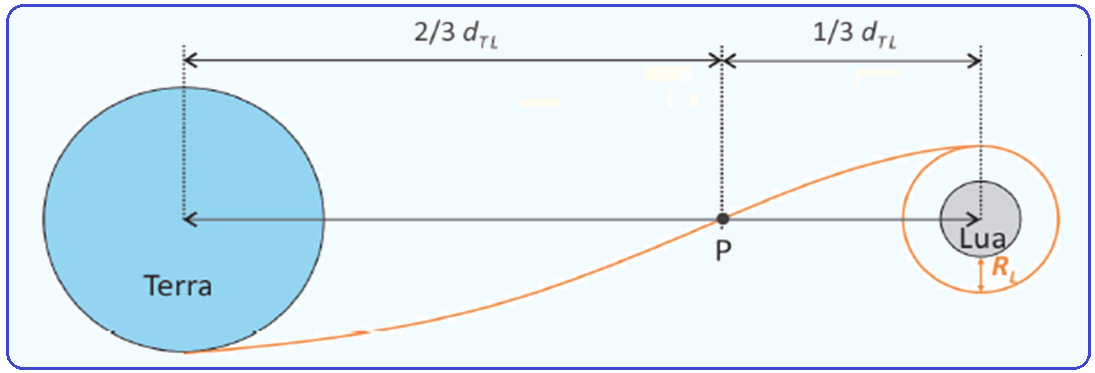
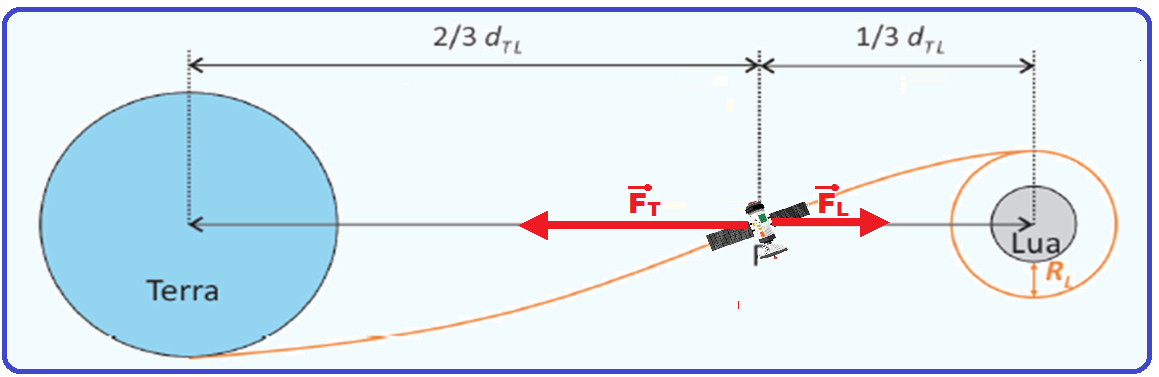
Considere que a trajetória de uma sonda com destino à Lua passa por um ponto P, localizado a
do centro da Terra e a 
do centro da Lua, sendo 
a distância entre os centros da Terra e da Lua.
a) Considerando que a massa da Terra é cerca de 82 vezes maior que a massa da Lua, determine a razão 
entre os módulos da força gravitacional que a Terra e a Lua, respectivamente, exercem sobre a sonda no ponto P.
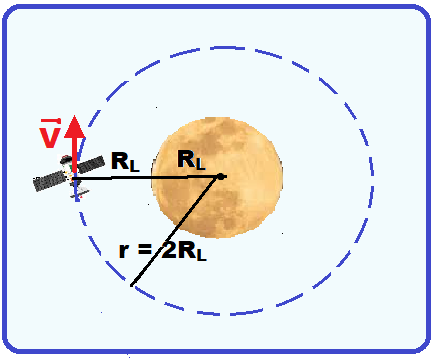
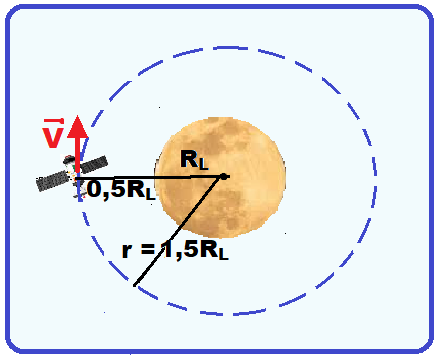
Ao chegar próximo à Lua, a sonda foi colocada em uma órbita lunar circular a uma altura igual ao raio da Lua 
, acima de sua superfície, como mostra a figura.
Desprezando os efeitos da força gravitacional da Terra e de outros corpos celestes ao longo da órbita da sonda,
06- (FUVEST- SP- 2020 – Segunda Fase)
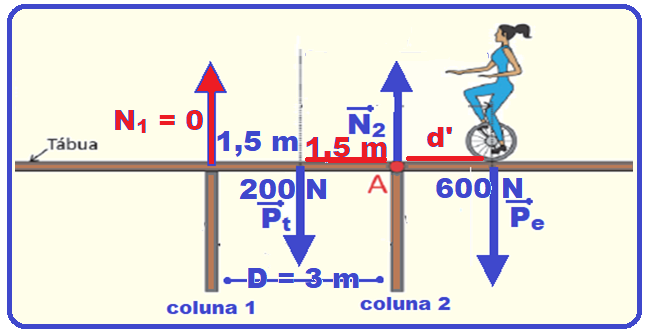
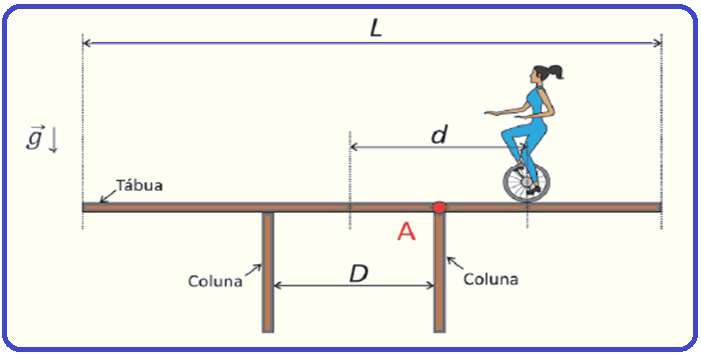
Uma equilibrista de massa M desloca‐se sobre uma tábua uniforme de comprimento L e massa m apoiada (sem fixação) sobre duas colunas separadas por uma distância D (D < L) de modo que o centro da tábua esteja equidistante das colunas.
O ponto de apoio da equilibrista está a uma distância d (tal que D/2 < d < L/2) do centro da tábua, como mostra a figura.
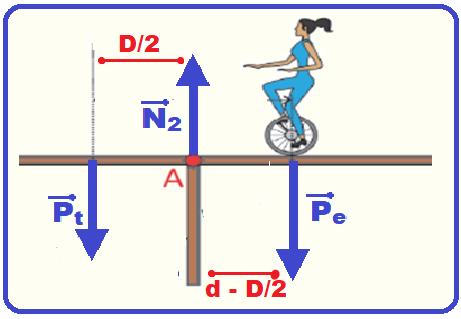
a) Considerando que a tábua está em equilíbrio, faça um diagrama indicando todas as forças que atuam sobre a tábua e seus respectivos pontos de aplicação.
b) Calcule o torque resultante exercido pelos pesos da equilibrista e da tábua em relação ao ponto A (ponto de apoio da tábua na coluna mais próxima da equilibrista).
Escreva sua resposta em termos de grandezas mencionadas no enunciado (M, L, m, D, d) e da aceleração da gravidade g.
c) Calcule a distância máxima 
da equilibrista ao centro da tábua para que o conjunto permaneça em equilíbrio estático.
Considere os seguintes dados: comprimento da tábua: L = 5 m; massa da tábua: m = 20 kg, massa da equilibrista: M = 60 kg, distância entre as colunas: D = 3 m.
Resolução comentada das questões de Física do vestibular da FUVEST – SP – 2020 – Segunda Fase
01-
a)
Vetores fornecidos na folha de resposta
Representação da direção e sentido da velocidade 
de propagação de um ponto numa corda em uma onda transversal
Observe que o ponto P do exercício está localizado na região do ponto A da figura acima e deve ter direção vertical e sentido para baixo. Assim, o vetor que você deve circular está representado abaixo.
b) A frequência f com que uma onda está se propagando independe do meio de propagação e é sempre a mesma que a da fonte que a está emitindo no caso é a mesma que a da mão cujo período T é fornecido (T = 0,5 s, completa um ciclo a cada 0,5 s).
02-
a)
Transformação adiabática
Exemplo prático
Na figura abaixo, trata-se de uma expansão adiabática (muito rápida e sem troca de calor com o meio
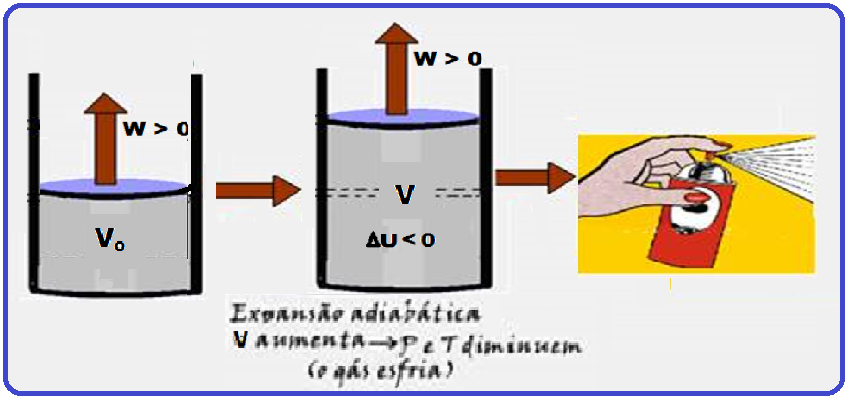
b)
03-
a)
Do note e adote “Tempo de meia vida”: tempo necessário para que o número de núcleos radioativos caia pela metade do valor inicial.
b)
c)
04-
a) A partícula que é lançada ao longo da linha que passa exatamente pelo centro da região entre as placas tem carga negativa e como cargas de mesmo sinal se repelem e de sinais opostos se atraem
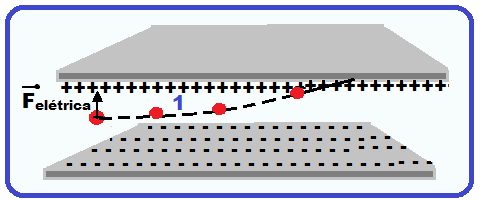
ela é atraída pela placa positiva (cima) e, ao mesmo tempo repelida pela placa negativa (baixo) recebendo uma força elétrica para cima e se deslocando conforme a trajetória 1.
b) O movimento da carga elétrica de módulo q entre as placas deve ser decomposto em duas direções: vertical v e horizontal h.
Força magnética sobre uma carga móvel imersa num campo magnético
Quando uma carga elétrica que se move com velocidade 
no interior de um campo magnético 
sobre ela surge uma força de origem magnética 
( denominada força de Lorentz), com as seguintes características:
Direção e sentido de 
fornecidos pela regra da mão esquerda conforme mostrado na
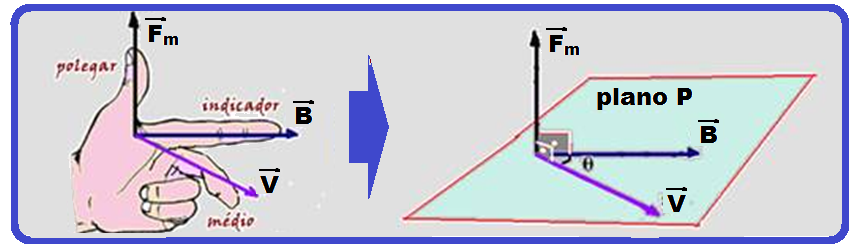
figura acima.
Observe na figura da direita que é perpendicular a e a , o que impõe a condição de que e devem pertencer a um mesmo plano.
Observe também que θ é o ângulo entre e .
Observação: Se q for negativa você deve inverter o sentido da força magnética
Veja a aplicação da regra da mão esquerda na sequência de figuras abaixo onde, na aplicação
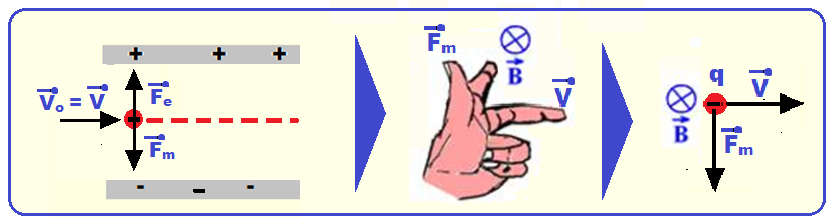
da mão esquerda o sentido da força foi invertido, pois q é negativa.
No cálculo do módulo do campo magnético você deve saber que Fe = 10-3 N (calculado em b) e que Fm = Fe = 10-3 N (devem se anular).
São dados: Fm = 10-3 N; q = 10-9 C; V = 100 = 102 m/s;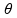 
= 90o (sen90o = 1) e B = ?
Fm = q.V.B.sen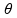 10-3 = 10-9. 102.B.1 B = 
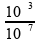B = 104 T
O campo magnético deve ser vertical, entrando na figura e ter intensidade (módulo)
B = 104T.
05-
Expressão matemática da lei da Gravitação Universal
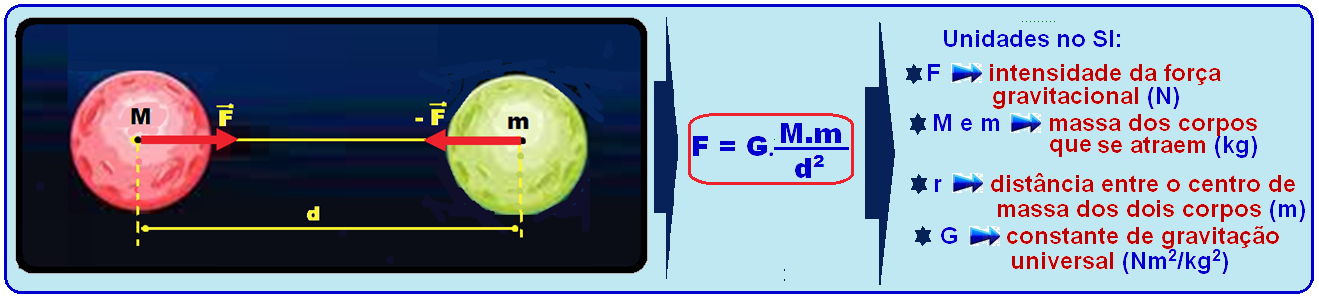
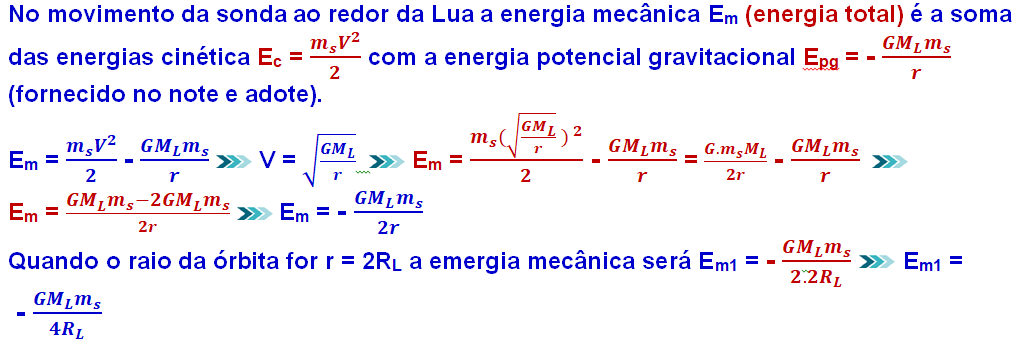
b)
Satélites em Órbitas Circulares
Satélite 
Qualquer objeto que gira em torno de um planeta em órbita circular ou elíptica.
06-
a)
As 4 forças que agem sobre a tábua são 4 e estão na figura abaixo:
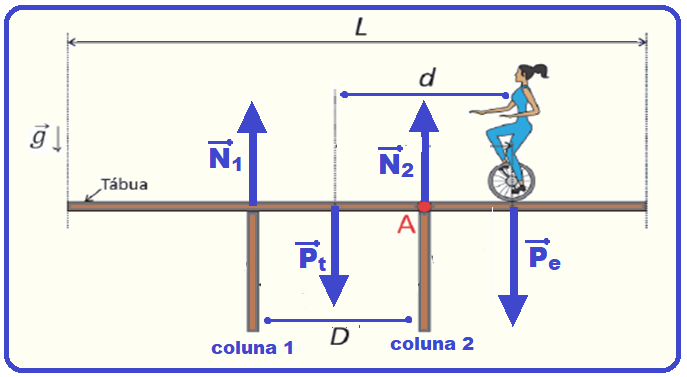
b) É pedido o torque (momento) resultante devido apenas aos pesos do peso da tábua 
e do equilibrista 
.
Cálculo do momento (torque) dessas forças com o polo em A e estabelecendo o sentido horário de rotação em torno do polo A como positivo.
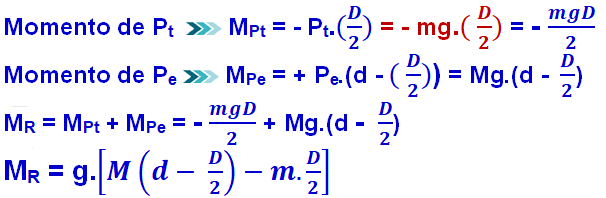
c) Considere os seguintes dados: comprimento da tábua: L = 5 m; massa da tábua: m = 20 kg, massa da equilibrista: M = 60 kg, distância entre as colunas: D = 3 m.
