CFS – Curso de Formação de Sargentos
EEAR 2019/20
Curso de Formação de Sargentos (CFS)
Escola de Especialistas de Aeronáutica (EEAR) é o maior complexo de ensino técnico militar da América do Sul sendo uma organização do Comando da Aeronáutica, diretamente subordinada ao diretor-geral do Departamento de Ensino da Aeronáutica (DEPENS), que tem por finalidade a formação e o aperfeiçoamento de graduados da Aeronáutica.
Está localizada no município de Guaratinguetá, entre as escarpas da Serra da Mantiqueira e das bordas da Serra da Quebra-Cangalha e Serra do Mar.
O Curso de Formação de Sargentos (CFS) tem a duração de dois anos e exige que os candidatos tenham concluído o ensino médio. Já o Estágio de Adaptação à Graduação de Sargento (EAGS) tem duração de aproximadamente um ano, e o candidato deve ter concluído o curso técnico relativo à especialidade de interesse da Força Aérea. Para realizar inscrição para ambos é necessário ser brasileiro(a), ter concluído o ensino médio, não ter menos de dezessete anos ou mais de vinte e quatro anos até a data da matrícula.
01- (Escola de Especialistas de Aeronáutica – EEAR – 019/020)
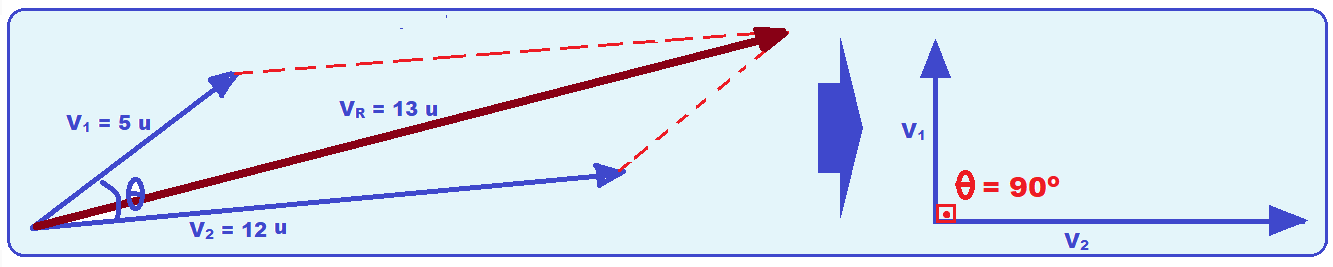
Dois vetores V1 e V2 formam entre si um ângulo e possuem módulos iguais a 5 unidades e 12 unidades, respectivamente.
Se a resultante entre eles tem módulo igual a 13 unidades, podemos afirmar corretamente que o ângulo entre os vetores V1 e V2 vale:
a) 0º b) 45º c) 90º d) 180º
02- (Escola de Especialistas de Aeronáutica – EEAR – 019/020)
Uma mola está suspensa verticalmente próxima à superfície terrestre, onde a aceleração da gravidade pode ser adotada como 10m/s2.
Na extremidade livre da mola é colocada uma cestinha de massa desprezível, que será preenchida com bolinhas de gude, de 15g cada.
Ao acrescentar bolinhas à cesta, verifica-se que a mola sofre uma elongação proporcional ao peso aplicado. Sabendo-se que a mola tem uma constante elástica k = 9,0N/m, quantas bolinhas é preciso acrescentar à cesta para que a mola estique exatamente 5 cm?
a) 1 b) 3 c) 5 d) 10
03- (Escola de Especialistas de Aeronáutica – EEAR – 019/020)
Um atleta pratica salto ornamental, fazendo uso de uma plataforma situada a 5m do nível da água da piscina.
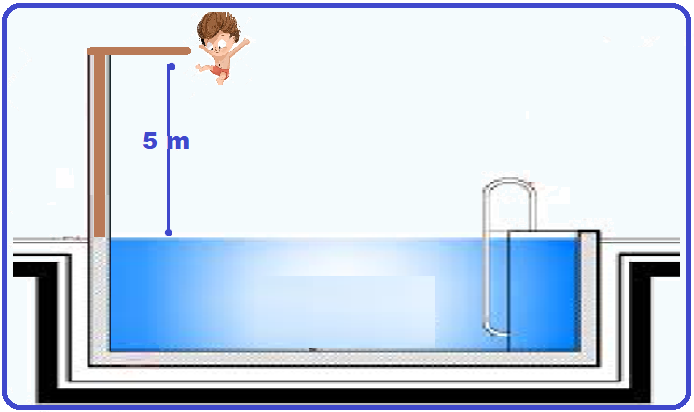
Se o atleta saltar desta plataforma, a partir do repouso, com que velocidade se chocará com a água? Obs.: despreze a resistência do ar e considere o módulo da aceleração da gravidade g = 10m/s2.
a) 10 m/s. b) 20 m/s. c) 30 m/s. d) 50 m/s.
04- (Escola de Especialistas de Aeronáutica – EEAR – 019/020)
Uma partícula com carga elétrica igual a 3,2 C e velocidade de 2.104 m/s é lançada perpendicularmente a um campo magnético uniforme e sofre a ação de uma força magnética de intensidade igual a 1,6 .102 N.
Determine a intensidade do campo magnético (em Tesla) no qual a partícula foi lançada.
a) 0,25.103 b) 2,5.103 c) 2,5.104 d) 0,25.106
05- (Escola de Especialistas de Aeronáutica – EEAR – 019/020)
Um adolescente de 12 anos, percebendo alterações em sua voz, comunicou à sua mãe a situação observada com certa regularidade. Em determinados momentos apresentava tom de voz fina em outros momentos tom de voz grossa.
A questão relatada pelo adolescente refere-se a uma qualidade do som denominada:
a) altura. b) timbre. c) velocidade. d) intensidade.
06- (Escola de Especialistas de Aeronáutica – EEAR – 019/020)
Considere quatro esferas metálicas idênticas, A, B, C e D, inicialmente separadas entre si.
Duas delas, B e D, estão inicialmente neutras, enquanto as esferas A e C possuem cargas elétricas iniciais, respectivamente, iguais a 3Q e -Q.
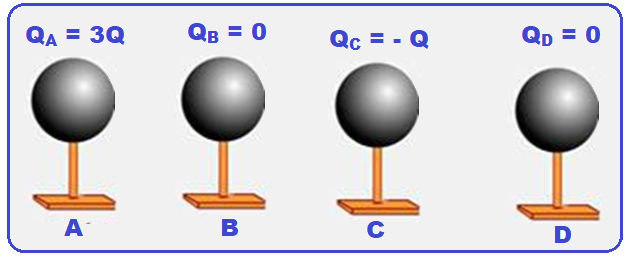
Determine a carga elétrica final da esfera C após contatos sucessivos com as esferas A, B e D, nessa ordem, considerando que após cada contato, as esferas são novamente separadas.
a) Q/4 b) Q/2 c) 2Q d) 4Q
07- (Escola de Especialistas de Aeronáutica – EEAR – 019/020)
Um astronauta de massa m e peso P foi levado da superfície da Terra para a superfície de um planeta cuja aceleração da gravidade, em módulo, é igual a um terço da aceleração da gravidade registrada na superfície terrestre.
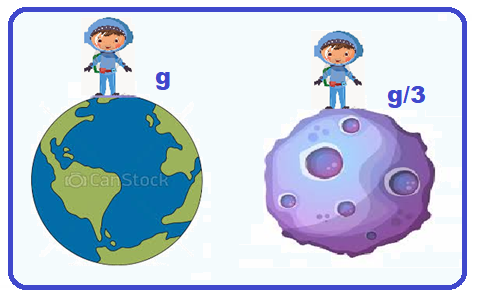
No novo planeta, os valores da massa e do peso desse astronauta, em função de suas intensidades na Terra, serão respectivamente:
a) m/3 , P b) m, P c) m, P/3 d) m/3 , P/3
08- (Escola de Especialistas de Aeronáutica – EEAR – 019/020)
Roberto, empolgado com as aulas de Física, decide construir um termômetro que trabalhe com uma escala escolhida por ele, a qual chamou de escala R. Para tanto, definiu – 20°R como ponto de fusão do gelo e 80°R como temperatura de ebulição da água, sendo estes os pontos fixos desta escala. Sendo R a temperatura na escala criada por Roberto e C a temperatura na escala Celsius, e considerando que o experimento seja realizado ao nível do mar, a expressão que relaciona corretamente as duas escalas será:
a) C = R – 20
b) C = R + 20
c) C = (R 20)/2
d) C = (R 20)/2
09- (Escola de Especialistas de Aeronáutica – EEAR – 019/020)
O gráfico a seguir corresponde ao comportamento da corrente elétrica que percorre um condutor, em função da diferença de potencial a ele aplicada.
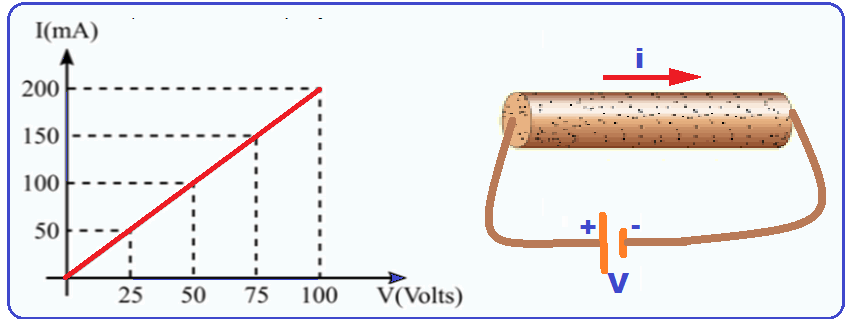
Sabendo-se que este condutor é constituído de um fio de 2m de comprimento e de um material cuja resistividade, a 20°C, vale 1,75. 10-6 .m, determine a área da seção transversal do fio e o valor da resistência elétrica desse condutor na referida temperatura.
a) 0,7.10-4 cm2 e 0,5
b) 0,7.10-4 cm2 e 500
c) 0,83.10-4 cm2 e 12,5
d) 0,83.10-4 cm2 e 500
Resolução comentada das questões de Física da Escola de Especialistas de Aeronáutica – EEAR – 019/020
01-
Soma de dois vetores pelo Método do paralelogramo
Coloque a origem dos dois vetores em um mesmo ponto e, em seguida, trace pelas extremidades de cada um deles, uma paralela ao outro, com linha pontilhada.
Unindo os pontos indicados e colocando a seta conforme a figura acima, você obterá o vetor
que é o vetor soma ou o vetor resultante.
Sendo β o ângulo entre os dois vetores, pode-se determinar o módulo ou intensidade do vetor pela lei dos cossenos:
No caso do exercício V1 = 5 u, V2 = 12 u, a o vetor resultante tem VR = 13 u e o ângulo entre eles é θ.
Aplicando a lei dos cossenos 
VR2 = V12 + V22 + 2.V1.V2.cosθ 132 = 52 + 122 + 2.5.12.cosθ
169 = 25 + 144 + 120.cosθ 169 – 169 = 120.cosθ cosθ = 0/120 cosθ = 0 se cosθ = 0
θ = 90o e V1 e V2 são perpendiculares entre si.
R- C
02-
Força elástica – Lei de Hooke
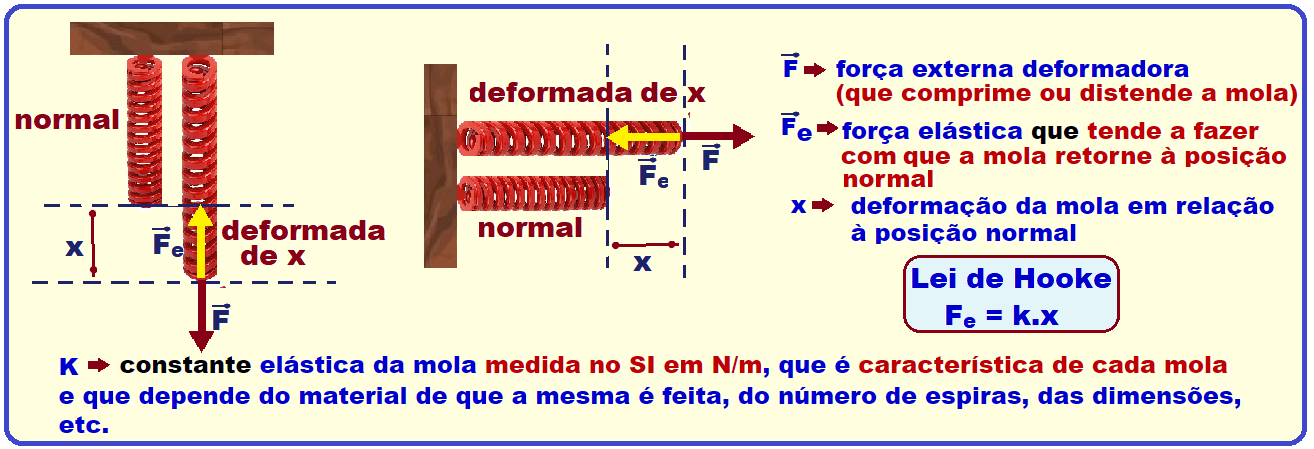
Cálculo do módulo da força elástica (vertical e para cima) quando (com as bolinhas) a mola está deformada de x = 5 cm = 0,05 m e com K = 9 N/m
Fe = K.x = 9.0,05 Fe = 0,45 N.
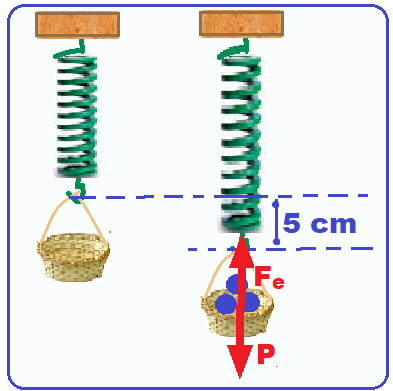
Com a cesta em equilíbrio o peso P das n bolinhas (vertical e para baixo) é equilibrado pela força elástica, ou seja P =n.m.g = n.0,015.10 P = n.0,15 = Fe 0,15n = 0,45 n = 0,45/0,15 n = 3 bolinhas.
R- B
03-
Queda livre vertical
Corpo abandonado de certa altura h do solo
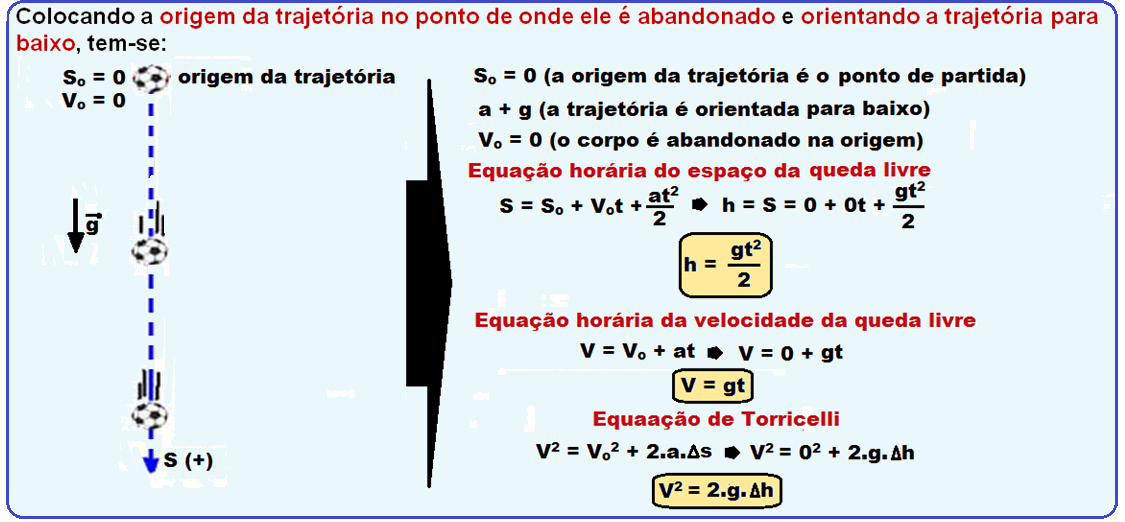
Aplicando a equação de Torricelli V2 = 2.g.h = 2.10.5 =100 V = 10 m/s.
R- A
04-
Carga elétrica q lançada com velocidade 
lançada perpendicularmente às linhas de indução de um campo magnético uniforme
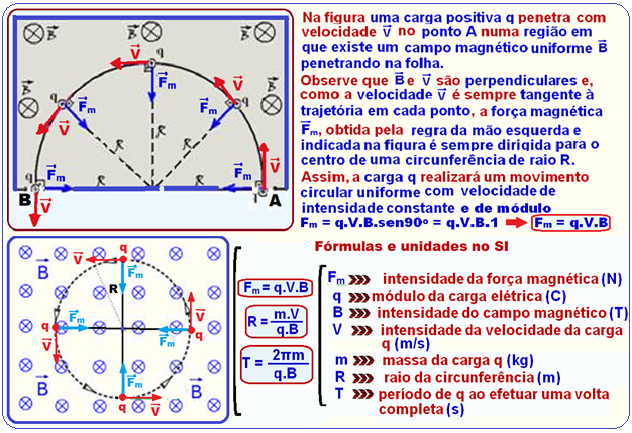
São dados: q = 3,2µC = 3,2.10-6 C; V = 2.104 m/s; F = 1,6.102 N e B = ?
Fm = q.V.B 1,6.102 = 3,2.10-6.2.104.B 1,6.102 = 6,4.10-2.B B = 1,6.102/6,4.10-2 B = 0,25.104 = 2,5.103 T.
R – B
05-
Altura do som
A velocidade de vibração da fonte sonora (lâmina, corda, membrana, etc.) é que vai definir sua altura.
As vibrações lentas produzem sons graves (baixos e grossos) e as vibrações rápidas produzem sons agudos (altos e finos).
A altura dos sons depende também do tamanho dos corpos que vibram. Uma corda fina e curta produz sons mais agudos que os de uma corda longa e grossa.
Uma flauta pequenina de tubo bem fino também produz sons mais agudos do que um instrumento de sopro com um tubo longo e grosso como a tuba.
A altura do som está relacionada com sua frequência, ou seja, a altura (tom) é a qualidade do som que permite ao ouvido distinguir um som grave, de baixa frequência, de um som agudo, de alta frequência.
R- A
06-
Eletrização por contato
Pode ocorrer entre dois condutores (cargas elétricas se distribuem em suas superfície externas) ou entre um condutor e um isolante (no isolante as cargas elétricas ficam somente no local do contato).
Considere um condutor A eletrizado com carga positiva (QA = + Q) e outro condutor B, eletricamente
neutro (QB = 0) presos a suportes isolantes (para que não descarreguem, inicialmente separados.
Quando são colocados em contato, os dois se comportam como se fossem um único corpo e haverá uma distribuição de cargas nas superfícies de A e de B.
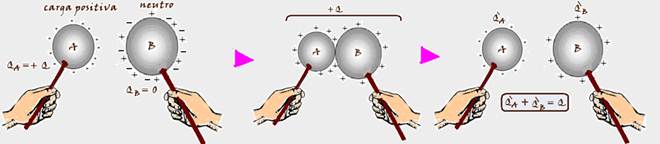
Após essa distribuição de cargas são separados e A ficará com carga QA’ e B com carga QB’, tal que QA’ + QB’ = + Q (princípio da conservação das cargas elétricas).
Observe que, se os condutores forem idênticos e com as mesmas dimensões, você teria QA’ = QB’= Q’ 
Q’ + Q’ = + Q Q’=Q/2
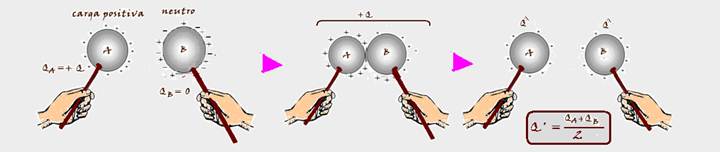
Se os dois corpos forem idênticos e estiverem inicialmente eletrizados com cargas QA e QB, após o contato eles terão cargas idênticas Q’ tal que Q’= (QA + QB)/2.
No caso do exercício:
R- A
07-
A massa uma grandeza escalar, positiva e invariável para cada corpo não dependendo do lugar onde ele se encontra.
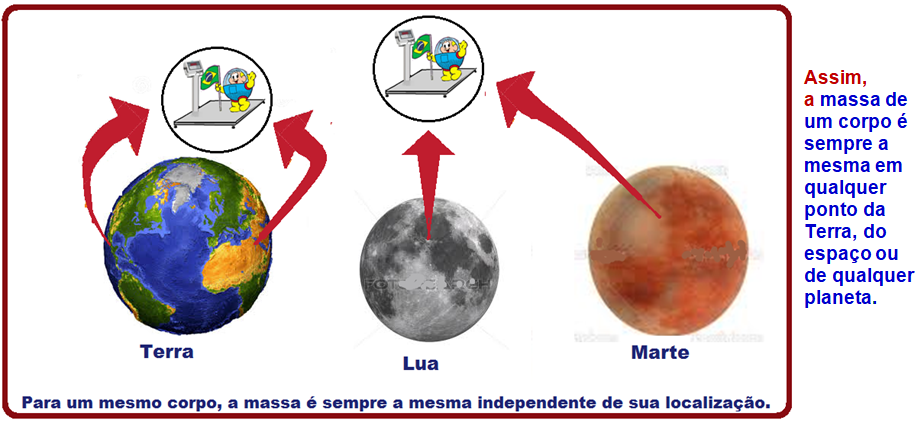
Peso
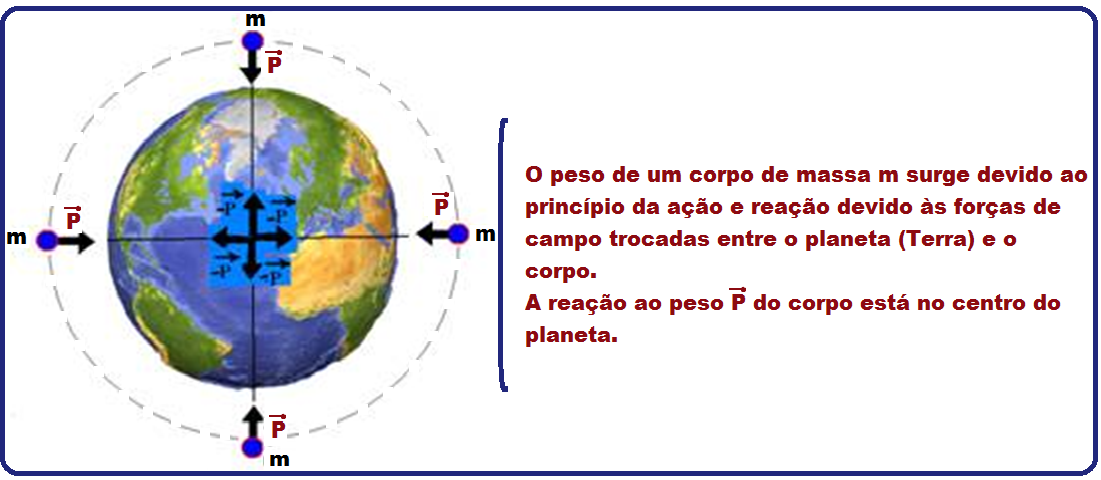
A massa é a mesma (Veja teoria acima).
Na expressão P = m.g, como m é constante, o peso P é diretamente proporcional à aceleração da gravidade g. Assim, se g do planeta é 3 vezes menor a que a da Terra, o peso P do astronauta no planeta também será 3 vezes menor.
R- C
08-
Relacionando as escala Celsius e R:
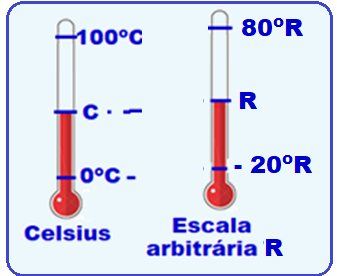
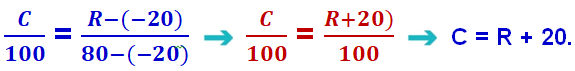
R- B
09-
Primeira lei de Ohm
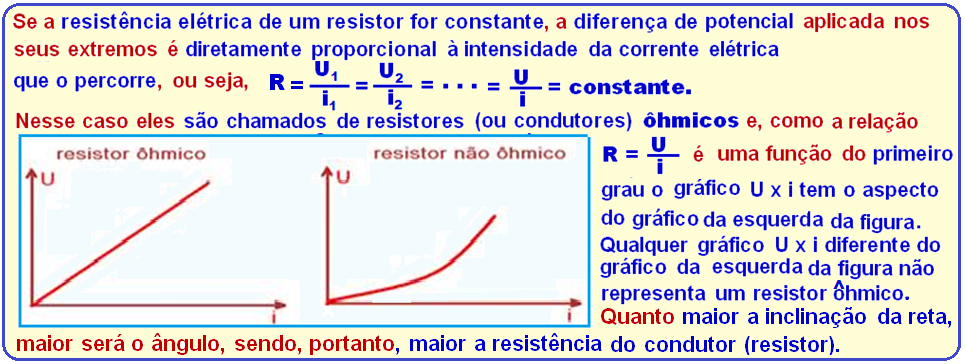
Segunda lei de Ohm (Resistividade)
O gráfico Vxi fornecido refere-se à primeira lei de Ohm (teoria acima) onde R é constante para quaisquer valores de V e i e, por exemplo, escolhendo quando V = 50 V, i = 100 mA = 100.10-3 A = 0,1 A R = v/i R = 50/0,1 R = 500 Ω.
Aplicando agora a 2a lei de Ohm (veja teoria acima) sendo dados: R = 500 Ω; L = 2 m e 
1,75. 10-6 .m R = 
/S 500 = 1,75.10-6.2/S 500S = 3,5.10-6 S = 3,5.10-6/5.102 = 0,7.10-8 m2 = 0,7.
10-8.104 S = 0,7.10-4 cm2.
R- B