UNITAU 2019
UNITAU – MEDICINA – 2019
Faculdade de Medicina de Taubaté (FMT), ligada hoje à Universidade de Taubaté, é uma escola de medicinado Interior de São Paulo, localizada no Campus do Bom Conselho, em Taubaté. É a única escola de medicina do Vale do Paraíba e uma das mais antigas do interior do Estado de São Paulo.
Por pertencer a uma universidade de caráter municipal e filantrópica, a faculdade possui diversos programas de bolsas de estudos que variam de 20% até 100% de desconto nas mensalidades. A Unitau disponibiliza cerca de 1,8 milhões de reais por ano para bolsas Simube (além de outros programas de bolsas e descontos oferecidos pela universidade). Por essa mesma razão, a FMT possui uma das menores mensalidades dentre as faculdades de medicina do estado de São Paulo.
A Faculdade ainda disponibiliza bolsas de iniciação científica e monitoria da própria universidade (PIC, PIBIC), do CNPq (governo federal) e FAPESP(governo de São Paulo).
01- (Faculdade de Medicina de Taubaté – FMT – 019)
A figura abaixo mostra um objeto, de massa M, em equilíbrio estático, suspenso por cabos cujas extremidades estão presas ao teto de uma sala.
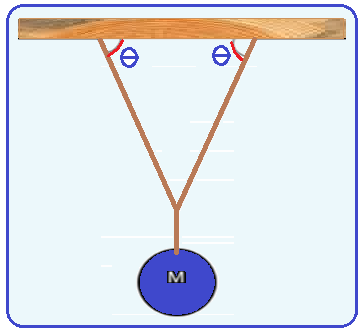
Considere o módulo da aceleração gravitacional terrestre g = 10m/s2 . Sabendo que o ângulo θ é de 300 , e que a tensão máxima suportada por cada um dos cabos utilizados é de 2 kN, qual é o valor máximo de M suportado pelo sistema? Dados: sen(300) = 0,5 e cos(300) = 0,87
a) 0,2 kg b) 10 kg c) 100 kg d) 200 kg e) 2000 kg
02- (Faculdade de Medicina de Taubaté – FMT – 019)
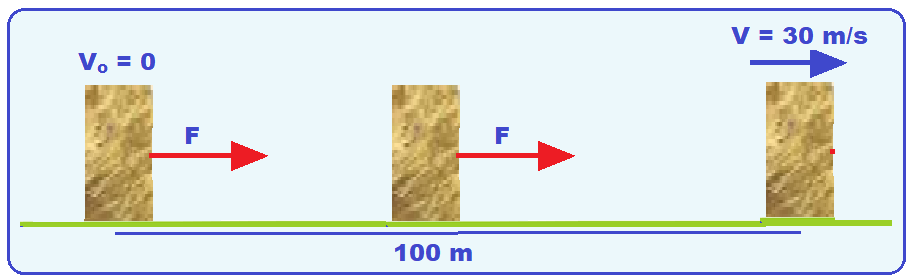
Considere um objeto inicialmente em repouso e apoiado sobre uma superfície horizontal e plana. Esse objeto foi arrastado de modo a descrever um movimento de translação, com trajetória linear de 100 m, e sempre apoiado sobre a superfície, até atingir a velocidade de 30 m/s.
Desconsidere todos os tipos de atrito que poderiam atuar sobre o sistema. Sabendo que a massa do objeto é de 90 kg, calcule o módulo da força resultante que atuou sobre o objeto ao longo da trajetória até atingir a velocidade de 30 m/s.
a) 102 N b) 205 N c) 405 N d) 810 N e) 1215 N
03- (Faculdade de Medicina de Taubaté – FMT – 019)
Uma partícula, que é um objeto cujas dimensões são desprezíveis em relação às demais dimensões envolvidas no problema, deve percorrer uma distância linear (movimento em linha reta) de 320 m.
A distância será percorrida com um movimento retilíneo, uniformemente acelerado, sendo nula a velocidade inicial. Desconsidere todos os tipos de atrito que poderiam atuar sobre o sistema. Calcule o módulo da aceleração do movimento para que a velocidade média ao longo dos 320 m seja de 8 m/s.
a) 0,2 m/s2 b) 0,4 m/s2 c) 0,5 m/s2 d) 2,0 m/s2 e) 4,0 m/s2
04- (Faculdade de Medicina de Taubaté – FMT – 019)
Um pêndulo simples é composto por um objeto, cujas dimensões são desprezíveis, preso a uma linha inextensível, sendo o comprimento da linha muito maior do que as dimensões do objeto. A outra extremidade da linha é fixada em um suporte, ou mesmo ao teto, como mostra a figura.
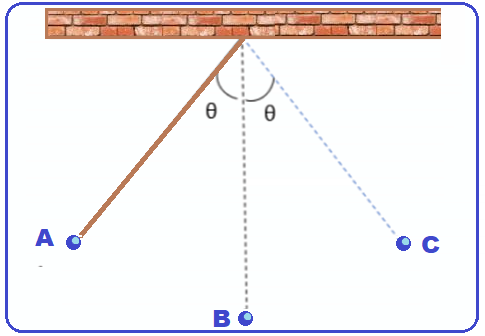
A posição de equilíbrio estático do pêndulo corresponde ao ponto B. Entretanto, ao ser deslocado até o ponto A e, posteriormente, ao ser abandonado, a partir do repouso, o pêndulo passa a desenvolver um movimento periódico do ponto A até o ponto C, passando por B, e, depois, fazendo o movimento inverso.
No sistema representado na figura, a massa do objeto pendurado na extremidade da linha é de 10 g; o comprimento da linha inextensível é de 2,0 m; o módulo da aceleração gravitacional terrestre pode ser adotado como 10 m/s2; a massa do fio inextensível é desprezível, e todos os tipos de atrito podem ser desprezados para o movimento desse pêndulo. Sabendo que a energia cinética da massa m, ao passar pelo ponto B, é de 0,1 J, o cosseno do ângulo de abertura inicial do pêndulo (cos θ) é igual a
a) 0,98 b) 0,87 c) 0,65 d) 0,71 e) 0,50
05- (Faculdade de Medicina de Taubaté – FMT – 019)
Considere um objeto cujas dimensões são desprezíveis. No instante de tempo t = 0 s, esse objeto é abandonado, a partir do repouso, de uma altura de H = 80 m, medida em relação ao solo. No mesmo instante em que o objeto é abandonado (t=0 s), uma pessoa, situada a uma distância linear R = 40 m do ponto em que o objeto irá tocar o solo, começa a se deslocar em movimento retilíneo uniforme em direção ao ponto de colisão.
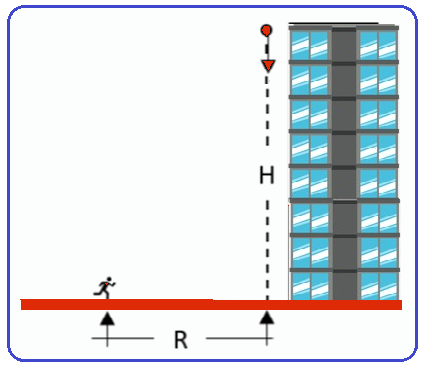
Sobre o movimento descrito, é totalmente CORRETO afirmar:
a) Se a velocidade média de deslocamento da pessoa for igual a 5 m/s, ela estará a uma distância de 20 m do ponto de colisão quando o objeto atingir o solo.
b) Se a velocidade média de deslocamento da pessoa for igual a 8,0 m/s, ela percorrerá a distância R no mesmo intervalo de tempo que o objeto levará para atingir o solo.
c) Se a velocidade média de deslocamento da pessoa for igual a 9,5 m/s, ela estará a 8 m de distância do ponto de colisão quando o objeto atingir o solo.
d) Se a velocidade média de deslocamento da pessoa for igual a 12,0 m/s, ela passará pelo ponto de colisão dois segundos antes de o objeto atingir o solo.
e) Se a velocidade média de deslocamento da pessoa for igual a 8,0 m/s, ela chegará ao ponto de colisão dois segundos após o objeto atingir o solo.
06- (Faculdade de Medicina de Taubaté – FMT – 019)
Uma partícula com carga positiva é injetada com velocidade V numa região com campos elétrico e magnético cruzados e passa a se movimentar em uma trajetória retilínea.
O campo magnético é um vetor que sai perpendicularmente à folha do papel, enquanto o campo elétrico é paralelo à folha, conforme apresentado na figura abaixo.
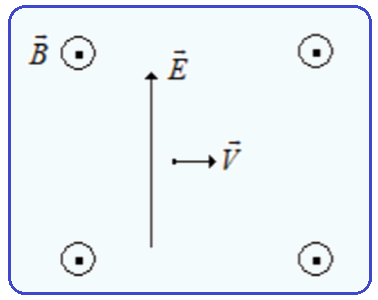
Sabendo que E e B são os módulos dos campos elétrico e magnético, determine o módulo da velocidade V nessa região e assinale a alternativa CORRETA.
a) V = E/B
b) V = B/E
c) V = EB
d) V = E/B2
e) V = B/E2
07- (Faculdade de Medicina de Taubaté – FMT – 019)
Considere o circuito representado abaixo. Após fecharmos a chave faca F, o gerador não ideal alimenta o resistor R1 de 100 ohms.
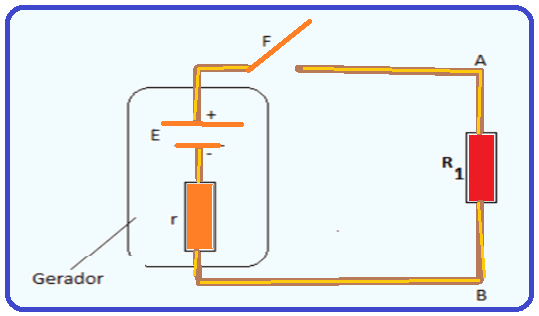
Sabendo que a resistência interna do gerador é de r = 20 ohms, e que a força eletromotriz do gerador é de 120 volts, a potência dissipada no gerador, medida em watts, é de
a) 100 b) 50 c) 40 d) 30 e) 20
08- (Faculdade de Medicina de Taubaté – FMT – 019)
Um agitador é usado para aquecer uma certa quantidade de água, contida num recipiente termicamente isolado.
Considere que o calor específico da água é 1 cal/(g.oC).
Admitindo que 1 cal = 4,2 J, determine a variação de temperatura sofrida por uma massa de água de 400 g que recebe desse agitador 4,2.104 J de energia.
a) 25,0 graus Celsius
b) 52,0 graus Celsius
c) 22,0 graus Celsius
d) 55,0 graus Celsius
e) 2,50 graus Celsius
09- (Faculdade de Medicina de Taubaté – FMT – 019)
Qual quantidade de energia um agitador deve fornecer a 200 g de água, que está inicialmente no estado líquido e a zero graus Celsius, para levar essa água até a temperatura de vapor (100 ºC)?
Sabe-se que o calor específico da água é 1cal/(g.oC) e que 1 cal = 4,2 J.
a) 4,40.104 J
b) 8,40.104 J
c) 44,0.104 J
d) 48,0.104 J
e) 84,0.104 J
Resolução comentada das questões de Física da Faculdade de Medicina de Taubaté – FMT – 019
01-
Colocando as forças que agem sobre cada fio (figura 1) e decompondo-as (figura 2).
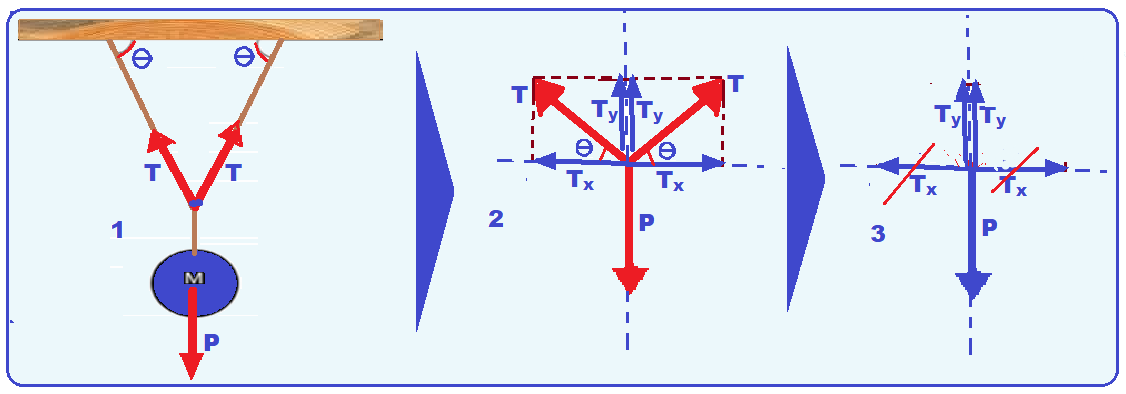
Observe na figura 3 que as projeções de T na horizontal de anulam (equilíbrio horizontal).
Projeção de T na vertical 
Ty = T.sen30o = 2k.0,5 Ty = 1 kN.
Equilíbrio na vertical 2Ty = P 2.1k = P P = 2 kN = 2000 N.
P = m.g 2000 = m.10 m = 2000/10 m = 200 kg.
R- D
02-
Cálculo da aceleração a do corpo de massa m = 90 kg pela equação de Torricelli após o deslocamento de d = 100 m V2 = Vo2 + 2.a.d 302 = 02 + 2.a.100 900 = 200.a a = 900/200 a = 4,5 m/s2.
Como o movimento é na horizontal as forças verticais normal e peso se anulam e não existindo atrito a força resultante é F tal que, pela segunda lei de Newton F = m.a = 90.4,5 = 405 N.
R – C
03-
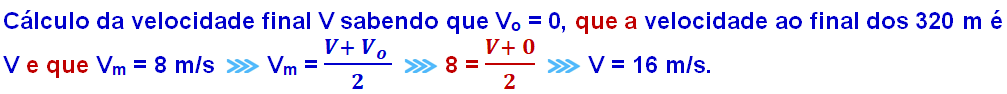
R- B
04-
Como os atritos são desprezados o sistema é conservativo e a energia mecânica em B que é a cinética EmB = EcB = 0,1 J (EpB = 0, pois em B h = 0) é a mesma que em A que é a potencial gravitacional EMA = EpA = 0,1 j (EcA = 0, pois a velocidade em A é nula).
EmB = m.g.h 0,1 = 0,01.10.h h = 0,1/0,1 h = 1m (veja figura abaixo)
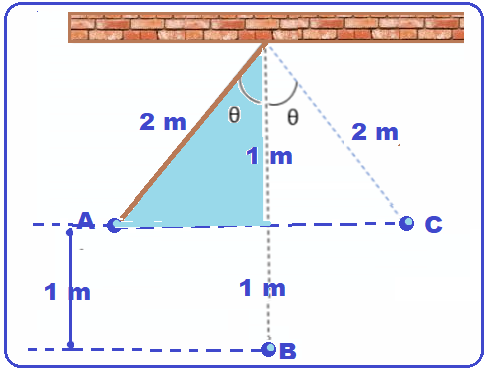
No triângulo hachurado cosθ = cateto adjacente/hipotenusa = 1/2 cosθ = 0,50.
R- E
05-
Corpo abandonado de certa altura h do solo
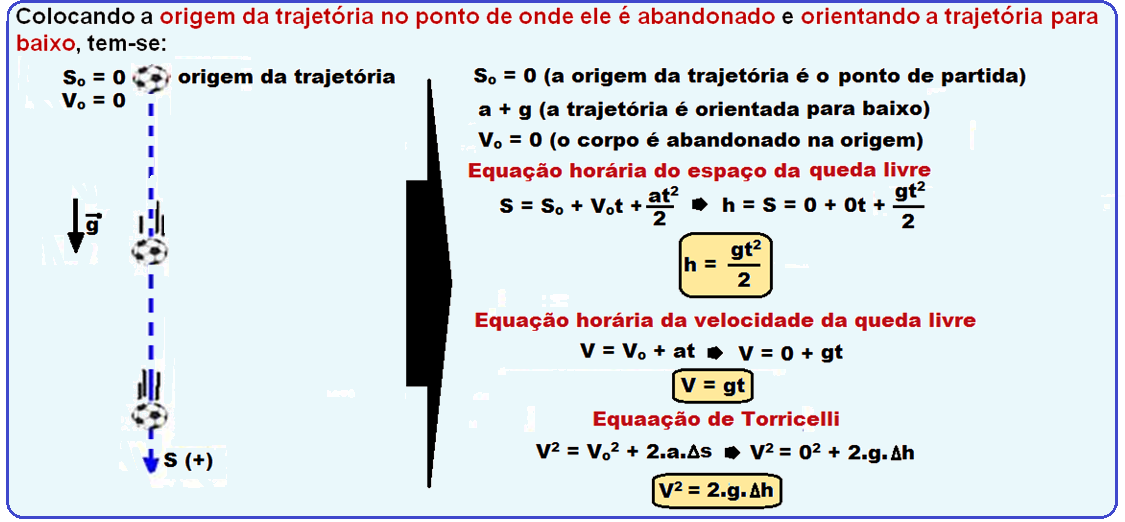
Cálculo do tempo que demora para chegar ao solo em queda livre percorrendo h = 80 m h = g.t2/2 80 =10t2/2 t2 = 16 t = 4 s.
Cálculo da velocidade média da pessoa para chegar exatamente no ponto de colisão do objeto com o solo que demora t = 4 s percorrendo os d = 40 m Vm = d/t Vm = 40/4 Vm = 10 m/s.
Analisando cada afirmativa você comprova que a (A) é a correta, pois se V = 5 m/s em t = 4s a pessoa percorrerá Vm = d/t 5 = d/4 d = 20 m e estará a 20 m do ponto de colisão quando o objeto atingir o solo que ocorre quando ela percorre 40 m.
R- A
06-
Veja abaixo um resumo da teoria:
Características do Vetor Campo Elétrico
Carga elétrica q lançada com velocidade 
lançada perpendicularmente às linhas de indução de um campo magnético uniforme
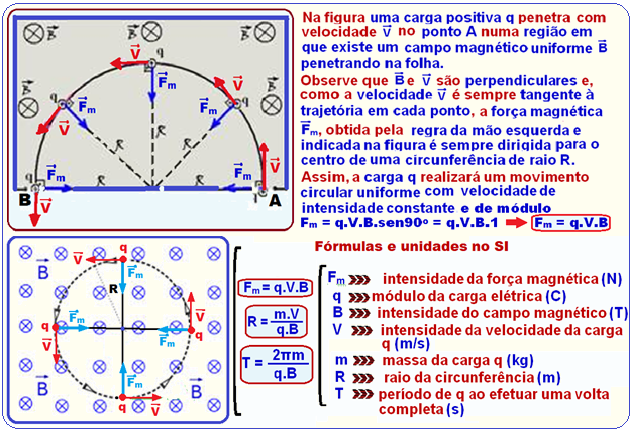
Força sobre q devido ao campo elétrico E = F/q F = q.E (I)
Força sobre q devido ao campo magnético F = q.V.B (II)
(I) = (II) q.E = q.V.B V = E/B.
R- A
07-
Cálculo da resistência do resistor equivalente onde R = 100 Ω e r = 20 Ω estão em série Req = R + r = 100 + 20 Req = 120 Ω
Cálculo da corrente elétrica i no circuito Req = (U = E)/i 120 = 120/i i 120/120 i = 1 A.
A potência dissipada no gerador é devida a sua resistência interna r = 20 Ω e fornecida por P = r.i2 = 20.12 = 20.1 P = 20 W
R- E
08-
W = Q = 4,2.104 j/4,2 = 104 cal.
Q = m.c ∆t 104 = 400.1.∆t ∆t = 10000/400 ∆t = 25 o C.
R- A
09-
Q = m.c.∆t = 200.1.100 W = 2.104 calx4,2 = 8,4.104 J.
R- B