Termomecânica 2019 – 2o Semestre

Termomecânica – 2019 – 2^o semestre

Faculdade de Tecnologia Termomecanica

Na Faculdade de Tecnologia Termomecanica, o aluno recebe gratuitamente um curso que corresponde a um investimento financeiro anual por aluno de quase R$ 25 mil. Além do modelo de educação inovador e gratuito, que inclui formação humanista, todos os universitários recebem gratuitamente uniformes e alimentação balanceada. A FTT ainda possui parceria com mais de 130 empresas nacionais e multinacionais e 11 agentes de integração de estágio. Em 12 anos, a instituição já preparou quase 1,3 mil profissionais para o mercado de trabalho e conquistou índice de 86,7% de empregabilidade.

A grade curricular dos quatro cursos superiores oferecidos pela Faculdade de Tecnologia Termomecanica – Administração, Engenharia de Alimentos, Engenharia de Computação e Engenharia de Controle e Automação – possui também aulas de empreendedorismo, libras, recuperação e nivelamento. Além disso, cursos de extensão são oferecidos gratuitamente aos alunos.

A Faculdade de Tecnologia Termomecânica está localizada no Centro Educacional da Fundação Salvador Arena, no município de São Bernardo do Campo, na Grande São Paulo. O complexo educacional de 131 mil m² recebeu investimentos de mais de R$ 350 milhões em educação nos últimos 15 anos e, além de laboratórios com equipamentos de última geração, possui ginásios e quadras poliesportivos, conjunto aquático, estádio olímpico, uma rede de bibliotecas interativas e um dos teatros mais modernos do Brasil, com capacidade para 600 pessoas.

Em nota divulgada em 17 de novembro de 2016, pelo Ministério da Educação, a Faculdade de Tecnologia Termomecânica obteve nota quatro no IGC – Índice Geral de Cursos. O IGC é uma das medidas usadas pelo Inep para avaliar as instituições de educação superior, públicas e privadas, classificando-as com notas de um a cinco.

De acordo com esse levantamento, a Faculdade de Tecnologia Termomecanica ocupa o 1º lugar entre as instituições de ensino superior das três principais cidades do ABC, a 7ª no Estado de São Paulo e a 33ª, entre todas as faculdades do Brasil. A colocação é um orgulho para uma faculdade que iniciou suas atividades há menos de uma década e que se equipara a instituições já consagradas de nosso País.

01 – (Faculdade de Tecnologia Termomecânica – SP- 019)

Observe a figura, onde se destaca uma placa de fiscalização eletrônica de velocidade.

No Sistema Internacional de Unidades, os valores indicados na placa estão compreendidos no intervalo de

(A) 15 m/s a 25 m/s.

(B) 18 m/s a 22 m/s.

(C) 10 m/s a 20 m/s.

(D) 18 m/s a 32 m/s.

(E) 20 m/s a 50 m/s.

 

02 – (Faculdade de Tecnologia Termomecânica – SP- 019)

O gráfico representa a variação da velocidade escalar de um móvel em função do tempo, sendo t₁ o instante em que a reta intercepta o eixo do tempo.

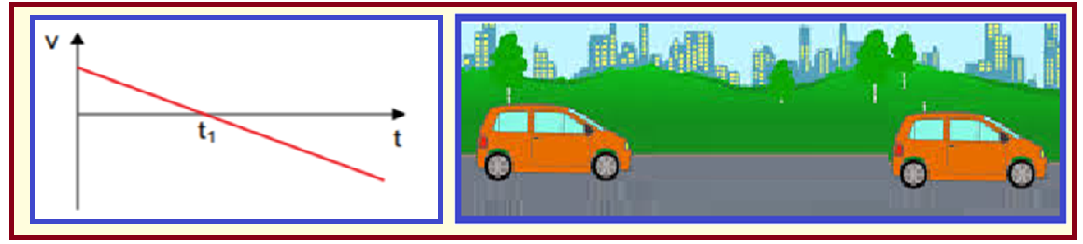
A alternativa que representa corretamente o gráfico da aceleração escalar desse móvel, também em função do tempo, é:

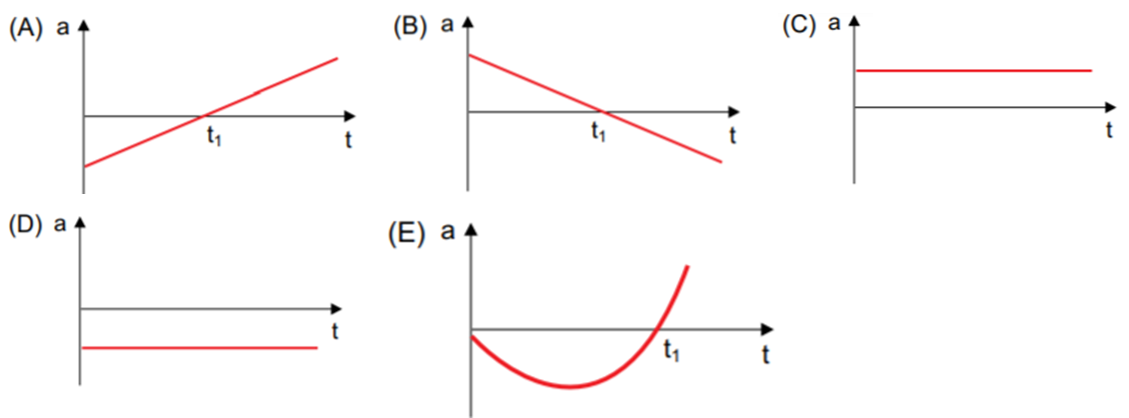
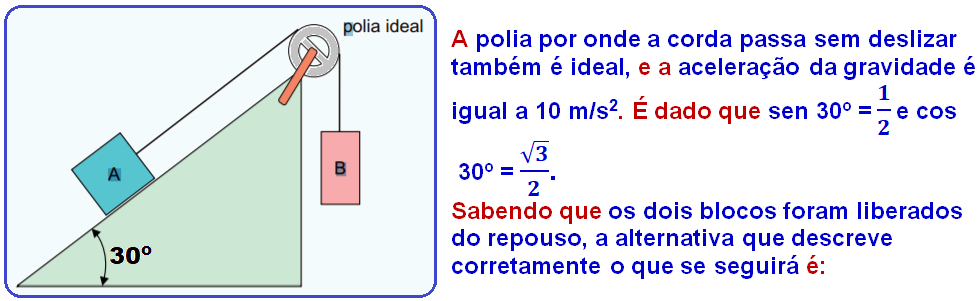
03 – (Faculdade de Tecnologia Termomecânica – SP- 019)

A ilustração mostra dois blocos, A, de 40 kg, e B, de 20 kg, estando A apoiado sobre um plano inclinado sem atrito, enquanto B está pendurado numa corda ideal que interliga os dois blocos.

(A) os dois blocos se manterão em repouso.

(B) o bloco A subirá sobre o plano inclinado com aceleração 2 m/s² .

(C) o bloco A descerá sobre o plano inclinado com aceleração 2 m/s² .

(D) o bloco B descerá com velocidade constante igual a 2 m/s.

(E) o bloco B subirá com velocidade constante igual a 2 m/s

 

04 – (Faculdade de Tecnologia Termomecânica – SP- 019)

Considere o patinador da figura lançando-se horizontalmente sobre uma superfície de gelo sem atrito, inicialmente a 40 metros de altitude e com velocidade 20 m/s, como mostra a figura.

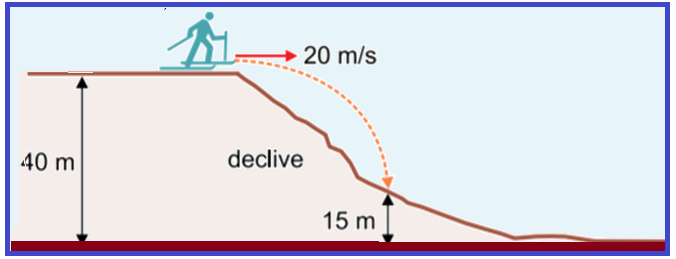
A aceleração da gravidade é igual a 10 m/s² e não há dissipação de energia mecânica em todo o movimento do patinador, considerado como um ponto material. Sabendo que ele atinge o declive a 15 metros de altitude, a alternativa que indica corretamente sua velocidade, nesse instante, é

(A) 25 m/s. (B) 30 m/s. (C) 35 m/s. (D) 40 m/s. (E) 45 m/s.

 

05 – (Faculdade de Tecnologia Termomecânica – SP- 019)

Com o propósito de medir a temperatura de um forno, um fragmento de ferro é inserido em seu interior, sendo aí deixado um tempo suficiente para que entre em equilíbrio térmico com o forno.

Num dado momento, o fragmento é retirado do forno e rapidamente jogado dentro de um calorímetro ideal, contendo água inicialmente a 20 ºC e com uma massa igual à do fragmento de ferro. O calor específico do ferro é 0,12 cal/(g.ºC) e da água é 1,0 cal/(g.ºC).

Após certo tempo, verifica-se que a temperatura de equilíbrio térmico entre o ferro e a água é igual a 80 ºC.

Sabendo que durante a passagem do forno para o calorímetro não houve variação de temperatura no fragmento de ferro e que a troca de calor ocorreu apenas entre o ferro e a água, a alternativa que indica corretamente a temperatura do forno é:

(A) 320 ºC. (B) 410 ºC. (C) 460 ºC. (D) 540 ºC. (E) 580 ºC

 

06 – (Faculdade de Tecnologia Termomecânica – SP- 019)

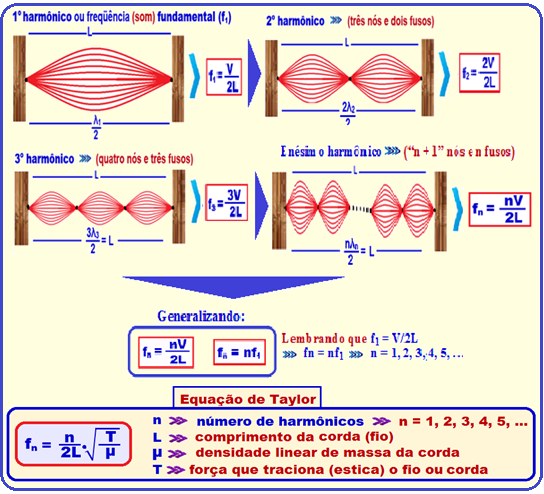
A figura mostra os primeiros quatro modos de vibração de uma corda em regime estacionário e com os dois extremos fixos, onde V é o ventre, e N, o nó da onda.

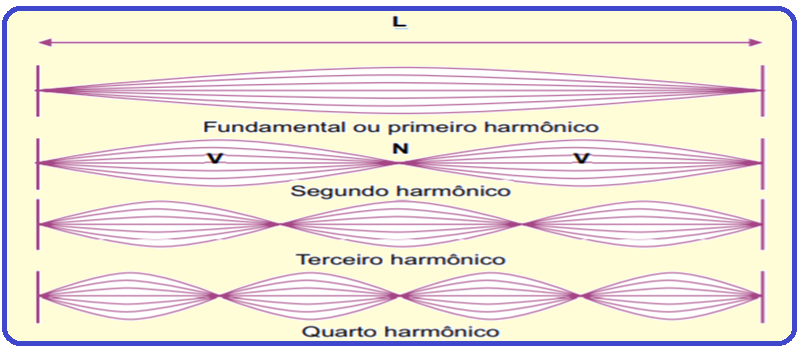
Sendo L a distância entre os dois extremos fixos no modo fundamental, o comprimento de onda no décimo harmônico será de

A) 0,1 L. (B) 0,2 L. (C) 0,3 L. (D) 0,4 L. (E) 0,5 L.

07 – (Faculdade de Tecnologia Termomecânica – SP- 019)

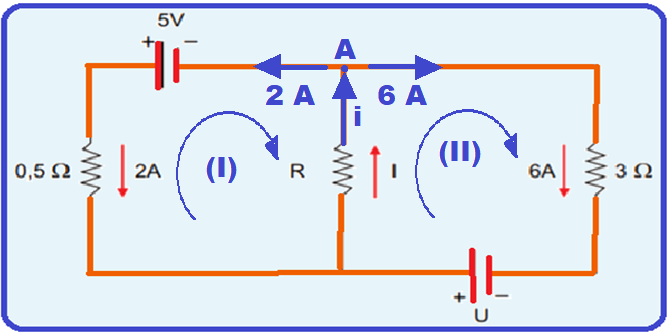
A figura mostra um circuito elétrico formado por duas malhas, havendo um gerador elétrico em cada uma.

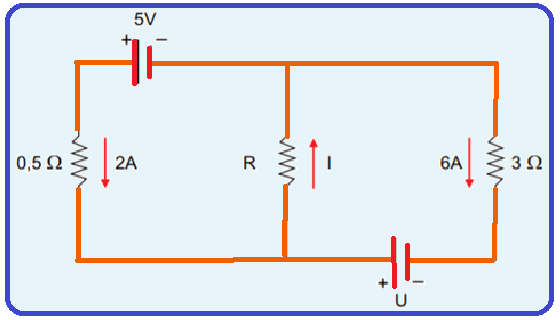
Sabendo que as setas indicam os sentidos reais das correntes elétricas nestes ramos, a alternativa que apresenta os valores corretos de I, R e U, respectivamente, é

(A) 5 A ; 1,0 Ω ; 12 V.

(B) 5 A ; 1,2 Ω ; 14 V.

(C) 8 A ; 1,0 Ω ; 10 V.

(D) 8 A ; 0,5 Ω ; 22 V.

(E) 10 A ; 5 Ω ; 9 V

 

08 – (Faculdade de Tecnologia Termomecânica – SP- 019)

Considere um corpo esférico, constituído de casca e caroço, ambos homogêneos e de mesmo volume, mas feitos com materiais diferentes, como mostra a figura.

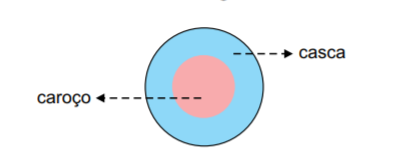
Verifica-se que, quando colocado na superfície da água, o corpo flutua com 60% de seu volume total submerso. Sendo a densidade absoluta da água igual a 1,0 kg/L, e a densidade absoluta do material que constitui a casca igual a 0,4 kg/L, a alternativa que indica corretamente a densidade absoluta do material que constitui o caroço é

(A) 0,4 kg/L. (B) 0,6 kg/L. (C) 0,8 kg/L. (D) 1,0 kg/L. (E) 1,2 kg/L.

Resolução comentada das questões de Física da Faculdade de Tecnologia Termomecânica – SP- 019

01-

 

Em m/s 60/3,6 = 16,66 m/s 80/3,6 = 22,22 m/s veja na alternativa A que 15 m/sx3,6 = 54 km/h e que 25 m/sx3,6 = 90 km/h, ou seja, 60 km/h e 90 km/h estão compreendidos entre 54 km/h e 90 km/h.

R- A

 

02-

Resumo dos gráficos do espaço, velocidade e aceleração do MUV, com a > 0 e com

a < 0.

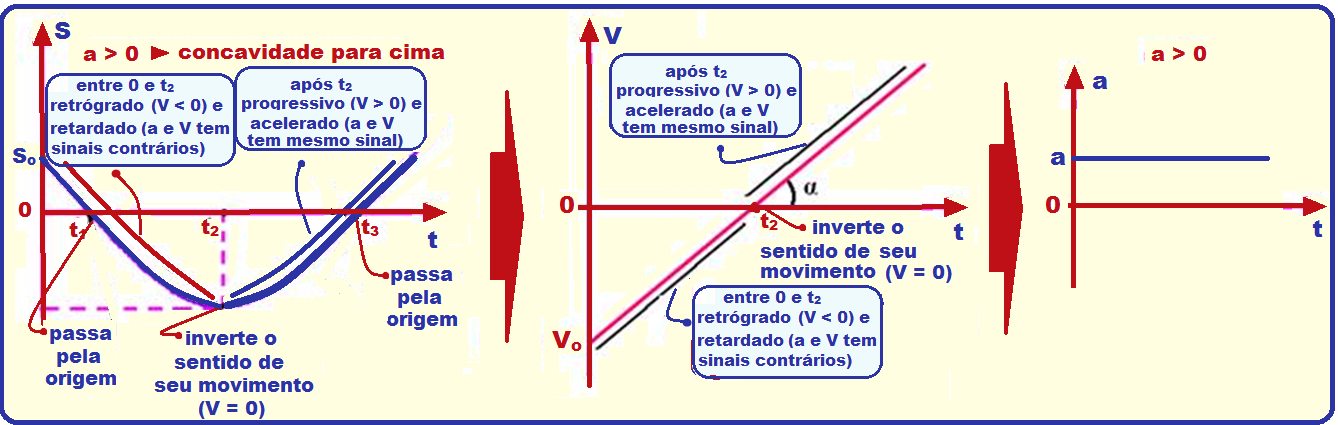
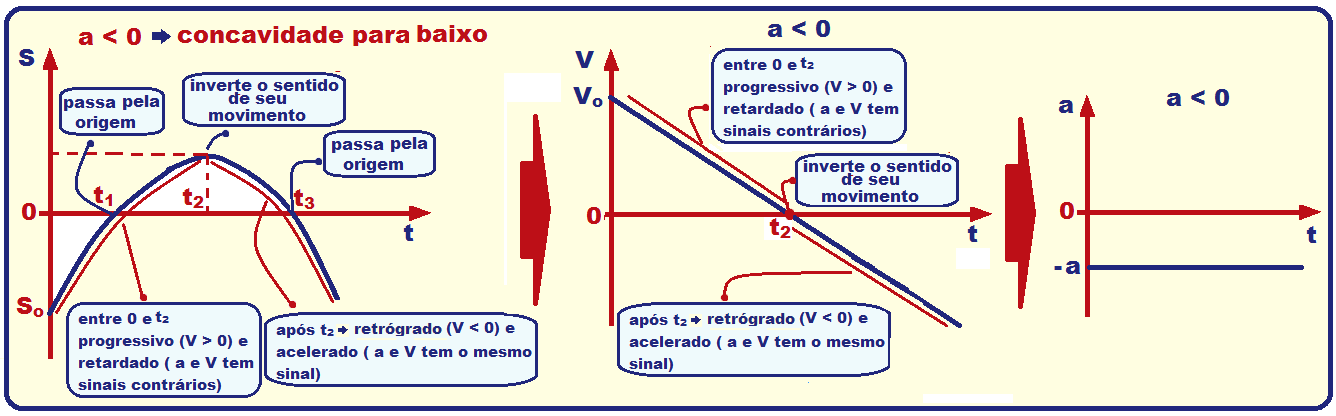R- D

03-

Forças que agem sobre cada bloco peso de B P_B = m_B.g = 20.10 = 200 N.

Parcela do peso de A responsável pela tendência de descida de A, paralela à superfície do plano inclinado P_pA = m_A.g.sen30^o = 400.10.1/2 = 200 N.

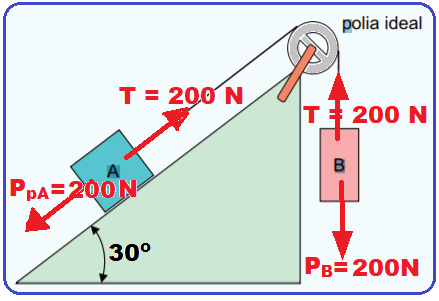
também de T = 200 N, sendo a força resultante sobre cada bloco nula e o sistema permanecerá em repouso.

R- A

04-

Colocando a origem das alturas no ponto Q e calculando a energia mecânica do corpo de massa m nos pontos P e Q:

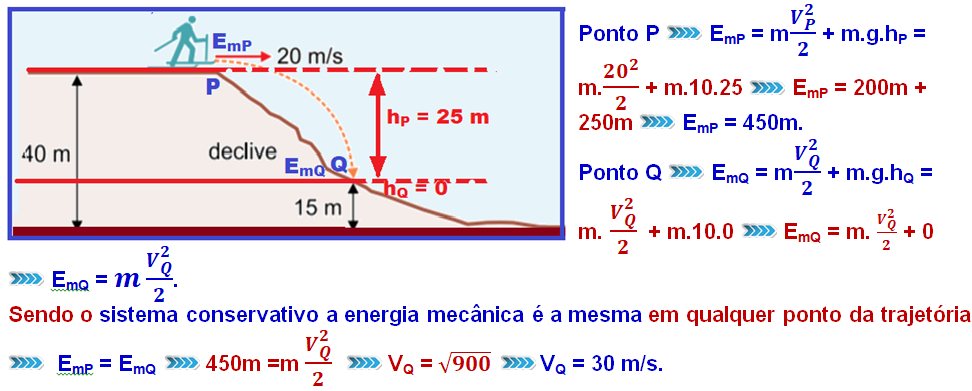
R- B

05-

Equação fundamental da calorimetria (calor sensível ou calor específico)

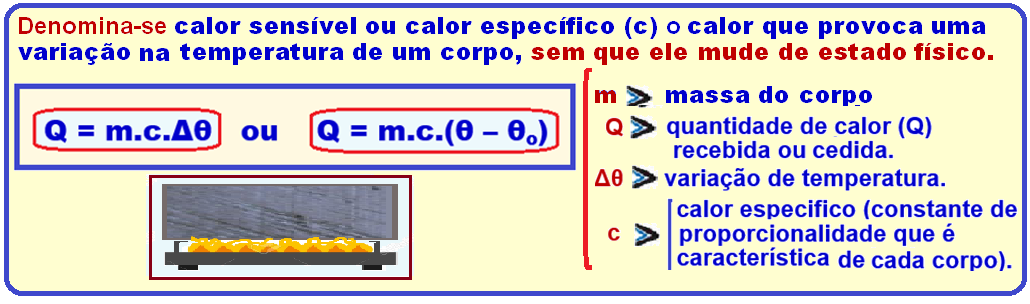
Princípio da Conservação da energia

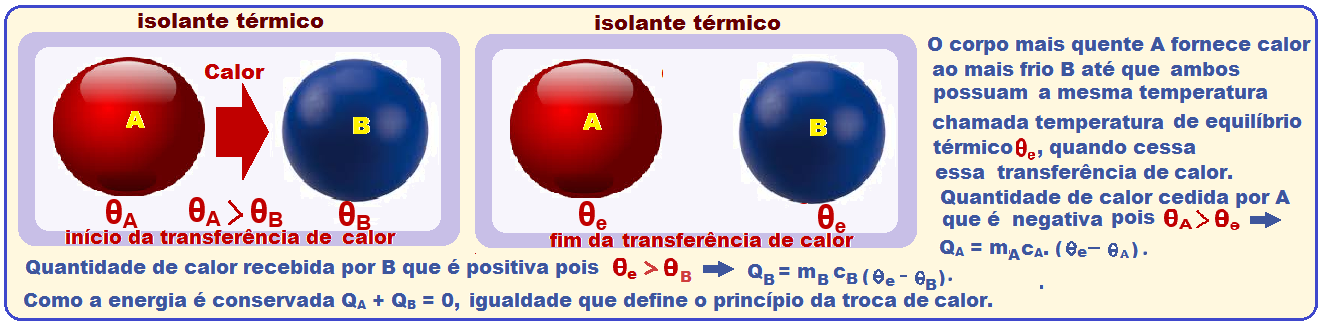
A teoria acima é válida para mais de um corpo e, como a quantidade de calor recebida é positiva e a cedida é negativa, tem-se que    Q1 + Q2 + Q3 + …. + QN  = 0  ou  m1.c1.(θe – θ1) + m2.c2.( θe – θ2) + m3.c3.( θe – θ3) + … + mN.cN.( θe – θN) = 0.

Enunciado desse princípio das trocas de calor:

Seja t_o a temperatura inicial do pedaço de ferro dentro do forno e no início da troca de calor com a água do calorímetro e, pelo enunciado m_água = m_ferro = m com t_equilíbrio = 80 ^oC e t_oágua = 20 ^oC.

Quantidade de calor recebido pela massa m de água Q_água = m.c_água (t_equilíbrio – t_oágua) = m.1.(80 – 20) Q_água = 60m.

Quantidade de calor cedido pela massa m ferro Q_ferro = m.c_ferro (t_equilíbrio – t_o) = m.0,12.(80 – t_o)

Q_ferro = 9,6m – 0,12mt_o.

Q_água + Q_ferr = 0 60m + 9,6m – 0,12mt_o = 0 t_o = 69,6m/0,12m t_o = 580 ^oC.

R- E

06-

R- B

07-

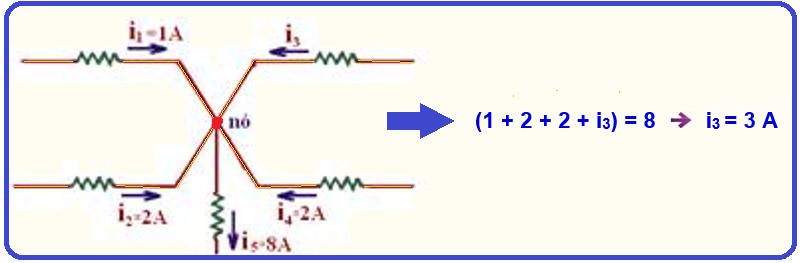
Primeira lei de Kirchhoff ou lei dos nós: “A soma algébrica das correntes que chegam a um nó é igual à soma algébrica das correntes que saem do mesmo nó”.

Exemplo numérico     determine a intensidade da corrente i3 do trecho de circuito abaixo:

 Segunda lei de Kirchhoff ou lei das malhas: “Percorrendo uma malha num mesmo sentido, é nula a soma algébrica das tensões encontradas em cada elemento do circuito”

Baseado na lei acima, escolhendo um sentido de percurso para cada malha, partindo de um ponto, retornando ao mesmo ponto e igualando esta soma algébrica de tensões a zero, você pode estabelecer as seguintes convenções:

 Convenção para o sinal de E:

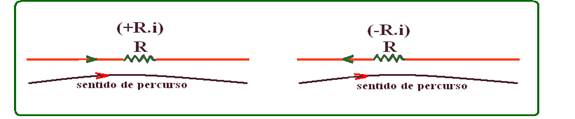
 Convenção para o sinal de R.i

Quando o sentido da corrente i coincidir com o sentido do percurso escolhido para a malha, o sinal de R.i será positivo e quando o sentido da corrente i não coincidir com o sentido de percurso escolhido para a malha, o sinal R.i será negativo.

Observe no ponto A que a corrente que chega i é a soma das correntes que saem, ou seja, i = 2 + 6 = 8 A.

Percorrendo a malha I no sentido horário a partir de A, retornando a A e igualando a zero – 8R – 0,5.2 + 5 = 0 8R = 4 R = 0,5 Ω.

Percorrendo a malha II no sentido horário a partir de A, retornando a A e igualando a zero + 6.3 –U + 0,5.8 = 0 U = 22 V.

R- D

08-

V_casca = V_caroço = V

d_casca = m_casca/V 0,4 = m_casca/V m_casca = 0,4V

d_caroço = m_caroço/V d_caroço = m_caroço/V m_caroço = d_caroço.V

d_corpo = m_corpo/V_corpo d_corpo = (m_casca + m_caroço)/2V d_corpo = (0,4V + d_caroço.V)/2V

R- C