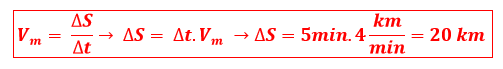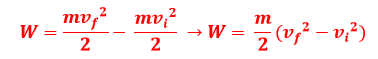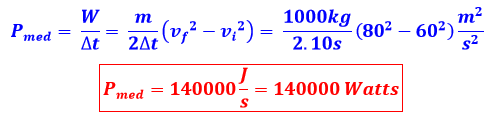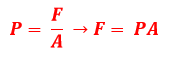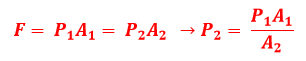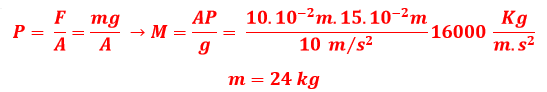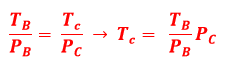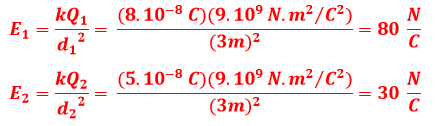FAMERP 2019 – Segunda Fase

Prova de conhecimentos específicos da Faculdade de Medicina de São José do Rio Preto (FAMERP) – 2019

A Faculdade de Medicina de São José do Rio Preto (FAMERP) é uma faculdade pública paulista, fundada em 1968.

É uma das 6 faculdades estaduais de Medicina de São Paulo e seu curso médico é ministrado no sistema tradicional.

Uma das mais bem conceituadas faculdades de Medicina e Enfermagem do país, se destaca por possuir o segundo maior hospital-escola do Brasil, o Hospital de Base de São José do Rio Preto, que perde apenas para o Hospital das Clínicas de São Paulo.

O Hospital de Base, tem instalações de aproximadamente 720 leitos. Mensalmente, o hospital realiza aproximadamente 4,5 mil internações e 2.600 cirurgias, além dos 35.000 atendimentos ambulatoriais e 12 mil atendimentos de emergência.

Em 2008, ganhou o prêmio nacional Guia do Estudante / Banco Real de Melhor Faculdade do Interior.

Ainda em 2008, recebeu nota máxima no Índice Geral de Cursos (IGC) promovido pelo MEC, classificando-se como a segunda melhor instituição pública do país, atrás apenas do ITA . No IGC 2009, divulgado no início de 2011, novamente a faculdade recebeu nota máxima do MEC .

A Comissão Permanente para o Vestibular (Comvest) da UNICAMP, era quem realizava a seleção para os cursos Medicina e Enfermagem da FAMERP até o ano de 2013, num sistema integrado ao vestibular da UNICAMP. Hoje esse processo é realizado pela VUNESP tendo agora a instituição o seu próprio processo seletivo.

Questão 1 – FAMERP – Conhecimentos específicos

Em uma competição automobilística, determinado piloto realiza 20 voltas na pista em 30 minutos.

a) Sabendo que o comprimento da pista é de 6,0 km, calcule a distância, em quilômetros, percorrida por esse piloto em 5,0 minutos, considerando que sua velocidade escalar média nesse intervalo de tempo seja igual à velocidade escalar média nas 20 voltas.

b) Nessa pista, há uma reta plana e horizontal. Durante a competição, determinado carro, com massa total 1000 kg, entra nessa reta com velocidade de 60 m/s e, depois de 10 segundos, chega ao seu final com velocidade de 80 m/s. Calcule a potência útil média, em watts, desenvolvida por esse carro nessa reta.

Questão 2 – FAMERP – Conhecimentos específicos

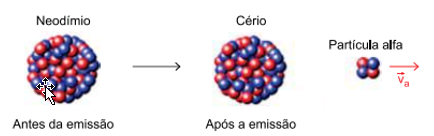
Um núcleo de neodímio, inicialmente em repouso, emite uma partícula alfa com velocidade v_a = 7,0 × 10⁶ m/s e se transforma em um núcleo de cério.

a) Sabendo que a massa do núcleo de cério é 35 vezes maior que a massa da partícula alfa, calcule o módulo da velocidade, em m/s, do núcleo de cério após a emissão da partícula alfa. Represente a direção e o sentido dessa velocidade, em relação à , por meio de um vetor.

b) Considerando que a massa de um próton e a massa de um nêutron tenham, cada uma delas, valor igual a 1,7 × 10^-27 kg e sabendo que a partícula alfa é formada por dois prótons e dois nêutrons, calcule a intensidade do impulso, em N·s, recebido pela partícula alfa durante sua emissão pelo núcleo de neodímio.

Questão 3 – FAMERP – Conhecimentos específicos

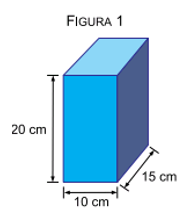
Um paralelepípedo reto-retângulo é apoiado sobre uma superfície plana, horizontal e lisa, primeiramente sobre a face de lados 10 cm e 15 cm, como mostra a figura 1. Nessa situação, a pressão que o paralelepípedo exerce sobre a superfície é 16000 Pa.

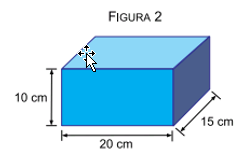
Posteriormente, o paralelepípedo é apoiado na mesma superfície, mas sobre a face de lados 15 cm e 20 cm, como mostra a figura 2.

a) Calcule a pressão, em pascals, que o paralelepípedo exerce sobre a superfície na situação da figura 2.

b) Ao ser colocado em um recipiente contendo água, cuja massa específica é 1,0 × 10³ kg/m³, esse paralelepípedo imerge até se apoiar no fundo do recipiente, que é plano e horizontal. Considerando a aceleração gravitacional igual a 10 m/s², calcule a força, em newtons, aplicada pelo fundo do recipiente no paralelepípedo.

Questão 4 – FAMERP – Conhecimentos específicos

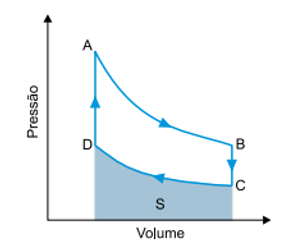
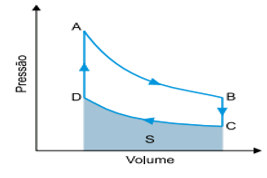
Um motor funciona obedecendo ao ciclo de Stirling, no qual um gás ideal é submetido a duas transformações isotérmicas, AB e CD, e a duas transformações isovolumétricas, BC e DA, como mostra a figura.

a) Sabendo que a temperatura do gás na transformação AB é 327 ºC e que a pressão nos pontos B e C valem 8,0 × 10⁵ Pa e 4,0 × 10⁵ Pa, respectivamente, calcule a temperatura do gás, em kelvins, durante a transformação CD.

b) Sabendo que a área S sob a curva da transformação CD, destacada na figura, corresponde a uma quantidade de energia igual a 3700 J, calcule a quantidade de calor, em joules, que o gás libera nessa transformação.

Questão 5 – FAMERP – Conhecimentos específicos

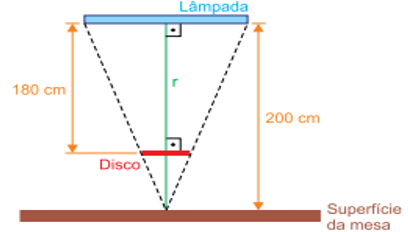
A figura mostra uma lâmpada retilínea, de comprimento 90 cm, fixa horizontalmente no teto de uma sala, 200 cm acima da superfície plana e horizontal de uma mesa. Um disco circular opaco foi colocado horizontalmente entre a lâmpada e a mesa, a 180 cm da lâmpada, sendo esta a maior distância para que ele não projete sombra sobre a mesa. A reta r, mostrada na figura, é vertical e passa pelo ponto médio da lâmpada e pelo centro do disco.

a) Calcule o diâmetro do disco, em centímetros.

b) Considere que o disco seja substituído por uma lente delgada, esférica e convergente, cujo eixo principal coincida com a reta r. Sabendo que essa lente foi colocada em uma posição em que projeta, sobre a superfície da mesa, uma imagem nítida da lâmpada quatro vezes menor que ela, calcule a distância focal da lente, em centímetros.

Questão 6 – FAMERP – Conhecimentos específicos

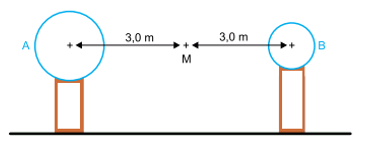
Duas esferas metálicas de dimensões diferentes, situadas no ar, são eletrizadas e colocadas sobre suportes isolantes com seus centros distando 6,0 metros entre si. As esferas são unidas com um fio condutor até que atinja o equilíbrio eletrostático, situação em que a esfera A fica eletrizada com carga positiva de valor 8,0 × 10^-8 C e a esfera B com carga também positiva de valor 5,0 × 10^-8 C.

a) Considerando que, para atingir o equilíbrio, 2,0 × 10¹¹ elétrons foram transferidos entre as esferas, que a carga de cada elétron é, em módulo, 1,6 × 10^-19 C e que o processo durou 4,0 × 10^-6 segundos, calcule a intensidade média da corrente elétrica, em ampères, que percorreu o condutor nesse intervalo de tempo.

b) Considerando a constante eletrostática do ar igual a 9,0 × 10⁹ (N · m²)/C², calcule a intensidade do campo elétrico, em N/C, resultante da ação das cargas elétricas das duas esferas no ponto M.

Respostas

1 – a) A velocidade média é dada por:

Sendo a distância percorrida e a quantidade de tempo necessária para o deslocamento.

Substituindo os valores dados do enunciado, e sabendo que a distância percorrida é o produto do comprimento da pista com o número de voltas, obtemos:

Utilizando a velocidade média obtida para encontrar a distância percorrida após cinco minutos:

b) A energia cinética é dada pela fórmula:

Em que E_C, m e v são a energia cinética, a massa e a velocidade do objeto, respectivamente.

O teorema de energia cinética-trabalho é representado por:

Substituindo E_C e E_I, obtemos:

A potência média é definida por:

Substituindo os valores fornecidos pelo enunciado, obtém-se:

2 – a) Por se tratar de um sistema em que não ocorrem forças externas, mas apenas forças internas, pode-se utilizar a conservação da quantidade de movimento:

Em que a quantidade de movimento é definida como o produto da velocidade de uma partícula por sua massa, conforme a expressão:

Como inicialmente o átomo está parado, = 0. O fator é dado pela soma das quantidades de movimento individuais do átomo e da partícula alfa resultantes. Portanto:

Em que M é a massa do Cério e m é a massa da partícula alfa. Substituindo na conservação da quantidade de movimento:

b) O impulso é definido como:

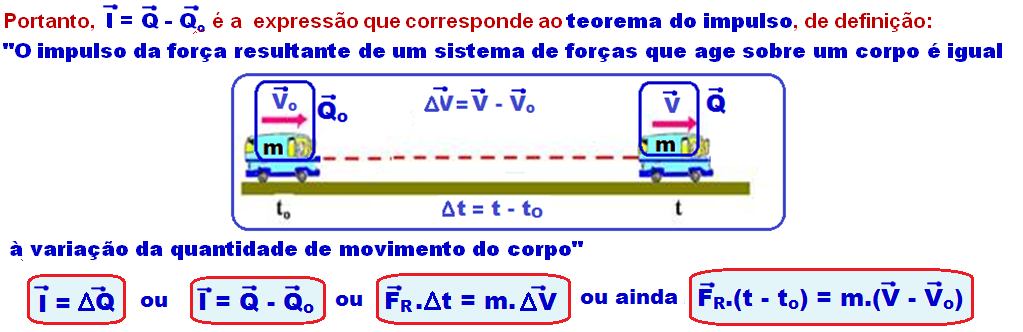Este impulso deve ser realizado com relação à partícula alfa. Assim como no item anterior, a quantidade de movimento inicial é nula. Portanto:

Substituindo os valores do enunciado, sabendo que a massa da partícula alfa é igual a soma da massa de dois prótons e dois nêutrons, e que a massa de prótons e nêutrons são iguais:

3 – a) A partir da definição de pressão, podemos escrever:

Sendo que a área A é a que está sujeita a força aplicada F. Repare que a força a qual a superfície está sujeita é a do peso do bloquinho:

No entanto, a massa do bloco não varia, logo, a força é constante para qualquer posicionamento do bloquinho, portanto:

Sendo e as áreas de contato da primeira e da segunda configuração, respectivamente. As áreas de contato têm a forma de retângulos, fazendo com que seus valores sejam o produto simples de uma dimensão pela outra. Substituindo os valores, obtemos:

b) Nesta situação, teremos três forças atuando no bloquinho, a força peso, a força normal à superfície e a força de empuxo exercida pelo fluído e contrária à força peso. O esboço abaixo retrata as três forças atuantes.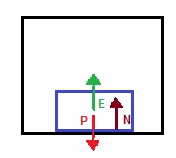

Aplicando a segunda lei de Newton e considerando que as forças que apontam para cima possuem sinal negativo, teremos:

Porém, o bloquinho encontra-se parado, logo possui aceleração nula, logo:

A força peso é o produto da massa do objeto pela aceleração gravitacional:

A força de empuxo é dada por:

Em que V é o volume de líquido deslocado, é a densidade do líquido e g é a aceleração gravitacional. Pelo princípio de Arquimedes, o volume de líquido deslocado é igual ao volume do objeto submerso no líquido.

Usando as equações e o princípio de Arquimedes, obtemos:

A massa do bloquinho pode ser obtida utilizando o conceito de pressão apresentado no item a, utilizando a pressão e a área da primeira configuração, tal que:

Substituindo na equação da força normal:

4 – a) Por tratar-se de um gás ideal, podemos utilizar a lei de Clapeyron:

Onde P, V, T e n são, respectivamente, pressão, volume, temperatura e número de mols do gás. R é a constante universal dos gases. Do enunciado e da figura, temos que AB e CD são transformações isotérmicas, DA e BC transformações volumétricas.

Nos pontos B e C os volumes são constantes, fazendo com que a equação de Clapeyron se torne:

Aplicando a relação T/P nos pontos B e C:

Substituindo os valores do enunciado, transformando a temperatura da isotérmica AB de Celsius para Kelvin e sabendo que a curva CD é isotérmica (mesma temperatura):

b) A primeira lei da termodinâmica é dada por:

Sendo Q a energia fornecida para o gás, W o trabalho exercido pelo gás e a energia interna armazenada pelo gás. Como a curva é isotérmica, deve ser nulo, visto que:

O trabalho W é dado pela área abaixo da curva no diagrama PxV dada no enunciado, logo, a energia interna é:

5 – a) Observando a figura, é possível observar que há uma semelhança de triângulos:

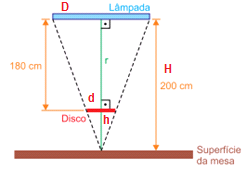
Por semelhança de triângulo, podemos determinar o diâmetro do disco, dividindo a base do triângulo menor pela do maior, e a altura do triângulo menor pela do triângulo maior:

b) A lente convergente pode estar posicionada em qualquer lugar entre a lâmpada D e o anteparo d, de forma que nos convém montar um esboço do problema:

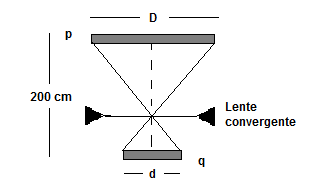
6 – a) A corrente média é definida como a variação de carga sobre um intervalo de tempo. A variação da carga elétrica total é o número de elétrons que fluiu de uma esfera até a outra multiplicada pela carga elétrica fundamental do elétron:

Substituindo a última equação na primeira, e colocando os valores dados no enunciado, chegamos em:

b) O campo elétrico é dado pela relação:

Em que k é a constante eletrostática do meio (neste caso é a do ar), Q é o valor da carga geradora e d é a distância da carga geradora ao ponto em que queremos conhecer o valor do campo.

Repare que teremos dois campos atuando no ponto M relacionados às esferas 1 e 2. Utilizando a fórmula do campo elétrico para as esferas teremos:

Para encontrar o campo elétrico total no ponto M, devemos observar o vetor dos campos elétricos das esferas individualmente, respeitando a seguinte constatação:

Objetos com carga positiva possuem suas linhas de campo apontando para fora.
Objetos com carga negativa possuem suas linhas de campo apontando para dentro.

Logo abaixo há uma ilustração de como as linhas de campo se comportam para objetos redondos carregados.

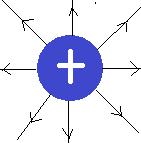
Aplicando este conceito na figura, temos:

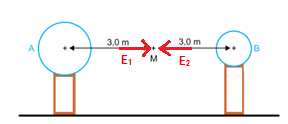
Como os campos estão opostos um ao outro no ponto M, o módulo do campo total nesse ponto será dado pela diferença entre os dois, tal que: