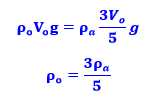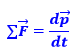ESCOLA NAVAL CPAEN/2018/2019

CONCURSO PÚBLICO DE ADMISSÃO À ESCOLA NAVAL CPAEN/2018/2019

A Escola Naval é considerada a mais antiga Instituição de ensino superior do País e é a academia militar formadora de oficiais de carreira da Marinha do Brasil, nas modalidades de oficial de armada, de intendência ou fuzileiro naval. A Escola Naval tem duas formas de admissão de alunos: processo seletivo direto (PSAEN – Processo Seletivo de Admissão à Escola Naval) ou a entrada por meio do Colégio Naval.

A Escola Naval está localizada na Ilha de Villegagnon, na cidade do Rio de Janeiro. O processo seletivo é composto de duas fases, com provas de matemática, português, inglês e física. Embora voltado para o Ensino Médio, uma peculiaridade do concurso é a presença de alguns conteúdos de Ensino Superior, como o Cálculo Diferencial e Integral, cobrado na matemática.

A duração do curso é de 4 anos, em regime interno e na condição de Aspirante. Após o término do curso, o aluno é promovido a Guarda-Marinha. Após a viagem de instrução, será nomeado Oficial no posto de 2º Tenente.

Requisitos de Inscrição

Os principais requisitos para os candidatos, exclusivamente do sexo masculino são:

Idade: mais de 18 anos e menos de 23 anos de idade na data prevista para o início do curso;

Ser brasileiro nato e ter concluído, com aproveitamento, o Ensino Médio ou estar em fase de conclusão;

Estado Civil: ser solteiro, nunca haver vivido em concubinato ou

união estável e não ter filhos.

Questão 1 – Escola Naval 2018/2019

Analise a figura abaixo

.

A figura acima mostra um objeto flutuando na água contida em um vaso sustentado por duas molas idênticas, de constante elástica desconhecida. Numa situação de equilíbrio, em que esse vaso de massa desprezível, contém somente a água, as molas ficam comprimidas de x. Quando o objeto, cujo volume é 1/30 do volume da água, é inserido no vaso, as molas passam a ficar comprimidas de x’. Sabendo que, no equilíbrio, 60% do volume do objeto fica submerso, qual a razão x’/x?

(A) 1,06

(B) 1,05

(C) 1,04

(D) 1,03

(E) 1,02

Questão 2 – Escola Naval 2018/2019

Analise a figura abaixo.

A figura acima mostra uma espira retangular, de lados a=40 cm e b=20 cm, no instante t=0. Considere que a espira se move com velocidade v=5,0 cm/s, para a esquerda, perpendicularmente a um campo magnético uniforme de indução, B=2,0 T. Sabendo que a espira tem uma resistência de 20 Ω, qual é a intensidade, em ampère, da corrente elétrica na espira em t=3,0 s?

(A) 1,0.10^-3

(B) 2,0.10^-3

(C) 3,0.10^-3

(D) 1,0.10^-2

(E) 2,0.10^-2

 

Questão 3 – Escola Naval 2018/2019

Analise o gráfico abaixo.

Em uma série de experiências, foi medido, para três valores do comprimento L, o período de oscilação correspondente a meio comprimento de onda estacionária entre as extremidades fixas de uma corda com densidade linear de massa 0,60 kg/m. Os resultados, representados no gráfico (linear) da figura acima, indicam que a tensão na corda, em newtons, em todas as experiências realizadas, foi igual a:

(A) 60

(B) 45

(C) 30

(D) 20

(E) 15

 

Questão 4 – Escola Naval 2018/2019

Analise as afirmativas abaixo, que se referem às grandezas impulso e quantidade de movimento.

I- Se uma partícula está submetida a uma força resultante constante, a direção da quantidade de movimento da partícula pode mudar.

II- Se uma partícula está se movendo em círculo com módulo da velocidade constante v, a intensidade da taxa de variação da quantidade de movimento no tempo é proporcional a v².

III- Com o gráfico do módulo da força resultante que atua sobre uma partícula em função da posição x, pode-se obter o módulo do impulso sobre a partícula, calculando-se a área entre a curva e o eixo x.

IV- Se J representa o impulso de uma determinada força, então ΔJ/Δt representa a variação da força. Assinale a opção correta.

(A) Apenas as afirmativas I e II são verdadeiras.

(B) Apenas as afirmativas I e III são verdadeiras.

(C) Apenas as afirmativas III e IV são verdadeiras.

(D) Apenas as afirmativas I, II e IV são verdadeiras.

(E) Apenas as afirmativas II, III e IV são verdadeiras.

 

Questão 5 – Escola Naval 2018/2019

Analise a figura abaixo.

A figura mostra um pêndulo cônico no qual um pequeno objeto de massa m, preso à extremidade inferior de um fio, move-se em uma circunferência horizontal de raio R, com o módulo da velocidade constante. O fio tem comprimento L e massa desprezível. Sendo g a aceleração da gravidade e sabendo que a relação entre a tração T e o peso P do objeto é T=4P, qual o período do movimento?

(A)

(B)

(C)

(D)

(E)

 

Questão 6 – Escola Naval 2018/2019

Analise o diagrama PV abaixo.

A figura acima exibe, num diagrama PV, um ciclo reversível a que está submetido 2 moles de um gás monoatômico ideal. Sabendo que as temperaturas nos estados A, B e C estão relacionadas por T_C = 3T_B = 9T_A, qual a eficiência do ciclo?

(A) 1/3

(B) 1/5

(C) 1/6

(D) 1/7

(E) 1/9

Questão 7 – Escola Naval 2018/2019

Analise a figura abaixo.

Diferenças de potencial de 30 volts já representam, para alguns indivíduos, risco de fibrilação induzida (mesmo que o choque elétrico seja de baixa corrente). Suponha que uma força eletromotriz aplicada entre as mãos de um ser humano seja, de modo simplificado, equivalente ao circuito mostrado na figura acima, com a magnitude da tensão V₀ no capacitor (coração) determinando o grau de risco. Se a fem é de 30 volts, a potência elétrica, em watts, dissipada no corpo humano é igual a:

(A) 0,9

(B) 0,6

(C) 0,5

(D) 0,3

(E) 0,2

 

Questão 8 – Escola Naval 2018/2019

Analise a figura abaixo.

Conforme indica a figura acima, uma bolha de hélio sofre um deslocamento vertical na água, do ponto A até o ponto B, onde AB = 10m. Sabendo que a razão (v_B / v_A) entre os volumes é dobro da razão (T_B/T_A) entre as temperaturas. Qual a pressão, em pascal, no ponto B?

Dado: massa específica da água 103 kg/m³ e g=10 m/s²

(A) 1.10³

(B) 2.10⁴

(C) 1.10⁴

(D) 2.10⁵

(E) 1.10⁵

 

Questão 9 – Escola Naval 2018/2019

Analise a figura abaixo.

A figura acima mostra uma casca esférica de raio interno a e raio externo 4a, ambos em metros, carregada com densidade volumétrica de carga p=2/a³ (C/m³). No centro geométrico da casca, há uma carga pontual q= -379 C. Estando o sistema de cargas descrito acima isolado numa região de vácuo, qual o módulo, a direção e o sentido do vetor campo elétrico, em newtons/coulomb, nos pontos do espaço que distam 5a metros da carga pontual?

Dados: a é um número inteiro positivo, k₀ é a constante elétrica no vácuo, considere π = 3

(A) 5k₀ / a², radial para dentro.

(B) 5k₀ / a², radial para fora.

(C) 25k₀ / a², tangencial no sentido anti-horário.

(D) 25k₀ / a², radial para fora.

(E) 25k₀ / a², tangencial no sentido horário.

 

Questão 10 – Escola Naval 2018/2019

Analise a figura abaixo

Na figura acima, a linha pontilhada mostra a trajetória plana de uma partícula de carga -q = -3,0 C que percorre 6,0 metros, ao se deslocar do ponto A, onde estava em repouso, até o ponto B, onde foi conduzida novamente ao repouso. Nessa região do espaço, há um campo elétrico conservativo, cujas superfícies equipotenciais estão representadas na figura. Sabe-se que, ao longo desse deslocamento da partícula, atuam somente duas forças sobre ela, onde uma delas é a força externa, F_ext. Sendo assim, qual o trabalho, em quilojoules, realizado pela força F_ext no deslocamento da partícula do ponto A até o ponto B?

(A) -0,28

(B) +0,28

(C) -0,56

(D) +0,56

(E) -0,85

 

Questão 11 – Escola Naval 2018/2019

Analise a figura abaixo

A figura acima mostra um tubo de 1,0 m de comprimento, aberto nas extremidades e em repouso. Considere que o terceiro harmônico é produzido no tubo e parte do som que escapa é captado no detector D, que se afasta em linha reta. Qual é a razão, v_D/v_s, entre a velocidade do detector, v_D, e a velocidade do som, v_s, para que a frequência do som captado seja igual à frequência fundamental do tubo?

(A) 1/3

(B) 1/2

(C) 3/5

(D) 3/4

(E) 2/3

 

Questão 12 – Escola Naval 2018/2019

Analise os gráficos abaixo.

Uma partícula executa um movimento, ao longo de uma trajetória retilínea, descrito pelos gráficos acima. Estando todas as unidades no sistema internacional, com relação à descrição desse mesmo movimento, assinale a opção que completa corretamente as lacunas da sentença abaixo.

 

Questão 13 – Escola Naval 2018/2019

Analise a figura abaixo.

Para que um galvanômetro ideal G (resistência nula), o qual suporta uma corrente máxima l_Gm. seja utilizado em um simples amperímetro capaz de indicar qualquer valor de corrente, são utilizadas as resistências R_s (shunt, em paralelo com G) e R_G (em série com G), como mostra o circuito da figura acima. Considere que, medindo uma corrente I=50,5 A utilizando esse amperímetro, o galvanômetro apresenta sua deflexão máxima indicando 50,0 A, com l_G=l_Gm=500mA. Sendo assim, a razão R_G/R_S utilizada nessa medida vale:

(A) 15,0

(B) 30,0

(C) 75,0

(D) 100

(E) 150

 

Questão 14 – Escola Naval 2018/2019

Analise a figura abaixo.

Suponha que uma descarga atmosférica (raio) transferiu cargas positivas da nuvem para o solo de acordo com o gráfico da corrente elétrica (em quiloamperes) em função do tempo (em microssegundos) mostrado na figura acima. Com uma duração de apenas 60μs, esse fenômeno transferiu ao solo uma carga elétrica total, em coulombs, de:

(A) 1,9

(B) 1,4

(C) 0,96

(D) 0,26

(E) 0,13

 

Questão 15 – Escola Naval 2018/2019

Analise a figura abaixo.

A figura acima mostra a seção reta longitudinal de uma caçamba rígida preenchida com troncos de madeira e apoiada sobre o plano inclinado de θ° por meio de pés retangulares transversais distantes D=3,0 m um do outro. O equilíbrio estático da caçamba é mantido utilizando vários calços fixos. Considere o centro de massa CM distante h=1,0 m do plano inclinado e equidistante dos pontos A e B nos quais estão aplicadas as resultantes das forças de contato, sendo A, B e CM pertencentes ao mesmo plano perpendicular ao plano inclinado. Desprezando o atrito, na iminência de a caçamba tombar (reação normal N_B=0), a tangente do ângulo θ vale:

(A) 2,0

(B) 1,5

(C)

(D)

(E) 0,50

Questão 16 – Escola Naval 2018/2019

Analise a figura abaixo.

A figura acima mostra um pêndulo oscilando em movimento harmônico simples. Sua equação de posição angular em função do tempo é dada por: θ(t)=(π/30)sen(ωt) radianos. Sabe-se que L=2,5 m é o comprimento do pêndulo, e g=10 m/s² é a aceleração da gravidade local. Qual a velocidade linear, em m/s, da massa m=2,0kg, quando passa pelo ponto mais baixo de sua trajetória?

Dado: considere π=3

(A) 0,30

(B) 0,50

(C) 0,60

(D) 0,80

(E) 1,0

 

Questão 17 – Escola Naval 2018/2019

Considere um bloco de gelo de 80,0 kg deslizando, com velocidade constante v, em um plano inclinado de 30° com a horizontal. Sabendo que a massa de gelo que derrete por minuto, em consequência do atrito, é de 20,0 g, e que o calor latente de fusão do gelo é 336 J/g, qual o valor da velocidade v, em centímetros por segundo?

Dado: g=10 m/s²

(A) 4,20

(B) 16,8

(C) 20,4

(D) 28,0

(E) 32,0

 

Questão 18 – Escola Naval 2018/2019

Analise a figura abaixo.

A figura acima mostra um sistema isolado de três partículas de massa m, ocupando os vértices de um triângulo equilátero inscrito em uma circunferência de raio R. Nessa configuração, a energia potencial gravitacional é U₀. Considerando que a energia potencial gravitacional é nula no infinito, se o raio é reduzido à metade, qual é a razão entre variação da energia potencial gravitacional do sistema e a energia potencial gravitacional inicial, ΔU/U₀?

(A)

(B)

(C) 1

(D)

(E) 2

 

Questão 19 – Escola Naval 2018/2019

Uma cabine de elevador de massa M é puxada para cima por meio de um cabo quando, de seu teto,

se desprende um pequeno parafuso. Sabendo que o módulo da aceleração relativa do parafuso em relação à cabine é de 4/5 g, onde g é o módulo da aceleração da gravidade, qual a razão entre o módulo da tração T no cabo e o peso P da cabine, T/P?

(A) 1/2

(B) 2/3

(C) 3/4

(D) 4/5

(E) 1

 

Questão 20 – Escola Naval 2018/2019

Analise a figura abaixo.

Considere duas ondas planas, uma de luz visível e outra de som audível, oscilando com comprimento de onda iguais a λ_L=10^-4 cm e λ_s=1,7 cm, respectivamente. No mesmo instante, ambas incidem perpendicularmente sobre um mesmo lado do anteparo plano, opaco e bom absorvente acústico mostrado na figura acima. Atravessando o orifício circular de diâmetro d pode-se afirmar que, na região do outro lado do anteparo:

(A) apenas a onda sonora pode ser detectada se d << 1,7 cm, devido à difração.

(B) apenas a onda luminosa pode ser detectada se d << 1,7 cm, devido à refração.

(C) a propagação das duas ondas é aproximadamente retilínea se d >> 1,7 cm.

(D) a propagação das duas ondas é aproximadamente esférica se d >> 1,7 cm.

(E) nenhuma das ondas pode ser plana.

 

Respostas

 

Questão 1

Em primeiro lugar, deve-se encontrar a relação entre as densidades do objeto e da água utilizando a fórmula para a força de empuxo E realizada em um corpo com um volume submerso V_s no fluído de densidade ρ, sendo esse empuxo calculado como

Como o corpo de densidade ρ_o e volume total V_o está em equilíbrio, a força de empuxo sobre o corpo será igual a força peso, utilizando ρ_a para denotar a densidade da água e usando que o volume de água deslocado pelo fluído V_s é 3/5 do volume do objeto V_o (60%), temos:

Questão 2

Primeiro usamos a fórmula para calcular o fluxo Φ_B de um campo magnético uniforme B passando por uma área A:

A área mencionada acima é a área do retângulo por onde passa o campo magnético, como apenas uma parte da espira está sobre o campo, dizemos que a área é então o produto do lado b por um comprimento x que depende do tempo, pois conforme a espira se move para dentro do campo, esse x aumenta, assim a relação acima se torna:

Questão 3

Devemos utilizar aqui a fórmula para uma onda que se propaga com velocidade v em uma corda de densidade linear µ e no qual é aplicada uma tensão T:

Usamos também que a velocidade v na corda está relacionada com o comprimento de onda λ e a frequência linear de oscilação f:

Questão 4

I – Devemos verificar essa afirmativa utilizando a segunda Lei de Newton, que relaciona a força resultante sobre um corpo (soma de todas as forças sobre esse) e a variação do momento:

Assim, se o termo da força resultante for diferente de zero e apontar em uma direção diferente do momento inicial p, a direção do momento irá mudar, portanto é verdadeira a afirmativa.

 

II – Verdadeira, pois a fórmula da força centrípeta é

Ou seja, a força é proporcional a v², sendo assim, pela segunda Lei de Newton, a taxa de variação do momento também será proporcional à v².

 

III – Falsa, uma vez que a área sob a curva de um gráfico de Posição x Força resulta no trabalho realizado na partícula pela força. O impulso é dado pela área em um gráfico de Tempo x Força.

 

 

Questão 5

O primeiro passo, nesse problema, é encontrar a componente da tensão que funciona como força centrípeta para manter o objeto no círculo.

Visualizando a figura acima, o cateto que buscamos é o adjacente, então a componente do vetor de força da tensão que está na direção desejada é 4Pcosθ. Igualamos então esse termo à expressão força centrípeta:

Questão 6

Podemos calcular a eficiência η da máquina como a razão entre o trabalho W realizado pela máquina e o calor Q inserido nela:

O trabalho realizado se obtém através da área compreendida dentro do ciclo triangular, logo, obtemos o trabalho como

Já o calor inserido deve ser calculado sobre as trajetórias de A a B e de B a C, pois é onde a temperatura aumenta. Como o gás é ideal e monoatômico, convém relembrar algumas relações para esse tipo de gás utilizando o número de mols n e a constante dos gases ideais R:

Questão 7

A ideia principal nesse problema é lembrar que o capacitor funciona como um circuito aberto em corrente contínua, assim não haverá passagem de corrente na malha em que o capacitor se encontra, inutilizando o resistor que se encontra ali. A corrente I que flui pelo circuito é então apenas a que passa na malha em que se encontra a fonte U=30 V e a resistência restante R, o circuito equivalente com essas modificações é exibido na imagem abaixo.

Questão 8

A fórmula que relaciona a pressão no ponto A (mais baixo) e a pressão no ponto B (mais alto) é

No qual ρ é massa específica da água, g é a aceleração da gravidade e Δh é a diferença de altura entre os pontos. Para substituir a pressão P_A nessa relação, recorremos a equivalência dada no enunciado:

Questão 9

Como o enunciado pede o campo elétrico fora da casca esférica, podemos usar o princípio da superposição, que diz que o campo E₁ fora da casca esférica será igual a soma de um campo E_4a gerado por uma esfera de raio 4a carregada positivamente e de outro campo E_a gerado por uma outra esfera de raio a carregada negativamente, ambas posicionadas no mesmo centro:

No qual k₀ é a constante elétrica no vácuo. Caso o campo dê positivo, ele é radial para fora, enquanto que se for negativo, é radial para dentro. Essa mesma fórmula pode ser usada para as esferas de carga Q e de qualquer raio R, porém foi dada a densidade volumétrica de carga ρ ao em vez da carga elétrica Q, devemos então fazer a conversão utilizando a definição de densidade de carga, que é a carga dividida pelo volume:

O campo total E será então a soma de todos os campos calculados:

Questão 11

Primeiro devemos relembrar a fórmula do efeito Doppler para uma fonte de ondas se afastando a uma velocidade v_s de um receptor que se move a uma velocidade v_r, a relação entre a frequência medida pela fonte (f_s) e e medida pelo receptor (f_r) é dada por:

Questão 12

Se um corpo possui uma aceleração linear dada como

 

Questão 13

Considerando o galvanômetro ideal, podemos utilizar a fórmula do divisor de corrente para calcular a razão pedida. O divisor de corrente diz que a corrente em um ramo I_G será proporcional à corrente de entrada na malha I por um fator de resistência dado por:

 

Questão 14

Para um gráfico de Tempo x Corrente linear, vale a seguinte relação:

 

Questão 15

Para resolver esse problema, utilizaremos uma equação parecida com a da segunda Lei de Newton, mas para o caso rotacional que relaciona o torque externo τ resultante aplicado à um corpo com seu momento de inércia I e sua aceleração angular α:

Essa distância d entre o eixo de giro e a reta que passa pelo vetor de força é denominada de braço. No caso desse problema a caçamba tende a girar em torno do ponto A, por isso devemos impor que a aceleração angular em volta desse ponto deve ser zero pois ainda está na iminência de tombar. O braço das forças N_A, F_A e F_B em relação ao ponto A é zero, enquanto N_B possui módulo zero, por isso o torque de todas essas forças é zerado, restando apenas o da força peso. A força peso deve ser decomposta em duas componentes antes de se calcular o braço, uma perpendicular e outra paralela ao plano inclinado.

A decomposição acima mostra que o braço até a componente paralela é h, então o primeiro torque, que ocorre no sentido anti-horário, é:

 

Questão 16

Temos que

No qual A representa a amplitude do deslocamento linear formado pelo pêndulo (assim como representa a amplitude do deslocamento linear do bloco presa por uma mola), usamos a seguinte fórmula do comprimento de arco para trocar o A pela amplitude do movimento angular Θ que possuímos:

Questão 17

Onde foi usada a definição de velocidade constante. Agora deve-se desenhar o diagrama de corpo livre para o bloco descendo o plano inclinado:

Questão 18

Utilizando a Lei dos cossenos podemos calcular a distância L em termos da distância R, o triângulo escolhido para se fazer a análise é exibido abaixo:

 

Questão 19

Primeiro escrevemos a expressão da aceleração do parafuso para diferentes referenciais:

Questão 20

As ondas vão incidir sobre o anteparo e serão detectadas do outro lado, se d for muito menor que o comprimento de onda de ambas, a onda de saída será aproximadamente esférica, enquanto que se tivermos d muito maior que o comprimento de onda de ambas, a onda de saída continuará aproximadamente plana e retilínea. Portanto, a resposta correta é a alternativa C.

Clique aqui para ver sobre o tema!

Confira as vídeo aulas!