Resolução comentada das questões de FÍSICA da Escola Naval – 2018/2017
Resolução comentada das questões de FÍSICA da
Escola Naval – 2018/2017
01-
Fragata Independência
Ela se desloca para o norte com velocidade de VI = 15√2 nós e a correnteza tem na direção norte-sul

e velocidade de 2 nós.
Assim a velocidade relativa da fragata Independência em relação ao farol (vista por uma pessoa no farol) será VRI = (15√2 – 2) nós, no sentido sul-norte.
Fragata Rademaker
Na sequência abaixo, o ângulo entre o nordeste e o norte e o leste é de 45o e assim, você decompõe a velocidade VR = 20√2 nós em sua parcelas vertical e horizontal, cada uma de intensidade Vv = Vh 
VR.cos45o = 20.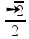
![]() Vv = Vh = 10
Vv = Vh = 10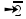 nós.
nós.
Em seguida, considerando a velocidade relativa apenas na vertical, onde você tem Vc = 2 nós (sul), a parcela Vv deverá ter intensidade Vv = (10√2 – 2) nós (norte).
Então, a fragata Rademaker se desloca ao mesmo tempo com velocidades de direção e sentidos indicados na última figura acima.
Cálculo do módulo da velocidade relativa da Fragata Independência, em nós, em relação à Fragata Rademaker, analisando a sequência de figuras abaixo:
Na figura I você tem a velocidade resultante horizontal e vertical final de cada fragata, vistas por um observador no farol. Na figura II só as componentes verticais de cada uma e, como elas se movem no mesmo sentido a velocidade relativa final V’v na direção vertical será a diferença entre

essas velocidades ![]() V’v = (15√2 – 2) – (10√2 – 2) = 15√2 – 2 – 10√2 + 2
V’v = (15√2 – 2) – (10√2 – 2) = 15√2 – 2 – 10√2 + 2 ![]() V’v = 5√2 nós.(figura III).
V’v = 5√2 nós.(figura III).
Na direção horizontal a velocidade é apenas a da fragata Rademaker de sentido oeste-leste e
intensidade V’h = 10√2 nós.
Para o cálculo do módulo da velocidade relativa pedida você deve aplicar Pitágoras na soma

vetorial acima ![]() V’2 = (5√2)2 + (10√2)2 = 25.2 + 100.2 = 50 + 200
V’2 = (5√2)2 + (10√2)2 = 25.2 + 100.2 = 50 + 200 ![]() V’2 = √250 = 15,81 nós.
V’2 = √250 = 15,81 nós.
R- D
02- Colocando as forças que agem sobre o sistema e calculando o momento de cada força com o
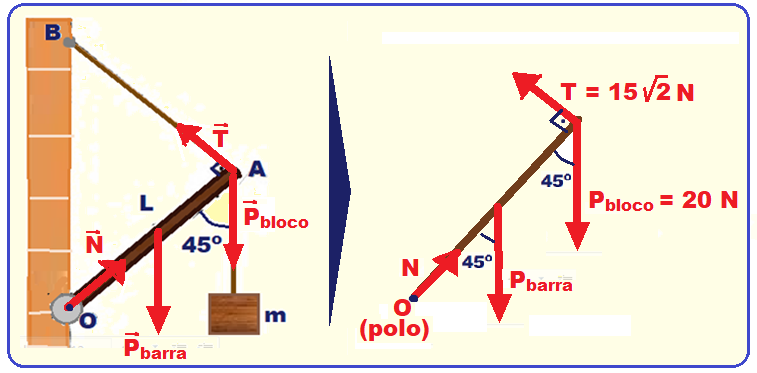
polo em O, sendo dados ![]() T = 15√2 N; Pbloco = mg = 2.10 = 20 N; L = 5,0 m; peso da barra Pbarra e estabelecendo o sentido horário de rotação em torno de O como positivo e lembrando que d é a distância entre o prolongamento da força e o polo:
T = 15√2 N; Pbloco = mg = 2.10 = 20 N; L = 5,0 m; peso da barra Pbarra e estabelecendo o sentido horário de rotação em torno de O como positivo e lembrando que d é a distância entre o prolongamento da força e o polo:
![]() Momento da força peso do bloco
Momento da força peso do bloco
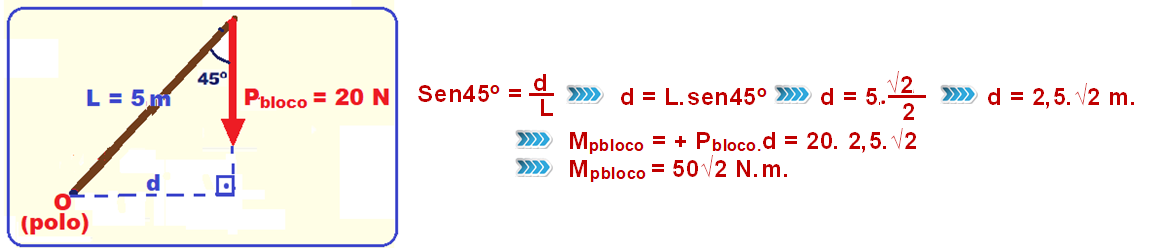
![]() Momento da força de tração
Momento da força de tração

![]() Momento da força peso da barra
Momento da força peso da barra

![]() Momento da força normal
Momento da força normal


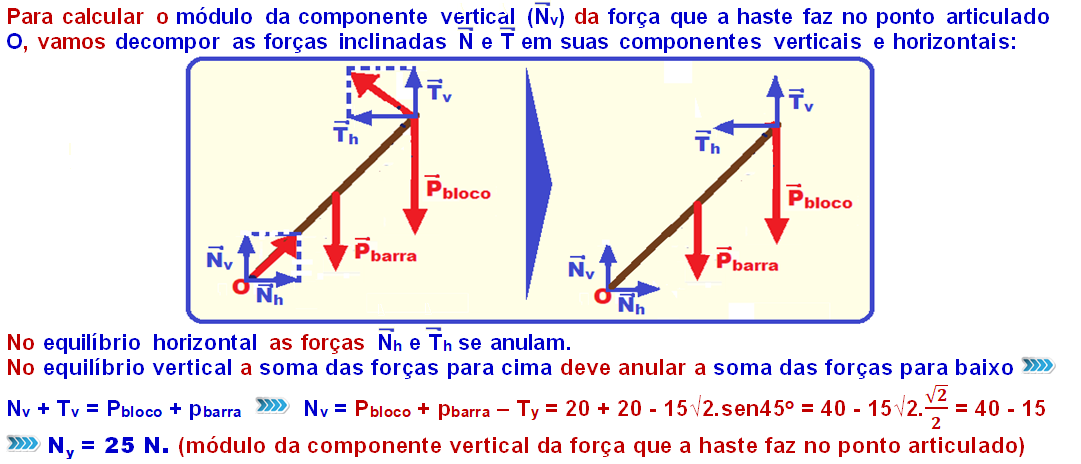
R- C
03- Como não pode haver escorregamento entre o bloco e a plataforma você deve utilizar o coeficiente de atrito estático máximo 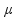 e (bloco e plataforma estão em contato, mas não deslizam, estão na iminência de deslizar)
e (bloco e plataforma estão em contato, mas não deslizam, estão na iminência de deslizar)
Massa do bloco ![]() mb = 12 kg
mb = 12 kg ![]() massa da plataforma
massa da plataforma ![]() mp = 3 kg
mp = 3 kg ![]()
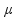 e = 0,3
e = 0,3
Observe que bloco e plataforma constituem um único sistema sujeito a uma força de intensidade F, horizontal e para a direita, fazendo com que esse sistema se mova para a direita, pois a superfície horizontal em que está apoiada não oferece atrito.
A força que age sobre o sistema (bloco + plataforma) provoca uma aceleração de intensidade a tal
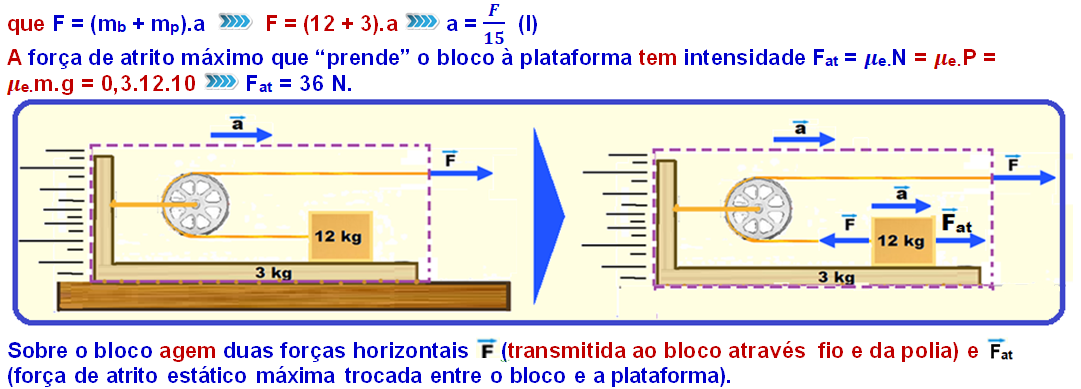
Como o bloco (e todo o sistema) se move para a direita a força resultante sobre ele terá intensidade FR = mbloco.a, horizontal e para a direita.

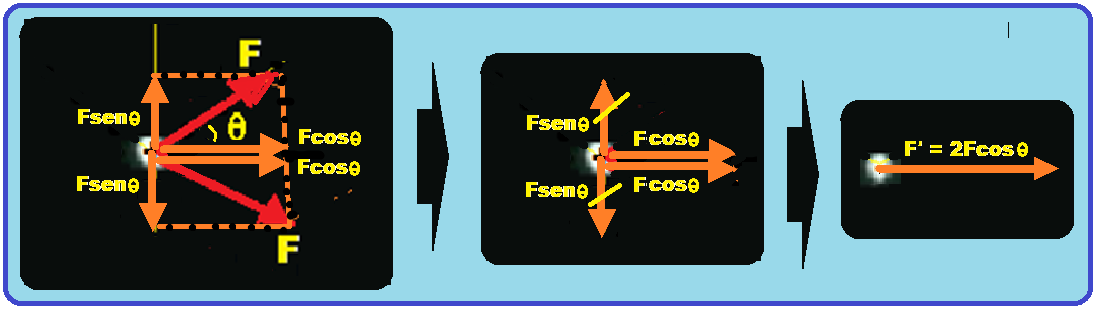
04- Veja nas figuras abaixo que, como é pedido o módulo da força elétrica resultante (F’) em Q3, o sinal de Q3 não influi na resolução já que seu módulo e direção são os mesmos, mudando
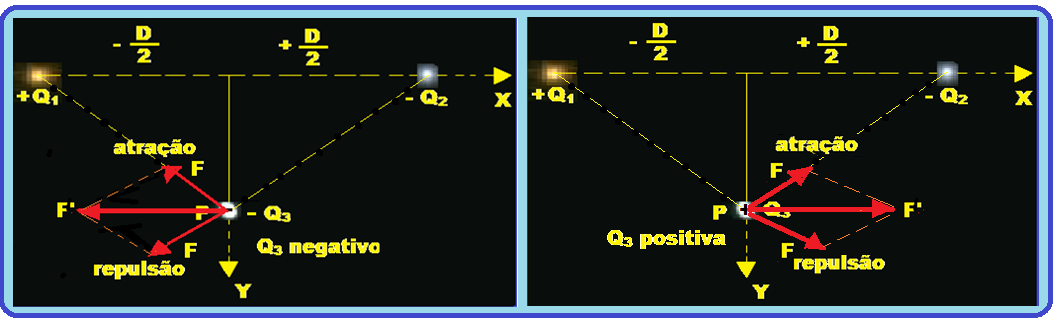
apenas o sentido que depende do sinal de Q3 (leste ou oeste).
Vamos então considerar o caso em que Q3 é positiva e, nessas condições resolver utilizando apenas os módulos (já que os sinais não influem) considerando d = D/2 = 2/2 = 1 m; Q1 = Q2 = Q3
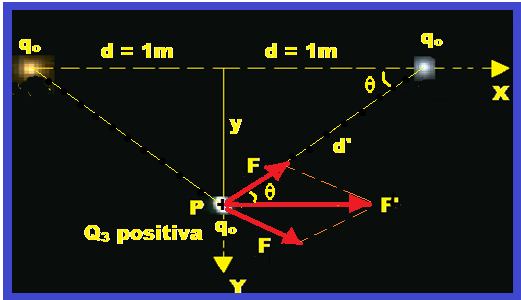
= qo e kqo2 = 10 N.m2.
Cálculo da distância d’ entre as duas cargas qo aplicando Pitágoras no triângulo retângulo na figura acima.
![]()


Decompondo cada F em suas parcelas Fx e Fy, na vertical elas se anulam, pois possuem o mesmo módulo (Fy = Fsen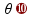 .
.
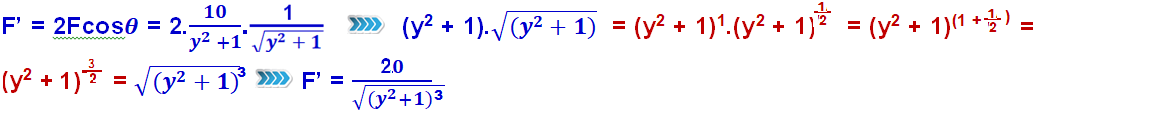
R- B
05-
Força eletromotriz induzida pelo movimento
Força eletromotriz gerada por um condutor móvel num campo elétrico uniforme
Força eletromotriz ε gerada por um condutor móvel imerso num campo elétrico uniforme ![]() esse condutor tem o comportamento de um gerador mecânico de eletricidade de fem ε.
esse condutor tem o comportamento de um gerador mecânico de eletricidade de fem ε.
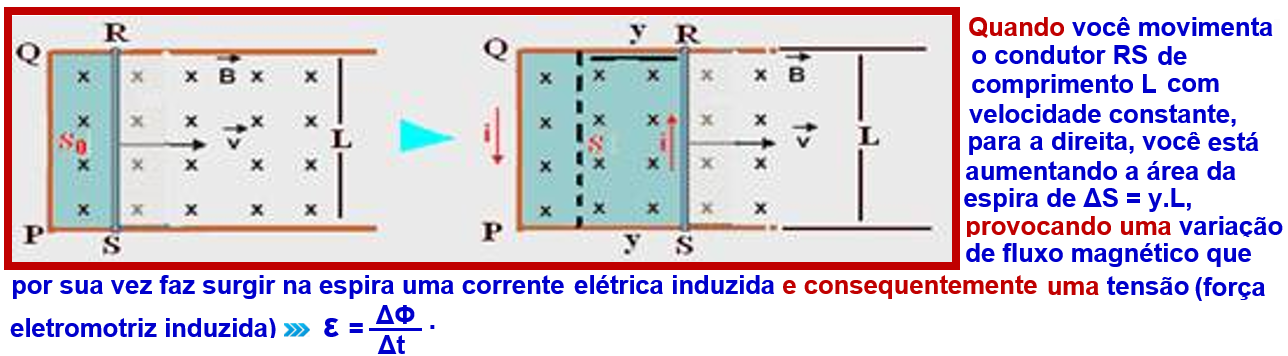

São fornecidos: módulo do campo magnético B = 6,0 T; comprimento da barra condutora L = 1,0 m e velocidade de deslocamento da barra condutora v = 2 m/s.
Cálculo da força eletromotriz induzida (![]() ) na barra condutora pela expressão
) na barra condutora pela expressão  = B.L.v = 6.1.2
= B.L.v = 6.1.2 ![]()
![]() = 12 V.
= 12 V.
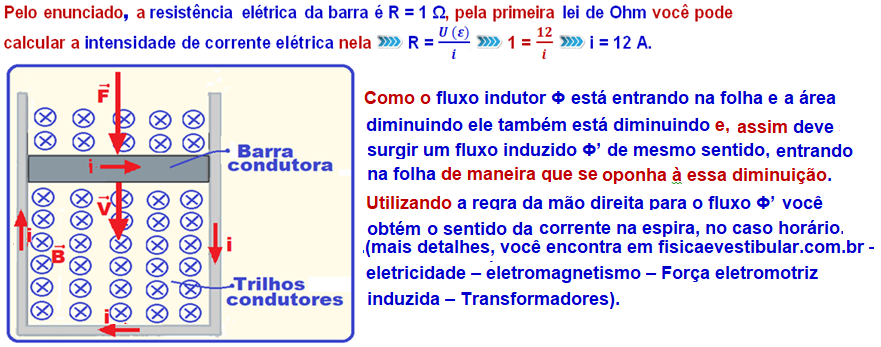
Estando a barra descendo com velocidade constante (equilíbrio dinâmico “força resultante nula”) então deve surgir sobre ela uma força magnética de intensidade Fm (vertical e para cima) que deve anular a força externa de intensidade F (vertical e para baixo).
Essa força magnética tem as seguintes características:

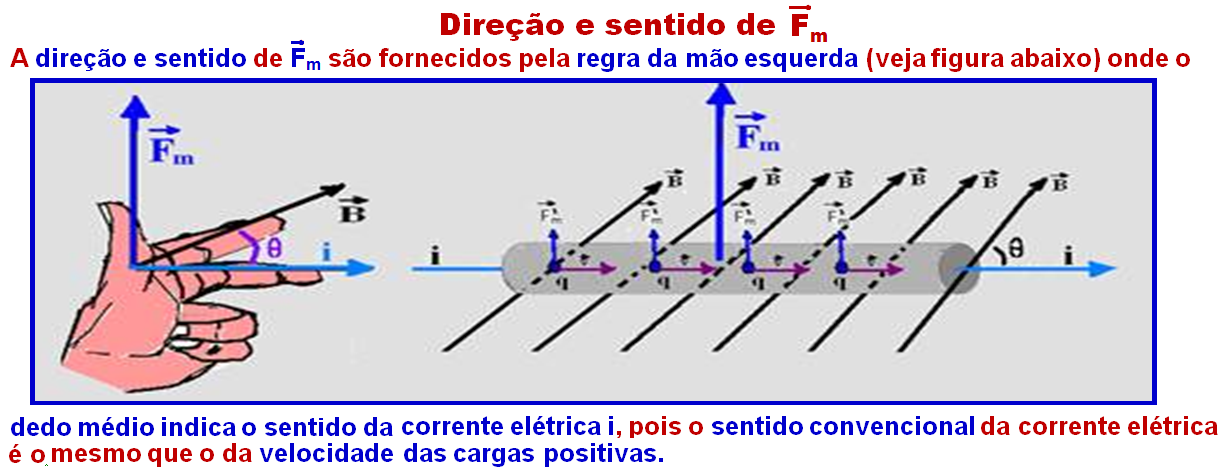
No caso do exercício a força magnética tem direção vertical e sentido para cima (figura abaixo).
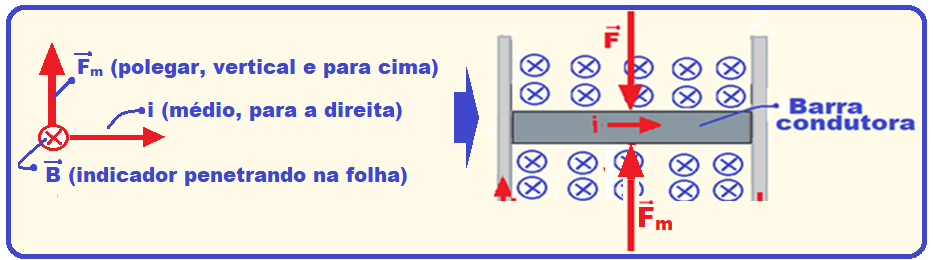
Cálculo da intensidade da força magnética pela expressão Fm = B.i.L.sen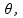 sendo dados: B = 6 T; i = 12 A; L = 1 m e
sendo dados: B = 6 T; i = 12 A; L = 1 m e 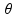 = 90o:
= 90o:
Fm = 6.12.1.1 ![]() Fm = 72 N.
Fm = 72 N.
R – E
06- Trecho AB ![]() trata-se de uma expansão (volume aumentando) isotérmica (ocorre à temperatura T constante TA = TB).
trata-se de uma expansão (volume aumentando) isotérmica (ocorre à temperatura T constante TA = TB).
Trecho BC ![]() trata-se de um aquecimento TC > TB (a isoterma que passa por C está mais afastada da origem que a isoterma que passa por B) isovolumétrico (isocórico ou isométrico) a volume constante.
trata-se de um aquecimento TC > TB (a isoterma que passa por C está mais afastada da origem que a isoterma que passa por B) isovolumétrico (isocórico ou isométrico) a volume constante.
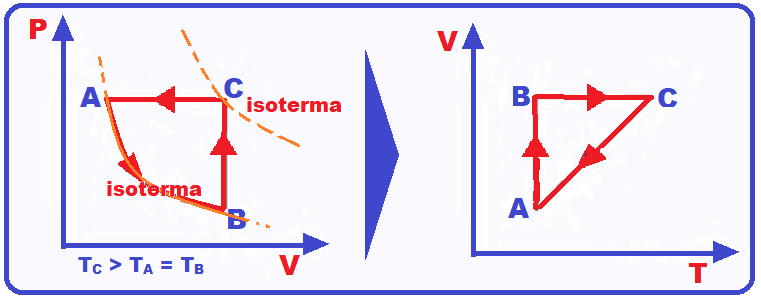
Trecho CA ![]() trata-se de uma compressão (volume diminuindo) junto com um resfriamento TC > TA (a isoterma que passa por C está mais afastada da origem que a isoterma que passa por A) isobárica (pressão constante).
trata-se de uma compressão (volume diminuindo) junto com um resfriamento TC > TA (a isoterma que passa por C está mais afastada da origem que a isoterma que passa por A) isobárica (pressão constante).
R – A
07-

08- Tipicamente o binário de estrelas é um sistema isolado não sujeito à ação de forças externas, mantido exclusivamente pela ação da força de interação gravitacional entre ambos os corpos (lei da Gravitação Universal) .
Expressão matemática da lei da Gravitação Universal
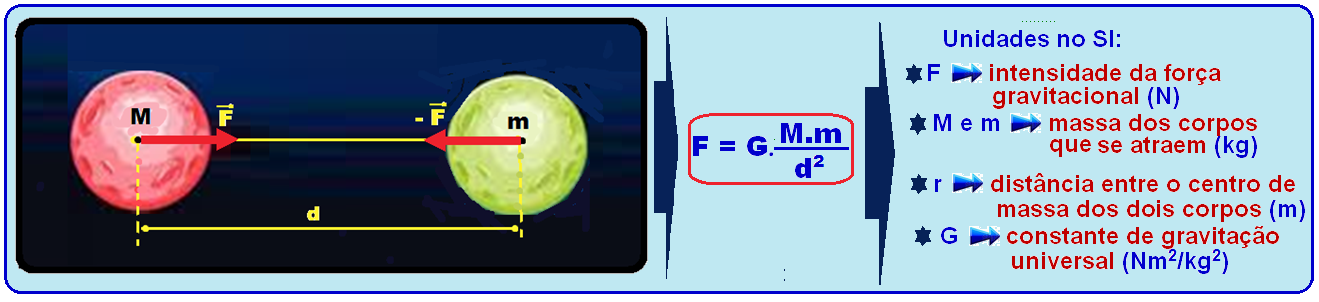
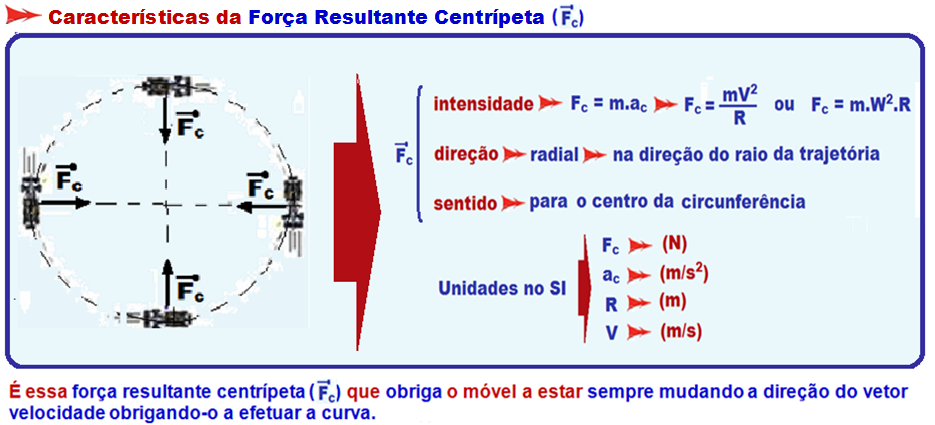

Pelo enunciado o período de rotação (T) é constante o que implica que a velocidade angular (W = 2π/T) também é constante, pois todas as grandezas dessa equação são constantes.

Assim, a energia cinética de cada estrela (e do sistema) também é constante e será conservada o que pode ser provado pela expressão da energia cinética (Ec = M.V2/2), sendo M e V constantes.
R- B
09-

R- B
10- Observe que, quando o enunciado afirma que a potência fornecida nessa transformação foi de P = 360 cal/s, ele está informando que uma fonte está fornecendo Q = 360 calorias em cada segundo durante toda a transformação.

Vamos agora calcular o calor específico no estado líquido já que no estado sólido não é possível, pois o gráfico não fornece a temperatura inicial em que começa a transformação.

R- C
11- A densidade linear da primeira corda (µ1) é maior do que a da segunda (µ2), ou seja, µ1 > µ2.
Quando o pulso chega ao ponto de junção das cordas, ocorre ao mesmo tempo refração e reflexão. Esse ponto (junção) funciona como uma extremidade livre e o pulso refletido retorna sem inversão de fase.
O pulso refratado tem sempre a mesma fase do incidente.
Parte da energia do pulso incidente é transmitida ao pulso refratado e parte ao pulso refletido, diminuindo assim a amplitude desses dois pulsos, ou seja, A > A1 e A > A2.

A força de tração (T) nas duas cordas é a mesma e a velocidade em cada corda é fornecida por
![]()
Observe na expressão acima que a velocidade V é inversamente proporcional à densidade linear µ, assim, a velocidade da onda na corda mais densa “mais pesada” é menor do que a velocidade na corda menos densa “mais leve”. Então, V2 > V1.
A frequência f é a mesma nas duas cordas, pois a fonte é a mesma.
V = λf ![]() f = V/λ
f = V/λ ![]() f = V1/λ1 e f = V2/λ2
f = V1/λ1 e f = V2/λ2 ![]() V1/λ1= V2/λ2 (I)
V1/λ1= V2/λ2 (I)
Observe na expressão (I) que, quanto maior a velocidade V maior o comprimento de onda λ. Portanto o comprimento de onda da corda menos densa é maior que o da corda mais densa.
R – B
12-

Como o amperímetro ideal indica corrente elétrica nula na pilha (gerador) 2, nele, i = 0, ou seja, o gerador está em circuito aberto, portanto você tem a situação da figura baixo:
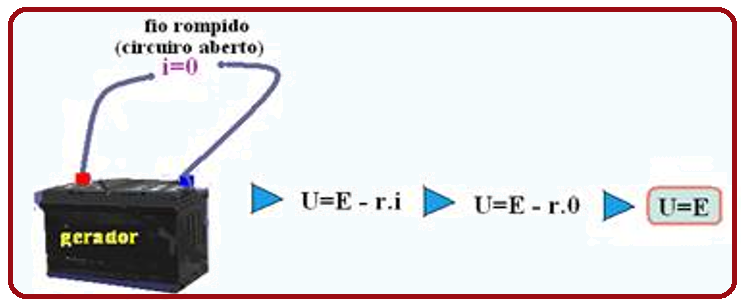

Assim, a tensão (ddp, voltagem “U”) nos terminais da lâmpada de resistência RL será a própria força eletromotriz da pilha 2 ( ), ou seja, U =
), ou seja, U = ![]() .
.
Então o circuito ficará conforme o indicado nas figuras abaixo onde, na sequência, é calculada a resistência equivalente:
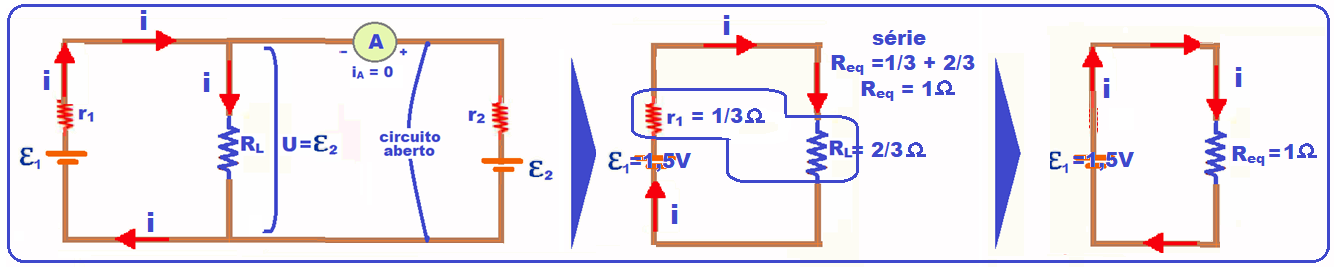 Req = U(
Req = U( )/i
)/i ![]() 1 = 1,5/i
1 = 1,5/i ![]() i = 1,5 A.
i = 1,5 A.
A ddp pedida na lâmpada de resistência RL = 2/3 Ω será ![]() RL = U/i
RL = U/i ![]() 2/3 = UL/1,5
2/3 = UL/1,5 ![]() UL = 3/3
UL = 3/3 ![]() UL= 1 V
UL= 1 V
R- D
