RESPOSTAS
01 – O exercício mesmo nos dá a direção que precisamos seguir, vamos utilizar a fórmula da densidade:
d =
Aonde:
d é a densidade
m é a massa
V é o volume
A massa é dada, porém falta o volume. Temos que modelar a moeda como se fosse um cilindro:
V = área da base X altura (a altura é a espessura e área da base é dada)
Nossa moeda V =
Substituindo na fórmula da densidade:
d =
O exercício fornece o diâmetro, então precisamos substituir o r por D (diâmetro). Sabemos que o diâmetro é metade do raio:
r =
Portanto o raio ao quadrado:
r² =
Temos então a fórmula final da densidade:
d =
O diâmetro é dado em mm passando para cm basta dividir por 10:
D = 2 cm
O mesmo para a altura ou espessura:
h = 0,22
Calculando (podemos deixar as medidas em gramas e cm³, visto que o resultado final está representado nessas medidas):
d =
d = 6,94 g/cm³ (alternativa D)
02 – Esse exercício assusta de primeira, mas vamos com calma. Vamos começar calculando quanto de energia será gerada pela combustão. Essa energia representa o quanto de energia que será consumida para se produzir a energia elétrica desejada. A gasolina libera 3,2.104 kJ/L, temos 5 L de gasolina, portanto:
3,2.104.5 = 16.104 kJ de energia total
Agora que sabemos a energia total e o exercício nos forneceu a energia convertida em elétrica, apenas precisamos calcular a porcentagem, ou seja, o rendimento:
rendimento =
Precisamos calcular a energia liberada. Como 1 kWh = 3,6.10³ kJ, então 8,6 kWh:
3,6.10³.8,6 = 30,96.10³ kJ = 3,096.104 kJ
Substituindo na equação do rendimento:
rendimento =
rendimento =
03 – Nesse exercício precisamos apenas calcular a altura em ambos os casos e comparar:
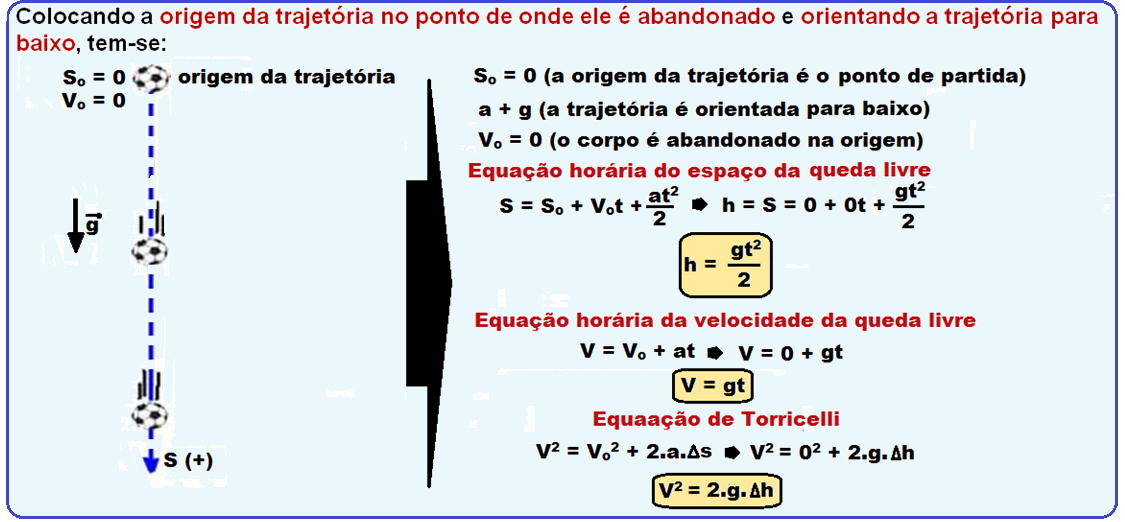
Como explicado acima, o ponto de partida é zero e sua velocidade inicial também. Sendo assim a equação horária é reduzida para:
h =
Aonde:
h é a altura da queda (ou S que seria o deslocamento final)
g é a aceleração da gravidade
t é o tempo da queda
Calculando para a época de estiagem (t = 2 s):
Calculando o outro caso (t = 1,6 s):
h =
h =
Calculando a diferença:
20 – 12,8 = 7,2 m (alternativa B)
04 – É o exercício mais difícil até agora, vamos por partes:
Observando a imagem acima é preciso destacar algumas coisas. Para se manter a caixa parada na rampa é necessário uma força de intensidade igual à
Ou seja a força que o homem deve executar somada com a força de atrito devem ser iguais à
Aonde:
F é a força exercida pelo homem
Fat é a força de atrito
Agora que sabemos dessa relação, podemos calcular a força de atrito no primeiro caso. Observe que o exercício nos forneceu F nesse caso, mas para calcularmos Fat ainda precisamos encontrar PP:
A imagem acima explica como encontrá-lo usando o triângulo retângulo. Esse sen é equivalente ao seno dado no plano. Substituinto na fórmula acima, aonde P é o peso da nossa caixa:
PP = P.sen
PP = 1000.0,6
PP = 600 N
Agora que sabemos PP, podemos calcular a força de atrito:
Fat = PP – F
Fat = 600 – 200
Fat = 400 N
Precisamos desse Fat para calcularmos o coeficiente de atrito da superfície, a fórmula é apresentada abaixo:
Aonde:
Isolando o coeficiente:
Substituindo:
Calculando:
Agora que encontramos o coeficiente de atrito podemos passar para o segundo plano, lembrando que esse coeficiente é o mesmo em ambos os casos visto que o material da rampa é o mesmo. Vamos começar pela força de atrito:
Fat =
Substituindo:
Fat =
Calculando:
Fat =
Sabendo da força de atrito, só nos resta achar Pp:
PP = P.sen
PP = 1000.0,8
PP = 800 N
Agora que sabemos as duas forças:
Isolando F:
F = PP – Fat
Substituindo:
F = 800 – 300
F = 500 N (alternativa E)
05 – Vamos analisar todas as afirmações:
A letra A de cara já é a correta, pois a energia cinética é máxima nos pontos onde a energia potencial é mínima, pois toda essa energia foi justamente transformada em cinética.
A B está errada porque como o ponto N está lozalizado em um ponto mais alto, ele possui uma energia potencial maior, pelo mesmo raciocínio apresentado na justificativa anterior. O mesmo raciocínio explica o motivo da afirmação C estar errada também.
Em D o correto seria a energia cinética é mínima, pois o movimento parte dele.
Em E a energia potencial é mínima, visto que a altura é mínima.
06 – Esse exercício apresenta a relação entre força,área e pressão de uma forma interessante. Vamos aos cálculos:
Como podemos ver pressão é a força exercida em uma determinada área. Sabemos que a área da janela oval é 14 vezes menor que a da membrana timpânica, sendo assim a pressão exercida deve ser 14 vezes maior, por a área e a pressão serem inversamente proporcionais. Agora observe também que a força exercida na janela oval é 1,5 vezes maior, como a força e a pressão são diretamente proporcionais, então temos que a pressão é:
14.1,5 = 21 vezes maior (alternativa D)
07 – Para esse exercício precisamos da fórmula a seguir:
Substituindo na fórmula:
Isolando P´:
Calculando:
Ou seja:
P´ = 120 cm
Para que a imagem seja refletida de forma visível na caixa o espelho deve se encontrar na metada da distância aonde quer se projetar a imagem e sua imagem, portanto o espelho deve ser localizado 60 cm após a placa de madeira. Essa relação se dá justamente por questões de simetria, visto que o espelho reflete exatamente a imagem.
08 – Para conseguirmos resolver exercício precisamos encontrar a equação que é responsável por esse gráfico. Precisamos de uma relação que expresse P em função de U:
Como podemos perceber a potência é proporcional ao quadrado do diferencial, sendo assim o gráfico deve ser uma parábola, excluímos as alternativas B, D e E. Como é uma relação diretamente proporcional, então quanto maior o P, maior o U. Sendo asssim a alternativa correta é a C.
09 – Apenas precisamos calcular os dois casos e compará-los.
Isolando o tempo:
Substituindo:
Calculando:
Calculando a diferença de tempo:
Transformando em min (multiplicando por 60):
4,2 min = 4 min 12 segundos (alternativa E)
10 – Para encontrarmos a velocidade angular primeiro precisamos encontrar o número de rotações por segundo (frequência). Como temos rotações por minuto, basta então dividir por 60:
f =
Como cada volta tem o valor de 2
5. 2
Como
10
Abaixo segue uma relação entre velocidade angular e escalar:
Observe que para obtermos a velocidade escalar a partir de
Multiplicando a velocidade angular por r:
V = 30.1,2 = 36 m/s (velocidade escalar)
Para encontrarmos a potência total, aquela que o vento exerce na pá para que ela gire gerando energia elétrica, precisamos da relação abaixo. Essa potência é importante para encontrarmos a quantidade de energia cinética que o vento exerce na pá:
Aonde:
Pu é a potência gerada
Pt é a potência utilizada para gerar Pu
Isolando Pt:
Pt =
Substituindo:
Pt =
Calculando:
Pt = 2500 W
Ou seja, foram necessários 2500 W de potência originada pelo fluxo do vento para gerar 1500 W de potência elétrica. Agora que sabemos a potência precisamos encontrar a energia cinética, para isso:
Aonde:
P é a potência
W é o trabalho, também pode ser usado E de energia
Utilizando energia ao invés de trabalho e isolado-a:
E = P.
Substituindo:
E = 2500.
Calculando:
E = 150000 J = 1,5.105 J (Energia cinética originada do vento)
11 – Para calcularmos a temperatura final precisamos primeiro do volume final. Podemos calcular visto que sabemos que o o êmbolo se deslocou 10 cm:
Volume inicial = 6.10-3 m³
Volume final = Volume inical +
Passando 10 cm para metros (dividir por 100):
10 cm = 0,1 m
Calculando o
Substituindo:
Calculando:
Agora calculando o volume final:
Volume final = 6.10-3 + 2.10-3
Volume final = 8.10-3 m³
Sabendo o volume final podemos utilizar a fórmula a seguir, já que se trata de um gás ideal:
Aonde:
Pi e Pf é a pressão inicial e final
Vi e Vf é o volume inicial e final
Ti e Tf é a temperatura inicial e final
Como é uma expansão isobárica (pressão constante) podemos cortar a pressão em ambos os lados, restando apenas:
Substituindo:
Isolando a temperatura final:
Tf =
Calculando:
Tf = 400 K (temperatura final)
Achamos a temperatura, agora vamos para a segunda parte do exercício. Para calcularmos a quantidade de calor vamos utilizar a primeira lei da termodinâmica. Como se trata de uma transformação isobárica:
Como a pressão é constante o nosso trabalho só depende da variação do volume:
W = P.
Substituindo. Nós calculamos a variação anteriormente (2.10-3):
W = 2.105. 2.10-3
Calculando:
W = 4.102 J
O exercício já nos forneceu a variação de energia interna (600 J). Vamos então substituir na equação da primeira lei:
Isolando a quantidade de calor:
Q =
Substituindo:
Q = 600 + 400
Calculando:
Q = 1000 J (quantidade de calor)
12 – Esse exercício assusta, mas na verdade ele é mais fácil que parece, vamos aos poucos. Primeiramente ele pergunta a intensidade média, que não é nada mais que a quantidade de carga transferida em determinado tempo:
Substituindo. Lembre-se que o tempo está em ms = 1.10-3 s, portanto 200 ms = 0,2 s:
i =
Calculando:
i = 150 A (intensidade média)
Já calculamos a intensidade média. Agora vamos para a segunda parte do exercício. Precisamos primeiramente calcular quanto de energia será fornecido por esse raio (Energia total):
Ou seja:
W = Q.U ou E = Q.U (No caso o trabalho é a variação de energia, como a energia se mantém constante durante o raio então W = E)
Substituindo:
E = 30.1,8.108
E = 54.108 J
Agora que sabemos a energia total precisamos calcular a energia de cada bateria, vamos utilizar o mesmo procedimento. A bateria tem uma carga de 50 A.h, como 1 hora = 3600 s:
QBateria = 50.3600 = 180000 J (carga total da bateria)
Sabendo a carga, podemos substituir na equação:
EBateria = QBateria.UBateria
EBateria = 1,8.105.10
Calculando:
EBateria = 1,8.106 J (energia total de cada bateria)
Como sabemos a energia total e a de cada bateria, basta dividir uma pela outra e encontrar o número de baterias possíveis: