Resolução comentada das questões de FÍSICA da Universidade Estadual Feira de Santana (UEFS-BA-017)
Resolução comentada das questões de FÍSICA da
Universidade Estadual Feira de Santana (UEFS-BA-017)
01-
Colocando as forças que agem em cada bloco apenas na direção do movimento:
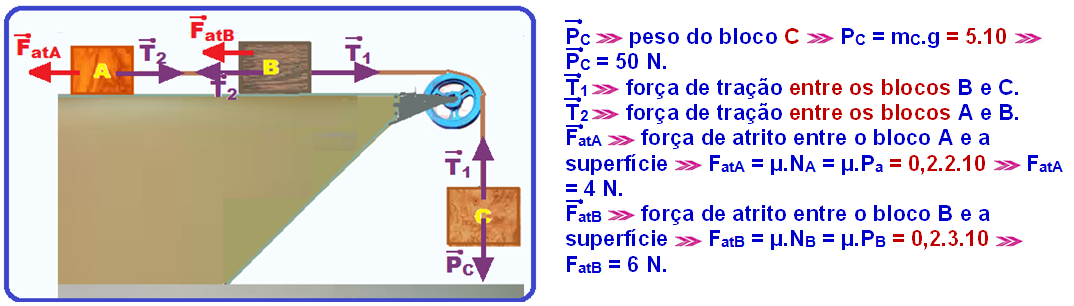
Aplicando a lei fundamental da Dinâmica para cada bloco:
C 
FRC = mC.a PC – T1 = 5.a 50 – T1 = 5.a T1 = 50 – 5a (I).
B FRB = mB.a T1 – T2 – FatB = 3.a T1 – T2 – 6 = 3.a T1 – T2 = 3.a + 6 (II)
A FRA = mA.a T2 – FatA = 2.a T2 – 4 = 2.a T2 = 2.a + 4 (III)
Somando simultaneamente (I), (II) e (III):
(IV) em (I) 30 = 50 – 5a a = 4 m/s2 (V) (aceleração de cada bloco).
(V) em (III) T2 = 2.4 + 4 T2 = 12 N.
R- 04
02- Quando a mola de constante elástica k = 4 N/cm = 400 N/m é comprimida de x = 12cm = 0,12 m (ponto A) ela só possui armazenada energia potencial elástica (Epe = k.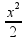
) pois, como V = 0 a energia cinética é nula (Ec = 0) e como a altura não varia a energia potencial gravitacional também é nula (Epg = 0).
A energia mecânica total em A, EmA é apenas a energia potencial elástica EmA = Epe = k.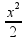 = 400.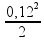
EmA = 200.0,0144 EmA = 2,88 J.
Depois que o bloco é liberado no ponto A ele se desloca até atingir o ponto B onde para (V = 0) na altura H.
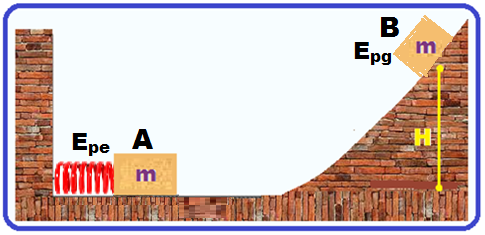
Em B, onde a altura H é máxima, suas energias potencial elástica e cinética são nulas, sobrando apenas a energia potencial gravitacional (Epg = m.g.H) que é a mecânica em B.
EmB = Epg = m.g.H = 1,2.10.H = 12H.
Sendo as forças dissipativas desprezadas, a energia mecânica se conserva EmA = EmB 2,88 = 12H H =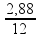 
H = 0,24 m = 24 cm.
R- 01
03-
04-
Expressão matemática da dilatção linear de um sólido
Sendo:
ΔL 
dilatação linear (de quanto dilatou o comprimento ou uma dimensão)
α coeficiente de dilatação linear médio, característica do material que constitui a barra.
Lo comprimento inicial
L comprimento final
Δt intervalo de temperatura
São dados Lo = 20,5 m 
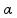= 1,7.10-5/oC Δt = (40 – 20) = 20 oC.
∆L = Lo.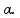
Δt ∆L = 20,5.1,7.10-5.20 ∆L = 697.10-5 m = 6,97.10-3 m ∆L = 6,97 mm
R- 02
05- A troca de calor é entre o calorímetro de capacidade térmica C = 300 ca/oC com temperatura inicial de to =20 oC, a massa ma = 200 g de água de calor específico ca = 1 cal/goC com temperatura inicial to = 20 oC e o bloco de massa mb = 1000 g, calor específico cb = 0,25 cal/goC e temperatura inicial tob = 50 oC.
Após as trocas de calor entre eles todos terão a mesma temperatura t (temperatura de equilíbrio térmico).
A soma das quantidades de calor que eles trocam entre si deve ser nula.
C.(t – to) + ma.ca.(t – to) + mb.cb.(t – to) = 0 300.(t – 20) + 200.1.(t – 20) + 1000.0,25.(t – 50) = 0 300t – 6000 + 200t – 4000 +250t – 12500 = 0 750t = 22500 t = 
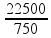
t = 30 oC.
R- 03
06-
Lei de Snell-Descartes
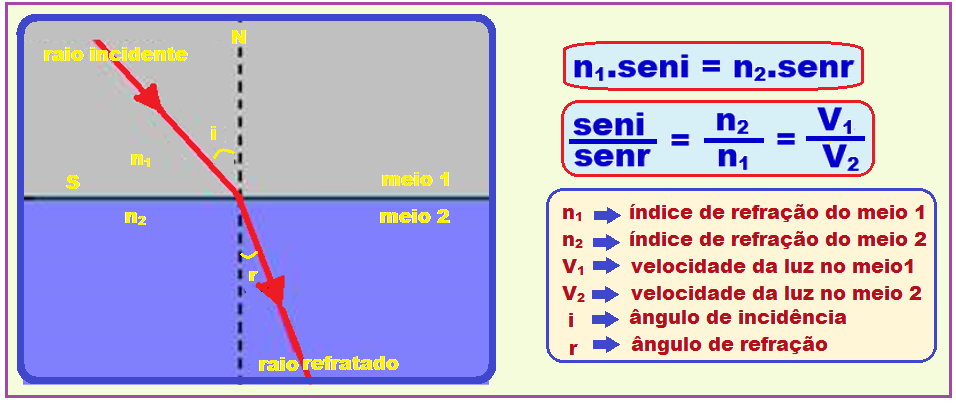
nar.sen
= n.sen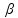
1.0,5 = n.0,87 n = 
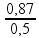
n = 1,74.
R- 04
07-
Expressão matemática do empuxo quando imerso num líquido
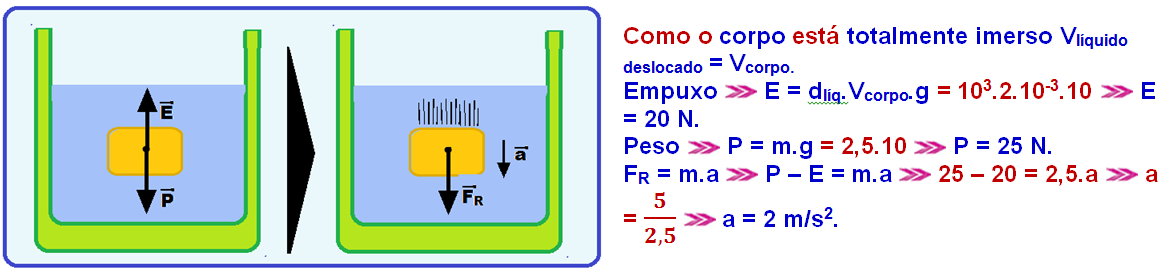
R – 01
08-
IMÃS E CAMPO MAGNÉTICO
IMÃS
Desde a antiguidade se conhecia um mineral, hoje denominado magnetita, composto basicamente por óxido de ferro (Fe3O4) que possuía propriedade de atrair alguns minerais como o ferro, o níquel
e o cobalto e pedras de óxidos de ferro e que são denominadas de imãs naturais.
Essa propriedade recebe o nome de magnetismo e as regiões do imã onde as propriedades magnéticas são mais intensas são denominadas de polos do imã.
R- 05