Resolução comentada das questões de Física da UFRGS – 2017
Resolução comentada das questões de Física da
UFRGS – 2017
01 – Para esse exercício precisamos perceber que a aceleração é única e constante (aceleração da gravidade), já podemos eliminar algumas opções, como essa pedra é arremessada para cima, ela vai perder velocidade, para isso precisamos de uma aceleração negativa, ou seja, a alternativa correta é a C.
02 – Vamos analisar as afirmações individualmente. Começando pela primeira, podemos calcular a velocidade média por:
V =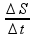 
Aonde:
V é a velocidade média
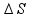é o deslocamento
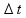é o tempo
Substituindo na equação:
V =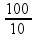
V = 10 m/s
Observe que o resultado do exercício está em Km/h, vamos transformar então, basta multiplicar por 3,6:
V =36 km/h (afirmação I verdadeira)
Para analisarmos a segunda alternativa, podemos calcular a aceleração por:
Aonde:
S é a posição inicial
So é a posição final
Vo é a velocidade inicial
t é o tempo
a é a aceleração
Substituindo:
A terceira afirmação a gente nem precisa calcular, basta pensarmos que se a média da velocidade é de 10 m/s e como não há um deslocamento negativo nesse exercício, então não há maneira da sua maior velocidade ser igual à sua média, portanto afirmação III falsa. Portanto alternativa A é a correta.
03 – Para calcular a massa do exercício, precisamos antes calcular a aceleração que esse corpo sofreu, podemos utilizar nesse caso:
a =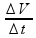
Aonde:
a é a aceleração
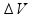é a variação de velocidade
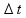é a variação do tempo
Substituindo:
Agora que calculamos a aceleração, só precisamos substituir na equação da força:
F =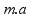 
Aonde:
F é a força exercida
m é a massa
a é a aceleração
Isolando a massa:
V =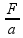 
Substituindo:
V =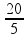
V =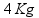 
(alternativa B)
04 – Esse exercício é apenas substituição nas fórmulas corretas. Para a velocidade angular:
W =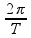 
Aonde:
W é a velocidade angular
T é o período (tempo para uma volta completa)
Substituindo:
W =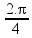 
W =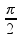 
Já para a aceleração centrípeta:
AC =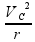
Aonde:
AC é a aceleração centrípeta
VC é a velocidade centrípeta
r é o raio do movimento
Antes precisamos calcular a velocidade centrípeta, observe a imagem abaixo:
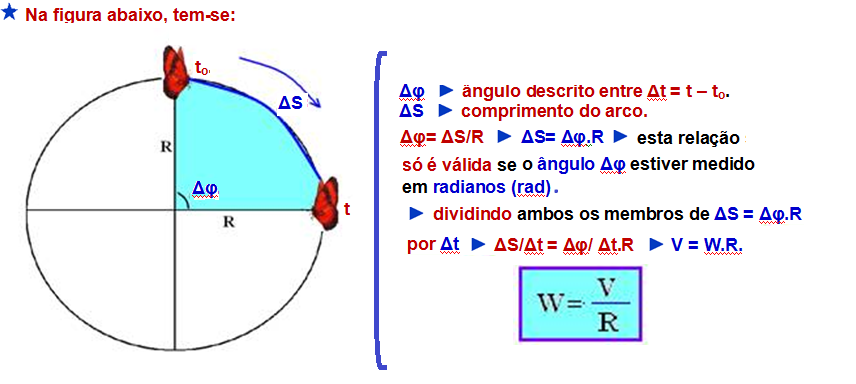
Nela podemos concluir que para passar de uma velocidade angular para centrípeta, nós apenas precisamos multiplicar pelo raio, ou seja:
= 
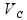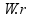
Substituindo a velocidade centrípeta:
Cortando o raio e substituindo pelos valores:
=
= 
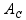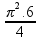
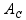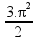(Alternativa correta B)
05 – Para estudarmos esse exercício primeiramente observe a figura a seguir:
Essas são as forças de atração em P exercida por ambos os planetas, como dito no enunciado em P ambas possuem a mesma intensidade, sendo assim podemos igualar suas equações, para esse caso vamos utilizar a lei da gravitação universal:
F =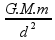 
Aonde:
F é a força gravitacional
G é a constante de gravitação (6,7.10-11 N.m²/Kg²)
M e m são as massas dos corpos sofrendo essa força
d é a distância entre esses corpos
Vamos transformar essa equação para utilizar em nosso exercício:
= 
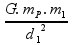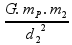
Agora que já igualamos e também adicionamos a massa no ponto P (mP) e dos planetas 1 e 2 (m1 e m2) o mesmo para as distâncias, precisamos substituir seus valores, lembrando que a distância 1 e 2 são diferentes. Podemos também simplificar essa equação cortando o G e o mP, pois eles estão presentes em ambos os lados:
Nessa equação podemos fazer essa troca de m2 com o D/3:
Simplificando:
= 
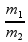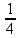
Alternativa A.
06 – Vamos analisar o movimento:
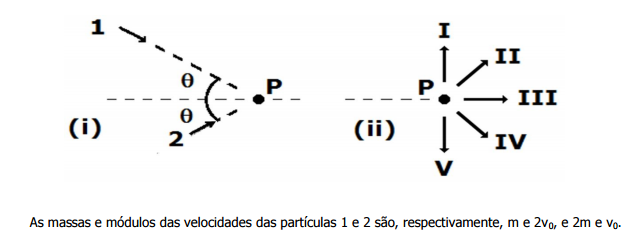
Como podemos perceber o ângulo entre as duas partículas é o mesmo, mas só essa informação não ajuda a desenvolver o problema. Também sabemos que o choque é inelástico, portanto ambas as partículas terminarão o movimento unidas e na mesma direção. Agora vamos analisar a quantidade de movimento em ambas as partículas:
Q =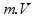 
Aonde:
Q é a quantidade de movimento
m é a massa da partícula
V é a velocidade
Para as duas partículas:
= 
= 
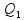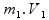
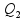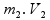
Precisamos estudar o ângulo dessa velocidade:
Ambos V1 e V2 são catetos adjacentes do ângulo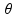 
, sendo assim podemos escrever: (VX é a velocidade no eixo X)
=
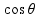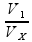
Isolando V1:
= 
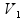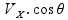
O mesmo acontece para V2 quando analisamos em relação ao eixo X:
=
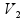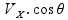
O V0 é a velocidade analisada no eixo X e Y. Para a análise apenas em X podemos fazer o que foi feito abaixo.
Substituindo:
Portanto:
=
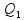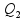
Bom, agora que sabemos que os ângulos e as quantidades de movimento são iguais e o choque é inelástico, resolver esse caso fica muito mais fácil, podemos considerar apenas que a trajetória final é uma “média” das anteriores, ou seja a III, que se encontra na bissetriz do ângulo do movimento. Alternativa C.
Direção do movimento
Observação:
(Nesse caso eu não analisei em Y, porque queria mostrar essa característica do movimento, já que o choque é inelástico, suas massas são iguais e sua velocidade em X é a mesma, podemos considerar o movimento final como a bissetriz do ângulo, já que se fizermos os cálculos em Y, teremos que a velocidade de 1 em Y é igual a velocidade de 2, porém negativa, substituindo na quantidade de movimento elas se anularão, resultando em QY=0. Por esse motivo o movimento final só se desenvolve em X.)
07 – Bom, nesse exercício não tem jeito, precisamos resolver a equação envolvendo o movimento. Como sabemos em um choque inelástico as duas partículas ficam juntas após o choque e sua massa é somada, essa informação é muito importante para resolvermos esse exercício. A quantidade de movimento antes do choque deve ser igual a depois do choque, portanto:
Vamos agora substituir pelas fórmulas:
Como sabemos que a massa final (m3) é a soma das outras duas massas (m+2m=3m):
= 
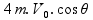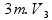
Isolando a velocidade final (V3) já cortando a massa:
=
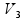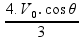
Alternativa E.
08 – Assim como no caso do espaço em S = ΔV . Δt podemos usar o cálculo de área para esse exercício, pois o trabalho pode ser escrito como:
W = F.d
Aonde:
W é o trabalho
F é a força exercida
d é a distância do deslocamento
Calculando a área do triângulo:
A =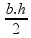 
A =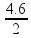
A =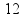
Como o trabalho é igual à área temos um trabalho de 12 J. Alternativa B.
09 – Para esse exercício precisamos usar o mesmo raciocínio da área utilizado acima para achar o trabalho. Feito isso a gente só precisa usar a afirmação de que “o trabalho das resultantes que agem sobre um corpo é igual à variação de energia cinética sofrida pelo corpo” para igualar trabalho e energia cinética, chegando no resultado. Vamos as contas:
Igualando com o trabalho temos 6 para x=2 e 12 para x=4. Alternativa E.
10 – Para esse exercício não precisamos de fórmulas, basta apenas pensarmos um pouquinho nas condições. Temos um fluído se deslocando por um tubo, a quantidade de água que passa se mantém constante, para que a mesma quantidade de água passe por trecho menores, precisamos que algo aconteça, senão esse tubo irá explodir. Dessa forma para passarmos a mesma quantidade de água em uma parte menor na mesma quantidade de tempo, ela precisa passar mais rapidamente, logo quanto menor a seção, maior a velocidade que a água deve passar.
No nosso exercício a área é quatro vezes menor, portanto a velocidade do fluído deve ser 4 vezes maior. Alternativa A. Segue abaixo uma explicação com fórmulas sobre o assunto.
11 – Vamos analisar as afirmações individualmente. A afirmação I de cara é falsa, pois alguns materiais apresentam coeficiente de dilatação negativo, ou seja, quando são aquecidos eles diminuem de tamanho, ao invés de aumentar, um exemplo disso é a água que em sua forma sólida ocupa um volume maior que em sua forma líquida.
A afirmação II é de fato verdadeira, não só a temperatura como o volume da água varia com a pressão do ambiente. Basta lembrarmos dos diagramas de fases (gráficos p x T).
A afirmação III está correta, quando qualquer substância está mudando da fase ela permanece em temperatura constante até o final da transformação, ou seja, até a quantidade de calor ser suficiente para transformar toda essa substância. Nesse ponto temos o que chamamos de calor latente, como estamos estudando um processo de ebulição, temos o calor latente de vaporização.
Alternativa D é a correta.
12 – Nesse caso temos a temperatura constante (transformação isotérmica), sendo o gráfico correto apresentado na imagem a seguir:
Os outros gráficos podem ser eliminados por exclusão, não temos uma pressão ou volume igual ou menor que zero (podemos eliminar C e D), sabemos também que com temperatura constante e volume variando a pressão não pode ser constante eliminando a alternativa E e, finalmente, quanto maior a pressão, menor o volume, pois a substância é muito mais comprimida, eliminando a B. Alternativa correta A.
13 – Vamos analisar as afirmações. Começando pela primeira, a sublimação (passagem do estado sólido para o gasoso ou vice-versa) realmente não pode ocorrer em pressões maiores que Pa ou até temperaturas maiores que Ta, pois, observando o gráfico, a partir desses pontos não há mais um estágio em que a substância passe do estado gasoso (G) para o sólido (L) sem passar pelo estado líquido (L), ou seja, não há uma linha de transição de estado físico de G para L.
A afirmação II parece ser muito difícil, mas vamos com calma. Uma transformação isotérmica (temperatura constante) se dá pela alteração da pressão e volume, nesse caso ao mantermos a temperatura em b constante, podemos alterar a pressão fazendo com que a substância (ponto b) vá para um ponto mais baixo do gráfico, observe abaixo:
Observe que ao diminuirmos a pressão a substância pode passar para o estado gasoso (G), ocorrendo a vaporização. Podemos perceber também que quando realizamos uma transformação isobárica (pressão constante) por um processo semelhante ao anterior, mas deslocando a temperatura dessa vez:
Ocorre também a vaporização, pois a substância se deslocou, também, até o estado gasoso (G), ou seja, afirmação II verdadeira.
No caso de c para d, a pressão é constante (isobárica) ocorrendo a passagem do estado líquido para o sólido (solidificação), afirmação III verdadeira. Sendo assim, alternativa E correta.
14 – Como sabemos da primeira lei a variação da energia interna só depende da temperatura ou dos pontos finais e iniciais de um gráfico P x V, como nesse caso ambos os pontos iniciais e finais dos dois processos possuem mesma posição, então a variação de energia em ambos os processos é a mesma. O trabalho pode ser calculado pela área encontrada embaixo da curva, vamos analisar as curvas:
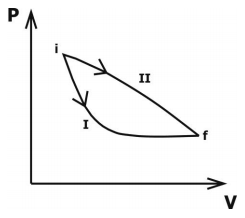
Observe que a área abaixo do processo I é muito menor que a do processo II, sendo assim o trabalho é menor, consequentemente, alternativa B.
15 – Esse exercício parece muito difícil, mas na verdade ele não é tanto, vamos com calma. A primeira afirmação não é verdadeira, pois, vamos analisar a figura:
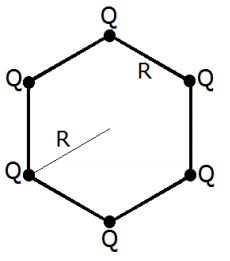
O campo resultante é a somatória de todos os campos, nesse caso temos 6 campos distintos, mas com intensidades iguais, pois a carga em todos eles é a mesma, sabendo disso e analisando as disposições das cargas podemos concluir que para cada carga há uma carga igual no canto oposto, gerando um campo de mesma intensidade, mas de sentido oposto, ou seja, se anulando entre si, observe abaixo:
Observe que esse fenômeno acontece para todos os campos, sendo assim o campo elétrico resultante exatamente no centro da figura é nulo. Afirmação I falsa.
Podemos fazer essa mesma análise para a alternativa III, ou pensarmos que como não há um campo elétrico no ponto, também não é possível haver uma força elétrica resultante. Alternativa III falsa.
(Para a alternativa II eu não consegui explicar o exercício de uma forma que não utilizasse integrais.)
16 – Para esse exercício precisamos considerar a fórmula da potência:
P = i.U
Aonde:
P é a potência
i é a intensidade da corrente
U é a tensão do sistema (ddp)
Nesse exercício, para se ter a potência total, precisamos da corrente total e da tensão total, que o exercício já nos fornece (V).
A intensidade total pode ser calculada por:
i =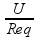 
Aonde:
i é a intensidade de corrente
U é a tensão (ddp)
Req é a resistência equivalente (Resistência total no circuito)
Podemos substituir essa equação na equação da potência, obtendo:
P =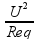 
Bom, já sabemos o valor da tensão, então só nos resta encontrar o valor de Req. Podemos perceber que temos 3 ligações em paralelo, duas com o valor 2R (esse valor vem pelo fato de que nas ligações de cima e de baixo temos R e R em série, ou seja, R + R = 2R) e uma com valor R, primeiramente vamos somar as duas com valor 2R:
Sendo R1 a soma da resistência em ambos.
Somando:
= 
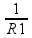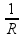
Então temos que R1 = R, agora precisamos fazer essa mesma operação para o resistor do meio, porém, observe que quando somamos dois resistores em paralelo com a mesma resistência, o resultado é a metade deles. Isso é uma regra geral que pode ser aplicada, então ao somar R1 com o resistor do meio temos que Req =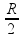 
.
Substituindo na equação da potência, lembrando que a tensão é V:
P =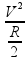 
P =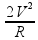 
(alternativa A)
18 – Para esse exercício precisaremos apenas utilizar a Lei de Lenz:
Com as explicações acima podemos perceber que em 1 (polo norte se aproximando) temos uma corrente induzida no sentido horário e, em 2 (polo norte se afastando), temos uma corrente induzida no sentido anti-horário. Alternativa C.
OBS: Uma forma fácil de se entender a Lei de Lenz é pensar que ela deve se opor a corrente gerada pelo campo magnético, ou seja, com o polo norte se aproximando de 1, pela regra da mão direita, a corrente deve ter sentido anti-horário, logo a corrente induzida deve ser no sentido horário. O mesmo ocorre para 2, mas em sentidos opostos.
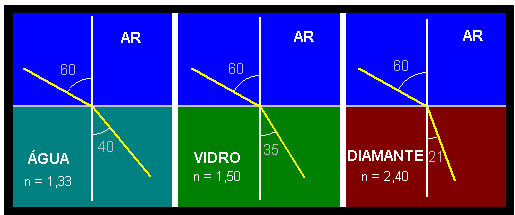
20 – Quando a luz passa de um meio para outro e ocorre a refração precisamos ter em mente que, independente dos meios, a frequência sempre será constante (sobra apenas a alternativa C e D). Agora precisamos apenas analisar a velocidade de propagação, que é menor quanto mais refringente o meio, observe abaixo.
Como podemos perceber na imagem abaixo, quanto mais refringente o meio, menor o ângulo entre o feixe de luz e a reta normal.
Em n2 o ângulo é menor que em n1, logo n2 é mais refringente, sendo assim a velocidade de propagação da luz no meio é menor.
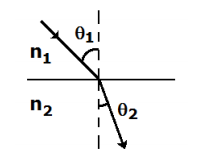
Alternativa D.
21 – Começando pelos mais simples, esse fenômeno não pode ser de refração (não há uma troca de ambiente) e reflexão (a luz do laser até pode sofrer um pouco de reflexão do fio do cabelo, mas ela é mínima e não vai de encontro ao anteparo).
A polarização ocorre com a propagação dos feixes de luz em apenas um plano, nesse caso a luz no anteparo seria apenas uma linha reta, sem as partes escuras, o que não acontece na imagem.
Se houvesse dispersão da luz, não haveria um padrão como podemos observar no anteparo.
Restando apenas a alternativa A, que é correta justamente pelos fenômenos de difração apresentaram esse mesmo padrão.
22 – Como sabemos, a frequência é o inverso do período, ou seja, quanto maior a frequência, menor o período. Sendo assim o diapasão 1 tem o maior período.
Como as ondas estão no mesmo meio, então sua velocidade de propagação não muda, o que muda são suas frequências e o comprimento de onda. Quanto menor a frequência, mais grave é o som emitido, ou seja, o diapasão 3 tem o som mais agudo.
23 – Esse exercício parece mais difícil do que ele realmente é, mas podemos fazer ele de forma bem intuitiva. Observe que a cada 5730 anos a quantidade em ppb na amostra se reduz pela metade. Observe também que 10/16 = 0,625, ou seja, a amostra se reduziu pela metade 4 vezes, como mostrado abaixo:
n2 = 16
n = 4 (desconsideramos a parte negativa, pois não existe tempo negativo)
ou
10/2 = 5; 5/2 = 2,5; 2,5/2 = 1,25; 1.25/2 = 0,625; (dividido por dois um total de 4 vezes)
Como a amostra se reduziu pela metade 4 vezes, temos então 4.5730 = 22920 anos. Alternativa E.
24 – Para esse exercício precisamos relembrar das fórmulas do efeito fotoelétrico:
Sabemos que a velocidade de onda pode ser escrita como:
V =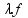 
Aonde:
V é a velocidade de propagação da onda
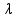é o comprimento de onda
f é a frequência
Isolando a frequência: (como estamos trabalhando com fótons, então a velocidade de propagação é a velocidade da luz = c)
f =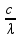 
Substituindo pelos valores:
f =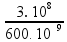 
= 
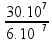
Calculando:
f =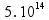 
Hz (resta apenas as alternativas D e E)
Para a energia:
Substituindo na equação:
W =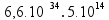 
Calculando:
W =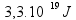 
(alternativa E)
25 – Vamos analisar as afirmações individualmente. Para responder a afirmação I precisamos apenas observar o gráfico, observe que para qualquer f que pegarmos após fII nós temos uma energia maior em fI. Observe abaixo:
Afirmação I está incorreta.
Agora para a segunda afirmação:
Vamos isolar a energia cinética:
Observe que para a energia cinética ser maior o Wmin deve ser o menor possível, ou seja, na placa II como ela tem uma energia cinética menor, podemos concluir que o trabalho realizado para retirar os elétrons é maior que em I. Afirmação II correta.
Para a terceira afirmação:
Isolando o h:
h =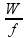 
Podemos perceber a relação entre W, f e a constante h. Afirmação III correta.
Sendo assim, a alternativa D é a correta.