Resolução comentada das questões de Física (ECONOMIA) da Fundação Getúlio Vargas (FGV-SP) 2017
Resolução comentada das questões de Física (ECONOMIA) da
Fundação Getúlio Vargas (FGV-SP) 2017
01- As alternativas (A) e (B) estão erradas, pois o gráfico Sxt fornece apenas a posição do móvel em cada instante, independente da trajetória do mesmo. 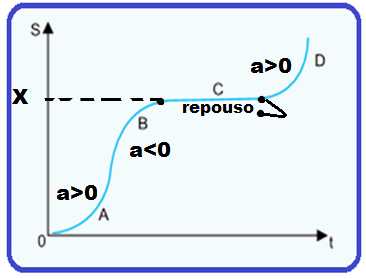
Pelo enunciado o trecho C não é arco de parábola (reta) o que significa que nesse trecho o móvel está em repouso numa posição qualquer, por exemplo X.
Nos trechos A, B e D o movimento é um MUV de equação S = So + Vot + 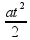 onde a é a aceleração que é positiva com a concavidade da parábola para cima e negativa com a concavidade para baixo.
onde a é a aceleração que é positiva com a concavidade da parábola para cima e negativa com a concavidade para baixo.
R- D
02-
Dilatação do tempo
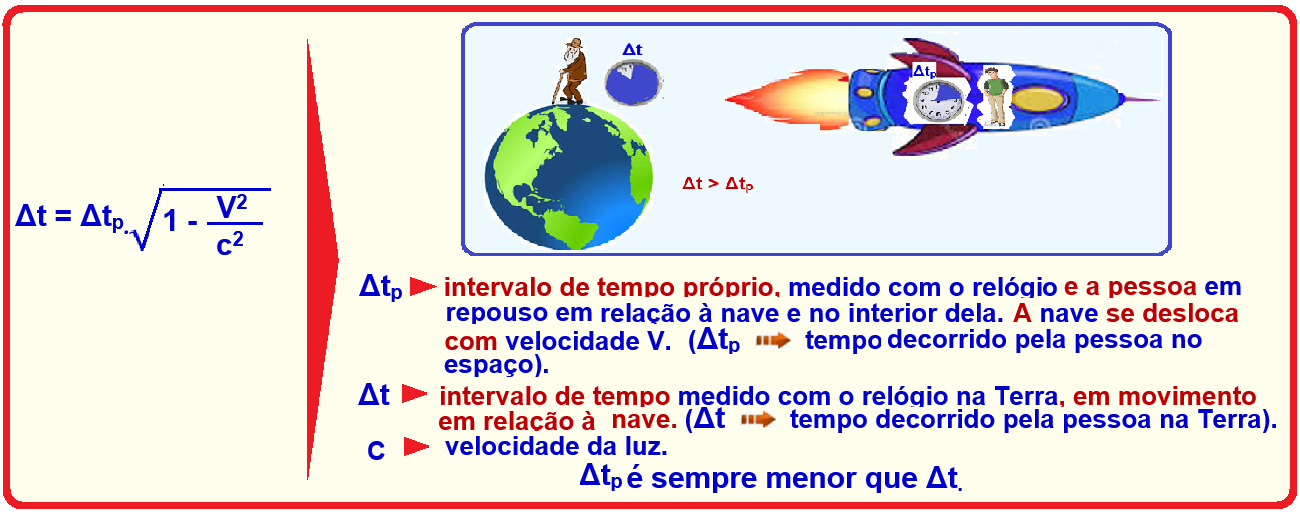

R- B
03- 
R- A
04- Como não houve interferências passivas e, durante o salto apenas a força peso ( força conservativa) realiza trabalho, você pode aplicar o princípio da conservação da energia mecânica, colocando o referencial no solo:
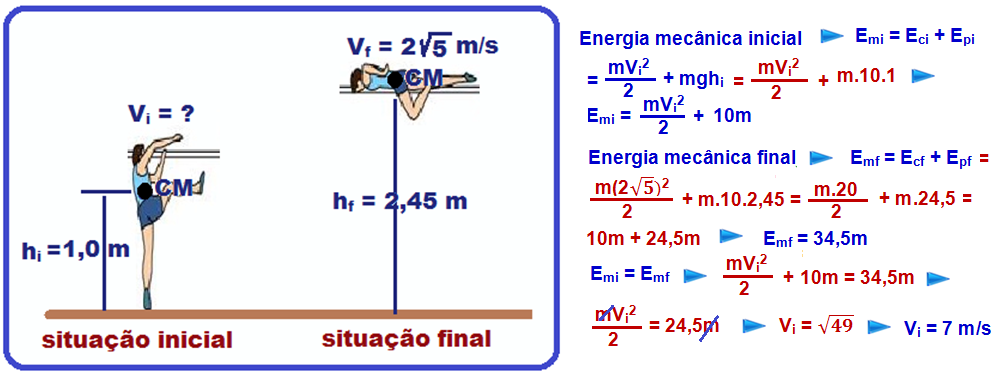
R- A
05-
Se você não domina a teoria ela está a seguir:
Segunda lei de Kepler (lei das áreas)
“ O segmento de reta imaginário que une o centro do Sol ao centro do planeta varre áreas iguais em períodos de tempo iguais”
A figura abaixo representa um planeta em órbita elíptica ao redor do Sol.
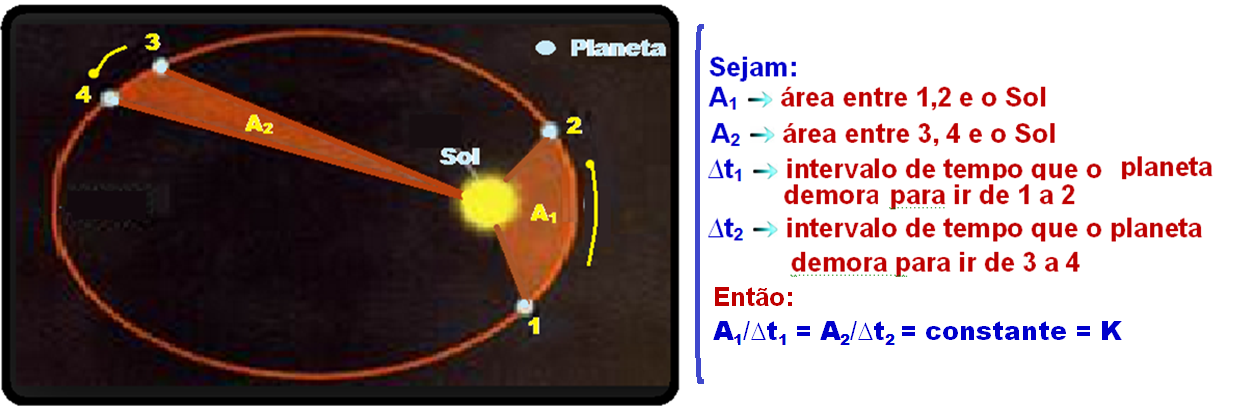
V12 > V34
Essa constante K depende do planeta e recebe o nome de velocidade areolar (velocidade escalar orbital)..
Observação importante: Observe que, quando A1 = A2 ![]() ∆t1 = ∆t2, ou seja, para o arco maior (1,2), ser percorrido no mesmo intervalo de tempo que o arco menor (3,4), a velocidade em (1,2) (mais perto do Sol, periélio) deve ser maior que a velocidade em (3,4) (mais afastado do Sol, afélio).
∆t1 = ∆t2, ou seja, para o arco maior (1,2), ser percorrido no mesmo intervalo de tempo que o arco menor (3,4), a velocidade em (1,2) (mais perto do Sol, periélio) deve ser maior que a velocidade em (3,4) (mais afastado do Sol, afélio).
Então, V12 > V34.
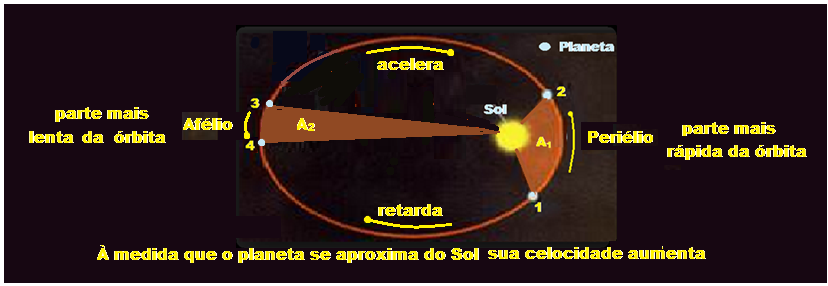
Portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio.
Ainda, de acordo com essa lei, se as órbitas forem circulares a velocidade de translação será constante e se a órbita do planeta tiver raio R e seu período de translação for T, sua velocidade areolar (velocidade escalar orbital) será constante e dada por: K = V = A/∆t = πR2 /T.
R- E
06- 
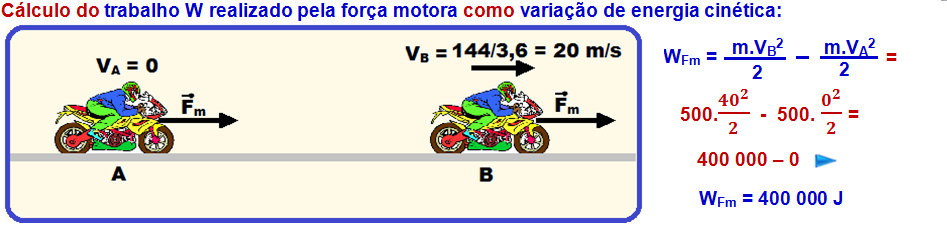
Potência = 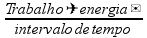
![]() 60 000 =
60 000 = 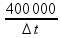
![]()
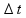 = 6, 666 s
= 6, 666 s
R- D
07-
Capacidade térmica (C) – Calor específico (c)
Define-se capacidade térmica (C) ou capacidade calorífica de um corpo como sendo o produto da massa desse corpo pelo calor específico da substância de que ele é constituído, ou seja ![]() C = m.c
C = m.c ![]() como Q = m.c.Δθ
como Q = m.c.Δθ ![]() Q = C.Δθ
Q = C.Δθ ![]() ou Q = C.(θ – θo).
ou Q = C.(θ – θo).

No caso do exercício ![]() Q = C.
Q = C.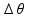
![]()
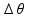 =
= 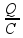 (I).
(I).
A dilatação térmica (variação de volume ∆V) sofrida pelo bloco é fornecida por ∆V = Vo. 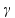 .
.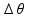 , onde o coeficiente de dilatação volumétrica
, onde o coeficiente de dilatação volumétrica 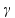 vale 3.
vale 3.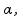 sendo
sendo 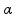 o coeficiente de dilatação linear do bloco
o coeficiente de dilatação linear do bloco ![]() ∆V = Vo.
∆V = Vo. 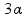 .
.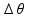 (II).
(II).
Substituindo (I) em (II) ![]() ∆V = Vo.
∆V = Vo. 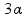 .
.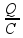 .
.
Portanto, a variação de volume ∆V do bloco é diretamente proporcional a Vo, 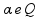 e inversamente proporcional a C.
e inversamente proporcional a C.
R- B
08-


R- C
09-
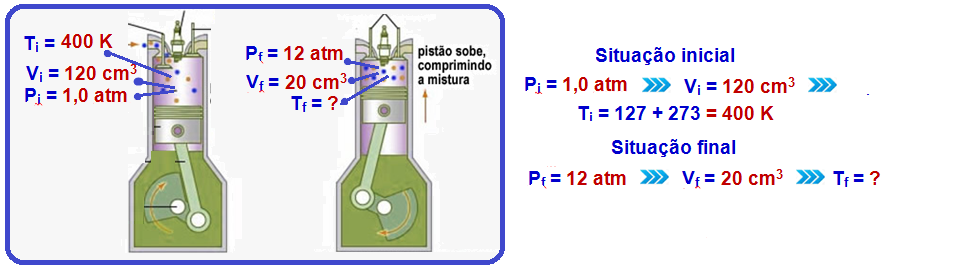
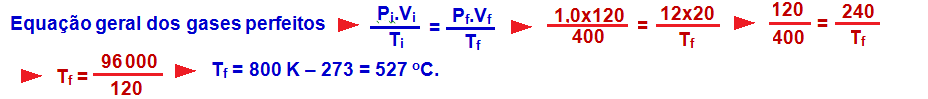
R- C
10-
Veja um resumo da teoria:
O ponto P fica em reforço (interferência construtiva), o que ocorre quando, no mesmo instante, duas cristas ou dois vales estão se superpondo.
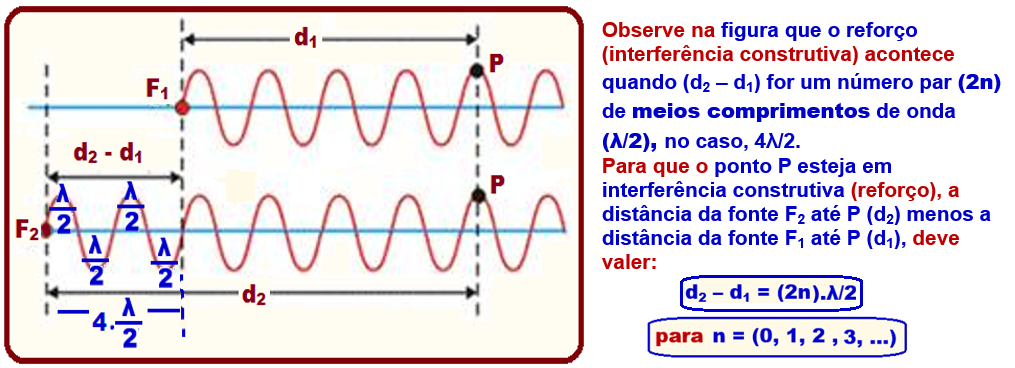
Cálculo do comprimento de onda 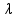 dessas ondas que possuem frequência de f = 4,0 Hz e se propagam com velocidade de V = 2,0 m/s
dessas ondas que possuem frequência de f = 4,0 Hz e se propagam com velocidade de V = 2,0 m/s ![]() V =
V = 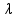 .f
.f ![]() 2 =
2 = 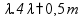
D2 = D ![]() d1 = 2, 8 m
d1 = 2, 8 m ![]()
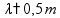
![]()
 para que D seja mínimo n = 1
para que D seja mínimo n = 1 ![]() d2 – d1 = (2n).
d2 – d1 = (2n).
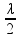
![]() D – 2,8 = (2.1).
D – 2,8 = (2.1).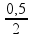
![]() D = 2,8 + 2.0,25
D = 2,8 + 2.0,25 ![]() D = 3,3 m
D = 3,3 m
R- E
11-
Equação Fotoelétrica de Einstein

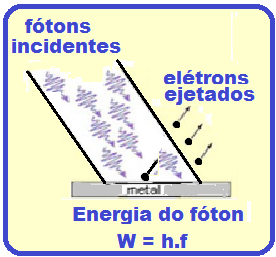
Da equação W = h.f ![]() fo = W/h
fo = W/h ![]() fo é a frequência mínima (frequência de corte) a partir da qual os elétrons são extraídos do metal.
fo é a frequência mínima (frequência de corte) a partir da qual os elétrons são extraídos do metal.
Assim, nenhum elétron é emitido pelo metal enquanto a frequência da luz (fótons) incidente não ultrapassar um certo limite de frequência, denominada frequência de corte (fo).
fo = 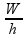
![]() fo =
fo = 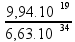
![]() fo = 1,49 Hz.
fo = 1,49 Hz.
R- C
12- A lupa é uma lente convergente e todos os raios de luz que incidem paralelamente ao eixo principal (caso do sol a pino) emergem da lente convergindo para o foco f. Assim, no caso do exercício, f = h.
Veja a construção geométrica da imagem em uma lupa (lente convergente) em que o objeto tem que estar entre fo = f = h e O.
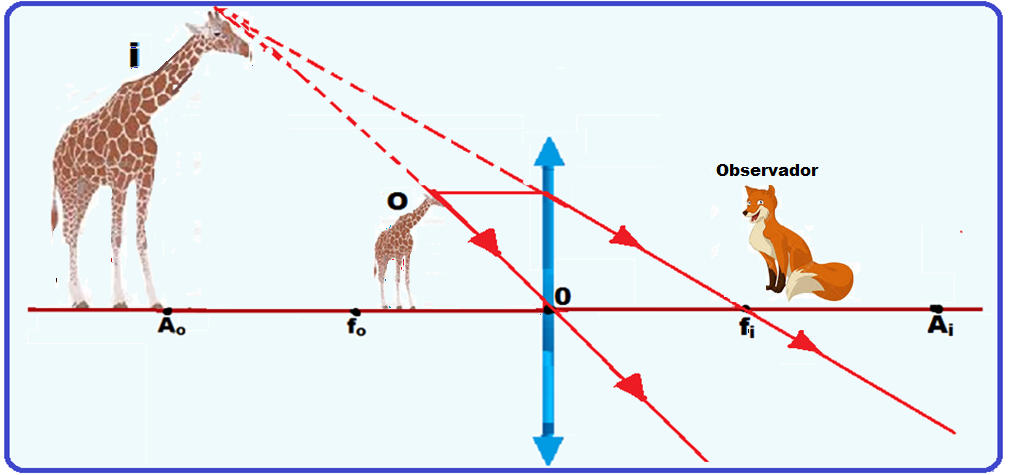
Natureza ![]() Virtual (obtida no cruzamento dos prolongamentos dos raios luminosos).
Virtual (obtida no cruzamento dos prolongamentos dos raios luminosos).
Localização ![]() Antes de fo
Antes de fo
Tamanho e orientação ![]() maior que o objeto e direita em relação a ele.
maior que o objeto e direita em relação a ele.

R- D
13-

R- B
14-
![]()
No interior do solenoide o campo magnético é praticamente uniforme e sua intensidade é constante e vale:
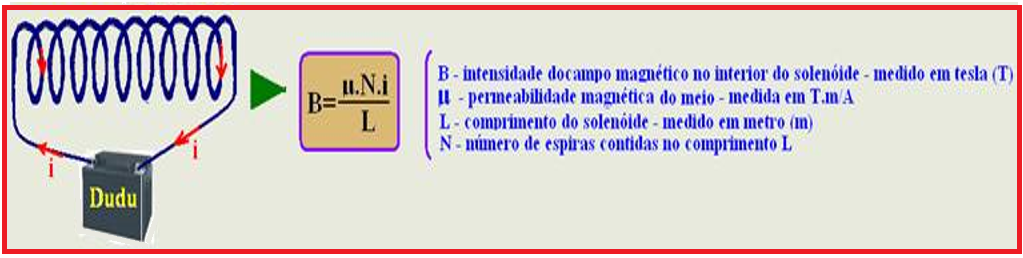
A expressão acima é válida para solenoides sem núcleo e, se você colocar no interior do solenoide
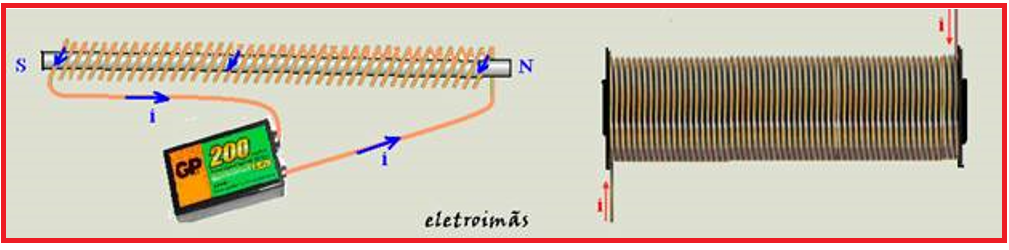
um núcleo de material ferromagnético, a intensidade do campo magnético gerado fica muito aumentada ele será um eletroímã (imã muito possante).

R – B
