Vestibular da FAMERP-2017 – Resolução
Resolução comentada das questões de Física do vestibular da
FAMERP-2017
Conhecimentos Gerais
01- Como a vazão de água é constante, para um mesmo intervalo de tempo um mesmo volume de água está caindo no interior do copo.
Assim, quanto maior for a seção transversal do copo, o mesmo volume de água despejado em seu interior, no mesmo intervalo de tempo, provocará um aumento menor de altura e quanto menor for a seção transversal do copo, o mesmo volume de água despejado em seu interior, no mesmo intervalo de tempo, provocará um aumento maior de altura.
Observe atentamente o gráfico e a figura abaixo e veja que a alternativa que melhor satisfaz é a B.
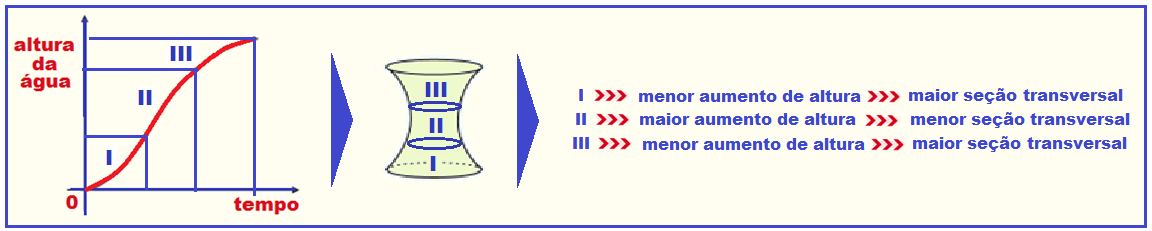
R- B
02- Sabendo que os recipientes de volumes Vmaior e Vmenor tem formatos matematicamente semelhantes seus volumes são proporcionais às qualquer uma de suas dimensões elevadas ao cubo.
Assim, são válidas as seguintes relações:
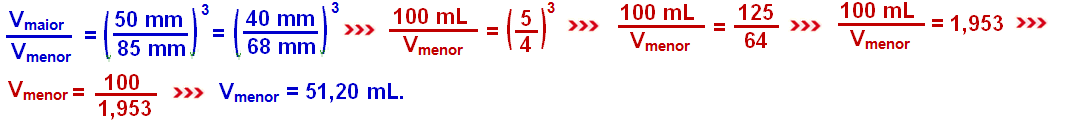
R- E
03- Como a bola sai da mesa com velocidade inicial (horizontal Vo) e cai sujeita à aceleração da gravidade g, trata-se de um lançamento horizontal.
Olhando de cima você está vendo o movimento horizontal da bola e olhando de frente, o movimento vertical da mesma.
Veja como a situação apresentada pode ser esquematizada (lançamento horizontal) com as seguintes características:
Colocando-se a origem do sistema de referência no ponto de lançamento, orienta-se, por exemplo, o eixo X para a direita e o eixo Y para baixo.
Decompõe-se o movimento em duas parcelas:
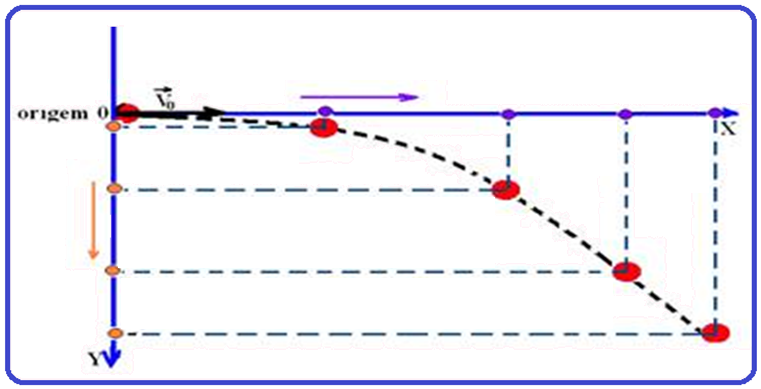
![]() Segundo o eixo X
Segundo o eixo X ![]() trata-se de um movimento horizontal uniforme com velocidade constante de intensidade Vo , que é a velocidade de lançamento
trata-se de um movimento horizontal uniforme com velocidade constante de intensidade Vo , que é a velocidade de lançamento ![]() S = So + V.t
S = So + V.t ![]() X = 0 + Vo.t
X = 0 + Vo.t ![]() X = Vo.t
X = Vo.t
![]() Segundo o eixo Y
Segundo o eixo Y ![]() trata-se de um movimento uniformemente variado com velocidade inicial
trata-se de um movimento uniformemente variado com velocidade inicial
Vo = 0, ou seja, é uma queda livre com o corpo abandonado da origem, sujeito apenas à aceleração da gravidade, de intensidade g, direção vertical e sentido para baixo.
Equações:
S = So + Vo.t + at2/2 ![]() Y = 0 + 0.t + gt2/2
Y = 0 + 0.t + gt2/2 ![]() Y = g.t2/2
Y = g.t2/2
Vy = Voy + a.t ![]() Vy= 0 + g.t
Vy= 0 + g.t ![]() Vy = g.t
Vy = g.t
V2 = Vo2 + 2.a.ΔS ![]() Vy2 = Voy2 + 2.g.Δh
Vy2 = Voy2 + 2.g.Δh ![]() Vy2 = 02 + 2.g.Δh
Vy2 = 02 + 2.g.Δh ![]() Vy2 = 2.g.Δh
Vy2 = 2.g.Δh
No caso do exercício:
Cálculo do tempo t que a bola demora para atingir o solo onde y = 1,25 m ![]() Y = g.t2/2
Y = g.t2/2 ![]() 1,25 =
1,25 =
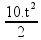
![]() t =
t = 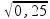
![]() t = 0,5 s.
t = 0,5 s.
Esse tempo de queda na vertical é o mesmo que a bola demora para percorrer X = 2,4 m na horizontal com velocidade Vo ![]() X = Vo.t
X = Vo.t ![]() 2,4 = Vo.0,5
2,4 = Vo.0,5 ![]() Vo = 4,8 m/s.
Vo = 4,8 m/s.
R- D
04- Peso do conjunto A ![]() PA = 4mg
PA = 4mg ![]() peso do conjunto B
peso do conjunto B ![]() PB = 2mg.
PB = 2mg.
Chamando a distância entre cada marca consecutiva de d e de Y a distância de P até onde se deve colocar o peso PB você obterá o esquema da figura abaixo:
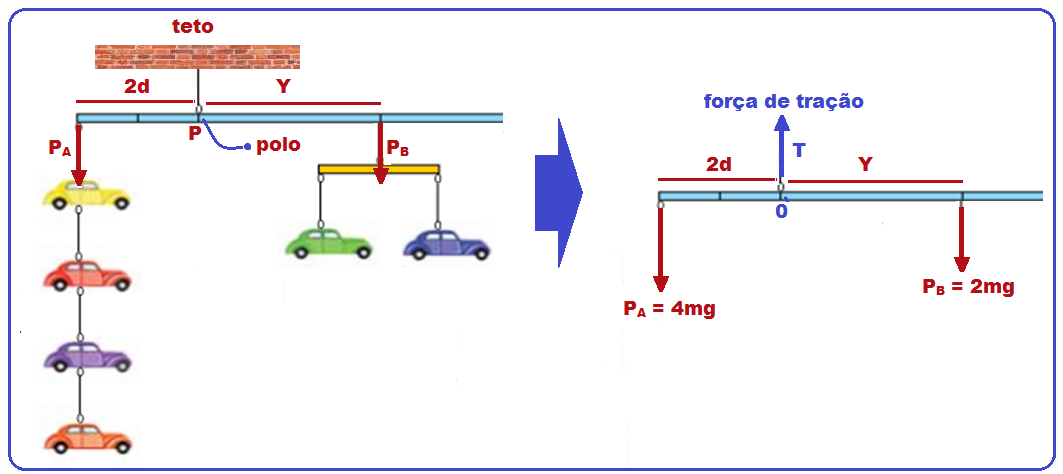
Adotando o ponto P como polo 0 (eixo de rotação) e o sentido horário de rotação como positivo e anti horário como negativo, vamos calcular o momento de cada força em relação ao polo.
MPA = – F.dPAP = – PA.2d ![]() MPA = – 4mg2d
MPA = – 4mg2d ![]() MPA = – 8mgd
MPA = – 8mgd ![]() (sinal negativo, pois tende a girar no sentido anti horário)
(sinal negativo, pois tende a girar no sentido anti horário)
MT = T.0 ![]() MT = 0
MT = 0
MPB = + F.dPPB = + PB.Y ![]() MPB = + 2mgY
MPB = + 2mgY ![]() (sinal positivo, pois tende a girar no sentido horário)
(sinal positivo, pois tende a girar no sentido horário)
A condição de equilíbrio de rotação é que a soma dos momentos de cada força em relação ao polo deve ser nula ![]() MPA + MT + MPB = 0
MPA + MT + MPB = 0 ![]() – 8mgd + 0 + 2mgY = 0
– 8mgd + 0 + 2mgY = 0 ![]() Y =
Y = 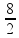
![]() Y = 4
Y = 4
R- C
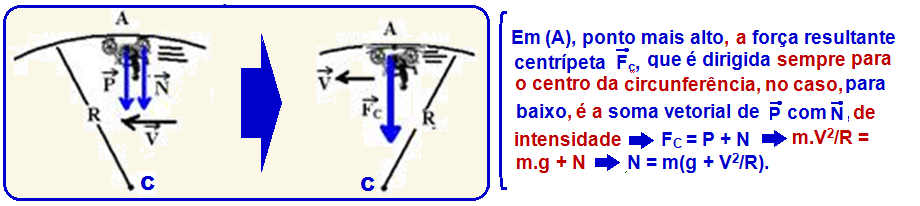
05- Veja a teoria abaixo que está relacionada com o exercício onde o avião (ou o piloto) comportam-se como a moto e a normal ![]() que a moto troca com o piso do globo pela força que o avião troca com o ar.
que a moto troca com o piso do globo pela força que o avião troca com o ar.
Globo da morte
Suponha um motociclista de massa total m (massa dele + massa da moto) descrevendo voltas segundo um plano vertical, com velocidade escalar constante ![]() no interior de uma esfera metálica oca de raio R “globo da morte”.
no interior de uma esfera metálica oca de raio R “globo da morte”.


06- Interessa a bola branca de massa m com quantidade de movimento inicial ![]() e quantidade de movimento final
e quantidade de movimento final ![]() indicadas na figura:
indicadas na figura:
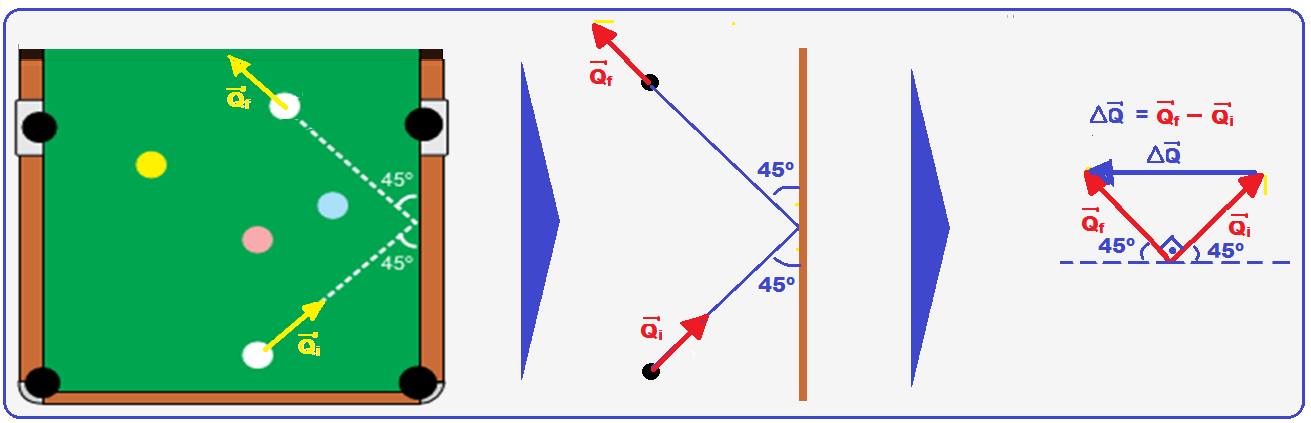

R- A
07-
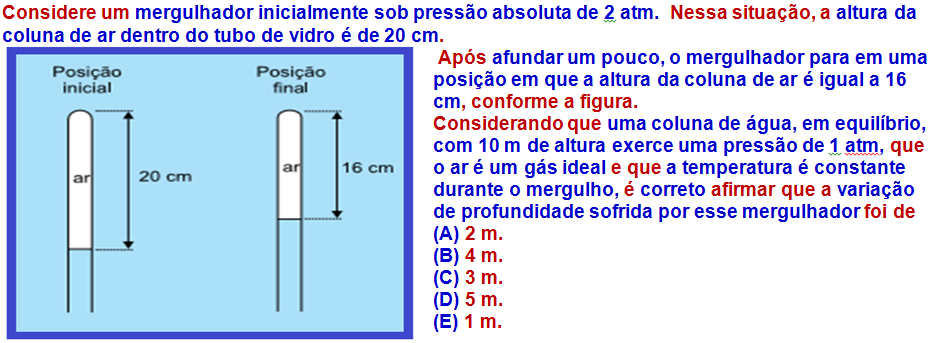
Como interessa o ar no interior do tubo vamos calcular seus volumes inicial (Vi) e final (Vf) sendo (S) a área da vase do cilindro, que é a mesma nas duas situações:


Observe que à medida que ele afundou a pressão aumentou de 2,0 atm para 2,5 atm sofrendo um acréscimo de 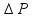 = 0,5 atm.
= 0,5 atm.
Como o enunciado considera que uma coluna de água, em equilíbrio, com 10 m de altura exerce uma pressão de 1,0 atm, ou seja, para cada 10m de aumento de profundidade a pressão aumenta de 1,0 atm então, como a pressão aumentou de 0,5 atm ele afundou 5,0 m.
R- D
08-
Índice de refração

Observe na expressão acima que, sendo a velocidade c da luz constante, a velocidade v de propagação da luz no meio (no caso, o vidro) é inversamente proporcional ao índice absoluto de refração da luz nesse meio.
A dispersão luminosa ocorre artificialmente quando a luz se dispersa como no interior de um prisma (ou no interior da esfera de vidro do exercício) ou quando passa do ar para a água, sendo mais desviada a luz monocromática violeta (menor velocidade) e menos desviada a luz monocromática vermelha (maior velocidade).
Como, pelo enunciado, o índice refração absoluto do vidro é maior para a cor azul do que para a
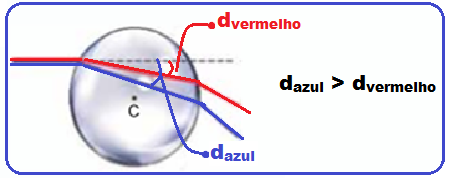
vermelha, a luz azul, no interior do vidro sofre maior desvio ao atravessar a esfera (veja figura acima).
R- B
09-
Observe atentamente nas figuras abaixo que a primeira vez que o perfil da corda será como na figura 2 será quando houver interferência destrutiva do vale do pulso 1 (ponto A) com a crista do pulso 2 (ponto B) se anulando fornecendo o perfil de onda pedido e mostrado pela linha preta.. 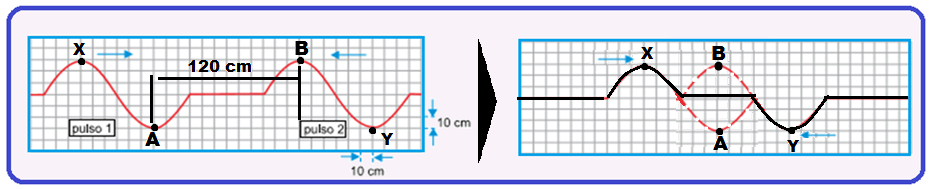
Assim, cada ponto A ou B, X ou Y deslocaram-se de 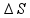 = 60 cm em sentidos contrários, cada um com velocidade fornecida de V = 60 cm/s tal que V =
= 60 cm em sentidos contrários, cada um com velocidade fornecida de V = 60 cm/s tal que V = 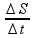
![]() 60 =
60 = 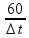
![]() ∆t =
∆t =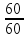 = 1 s
= 1 s
R- A
10- Lembre-se que cargas elétricas positivas criam no ponto P campos elétricos de afastamento e negativas, de aproximação.
Se a intensidade do campo elétrico criado por Q1 em P tem módulo E as outras cargas, de mesmo módulo, também originarão em P campos de intensidades E, pois E = 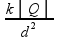 , com k,│Q│e d2 constantes.
, com k,│Q│e d2 constantes.
Veja nas figuras a representação da direção e sentido dos campos criados em P por cada carga (positiva, de afastamento e negativa, de aproximação), e a sequência do cálculo da intensidade do campo elétrico resultante ER.
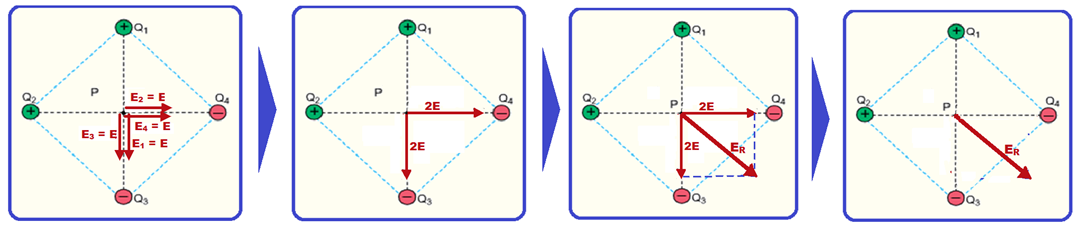
Aplicando Pitágoras na terceira figura (triângulo retângulo) ![]() ER2 = (2E)2 + (2E)2 = 2.(2E)2
ER2 = (2E)2 + (2E)2 = 2.(2E)2 ![]()
ER =2.E.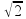
R- D
11- Observe que as duas lâmpadas acesas de mesma potência P = 60 W e sob tensão de U = 12 V estão associadas em paralelo e, ambas também em paralelo com a bateria de U = 12 V o que é óbvio, pois a tensão U é a mesma.
Assim, usando os valores nominais fornecidos a corrente elétrica i em cada lâmpada será a mesma e fornecida por P = i.U ![]() 60 = i.12
60 = i.12 ![]() i = 5 A.
i = 5 A.
Veja na figura abaixo que a corrente que passa pelo fusível deve valer if = 2.i = 2.5 ![]() if = 10 A.
if = 10 A.
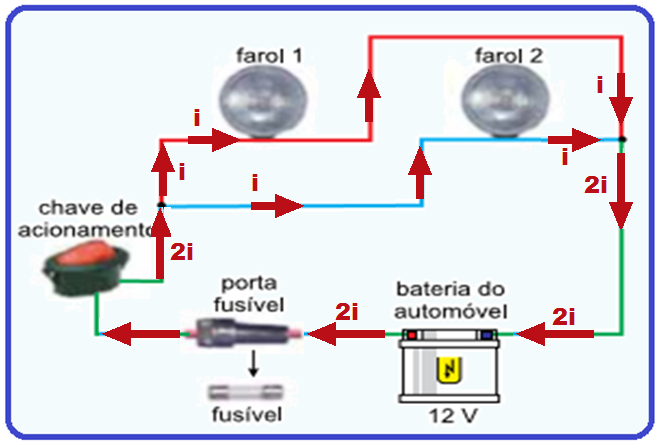
Das alternativas, aquela cujo fusível apresenta menor amperagem (intensidade de corrente elétrica)
capaz de proteger esse circuito é o de 12 A.
R- B
12- As figuras abaixo representam a posição da espira num giro anti-horário de 0o a 90o da espira:
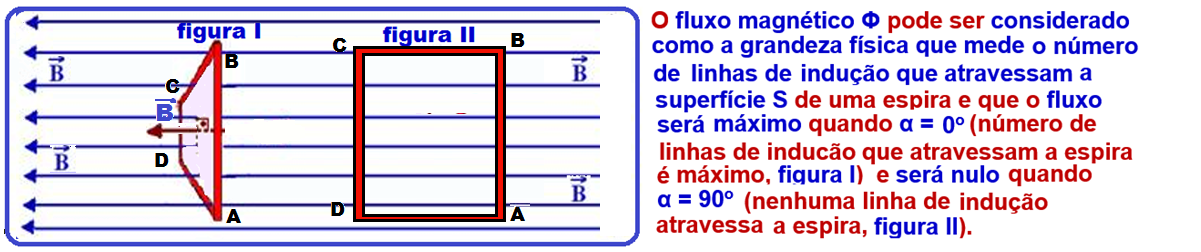 Aplicando a regra da mão direita na situação inicial (figura I) “polegar no sentido da corrente e a
Aplicando a regra da mão direita na situação inicial (figura I) “polegar no sentido da corrente e a
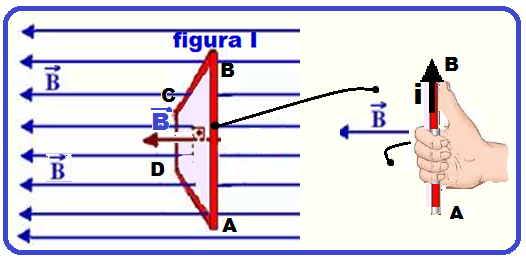
‘fechada’ da mão por dentro da espira no sentido de B” você verifica que o sentido inicial de i é ABCD.
À medida que a espira gira no sentido anti-horário a intensidade do fluxo magnético no interior da espira e consequentemente da corrente elétrica i vai diminuindo (mas mantendo o sentido ABCD) até completar o giro de 90o (figura II) quando se anulam.
R- C
Conhecimentos específicos
01-
a) Em todo gráfico Vxt o deslocamento 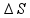 do corpo é numéricamente igual á área, nesse caso, entre os instantes 0 e 10 s que é a área de um trapézio:
do corpo é numéricamente igual á área, nesse caso, entre os instantes 0 e 10 s que é a área de um trapézio:

Mas, o enunciado não pede o deslocamento entre 0s e 10s, mas sim a posição no instante t = 10 s

e, pelo gráfico Sxt você observa que ele partiu da origem So = 0, então quando t = 10s o espaço S será ![]()
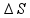 = S – So
= S – So ![]() 26 = S – 0
26 = S – 0 ![]() S = 26 m.
S = 26 m.
b) Observe no gráfico da velocidade que, entre 5s e 10 s o gráfico é uma mesma reta inclinada o que significa que nesse intervalo de tempo a aceleração tem o mesmo módulo que pode ser calculado por a = 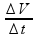 =
= 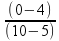
![]() a = –
a = – 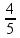
![]() em módulo
em módulo ![]() a = 0,8 m/s2.
a = 0,8 m/s2.
Pelo Princípio Fundamental da Dinâmica ou Segunda lei de Newton ![]() FR = m.a = 8.0,8
FR = m.a = 8.0,8 ![]()
FR = 6,4 N.
02-
a) O menor intervalo de tempo, em minutos, para que o satélite se movimente da posição A para a posição B, ocorre quando o satélite se move no sentido anti-horário varrendo o ângulo de 108o.
Pelo enunciado, o período do satélite (tempo que ele demora para efetuar uma volta completa em torno da Terra e percorrer um arco de 360o) é de 140 min, então para percorrer 108o basta utilizar uma regra de três:
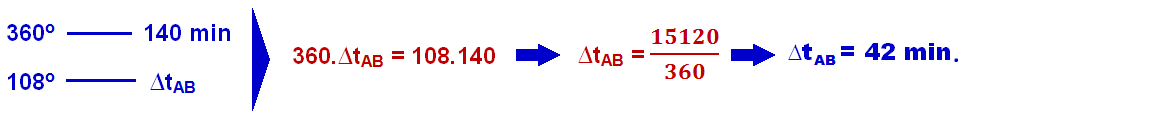
b) O raio da órbita do satélite (Ro) é medido em relação ao centro da Terra, ou seja Ro = RT + 2560 ![]() Ro = 6400 + 2650
Ro = 6400 + 2650 ![]() Ro = 8960 km.
Ro = 8960 km.
Assim, o satélite dista do centro da Terra em função ao raio da Terra R de ![]() Ro =
Ro = 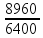 = 1,4R.
= 1,4R.
Veja no gráfico a correspondência entre essa distância (Ro =1,4R) e g:
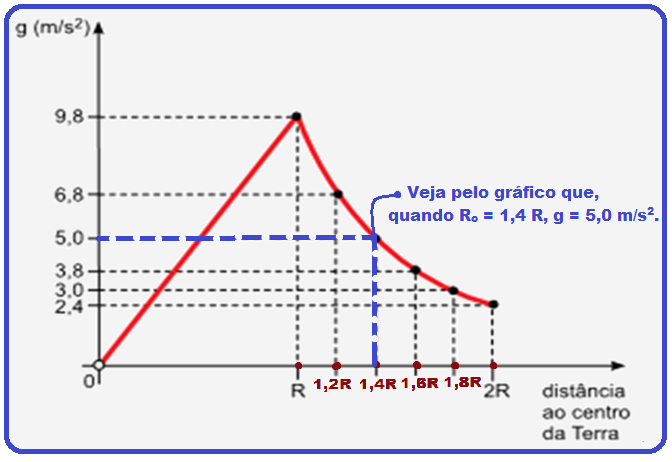
R – g = 5m/s2
03- a)
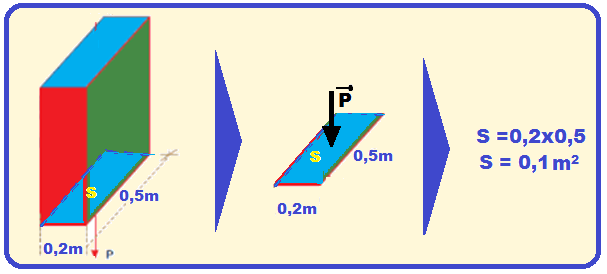
A força responsável pela pressão sobre a área S = 0,1 m2 é o peso da caixa de módulo P = m.g = 150×10 ![]() P = 1500N.
P = 1500N.
Pressão exercida pela caixa sobre a borda da piscina ![]() PR =
PR =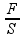 =
= 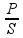 =
= 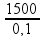
![]() PR = 15000 = 15000 N/m2
PR = 15000 = 15000 N/m2 ![]() PR = 15 kPa.
PR = 15 kPa.
b):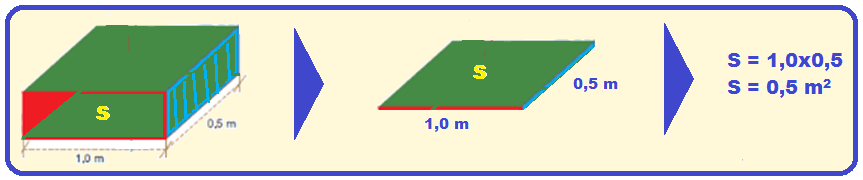
Agora, com a caixa em repouso na superfície do fundo da piscina a nova área apoiada será S = 0,5 m2.
O volume da caixa vale Vcaixa = 1,0×0,5×0,2 = 0,1 m3.
Como a caixa está totalmente imersa na água ela sofrerá um empuxo E, vertical e para cima, de intensidade E = dágua.Vcaixa.g = 103.10-1.10 ![]() E = 103 N.
E = 103 N.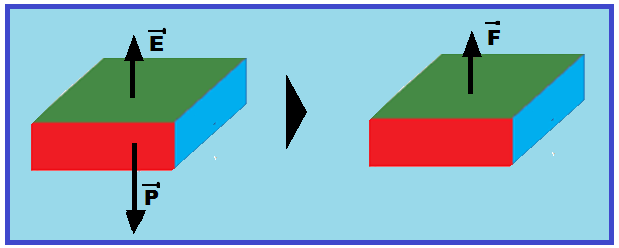
Além do empuxo age sobre a caixa seu peso P, vertical e para baixo de intensidade P = 1500 N.
Assim, a intensidade da força que a caixa aplica sobre o fundo da piscina na área de contato vale
FR = P – E = 1500 – 1000 ![]() FR = 500 N.
FR = 500 N.
PR =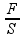 =
= 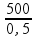 = 1000 N/m2
= 1000 N/m2 ![]() PR = 1 kPa.
PR = 1 kPa.
04-
a)

São dados:
Q1 ![]() quantidade de calor recebido da fonte quente num ciclo
quantidade de calor recebido da fonte quente num ciclo ![]() Q1 = 4,0.103 J
Q1 = 4,0.103 J
Q2 ![]() quantidade de calor rejeitado para a fonte fria num ciclo
quantidade de calor rejeitado para a fonte fria num ciclo ![]() Q2 = 2,8.103 J
Q2 = 2,8.103 J
![]()
b) Cálculo do trabalho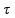 realizado em cada ciclo
realizado em cada ciclo ![]()
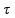 = Q1 – Q2 = 4,0.103 – 2,8.103
= Q1 – Q2 = 4,0.103 – 2,8.103 ![]()
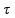 = 1,2.103 J
= 1,2.103 J
Como são 3000 ciclos o trabalho total será ![]()
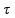 total = 1,2.103x3000
total = 1,2.103x3000 ![]()
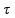 total = 3,6.106 J.
total = 3,6.106 J.

05-
a)

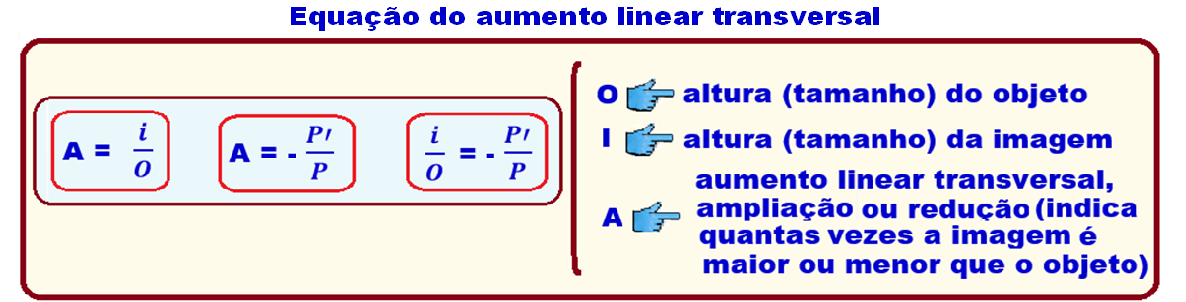
Na figura 1 a calota esférica está se comportando como um espelho esférico côncavo:
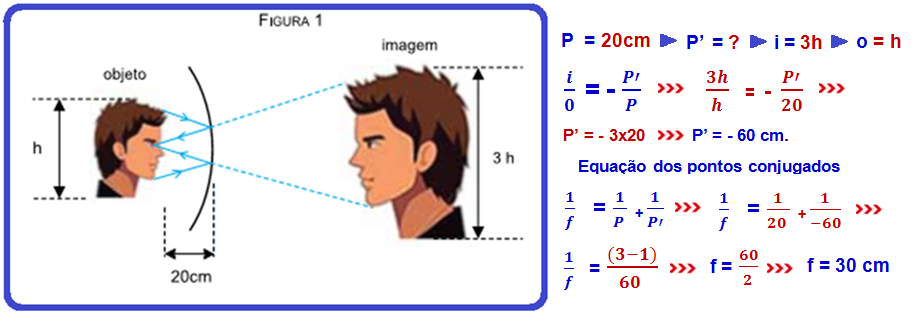
Módulo do espelho côncavo = módulo do espelho convexo = f = 30 cm.
b) Na figura 2 a calota esférica se comporta como um espelho esférico convexo de distância focal
f = – 30 cm (espelhos convexos possuem f < 0)

06-
a) Cálculo da intensidade de corrente elétrica i utilizando os valores nominais fornecidos: P = 25 W e U = 40 V ![]() P = i.U
P = i.U ![]() 25 = i.40
25 = i.40 ![]() i =
i = 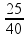 = 0,625 A.
= 0,625 A.
A carga elétrica ∆Q no intervalo de tempo ∆t = 20 minx60 = 1200 s pode ser determinada por i = 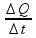
![]()
 0,625 =
0,625 = 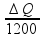
![]()
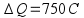 .
.
b)
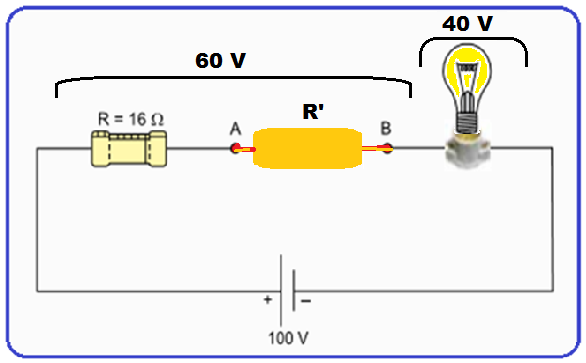
O resistor equivalente R’ (dos n resistores associados em paralelo) está ligado em série ao resistor de 16 Ω e, esse conjunto (16 Ω + R’) deve estar sob ddp de 60 V, pois a lâmpada tem ddp de 40 V e ddp total é de 100 V (veja figura ao lado).
Aplicando a lei de Ohm ao conjunto que está sob ddp de 60 V ![]() R =
R = 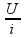
![]() (R’ + 16) =
(R’ + 16) = 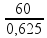
![]()
R’ + 16 = 96 ![]() R’ = 80 Ω.
R’ = 80 Ω.
Então, você deve associar em paralelo n resistores de 320Ω de maneira a obter um único resistor de 80 Ω ![]() n =
n = 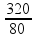
![]() n = 4.
n = 4.
