Resolução comentada da UNIFESP 2016

Resolução comentada dos exercícios do vestibular da UNIFESP – 2016

01- a) o módulo das velocidades escalares médias de A e de B, em m/s, durante os 120 s.

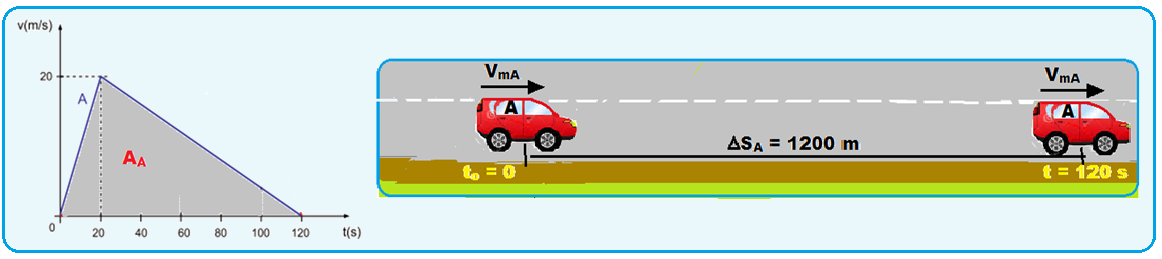
Em todo gráfico da velocidade escalar em função do tempo, a área A entre a reta representativa (linha cheia) e o eixo dos tempos é numericamente igual ao deslocamento ∆S efetuado pelo móvel em determinado intervalo de tempo ∆t.

Calculando o deslocamento do móvel A entre t_o = 0 e t = 120 s pela área A_A:

Calculando o deslocamento do móvel B entre t_o = 0 e t = 120 s pela área A_B:

b) a distância entre os veículos, em metros, no instante t = 60 s.

Observe que, no instante t = 60 s eles possuem a mesma velocidade, que é o ponto (P) onde as retas

Acontece que no instante t = 60s, V_B = V_A = V’ = 12 m/s.

Deslocamentos de A e de B entre 0 e 60 s pela área:

02- a) o módulo da força de atrito, em N, entre a caixa e a rampa no ponto B.

Observe na figura a força peso decomposta em suas duas parcelas com as respectivas funções:

Decompondo a força peso, obtemos a expressão matemática de cada uma dessas parcelas:

No caso do exercício, na rampa, a força de atrito pedida tem intensidade F_atAC = µPcosθ = µmgcosθ =

0,25.40.10.0,8 F_atAC = 80 N.

b) a distância percorrida pelo garoto, em metros, desde o ponto A até o ponto D.

Forças que agem sobre o corpo na rampa no trecho AC:

Teorema da energia cinética o trabalho de todas as forças que agem sobre o corpo no trecho total AD é igual à varação da energia cinética entre os pontos A de velocidade V_A = 1m/s e D, de velocidade zero (fornecidos pelo enunciado).

W_FatAC + W_Pp + W_FatCD = E_cD – E_cA – 800 + 2400 – 100d_CD = 0 – mV_A²/2 1600 – 100d_CD = – 40.1²/2 100d_CD = 1620 d_CD = 16,2 m.

É pedido d_AD = 10 + 16,2 d_AD = 26,2 m.

03- a) a quantidade de calor, em cal, necessária para elevar a temperatura do copo com água líquida de 20 ºC para 50 ºC.

Copo Q_c para a temperatura do copo subir de t_o = 20^oC para t = 50^oC, sendo o calor específico do copo c_c = 0,2 cal/g^oC e m_c = 200 g Q_c = m_c.c_c.(t – t_o) =100.0,2.(50 – 20) Q_c = 600 cal.

Água Q_a para a temperatura da água subir de t_o = 20^oC para t = 50^oC, sendo o calor específico da c_a = 1 cal/g^oC e m_a = 100 g Q_a = m_a.c_a.(t – t_o) = 200.1.(50 – 20) Q_c = 6000 cal.

Quantidade de calor pedida Q_t = 600 + 6000 Q_t = 6600 cal.

b) a massa de vapor de água, em gramas, necessária para elevar a temperatura do copo com água líquida até atingir o equilíbrio térmico a 50 ºC.

Pelo enunciado a temperatura inicial do vapor de água era t_o = 120 ^oC, que deve se transformar em água líquida a 50 ^oC. Etapas:

1^a Q₁ quantidade de calor cedida pelo vapor de água para passar de t_o = 120^oC para t = 100^oC, sem mudança de estado Q₁ = m_v.c_v.(t – t_o) = m_v.0,5.(100 – 120) Q₁ = – 10m_v.

2ª Q₂ quantidade de calor cedida pelo vapor de água para passar de vapor de água a 100^oC a água líquida a 100^oC (condensação, liquefação) Q₂ = m_v.L= m_V.(-540) Q₂ = – 540m_v.

3^a Q₃ quantidade de calor cedida pela água líquida para passar de t_o = 100^oC para t = 50^oC, sem mudança de estado Q₃ = m_v.c_a.(t – t_o) = m_v.1.(50 – 100) Q₃ = – 50m_v.

Quantidade de calor cedida pelo vapor de água para se transformar em água líquida a 50^oC

Q’ = Q₁ + Q₂ + Q₃ = – 10 m_v – 540m_v – 50m_v Q’ = – 600m_v.

Essa quantidade de calor Q’ cedida pelo vapor de água para ir de 120^oC a água a 50^oC é a mesma recebida pelo sistema (copo + água) para ir de 20^oC a 50^oC (achada no item Q_t = 6600 cal), ou seja, no equilíbrio térmico a soma dessas quantidades de calor trocadas entre o vapor e o copo com água deve ser nula.

– 600m_v + 6600 = 0 m_v = 6600/600 m_v = 11 g.

04- a) a distância, em metros, da imagem dos veículos ao espelho.

Existe uma relação matemática entre a posição (localização) do objeto P, a da imagem P’ e a distância focal f para os espelhos esféricos, denominada equação dos pontos conjugados, no referencial de Gauss, que é fornecida pela expressão:

b) a relação entre o comprimento do diâmetro da imagem do pneu de um dos carros, indicada por d na figura, e o comprimento real do diâmetro desse pneu.

Equação do aumento linear transversal

05- a) a resistência equivalente, em Ω.

Observe a sequência abaixo para o cálculo da resistência equivalente R_eq no circuito da figura 2, onde os três resistores estão em paralelo:

b) a potência total dissipada, em W.

Você pode calcular a potência total dissipada utilizando a resistência equivalente que está submetida à uma tensão de U = 12 V.

 

Voltar para os exercícios