Resolução Comentada USS – 2 2015
RESOLUÇÕES
01- Partiu de uma estação quando t=0 e chegou à outra quando t=120s.
Em todo gráfico Vxt o deslocamento d é numericamente igual à área, no caso, de um trapézio:
d = (B + b).h/2 = (120 + 50).15/2 = 2550/2 
d = 1275m.
R- C
02- W=Q=2,6.106kJ = 2,6.109J m = 104 kg θo = 20oC c = 4 kJ.kg-1.°C-1 = 4.103 kJ.kg-1.°C-1.
W = Q = m.c.(θ – θo) 2,6.109 = 104.4.103.(θ – 20) 2,6.109/4.107 = θ – 20 0,65.102 = θ – 20
θ = 65 + 20 θ = 85oC.
R- E
03- RA = UA/iA = 50/10 RA = 5 Ω RB = UB/iB = 120/48 RB = 2,5 Ω.
Associados em série Req = RA + RB = 5 + 2,5 Req = 7,5 Ω.
R- D
04- Em=Ec + Epg = mV2/2 + m.g.h = 8000.2502/2 + 8000.10.11000 Em = 250 000 000 + 880 000 000
Em = 250.106 + 88.106 = 1130.107 Em = 11,3.109 J.
R- D
05- Bloco1 quando a trava é retirada o bloco 1 se move com aceleração a percorrendo ∆S = 90cm
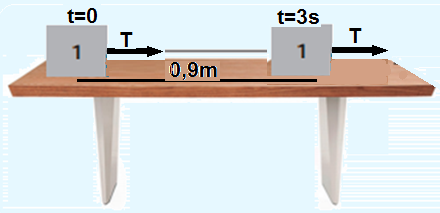
= 0,9m, partindo do repouso (Vo = 0) durante t = 3s, puxado por FR = T:
∆S = Vot + at2/2 0,9 = 0.3 + a.32/2 a = 0,9/4,5 a = 0,2 m/s2.
FR = T = m1.a T = m1.0,2 T = 0,2m1
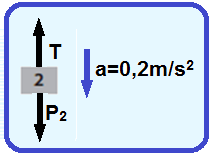
Bloco 2 está caindo com aceleração a = 0,2 m/s2 tal que P2 – T = m2.a m2g – T = m2.a
10m2 – 0,2m1 = 0,2m2 9,8m2 = 0,2m1 m1/m2 = 9,8/0,2 = 49.
R- C