Resolução Comentada IFCE 2015
RESOLUÇÕES
01- Quando h = 30m e t= 2s e ela encontra-se pela primeira vez (na subida) a 30 m do solo, lançada com velocidade inicial Vo, num local onde g=10m/s2 
h = ho + Vot – gt2/2 30 = 0 + Vo.2 – 10.22/2 30 + 20 = 2Vo Vo = 25 m/s.
Velocidade com que ela passa pela altura de 30 m pela primeira, com Vo = 25 m/s e t = 2 s.
V = Vo – gt = 25 – 10.2 V = 25 – 10.2 = 5 m/s.
Se ela passa pela altura de 30m na subida com velocidade de V= + 5m/s, na descida ela passará
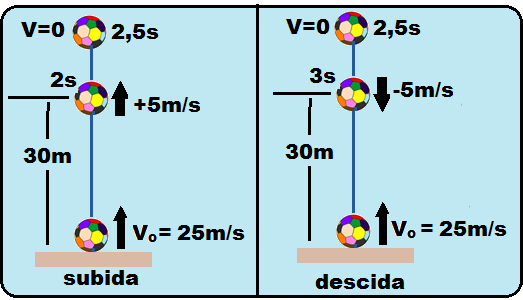
pela mesma altura (30m) com velocidade de V = – 5 m/s, no instante t’ dado por V = Vo – 10t’
-5 = 25 – 10t’ 10t’ = 30 t’ = 3 s.
R- B
02- Cálculo da densidade linear μ da corda sendo dados m=10 g = 10.10-3 = 10-2 kg e L = 26cm =
26.10-2m μ = m/L = 10-2/26.10-2 μ = 1/26 kg/m.
Velocidade V de propagação da onda na corda sendo dados f = 260 Hz e λ = 2 cm =2.10-2 m V = λ.f = 2.10-2.260 V = 520.10-2 V = 5,2 m/s.
V = √(T/μ) 5,2 = √(T/(1/26) = √(26T) (5,2)2 = [√(26T)]2 27,04 = 26T T = 27,04/26 = 1,04 N.
R- E
03- 
R- A
04- Veja tabela abaixo:
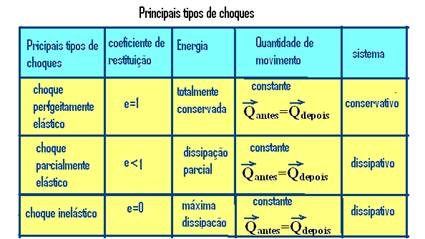
Colisão inelástica
Neste tipo de choque a dissipação de energia é máxima, o coeficiente de restituição é nulo, e, após o choque, os corpos obrigatoriamente se juntam e se movem unidos com a mesma velocidade. Lembre-se de que em qualquer tipo de choque a quantidade de movimento sempre se conserva.
No caso do exercício, a alternativa correta é a C. Justificando:
C) perfeitamente inelástica, podemos ter energia cinética final igual a zero, no caso de uma colisão frontal entre dois corpos de mesma massa e velocidades iguais em módulo, porém sentidos contrários.
Veja figura abaixo:
Antes Qsa =m(+V) + m(-V) = + mV – mV Qsa = 0
Depois Qsa = Qsd = 0 Ecd =2mV2/2 = 2m.02/2 Ecd = 0.
R- C
05- QA e QB cargas antes de colocar o fio e Q’A e Q’B, cargas depois de colocar o fio:
QA + QB = Q’A + Q’B 20μ + 40μ = Q’A + Q’B 60μ = Q’A + Q’B (I)
Q’A/RA = Q’B/RB Q’A/1.10-2 = Q’B/3.10-2 Q’B = 3Q’A (II)
(II) em (I) Q’A + 3Q’A = 60 μ Q’A = 60/4=15 μC Q’B = 45 μC
R- D