Resolução Comentada da UFRGS 2015
RESOLUÇÕES
01- 1° caso: se os dois móveis estiverem andando no mesmo sentido, o valor da velocidade relativa é dado pelo módulo da diferença entre os módulos das duas velocidades escalares. Dessa forma, temos:
|vrel |= |vA |- |vB |
2° caso: se os dois móveis estiverem andando em sentidos contrários, o valor absoluto da velocidade relativa é dado pela soma dos módulos das duas velocidades escalares. Assim, temos:
|vrel |= |vA |+ |vB |
No caso do exercício eles se movem em sentidos contrários 
|vrel |= |vA |+ |vB | = |360 |+ |360 |
|vrel | = 720 km/h/3,6 = 200 m/s.
R- C
02- Vo = 0 V = 540/3,6 = 150m/s ∆t = 2,5minx60 = 150s a = ∆V/∆t = (150 – 0)/150 a = 1m/s2.
R- B
03- Trata-se de um lançamento oblíquo onde,na vertical (Y) você tem as funções(equações), com os respectivos gráficos
Equação da posição (dos espaços) ou da altura Y
S=So + Vo.t + a.t2/2 — Y=Yo + Voy.t – gt2/2 — Y=0 + Voy.t – gt2/2 — Y= Voy.t – gt2/2, com Voy=Vo.senα
Equação da velocidade Vy
V=Vo + a.t — Vy=Voy – g.t, com Voy=Vo.senα
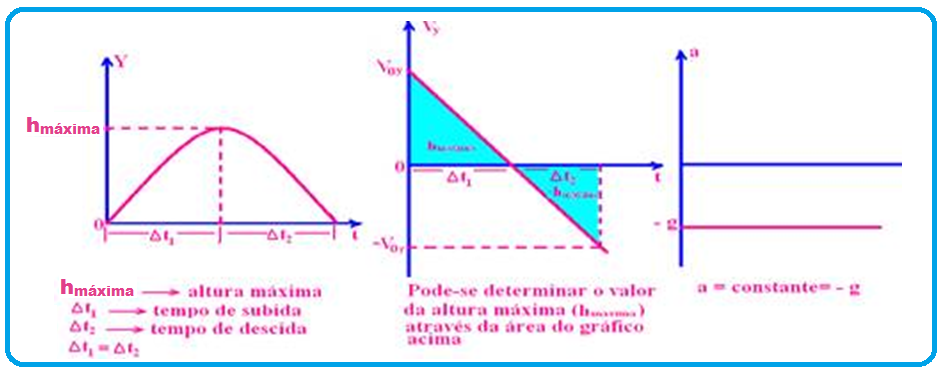
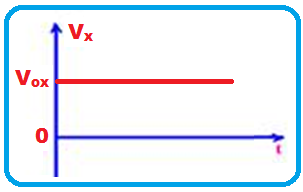
Movimento parcial na direção horizontal (eixo X)
Sendo o movimento apenas na horizontal, a projeção do vetor aceleração da gravidade (
) no eixo X é nula e, nesse caso o movimento é uniforme (MU) com velocidade constante Vox, de equação X = Voxt e cujo gráfico da velocidade Vx , constante, é uma reta paralela ao eixo dos tempos:
R- B
04- I. Correta Segunda lei de Kepler (lei das áreas)
“ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas
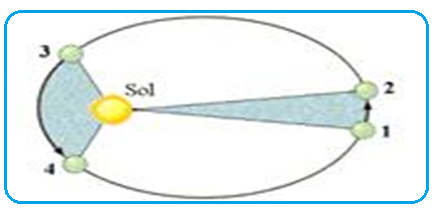
proporcionais aos tempos gastos para percorrê-las”
O enunciado afirma que o planeta percorre esses intervalos de posições em tempos iguais.
II. Falsa Terceira lei de Kepler (lei dos períodos)
“ Os quadrados dos períodos T de revolução dos planetas (tempo que demora para efetuar uma volta completa em torno do Sol) são proporcionais aos cubos das suas distâncias médias R ao Sol”
T2/R3=constante=K.
No caso do exercício R=P T2 = kP3 o correto seria: o quadrado do período da órbita é proporcional a p3 .
III. Correta Pela lei das áreas: “ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais aos tempos gastos para percorrê-las”
Então:
A1/∆t1~A2/∆t2=constante=K
Observe na expressão acima que quando A1=A2 ∆t1= ∆t2, ou seja, para o arco maior 3,4, ser percorrido no mesmo intervalo de tempo que o arco menor 1,2, a velocidade em 3,4 (mais perto do Sol – periélio) deve ser maior que a velocidade em 1,2 (mais afastado do Sol – afélio).
Portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio.
R- C
05- Em todo gráfico Fxt o impulso recebido pela aplicação da força é numericamente igual à área sob a curva I = área = (B + b).h/2 = (2 + 1).4/2 = 12/2 I = 6 N.s.
O teorema do impulso afirma que o impulso é igual à variação da quantidade de movimento (momentum linear) I = ∆Q = 6 N.s ∆Q = m∆V = m (V – Vo) 6 = 1.(V – 3) V = 6 + 3 = 9 m/s.
R- E
06- Colocando as forças que agem sobre cada bloco, na direção do movimento:
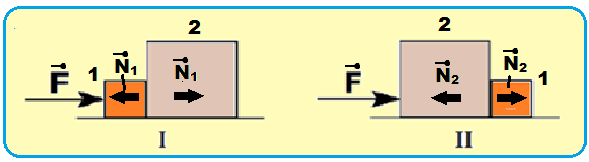
I bloco 1 FR1 = m1.a1 F – N1 = m1.a1 (I)
I bloco 2 FR = 3m1.a1 N1 = 3m1.a1 (II)
(I) + (II) F = 4m1a1 a1 = F/4m1 (III) (III) em (I) N1 = 3m1.(F/4m1) N1 = 3F/4
II bloco 1 FR2 = m1.a2 N2 = m1.a2 (I)
II bloco 2 FR2 = 3m1.a2 F – N2 = 3m1.a2 (II)
(I) + (II) F = 4m1a2 a2 = F/4m1 (III) (III) em (I) N2 = m1.(F/4m1) N2 = F/4
R- D
07- Cálculo da velocidade com que o pêndulo X (partindo de P) atinge o pêndulo Y (em Q), imediatamente antes da colisão, pelo teorema da conservação da energia mecânica:
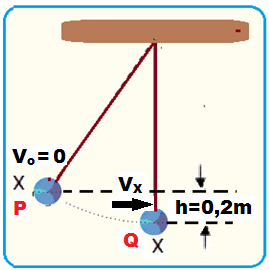
EmXP = mVX2/2 + mgh = 0,1.02/2 + 0,1.10.0,2 = 0 + 0,2 EmXP = 0,2 J.
EmXQ = mVY2/2 + mgh = 0,1.VY2/2 + 0,1.10.0 = 50VY2 + 0 EmXQ = 0,05VY2.
EmX = EmY 0,2 = 0,05VY2 VXQ = V = 2 m/s.
Utilizando a conservação da quantidade de movimento antes e depois da colisão:
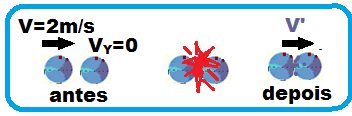
Qsa = mXV + MYVY = 100.2 + 100.0 Qsa = 200 kgm/s.
Qsd = mXV + MYVY = 100.V’ + 100.V’ Qsa = 200V’.
Qsa = Qsd 200 = 200V’ V’ = 1m/s = V/2.
R- E
08- Trabalho como variação de energia potencial gravitacional WP =mgh = 0,1.10.0,2 = 0,2 J.
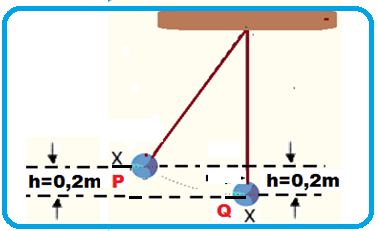
R- B
09- Energia mecânica do bloco no ponto P = energia potencial elástica armazenada pela mola quando ela está comprimida de x no ponto P EmP =Epe = kx2/2.
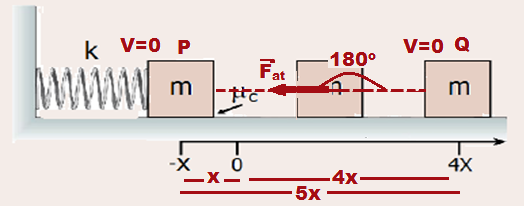
Energia mecânica do bloco no ponto Q, onde está em repouso EmQ = 0.
Toda essa energia dissipada entre os pontos P e Q (∆Em) corresponde ao trabalho da força de atrito (Wfat) nesse percurso de d= 5x ∆Em = Wfat (0 – kx2/2) = Fat.d.cosα – kx2/2 =μPdcos180o
– kx2/2 = μmg5x(-1) kx2/2 = 5μmgx x = 10μmg/k.
R- E
10- Quanto ao peso como são feitos de mesmo material e R é maciço e S oco, a massa de R é maior que a massa de S e, sendo P = mg (com g constante), PR > PS.
Quanto ao empuxo que é fornecido por E = dágua.Vágua deslocada.g dágua é a mesma, como eles possuem o mesmo volume (independente do formato) o Vágua deslocada é o mesmo e a aceleração da gravidade g é a mesma. Portanto ER = ES.
R- B
11- Aplicando a equação geral dos gases perfeitos simultaneamente aos três estados:
PMVM/TM = PNVN/TN = PRVR/TR 6.105.0,1/TM = 4.105.0,2/TN = 2.105.0,3/TR 0,6/TM = 0,8/TN = 0,6/TR
TM/3 = TR/3 = TN/4 TM = TR < TN.
R- E
12- Situação I X está eletrizada com carga positiva e Y, neutra. Quando são aproximadas, X e Y são atraídas por indução eletrostática.
Se você não domina a teoria, ela está a seguir:
Aproxima-se um condutor eletrizado, por exemplo, negativamente de um condutor neutro, sem encostar, mas bem próximos (figura 1).
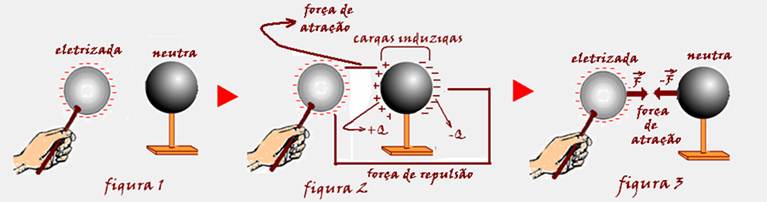
Os elétrons livres do indutor serão repelidos, ficando o lado direito do induzido com excesso de elétrons e o lado esquerdo com falta de elétrons, fenômeno que recebe o nome de indução elétrica (figura 2). Observe na figura 2 que a força de atração entre as cargas negativas e positivas é maior que aforça de repulsão entre as cargas negativas porque a distância entre as cargas que se atraem é menor e, quanto menor a distância entre cargas de mesmo módulo, maior a força entre elas.
Portanto, um corpo eletrizado pode atrair um corpo neutro, figura 3.
Situação II Trata-se de eletrização por indução. Veja teoria abaixo:
Aproxima-se um condutor eletrizado, por exemplo, negativamente. (indutor) de um condutor neutro que se deseja eletrizar (induzido), sem encostar, mas bem próximos (figura 1).
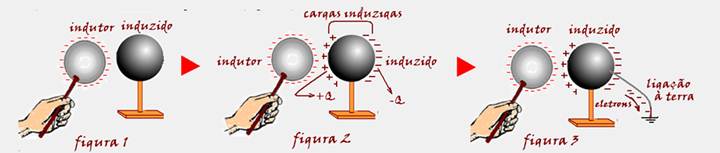
Os elétrons livres do indutor serão repelidos, ficando o lado direito do induzido com excesso de elétrons e o lado esquerdo com falta de elétrons, fenômeno que recebe o nome de indução elétrica (figura 2). As cargas elétricas que se concentram nas duas extremidades opostas (denominadas cargas induzidas) são de mesmo módulo, mas de sinais opostos e, por esse motivo o induzido continua neutro. Em seguida, ainda na presença do indutor você liga o induzido à terra (fio terra ou com seu dedo) e observa que elétrons se deslocam do induzido para a terra (figura 3). Afastando agora o indutor para bem longe, as cargas
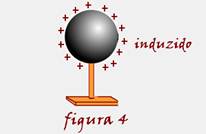
elétricas se repelem e espalham pela superfície externa do induzido, que fica eletrizado com cargas de sinal oposto ao do indutor (figura 4)
Se o indutor tivesse cargas positivas, ao final de todo o processo o induzido ficaria eletrizado com cargas negativas.
R- C
13- Segunda lei de Ohm R = ρL/A.
Resistor 1 R1 = ρ2L/A resistor 2 R2 = ρL/2A.
Resistor equivalente Req = R1 + R2 = ρ2L/A + ρL/2A = 5ρL/2A.
Req = V/i i = V/Req = V/5ρL/2A i = 2AV/5ρL.
R- A
14- Radiação alfa (α): também chamada de partículas alfa ou raios alfa, são partículas carregadas por dois prótons e dois nêutrons, sendo, portanto, núcleos de hélio. Apresentam carga positiva +2 e número de massa 4.
Radiação beta (β): raios beta ou partículas beta, são elétrons, partículas negativas com carga – 1 e número de massa 0.
Radiação Gama (γ): ou raios gama. O comprimento de onda desta radiação varia de 0,5
a 0,00 (unidade de medida: angstron). As radiações gama são ondas eletromagnéticas, e possuem carga e massa nulas, emitem continuamente calor e têm a capacidade de ionizar o ar e torná-lo condutor de corrente elétrica
Quando as partículas penetram no campo magnético, todas tem velocidade vertical e para cima — o campo magnético B penetra no papel — pela regra da mão esquerda a força que age sobre a carga positiva é horizontal e para a esquerda (é a α) — portanto a carga positiva é desviada para a
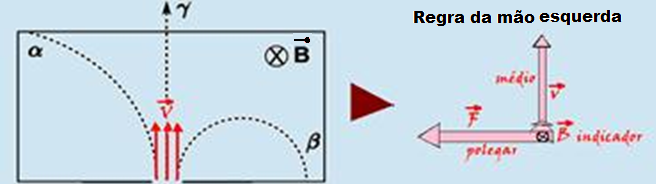
esquerda — na carga negativa o sentido dessa força é invertido — ela sofre desvio para a direita (é a β) — a neutra não sofre desvio — a neutra não sofre desvio (é a γ) — observe que o desvio da α é menor, ou seja, ela possui maior inércia e consequentemente maior quantidade de movimento e maior massa.
R- D
15- Caso particular da refração da luz todo raio de luz que incide perpendicularmente (radialmente) sobre a superfície de separação de dois meios homogêneos e transparentes (no caso, ar-vidro) não sofre desvio e passa pelo ponto O (centro da placa semicircular).
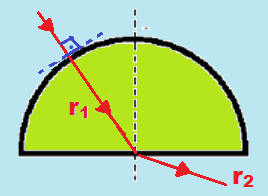
Ao sair para o ar passando de um meio mais refringente para outro menos refringente, o raio de luz aumenta a velocidade se afastando da normal.
R- A
16- Essa força eletromotriz de 1V gerada pela variação de fluxo magnético no interior do circuito provoca uma diminuição de 1V na ddp da bateria, pois se opõe a ela (lei de Lenz), fazendo com que o circuito fique sujeito a uma ddp de U = 3 – 1 = 2V.
R = U/i 2 = 2/i i = 1 A.
R – C
17- I – incorreta. As ondas P e Q possuem a mesma amplitude AP = AQ (veja figura)
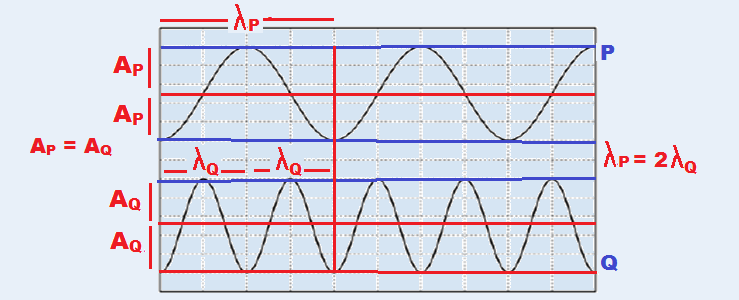
II – correta (veja figura).
III – incorreta pelo enunciado as velocidades de propagação são iguais VP = VQ = V
VP =λP.fP = 2λQ λQ fP = V/2λQ (I) VQ = λQ.fQ fQ = V/λQ (II).
(I)/(II) fP/fQ = V/2λQ X λQ/V fQ = 2fP.
R- B
18- Efeito fotoelétrico – Heinrich Rudolf Hertz, em 1887, detectou e gerou em laboratório, em uma
série de experiências que, quando a luz (onda eletromagnética, radiação eletromagnética) de freqüência suficientemente alta incide sobre a superfície de um metal, ela pode retirar elétrons do mesmo. Esse fenômeno ficou conhecido como efeito fotoelétrico.
A luz tem caráter dual: os fenômenos de reflexão, refração, interferência, difração e polarização da luz podem ser explicados pela teoria ondulatória e os de emissão e absorção podem ser explicados pela teoria corpuscular.
R- D
19- O físico francês Louis de Broglie apresentou, em 1924, a seguinte hipótese que, depois, em 1927
foi comprovada experimentalmente: “partículas também possuem propriedades ondulatórias” — das equações E=m.c2 — c – velocidade da luz no vácuo — E=h.f — c=λf — f=c/λ — mc2=hf — mc2=hc/λ — λ=h/mc — mc=Q – quantidade de movimento — a quantidade de movimento Q=m.v evidencia o caráter corpuscular da luz enquanto que o comprimento de onda λ evidencia seu caráter ondulatório.
As naturezas ondulatória e corpuscular da luz são complementares e não antagônicas
No caso do exercício λ=h/mc c=v λ = 6,6.10-34/9.10-31.2,2.106 = 3,3.10-10 m.
R- A