Resolução comentada da UFJF 2015
RESOLUÇÕES
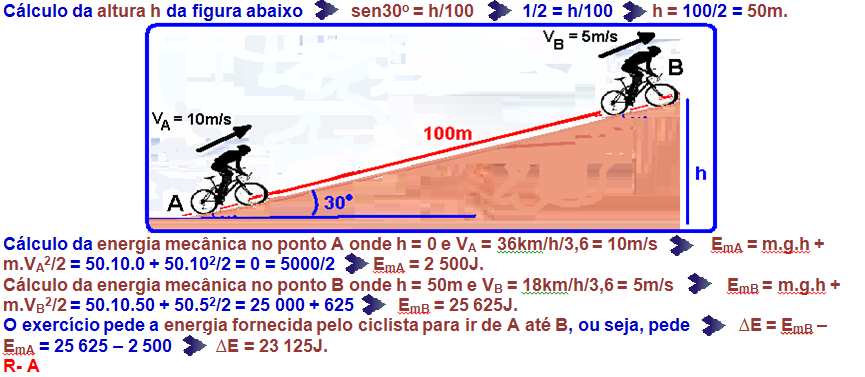
01-
02- A seguir, a teoria:
Primeira lei de Kepler (lei das órbitas)
“As órbitas que os planetas descrevem ao redor do Sol são elípticas, com o Sol ocupando um dos focos da elipse”.
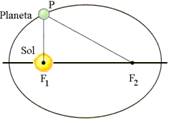
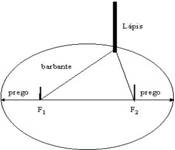
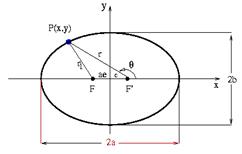
Numa elipse (figura acima), para qualquer posição do ponto P a soma das distâncias FP com PF’ é sempre a mesma.
Segunda lei de Kepler (lei das áreas)
“ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas iguais em intervalos de tempo iguais”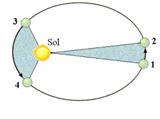
Sejam:
A1 — área entre 1,2 e o Sol
A2 — área entre 3, 4 e o Sol
∆t1 — tempo que o planeta demora para ir de 1 a 2
∆t2 — tempo que o planeta demora para ir de 3 a 4
Então:
A1/∆t1~A2/∆t2 = constante = K
Terceira lei de Kepler (lei dos períodos)
“ Os quadrados dos períodos T de revolução dos planetas (tempo que demora para efetuar uma volta completa em torno do Sol) são proporcionais aos cubos das suas distâncias médias R ao Sol”
T2/R3 = constante = K’
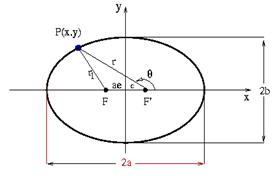
O raio médio R da órbita de um planeta corresponde à média aritmética entre a distância do Sol ao afélio e a distância do Sol ao periélio. Observe que esse valor é o mesmo que a medida do semi-eixo maior da elipse, que na figura acima seria a.
R- C
03- Todas estão corretas — veja fisicaevestibular.com.br – mecânica – dinâmica – estática.
R- E
04- a) Falsa — se ele está em movimento circular então sobre ele atua uma força resultante centrípeta, não importando se o movimento é circular uniforme ou não.
b) Falsa — pode existir forças sim, apenas que a soma vetorial dessas forças deve ser nula.
c) Correta — desde que essa força seja a força resultante, pois, pela segunda lei de Newton F = m.a.
d) Falsa — as forças de ação e reação jamais se anulam, pois são aplicadas em corpos diferentes.
e) Falsa — ela é uma força resultante, que obriga o corpo a efetuar movimento circular.
R- C
05- Distância percorrida pela Lua ao efetuar uma volta completa ao redor da Terra — ∆S = 2.п.R = 2x3x
3,8.108 — ∆S = 22,8.108 m.
Tempo que demora para efetuar uma volta completa — ∆t = 27,3 diasx24=655,2hx3600=2358720
∆t ≈ 2,36.106 s.
V = ∆S/∆t = 22,8.108/2,36.106 — V = 9,7.102 m/s.
ac= V2/R = (9,7.102)2/3,8.108 = 94,1.104/3,8.108 — ac =24,8.10-4 = 2,48.10-3 m/s2.
R- C
06- P = 23cm
F = 10cm
P’ = ?
1/f = 1/P + 1/P’ — 1/10 = 1/23 + 1/P’ — 1/10 – 1/23 = 1/P’ — (23 – 10)/230 = 1/P’ — P’ = 230/13
P’ = 17,69 cm (P’ > imagem real).
i/o = -P’/P — i/o = – 17,69/23 = – 0,8 — i = – 0,8 o — ( a imagem é invertida e 80% do tamanho do objeto)
Você pode também traçar os raios de luz e determinar as características da imagem — veja que o objeto está a 23cm da lente, ou seja, antes do dobro da distância focal (ponto antiprincipal Ao) que é de 20cm:
Objeto P antes de Ao
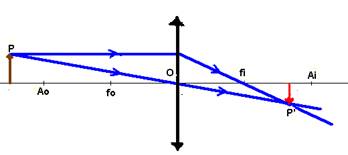
Características da imagem P’:
Natureza – Real (obtida no cruzamento do próprio raio luminoso (linha cheia)
Localização – entre Fi e Ai
Tamanho e orientação – menor que o objeto e invertida em relação ao mesmo
R- A.
07- Para a água, por exemplo, e o volume diminui na fusão e, portanto, aumenta na solidificação.
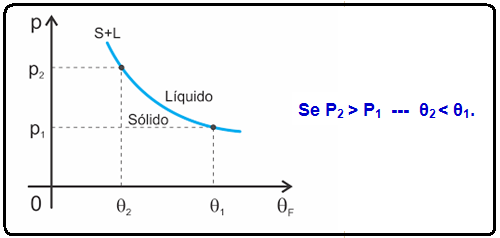
Para elas, um aumento de pressão acarreta uma diminuição na temperatura de fusão.
R- C
08- Na Celsius você tem 4 intervalos de 5cm que equivalem a 100oC/4 = 25oC que, somados a 0oC fornecem 25oC.
Na Fahrenheit você tem 4 intervalos de 5cm que equivalem a 180oC/4 = 45oC que, somados a 32oF fornecem 77oF.
R- A
Voltar para os Exercícios
