Resolução comentada da FAMERP 2015
RESOLUÇÕES
01-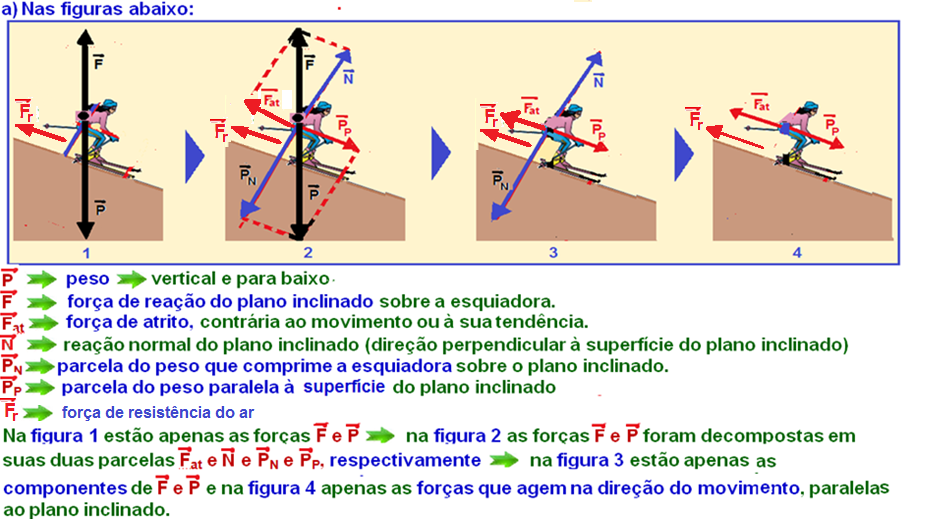 
02-) a) Observe na figura abaixo que, depois que o objeto foi preso à mola que estava em seu comprimento natural de 20cm, ela foi deformada com seucomprimento passando para 25cm e
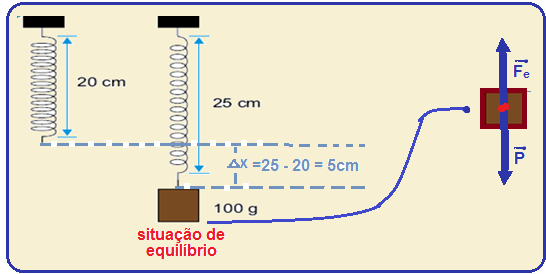
sofrendo uma deformação de ∆x = 5cm = 0,05m, quando atingiu a situação de equilíbrio.
Na situação de equilíbrio, as forças que agem sobre o objeto são, seu peso (vertical e para baixo) e a força elástica (vertical e para cima), que sustenta o objeto, que está em equilíbrio, mas não em repouso (força resultante sobre ele é nula).
b) Suponha que o objeto seja elevado até a altura em que o comprimento da mola volta a ser 20 cm e, em seguida, solto a partir do repouso. Determine a energia cinética do objeto, em joules, no instante em que passa pelo ponto em que o comprimento da mola é de 25 cm. Despreze qualquer perda de energia mecânica.
b) Cálculo da energia mecânica no ponto P onde, pelo enunciado partiu do repouso VP = 0 e se encontra na altura de h=0,05m em relação ao ponto Q tomado como referencial. Nesse ponto , a mola está em sua posição natural e não existe energia potencial elástica armazenada.
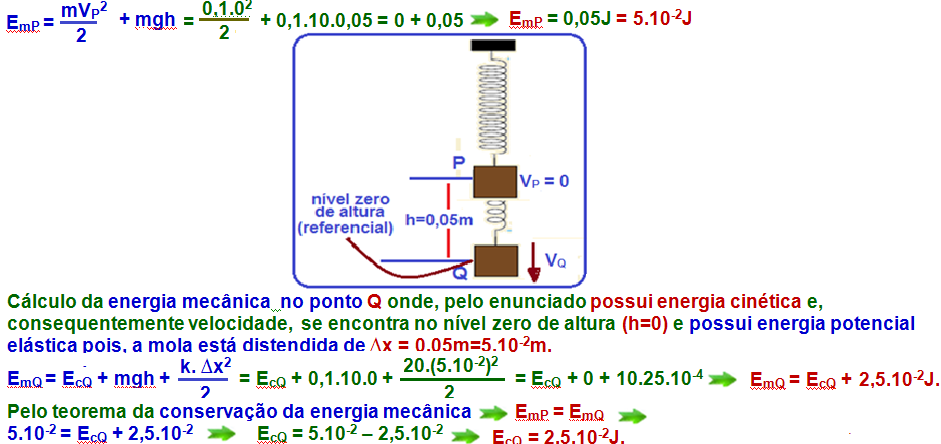
03-
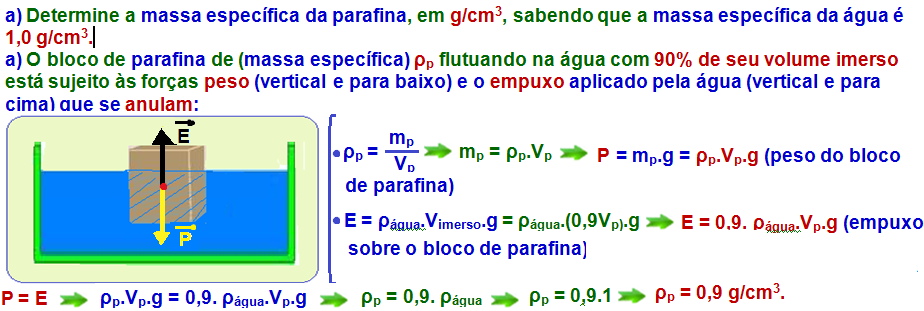
b) Que volume de álcool, em cm3, deve ser misturado à água do recipiente para que o topo do bloco passe a coincidir com a superfície do líquido? A massa específica do álcool é 0,80 g/cm3.
04- a) Calcule a distância focal da lente, em cm.
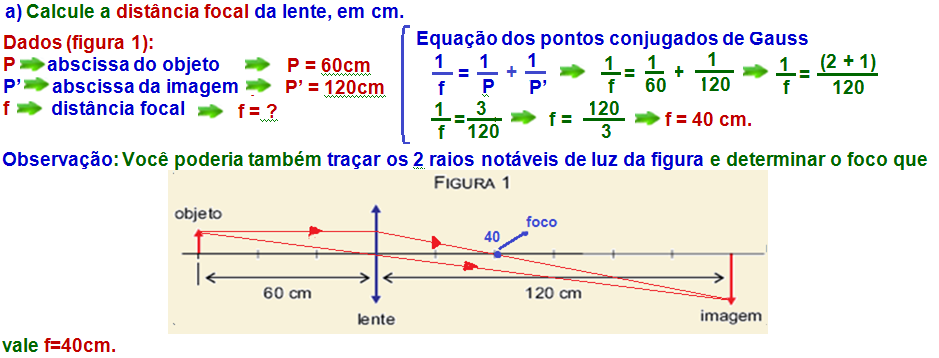
Observação: Você poderia também, na figura 2, traçar o seguinte raio notável para localizar a lente:
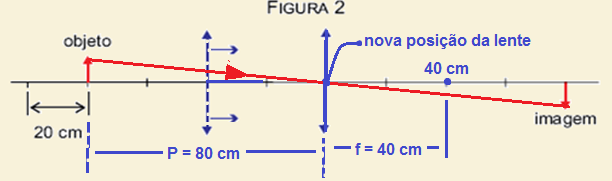
“ Todo raio de luz que incide passando pelo centro óptico da lente não sofre desvio”.
Na figura acima esse raio corta o eixo principal, localizando a lente num ponto à distância P = 80 cm do objeto.
05-
b) Que quantidade de água, a 95oC, deve ser colocada no calorímetro para que a temperatura final volte a ser de 80oC?
b) Agora você tem no calorímetro o bloco de concreto a 70oC e a água também a 70oC que vão trocar calor com a massa m de água a 95oC até que, no final, todos vão ficar com a mesma temperatura (de equilíbrio térmico) de te’=80oC.
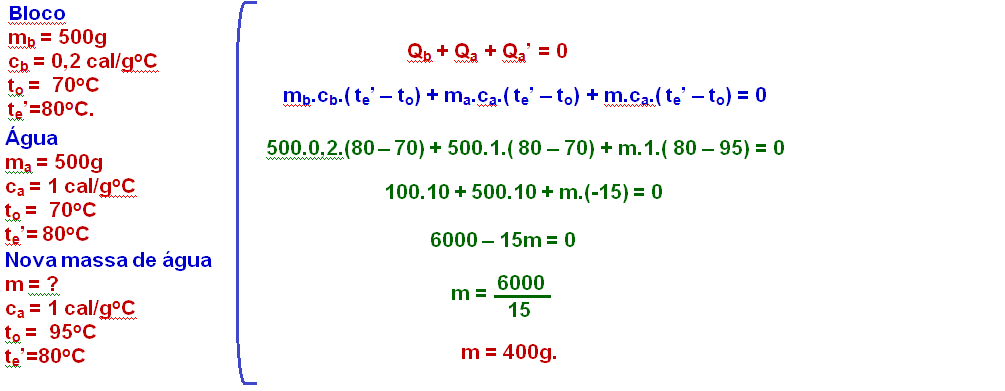
06- a) Esquematize o circuito elétrico que deve ser montado pelo eletricista (não é necessário desenhar todas as lâmpadas).
Indique quantas lâmpadas há em cada grupo e como são associadas. Indique também como os grupos são associados para serem ligados à rede elétrica.
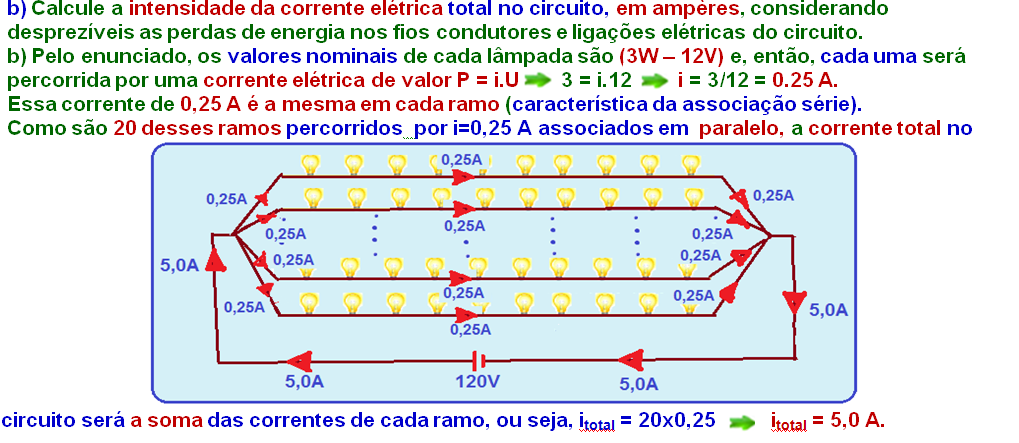
a) Na associação série a corrente elétrica i é a mesma para cada lâmpada e a tensão (ddp ou voltagem) Utotal = 120V é a soma das tensões nominais de cada lâmpada que deve ser de U=12V para que cada uma funcione normalmente.
Assim, você deve ter n = 120/12=10 lâmpadas associadas em série e funcionando normalmente em
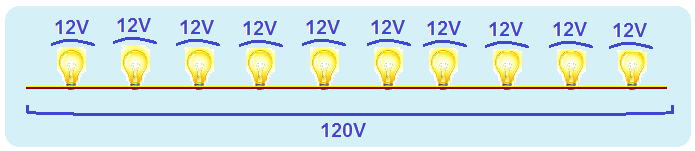
um único ramo e ligadas em Utotal =120V.
Acontece que você deve associar 200 lâmpadas e, então você deve ter uma associação paralelo de 20 ramos (20×10=200 lâmpadas), pois a característica dessa associação é que, nela cada ramo possui tensão de 120 V.
Esquema do circuito:
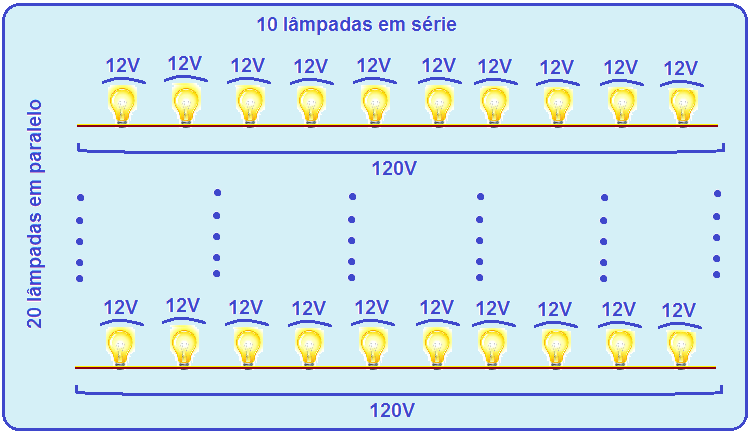
Os 20 ramos de 10 lâmpadas em série devem ser associados em paralelo e ligados na tomada de 120V.
07-
08-
09- Terceira lei de Kepler (lei dos períodos)
“ Os quadrados dos períodos T de revolução dos planetas (tempo que demora para efetuar uma volta completa em torno do Sol) são proporcionais aos cubos das suas distâncias médias R ao Sol”
T2/R3=constante=K’
O mesmo é válido para Terra-Lua. Se a distância média R da Lua à Terra aumenta, e ela é proporcional ao período de translação da Lua ao redor da Terra, esteperíodo também deve aumentar.
R- D
10-
11- Se uma placa metálica com orifício for aquecida, verifica-se que o orifício aumenta, como se
fosse constituído pelo material da placa, pois tudo se passa como se o furo tivesse um coeficiente de dilatação superficial igual àquele da substância da placa.
Como o exercício se refere aos raios você pode trabalhar com a dilatação linear.
Dilatação do raio externo R para a arruela de coeficiente de dilatação α para a variação de temperatura Δθ — ΔR = R.α.Δθ (I)
Dilatação do raio interno r para a arruela de coeficiente de dilatação α para a variação de temperatura
Δθ — Δr = r.α.Δθ (II)
(II)/(I) — Δr/ΔR = r.α.Δθ/ R.α.Δθ — Δr = (r/R).ΔR.
R- C
12- Ressonância
Qualquer sistema físico possui uma ou mais freqüências naturais de vibração. Quando ele é “excitado” por algum agente externo, agindo no ritmo de uma dessas freqüências, surge o fenômeno da ressonância, ou seja, ele começa a oscilar gradativamente até atingir uma dessas freqüências, onde sua amplitude é máxima.
Exemplos:
– Uma criança, num balanço já em movimento, sabe qual é o momento certo, para que, com o
movimento do corpo provoque um impulso, que faz aumentar a amplitude do movimento, obtendo assim, a ressonância. Trata-se de ressonância mecânica.
– Ao sintonizar uma emissora de rádio ou TV estamos fazendo com que nosso aparelho receptor entre em ressonância com a mesma freqüência que a das ondas eletromagnéticas da estação que as emitiu. Trata-se de ressonância eletrônica.
– As vibrações da corda de um violão entram em ressonância com o ar contido em sua caixa de
madeira “caixa de ressonância” ou com o a nota emitida por um diapasão, que vibram com a mesma freqüência da nota emitida pelo diapasão, afinando a corda do mesmo. Trata-se de ressonância sonora.
R- A
13- Lei de Snell-Descartes:
A relação entre o seno do ângulo de incidência e o seno do ângulo de refração é uma grandeza constante denominada índice de refração do segundo meio em relação ao primeiro, ou seja, seni/senr=n2/n1
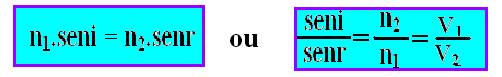
As expressões acima nos mostram que quando a luz passar de um meio menos refringente (menor indice de refração) para um meio mais refringente (maior índice de refração), o ângulo de refração será menor que o ângulo de incidência (ele se aproxima da normal) e menor será a velocidade da luz nele. (figura abaixo)
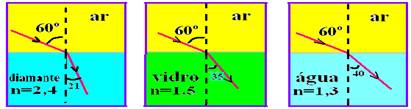
Pelo princípio da reversibilidade (caminho inverso), quando a luz passa de um meio mais refringente (maior índice de refração) para um menos refringente (menor índice de refração) ângulo de refração será maior que o ângulo de incidência.
Como o enunciado quer o maior ângulo de refração, o raio de luz deve passar do meio de maior índice do líquido (benzeno 1,50) para o meio de menor índice do vidro (crown 1,52).
R- E
14- Trabalho da força elétrica para levar o elétron de carga q=1,6.10-19C, da placa aceleradora A de
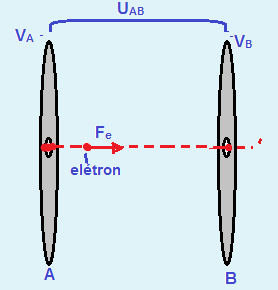
potencial VA até a B, de potencial VB, cuja diferença de potencial é UAB — WAB = q.UAB —
WAB= 1,6.10-19.UAB (I).
Utilizando o teorema da variação da energia cinética entre as placas A e B onde, a velocidade do
elétron de massa m = 9,1.10-31kg em A é nula (velocidade desprezível vA=0) e em B é vB = 4.107m/s.
WAB = EcB – EcA = mvB2 /2 – mvA2/2 = 9,1.10-31.(4.107)2/2 – 9,1.10-31.02/2 = 9,1.10-31.16.1014/2 – 0 —
WAB = 145,6.10-17/2 — WAB = 72,8.10-17 J (II).
(I) em (II) — 1,6.10-19UAB = 72,8.10-17 — UAB = 45,5.102 = 4,55.103 V.
R- E
15- Quando um solenóide é percorrido por corrente elétrica, a configuração de suas linhas de indução é obtida pela reunião das configurações de cada espira o que equivale à configuração das linhas de indução de um imã natural.
O sentido das linhas de indução no solenóide é fornecido pela regra da mão direita aplicada em uma
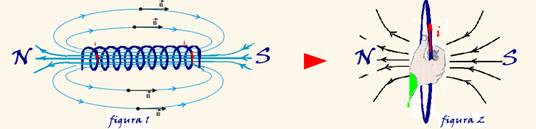
de suas espiras (figura 2) e em seu interior o campo magnético é praticamente uniforme (figura 1) e fora são linhas que saem do pólo norte e chegam ao pólo sul.
As linhas de força do campo magnético produzido por um solenóide são idênticas aos do campo magnético produzido por um imã.
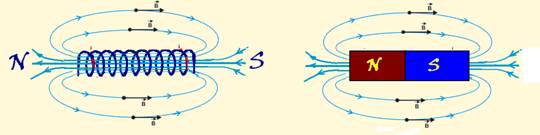
Na prática, é indiferente produzir-se um campo magnético por um ímã ou por um solenóide.
Observe nas figuras abaixo que, como a corrente elétrica sai do polo positivo da bateria, utilizando
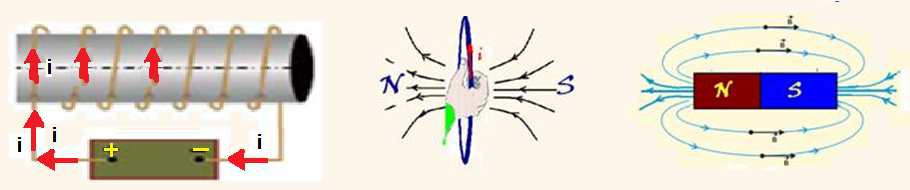
a regra da mão direita, os pólos do imã terão a distribuição da figura da direita.
R- C