RESOLUÇÕES
01- Reflexão total:
Fazendo a luz se refratar da água (mais refringente, maior índice de refração) para o ar (menos refringente, menor índice de refração), veja o que ocorre na sequência das figuras abaixo:
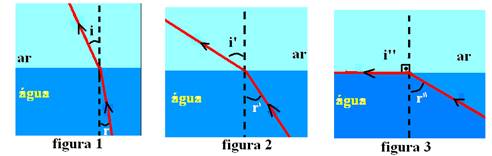
Verifique na figura 3 que, quando a luz incide na superfície da água com ângulo r’’, ela se refrata no ar praticamente paralelo à superfície da água (emergência rasante). Nesse caso específico, denominamos r’’ de ângulo limite L.
A partir daí começa o que denominamos de reflexão total.
I II
Para qualquer ângulo de incidência maior que o ângulo limite L ( i > L), o raio de luz sofre reflexão total ou reflexão interna retornando à água tal que i ≥ r.
Condições para que ocorra reflexão total:
1a – A luz deve se propagar do meio mais refringente (maior índice) para o meio menos refringente (menor índice)
2a – A luz deve incidir com ângulo sempre maior que o ângulo limite L.
Comparando essas duas condições com as afirmativas do exercício:
(I) O feixe luminoso propaga-se do meio menos refringente para o meio mais refringente. (Falsa)
(II) Para que ela ocorra, o ângulo de incidência α deve ser inferior ao ângulo limite da superfície de separação entre o núcleo e a casca. (Falsa)
(III) O ângulo limite da superfície de separação entre o núcleo e a casca depende do índice de refração do núcleo e da casca. (Correta)
(IV) O feixe luminoso não sofre refração na superfície de separação entre o núcleo e a casca.(Correta)
R- B
02- Teorema de Stevin:
A pressão no interior de um líquido em equilíbrio hidrostático é fornecida por P=Patm + dlíquido.g.h e é chamada de pressão total, pressão absoluta ou simplesmente pressão.
Observe na expressão do Teorema de Stevin P=Patm + dlíquido.g.h que a pressão P exercida por uma coluna líquida não depende das dimensões do recipiente que a contém, mas apenas da natureza do líquido, fornecida pela sua densidade (d), do local (g) e da altura da coluna (h).
Uma das conseqüências do teorema de Stevin é de que todos os pontos de uma superfície horizontal (a uma mesma altura h) suportam a mesma pressão, desde que o líquido seja o mesmo.
Uma das utilidades práticas dessa conseqüência são os vasos comunicantes, onde um mesmo
líquido que está em recipientes de formatos e volumes diferentes, interligados entre si, ficam sempre na mesma altura, pois suportam a mesma pressão
R- A
03-
04-
05-
Um sistema de corpos rígidos (no caso, os três fios), pode ser estudado pelo centro de massa desse sistema. Para isso, você pode admitir que toda a massa do sistema, esteja concentrada no centro de massa (no nosso caso, o ponto P) e que nele estejam aplicadas todas as forças externas (no caso, as forças magnéticas) (figura 2 abaixo).
Veja a sequência:
06- Observe na figura abaixo que a parcela do peso P que é transmitida até o ponto B da barra vale
FB=P/8.
Cálculo do momento de cada força com o polo em A e estabelecendo o sentido horário de rotação como positivo e o anti-horário como negativo
07-
08- Sendo o voltímetro ideal ele possui resistência interna infinita (isolante), por ele não circula corrente elétrica, então você pode retirá-lo do circuito, que fica conforme a figura abaixo:
Na sequência a seguir está sendo calculada a resistência elétrica do resistor equivalente:
Veja na figura abaixo que a corrente elétrica que circula pelo amperímetro (indicação do mesmo) é de 2,5A e veja também as correntes que circulam por cada resistor:
A diferença de potencial (tensão, voltagem) entre A e B é fornecida por UAB=R.i=0,3.1,25=0,375V.
A diferença de potencial (tensão, voltagem) entre A e C é fornecida por UAC=R.i=0,6.1,25=0,75V.
UAB = VA – VB VA – VB = 0,375V UAC = VA – VC VA – VC = 0,75V.
UAC – UAB = 0,75 – 0,375 = 0,375V (VA – VC) – (VA – VB) = 0,375 = VA – VC – VA + VB VB – VC =
0,375V.
Observe na figura que o voltímetro está inserido entre os pontos B e C então ele indicará a ddp entre esses dois pontos, ou seja, indicará UBC=0,375V.
R- A
09- Sendo a escada de material homogêneo seu peso
Na figura abaixo estão localizadas todas as forças que agem sobre a escada, seu peso
10- Pêndulo Simples – consta de uma massa m, presa na extremidade inferior de um fio ideal, fixada verticalmente na sua extremidade superior (figura)
Se o pêndulo simples oscilar, com oscilações de pequena abertura (no máximo 15o), ele descreve um movimento circular de raio R=L, sendo L o comprimento do fio.
Seu período (T), que é o tempo que ele demora para efetuar um “vai e vem” completo é fornecido pela expressão:
onde g é a aceleração da gravidade local.
R- C