Resoluções Dinâmica – 2014 – 2013

RESOLUÇÕES – 2014 – 2013

 As três leis de Newton

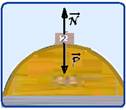
01- Se ele está com velocidade constante, independente da inclinação, ele está em MRU na vertical e na horizontale, pelo princípio da inércia, a resultante das forças que agem sobre ele é nula (equilíbrio dinâmico) — R- D

02- A força resultante sobre o bloco na direção do movimento é a força de atrito F_at=μN=μP= μmg= 0,4.m.10 — F_at=4m — segunda lei de Newton — F_R=F_at=ma — 4m=ma — a=4m/s² — Torricelli — V²=V_o² + 2.a.d — 0² = 20² + 2.(-4)d — d=400/8 —d=50m.

R- E

03- Como ele se move com velocidade constante na mesma altitude, na horizontal ele está em equilíbrio dinâmico (MRU) e, assim a força resultante na horizontal é nula (as forças horizontais se anulam).

Como ele permanece na mesma altitude (não sobe nem desce) a força resultante na vertical é nula (as forças verticais se anulam).

R- C

04- Desprezando-se a resistência do ar, qualquer corpo que estiver no espaço após lançamento

verical, lançamento oblíquo,queda livre, etc, terá como força resultante a força peso que tem sempre direção vertival e sentido para baixo.

R- A

05- Na vertical: Como cada dobradiça sustenta o peso do portão P=800N (vertical e para baixo) e cada uma suporta metade desse peso, cada dobradiça receberá uma força vertical e para cima de P’=800/2

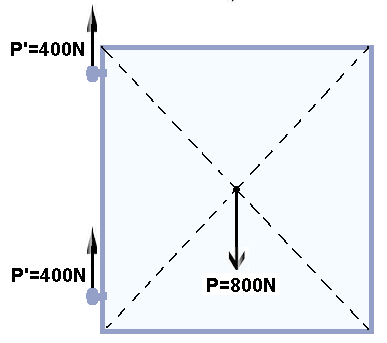
— P’=400N (figura acima). Assim, na vertical o portão está em equilíbrio, pois 2P’=P.

Na horizontal: na dobradiça superior deve surgir uma força horizontal e para a esquerda  impedindo que o portão gire no sentido horário e na inferior uma força horizontal e para a direita 

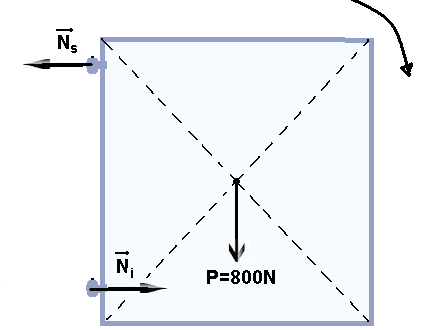
também impedindo que ele gire no sentido horário (figura acima).

Colocando o polo 0 (eixo de rotação) na dobradiça inferior vamos calcular o momento de cada força em relação a 0, estabelecendo o sentido horário de rotação como positivo:

M_Ns= – N_s.d= – N_s.1,6 — M_NS= – 1,6N_s

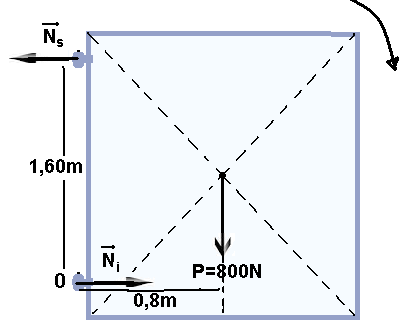
M_P= + P.d= + 800.0,8 — M_P= + 640 N.m

M_ni= N_i.d=N_i.0 — M_Ni=0

No equilíbrio de rotação a soma dos momentos de cada força deve ser nula:

– 1,6N_s + 640 = 0 — N_s=640/1,6 — N_s=400N — como na horizontal as forças devem se anular para que haja equilíbrio, N_s=N_i=400N.

R- C

06- Observe na sequência da figura abaixo que a força aplicada no tubo 1 tem direção paralela a do tubo 2 formando também um ângulo de 60^o com a horizontal e, como não existe atrito essa força 

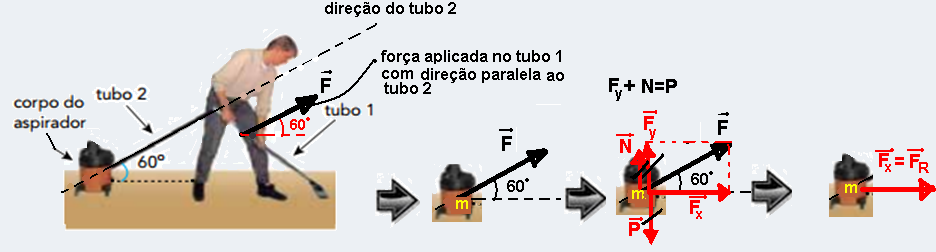
é transmitida até ao aspirador formando um ângulo de 60^o com a horizontal.

Essa força foi decomposta em duas parcelas F_x=Fcos60^o=4.0,5=2N e em . Como o aspirador não se move na vertical a força peso  anula as forças  e a normal . Assim, a única força responsável pelo movimento do aspirador é F_x=2N que é a força resultante sobre o mesmo.

Aplicando a segunda lei de Newton F_R=F_x=ma — 2=2.a — a=1m/s²

R- B

07-

Observe a análise de cada trecho:

Resumindo:

R- E

08- Pelo enunciado — F_E=2F_D — durante o movimento com aceleração de a=0,2m/s² a força de atrito F_at =240N e é constante.

Aplicando a segunda lei de Newton — F_R=ma — F_D + F_E – F_at = ma — F_D + 2F_D – F_at = ma —

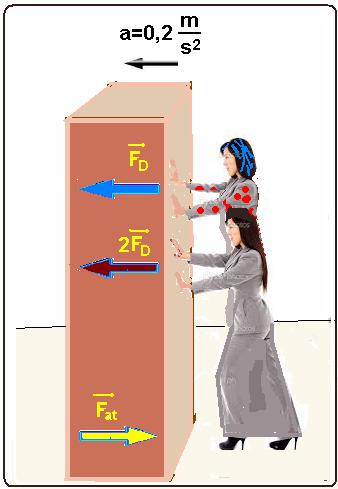
3F_D – F_at =ma — 3F_D – 240 = 120.0,2 — F_D = (24 + 240)/3 — F_D=88N.

F_E=2F_D=2.88=176N.

R- D

09- Peso do paciente — P=m.g=50.10=500N — parcela horizontal da tração — T_x=Tcos30^o=T√3/2 — T_x=0,87T.

Observe na figura que ele não deve se deslocar horizontalmente então a força de atrito deve anular a parcela horizontal da tração — F_at=μN=μP=0,26.500 — F_at=130N — F_at = T_x — 130 = 0,87T — T=

130/0,87 — T=148,5N.

Até T=149,5N e m=14,95kg ele não se desloca e assim, a massa máxima deve ser de m=13kg.

R- B

10- A força resultante na direção do movimento é a força de atrito, constante, contrária ao mesmo que produz uma aceleração de retardamento também constante de intensidade F_R=F_at=ma — V=V_o – at — função de primeiro grau (reta decrescente), velocidade diminuindo até parar, quando V=0.

R- B

11- Se você não domina a teoria, ela está detalhada a seguir:

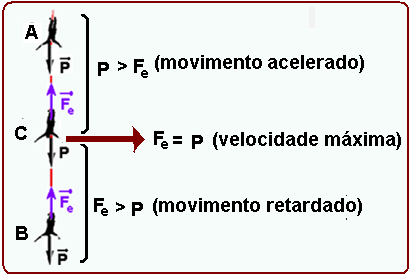
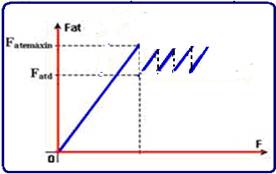
Força de atrito estático () e força de atrito dinâmico().

Considere um bloco de massa m sujeito a uma força externa de intensidade variável

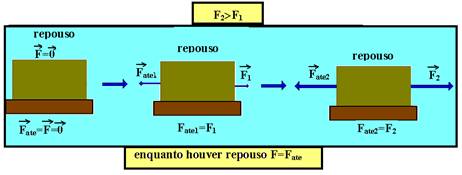
Quando o corpo estiver em repouso e não houver força externa, F_at=0.  Com o corpo permanecendo em repouso, aumentando F, a intensidade da força de atrito estático também aumenta (figuras acima), até que o corpo fique na iminência de movimento (figura abaixo).

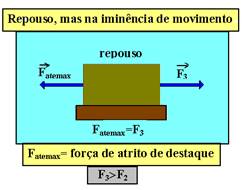
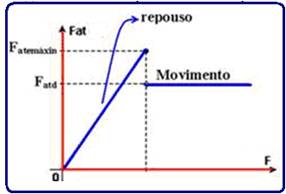
Quando o corpo está na iminência de movimento a intensidade da força de atrito estático é máxima. Uma força de intensidade maior que F₃ faz com que o corpo entre em movimento e, a partir daí a força de atrito é dinâmica ou cinética.

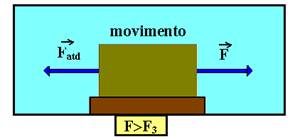
Depois que o bloco entra em movimento a força de atrito é denominada força de atrito dinâmica, e é sempre a mesma,  independente da velocidade A intensidade da força de atrito dinâmica é ligeiramente menor que a intensidade da força de atrito estática máxima.

Suponha, nos exemplos acima, que se F₁ tiver intensidade de 3N, F_at1 também terá intensidade de 3N e o corpo continua em repouso.. Se F₂=5N, F_at2=5N e o corpo continua em repouso. Se F₃=7N, a máxima intensidade de atrito estático, que corresponde à iminência de movimento, é dada por:

F_ate=m_e.N

Onde, F_ate é força de atrito estático máximo ou simplesmente força de atrito estático, m_eé coeficiente de atrito estático e N a intensidade da força normal, que o bloco troca com o plano.

Portanto o bloco só entrará em movimento com qualquer força que seja maior que 7N. Assim, se aplicarmos por exemplo, 8N o bloco entrará em movimento e agora a força de atrito será dinâmica e dada por:

F_atd=m_d.N

Onde, F_atd é força de atrito dinâmico, m_d é coeficiente de atrito dinâmico e N a intensidade da força normal, que o bloco troca com o plano.

Verifica-se experimentalmente que F_ate>F_atd e que m_e>m_d.

O gráfico abaixo representa todo o processo explicado acima.

 

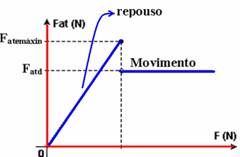
R- B

12- Na figura 1 foram colocados os módulos de todas as forças que agem sobre cada bloco — P_A. P_B e P_C que correspondem aos pesos de cada bloco — F_el – força elástica aplicada pela mola sobre os blocos C e B — Fat – força de atrito sobre o bloco B, contrária ao movimento — T – força de tração trocada entre os blocos A e B — P_NB – parcela do peso perpendicular ao plano inclinado que o comprime contra o mesmo — P_PB – parcela do peso paralela ao plano responsável pela descida do bloco — a – aceleração de cada bloco no sentido horário — na figura 2 foram colocadas apenas as forças que agem na direção do movimento de cada bloco:

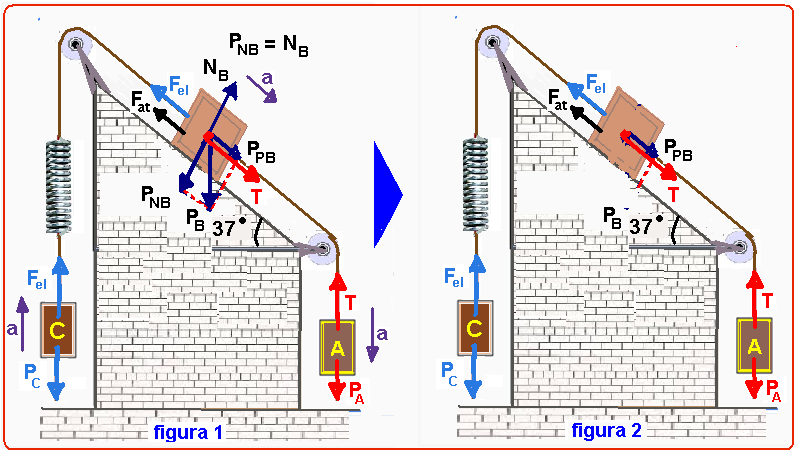
P_pB=Psen37^o=mgsen37^o=m_B.10.0,6=6m_B.

F_at=μ.N_B= μP_NB= μm_B.10.cos37^o=0,4.m_B.10.0,8=3,2m_B.

F_el=k.x=1240.0,02=24,8.

F_R=m_b.a — T + P_pB – (F_el + F_at) = m_B.a — 22,8 + 6m_B – 24,8 – 3,2m_B = m_B.2,4 — 6m_B – 5,6m_B = 2 — m_B=2/0,4 — m_B=5kg.

R- E.

13- Princípio da Inércia (Primeira Lei de Newton)

“Todo corpo que esteja em repouso ou em movimento retilíneo e uniforme (movendo-se em trajetória reta com velocidade  vetorial constante), tende a continuar nestes estados se a força resultante que age sobre ele for nula”.

R- A

Forças no MCU

01- Cada garota encontra-se em movimento circular uniforme com a mesma velocidade angular (W), pois “varrem” o mesmo ângulo no mesmo tempo — em todo movimento circular surge sempre uma força resultante denominada força resultante centrípeta  com as seguintes características:

Essa força resultante centrípeta sobre a garota 1 tem intensidade F_c1=T₁=m.W².2R — T₁=2mW²R (I) e

sobre a garota 2 — F_c2=T₂ – T₁=mW²R — T₂ – T₁= mW²R (II) — veja figuras abaixo:

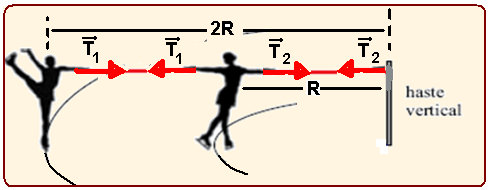
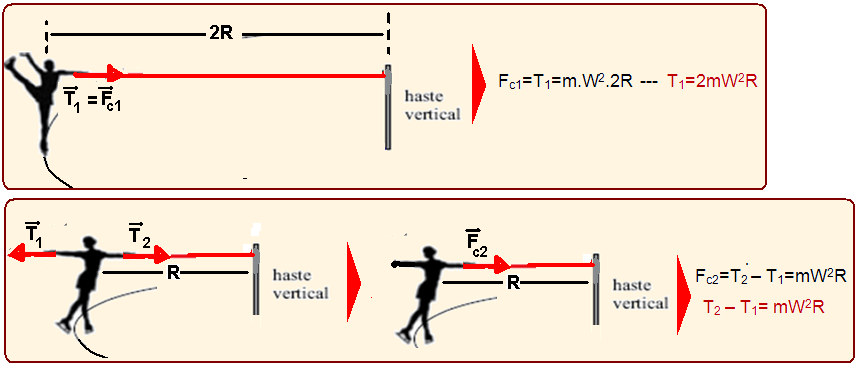
substituindo (I) em (II) — T₂ – 2mW²R = mW²R — T₂=3mW²R e T₁=2mW²R (I) — dados — T₁=120N —120=2mw²R —mw²R=120/20=60 — T₂=3.60 — T₂=180N — R- E.

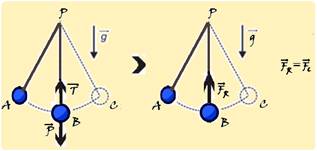
02- Na direção radial— o exercício afirma quea pessoa se solta do cipó no instante em que sua velocidade fica novamente igual a zero, ponto S da figura — se nesse ponto a velocidade é nula V_S=0, nele a força resultante centrípeta também é nula, pois F_CS=m.(V_S)²/2=m.0²/2=0 — F_CS=0 — então a aceleração

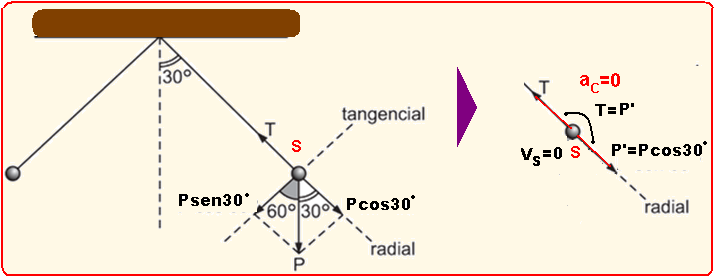
centrípeta em S será também nula, pois F_C=m.a_C=0 — a_C=0 e isso ocorre porque a tensão T anula a componente oposta do peso P’=Pcos30^o 

 Na direção tangencial— a força resultanteF_R sobre o corpo em S (responsável pelo movimento na

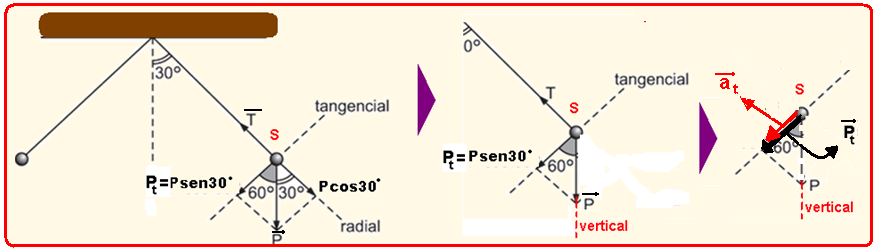
direçãoperpendicular ao cipó) é a parcela tangencial do peso P_t=Psen30^o — F_R=ma — F_R=P_t —

ma=mgsen30 — a=gsen30^o=10.(1/2) — a_t=5m/s²— essa aceleração é a tangencial e forma um ângulo de 60^o com a vertical —R- E

03- Para ir de A até B o motociclista percorre meio arco de circunferência de raio R, ou seja, percorre ΔS=2πR/2— ΔS=πR — sua menor velocidade média será V=ΔS/Δt, onde Δt é o intervalo de tempo que ele demora para percorrer ΔS — V=πR/Δt— note que essa é velocidade média e, portanto, é a mesma em A e em B — Δt=πR/V (I) — sendo o objeto abandonado (V_o=0) em A ele cai em queda livre com aceleração igual à da gravidade g, percorrendo a distância vertical 2R=ΔS — equação horária do espaço de uma queda livre — ΔS=V_o.Δt + g.(Δt)²/2 — 2R=0 + g.(Δt)²/2 (II) — observe que o tempo que o objeto demora para chegar em B em queda livre, é o mesmo que o motociclista demorou também para chegar em B e, assim, você pode substituir (I) em (II) — 2R=g.(πR/V)²/2 — 4R=g.(πR/V)² — 4R=g.π².R²/V² — 4=g.π².R/V² — 4V²=g.π².R — V²= g.π².R/4 (III) — mas, no ponto A as forças que agem sobre o motociclista são seu peso P (vertical e para baixo) e a força normal N que ele troca com a superfície superior do globo

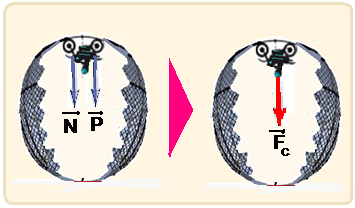
(também vertical e para baixo)— em todo movimento circular existe sempre uma força resultante centrípeta dirigida para o centro da circunferência, de intensidade F_c=m.V²/R — no ponto A F_c=P + N — mV²/R=N + P (IV) — substituindo (III) em (IV) — m.(g.π².R/4)/R=N + P — m. g.π²/4=N + P — mg=P — P.π²/4=N + P — π²=10 —

10P/4=N + P — 2,5P=N + P — 2,5P – P=N — 1,5P=N — N/P=1,5.

04- a) Energia mecânica no ponto I — E_mI=mgh + mV²/2= mgh + m0²/2 — E_mI=mgh

Energia mecânica no ponto II — E_mII= mgh + mV²/2= mg0 + mV²/2 — E_mII=mV²/2

Pelo teorema da conservação da energia mecânica — E_mI=E_mII — mgh=mV²/2 — V=√(2gh)

b) No ponto II as forças que agem sobre o corpo são seu peso (vertical e para baixo) e força de tração no fio (vertical e para cima) — em todo corpo em movimento circular surge uma força

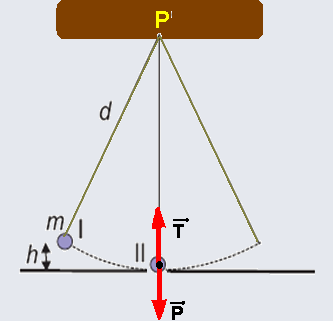
resultante centrípeta de direção radial, dirigida para o centro da circunferência (no caso, para cima) e de intensidade F_c=mV²/R=mV²/d — mas, F_c=T – P — mV²/d = T – mg — m.(√(2gh)² /d = T – mg —

m.2gh/d = T – mg — T=mg + 2mgh/d — T=mg(1 + 2h/d)

Trabalho- Energia

01- Como o entulho de massa m está descendo com velocidade constante ele está em MR( (equilíbrio dinâmico) e a força resultante sobre ele deve ser nula e, para que isso ocorra, a intensidade da força

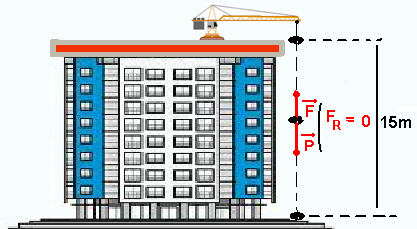
aplicada pelo guindaste deve ser igual ao peso do entulho — F=P=mg=m.10 — P=F=10m.

Cálculo do trabalho realizado pela força F=P — W=F.d.cosα=10m.15.cos0^o — W=150.m.

R- D

02- Pela tabela periódica, você tem que as massas dos isótopos do chumbo (Pb), da prata (Ag), do hélio (He) e do hidrogênio (H), são respectivamente: 207,2, 107,8, 4,002 e 1,008. 
Assim, m_Pb > m_Ag > m_He > m_H
Pela expressão da energia cinética E_c=mV²/2 você verifica que, sendo a velocidade a mesma para os 4 feixes de átomos, aenergia cinética é diretamente proporcional à massa. Assim, a relação pedida é: E_Pb > E_Ag > E_He > E_H

R- D

03- A energia armazenada por um corpo de massa m devido ao fato de ele se encontrar a certa altura h recebe o nome de energia potencial gravitacional (E_p), de expressão matemática:

onde:

E_p  —  energia potencial gravitacional – no SI, medida em joules (J)

m  —  massa – no SI, medida em quilograma (kg)

g  —  aceleração da gravidade local – no SI, medida em m/s² ou N/kg

O segundo trecho do passeio corresponde à ida do bondinho de massa m=5000kg do Morro da Urca (h_U=220m) ao Pão de Açúcar (h_P=400m) — energia potencial gravitacional do bondinho no Morro da

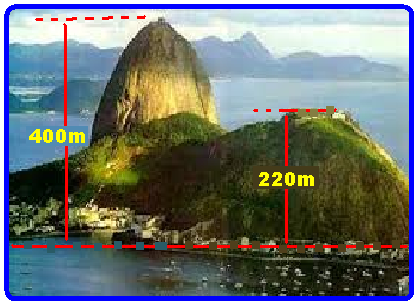
Urca,em relação ao solo — E_pU=m.g.h_U=5000x10x220=11000000=11.10⁶ J — — energia potencial gravitacional do bondinho no Pão de Açúcar, em relação ao solo — E_pP= m.g.h_P=5000x10x400=

20000000=20.10⁶ J — variação de energia potencial gravitacional pedida — ΔE_p=20.10⁶ – 11.10⁶=

9.10⁶ J — R- A

04- Cálculo do trabalho da força de atrito (F_at), contrária ao deslocamento, e de intensidade fornecida F_at=380N num deslocamento de ΔS=d=72km=72.10³m — W_Fat=F_at.d.cos180^o=380.72.10³.(-1) —

W_Fat= – 27 360.10³ J = – 2,736.10⁷J — em módulo — |W_Fat|= 2,736.10⁷J (energia dissipada devido ao atrito com o ar)

05- No instante do salto o atleta tem duas velocidades, uma horizontal de intensidade V_h=10m/s e outra, vertical de intensidade V_vque produz uma energia cinética de E_c=70% de uma energia de E=500J, ou seja, produz uma E_c vertical de E_Cv=(70/100)x500=0,7×500 — E_Cv=350J — essa energia cinética origina uma velocidade vertical de E_Cv=mV_v²/2 — 350=70.V_v²/2 — 70V_v²=2×350 — V_v²=700/70 — V_v=√(10) m/s —

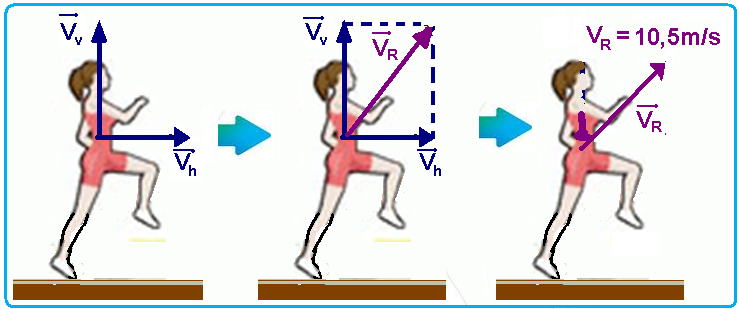
então, no instante do salto você tem duas velocidades — uma horizontal de intensidade fornecida V_h=10m/s e outra vertical de intensidade V_v=√(10)m/s — a velocidade pedida, velocidade resultante, no momento do salto corresponde à soma vetorial dessas duas velocidades — aplicando Pitágoras — V_R²=V_h² + V_v²= 10² + (√10)²=100 + 10— V_R=√(110)≈10,488m/s — R- B

06-

R- E

07- Força resultante sobre o automóvel pela segunda lei de Newton — F_R=m.a=1500x(1/12) — F_R=125N

trabalho da força resultante no deslocamento de d=1350m — W=F_R.d=125×1350 — W=168 750J W=1,678.10⁵J — R- D

08- Trata-se de um sistema dissipativo que surge quando o trabalho é realizado por forças dissipativas(força de atrito, força de resistência do ar, etc.) no qual, parte da energia mecânica do sistema é dissipada nas formas de energia térmica, sonora, etc. Assim a energia mecânica do sistema, diminui e, nesse caso, o trabalho das forças não conservativas W (força de atrito, força de resistência do ar, etc.) é igual à  energia total dissipada, ou seja, é igual à variação da energia mecânica —E_{mecanicafinal} – E_{mecanicainicial}=W_{forçasdissipativas}.

 Inicialmente você pode calcular a distância ∆S percorrida pelo bloco entre os pontos A e B pela área do gráfico Vxt fornecido (figura 2) — área do triângulo=AB=∆S=b.h/2=0,5×4/2=1m — cálculo da altura h entre os pontos A e B

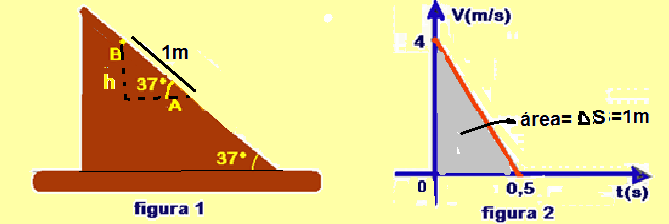
(figura 1) — sen37^o=cateto oposto/hipotenusa — 0,6=h/1 — h=0,6m — para a subida — W_{forçasdissipativas=}E_{mecanicafinal} – E_{mecanicainicial} — W_fat=E_mA – E_mB — veja pelo gráfico da figura 2 que a velocidade inicial em A é 4m/s e a em B é zero — E_mA=mgh_A + mV_A²/2=2.10.0 + 2.4²/2=0 + 16 — E_mA=16J — E_mB=mgh_B + mV_B²/2=2.10.0,6 + 2.0²/2 — E_mB=12J — W_fat=16 – 12=4J — esse trabalho é o mesmo tanto para a subida quanto para a descida — para a descida — —W_{forçasdissipativas=} E_{mecanicafinal} – E_{mecanicainicial} — W_fat=E_mB – E_mA — veja pelo gráfico da figura 2 que a velocidade inicial em A é 4m/s e a em B é zero — E_mA=mgh_A + mV_A²/2=2.10.0 + 2.V_A²/2 — E_mA=V_A² E_mB=mgh_B + mV_B²/2=2.10.0,6 + 2.0²/2 — E_mB=12J — W_fat=16 – 12=4J — esse trabalho é o mesmo tanto para a subida quanto para a descida — para a descida — W_fat=E_mB – E_mA — 4=12 – V_A² — V_A=√8=2√2m/s.

09- Energia mecânica no ponto A de onde o menino parte do repouso — E_mA=m.g.h — energia mecânica no ponto B de onde chega com V_B=2m/s — E_mB=mV_B²/2=m.4/2 — E_mB=2m — E_mA = E_mB

mgh = 2m — h=2/g=2/10 — h=0,2m.

Agora ele sai do ponto A com velocidade de V_A=1,5m/s — E_mA=mV_A²/2 + mgh=m.1,5²/2 + m.10.0,2 — E_mA= 1,125m + 2m —E_mA=2,125m — E_mB=mV_B²/2 — E_mA =E_mB — 2,125m = mV_B²/2 — V_B=√4,25 — V_B=2.06m/s.

R- C

10- O trabalho da força peso é negativo na subida, positivo na descida e nulo num deslocamento horizontal e fornecido por W=P.h ou W=m.g.h.

O trabalho da força peso entre dois pontos A e B, não depende da trajetória, mas apenas da altura

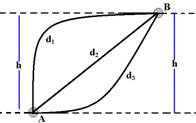
(h) vertical entre A e B e é fornecido por W_BA=+P.h na descida e por W_AB= -P.h na subida por qualquer trajetória (d₁, d₂ ou d₃).

No caso do exercício a altura h vale — sen30^o_­=h/8 — h=8.0,5=4m — módulo do trabalho do peso — W=P.h=20.4=80J.

R- C

Dinâmica Impulsiva

01-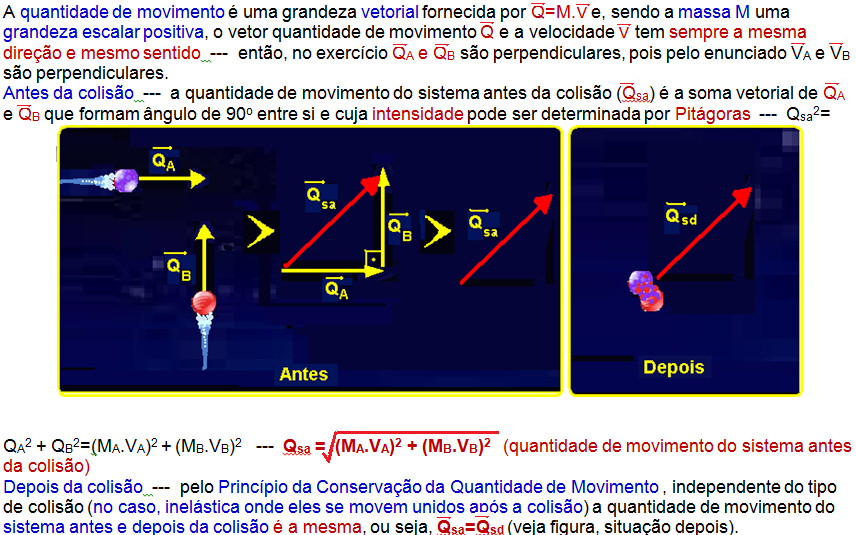 

R- B

02- Cálculo da velocidade V com que o sistema bloco + projétil inicia a compressão da mola pela conservação da quantidade de movimento.

Choque entre o projétil e o bloco:

M=180g=0,18kg — m=20g=0,02kg — V_p=200m/s — V=?

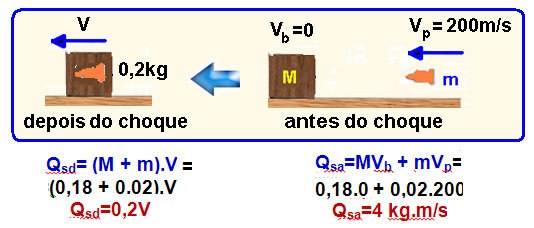
Pelo princípio da conservação da quantidade de movimento — Q_sa = Q_sd.

4 = 0,2V — V=4/0,2 — V=20m/s (velocidade com que o sistema (projétil + bloco) começa a comprimir a mola.

Agora vamos utilizar o teorema da conservação da energia mecânica no sistema (bloco-projétil) de massa M_s=(0,18 + 0,02)=0,2kg em duas situações:

* Energia mecânica de M_s imediatamente antes de começar a comprimir a mola onde a energia potencial elástica é nula (mola descomprimida) só possuindo energia cinética — E_mi=M_sV²/2= 0,2.(20)²/2 — E_mi=40J.

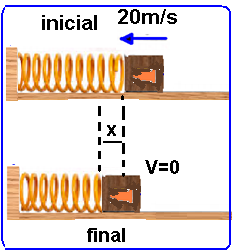
* Energia mecânica de M_s após a mola estar comprimida de x e M_s parado (V_s=0) onde a energia cinética é nula e o sistema só possui energia potencial elástica — E_mf=kx²/2=2.10³x²/2 — E_mf=10³x².

Sendo o sistema conservativo — E_mi = E_mf — 40 = 10³x² — x²=40/10³=4.10^-2 — x²=0,04 — x=0,2m

X=20cm.

R- D

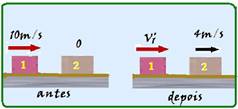
03- Depois de unidos, o carrinho com compras de massa 30kg e o vazio de massa 20kg se movem

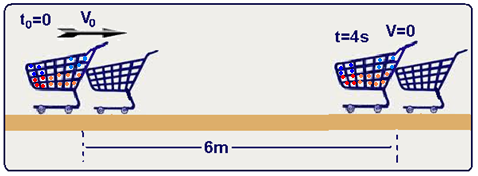
engatados, com massa total m=50kg, e com sua velocidade passando de V_o para V=0 (para), percorrendo ΔS=6m em t=4s.

Cálculo da velocidade V_o do conjunto:

Pelo enunciado, antes do acoplamento o carrinho de massa 30kg e velocidade V’ se move em direção ao carrinho de massa 20kg que estava parado e, imediatamente após o acoplamento ambos, de massa 50kg se movem unidos com velocidade V_o=3m/s. Aplicando o princípio da conservação da quantidade de movimento:

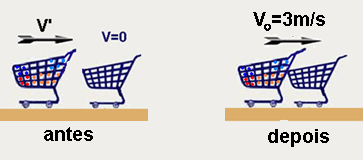
Antes — Q_sa=30V’ + 20.0 — Q_sa=30V’

Depois — Q_sd=(30 + 20).3 — Q_sd=150kgm/s

Q_sa = Q_sd — 30V’ = 150 — V’=5m/s

R- A

04- Como a massa M_ext do extintor não foi fornecida você deve avaliar uma massa que esteja dentro de um intervalo razoável, por exemplo, M_ext=20kg — você pode utilizar a conservação da quantidade de movimento para avaliar a velocidade pedida já que o extintor (sistema) está isolado — antes de lançar o jato de CO₂, o sistema está em repouso (V_antes=0) — depois que foi lançado a massa m=50g=0,05kg com velocidade de V_CO2=20m/s, o extintor de massa M_ext=20kg recua com velocidade V_ext tal que:

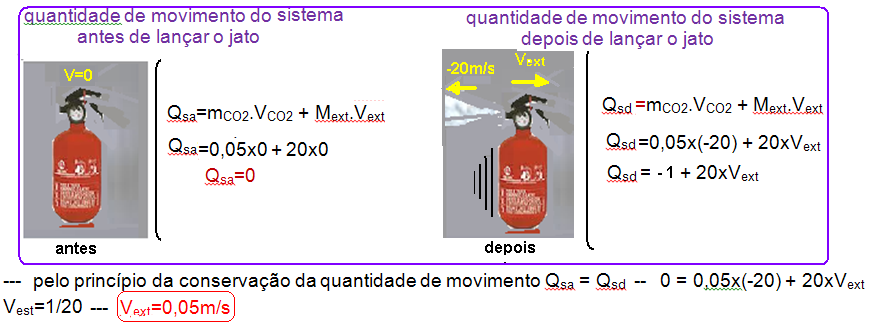
05- Em todo choque elástico (perfeitamente elástico) se os corpos possuirem a mesma massa eles trocam suas velocidades.

Após o choque a bola incidente para e a bola alvo segue com velocidade de 2m/s.

R- C

06- Estando o garoto em repouso dentro do barco, o sistema está em equilíbrio estático na vertical e a força resultante sobre ele é nula.

Forças verticais que agem sobre sistema (garoto mais barco) de massa m_s=50 + 150=200kg:

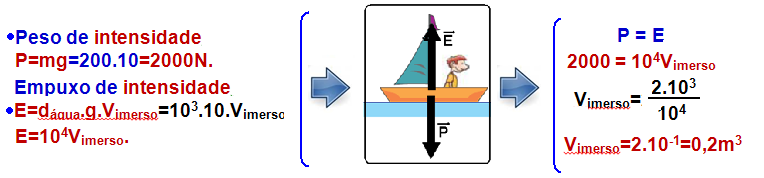
Agora você vai trabalhar na horizontal, utilizando o princípio da conservação da quantidade de movimento do sistema garoto-barco:

Antes do salto:

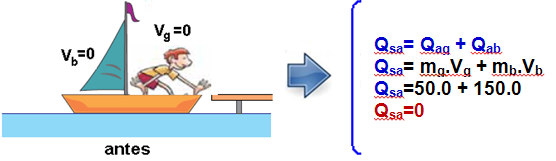
Depois do salto:

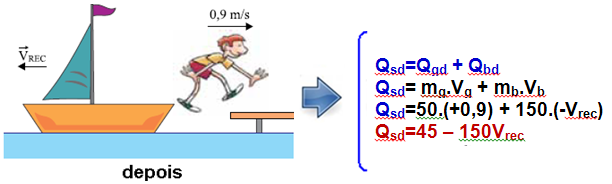
Pelo princípio da conservação da quantidade de movimento:

Q_sa = Q_sd — 0 = 45 – 150V_rec — V_rec=45/150 — V_rec=0,3m/s

07- Inicialmente você tem o núcleo de polônio inicialmente em repouso (V_Po=0) e, assim a quantidade de

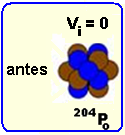
movimento inicial é nula pois, Q_i=mV_po=204u.0 — Q_i=0 — depois o núcleo de polônio se transforma em

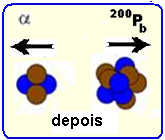
um núcleo de chumbo com velocidade de módulo V_Pb e em uma partícula alfa com velocidade de módulo V_α — a quantidade de movimento do sistema depois da transmutação será — Q_d=m_Pb.V_Pb + m_α.V_α=200u.V_P

+ 4u.V_α— pelo Princípio da Conservação da quantidade de movimento — Q_i=Q_d — 0 = 200u.V_P + 4u.V_α

4u.V_α = – 200uV_Pb — V_α = – 50 V_Pb­— energia cinética do núcleo de chumbo — E_Pb=m_Pb.V²_Pb/2 — E_Pb=200u.V²_Pb/2 (I) — energia cinética da partícula alfa — E_α=m_α.V²_α/2 — E_α=4u.(-50V_Pb)²/2 = 4ux 2500. V²_Pb/2— E_α =10000u.V²_Pb/2 (II) — (I)/(II) — E_Pb/E_α=(200u.V²_Pb/2)/(10000u.V²_Pb/2) — E_Pb/E_α =

(200u.V²_Pb/2)x(2/10000u.V²_Pb) — E_Pb/E_α =200/10000=1/50 — E_Pb=E_α/50 — R- C

08- a) Teorema do Impulso: “O impulso da força resultante de um sistema de forças que age sobre um corpo é igual à variação da quantidade de movimento do corpo“

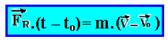
 Pelo enunciado, o módulo da velocidade da bola de massa m=300kg no ponto B, imediatamente antes de atingir a estrutura do prédio é de V_o=2m/s, o choque dura Δt=0,02s e após esse intervalo de tempo a bola para instantaneamente V=0 — aplicando o teorema do impulso:

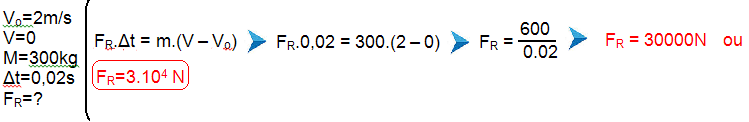
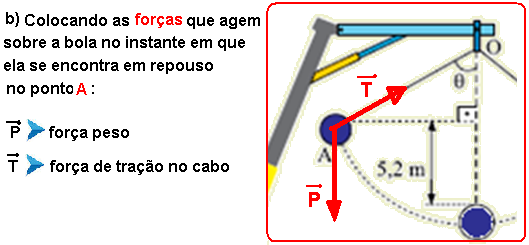
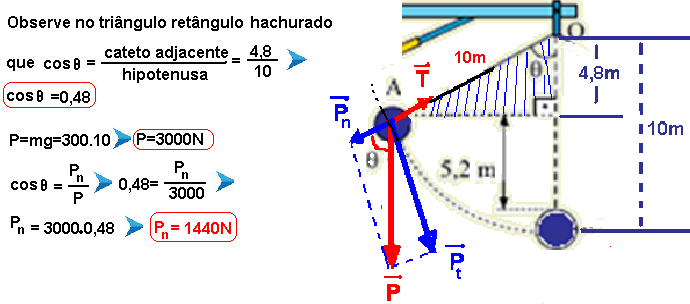
Se o enunciado afirma que no ponto A a velocidade da bola é nula, ele está afirmando que a força resultante centrípeta nesse ponto também é nula, pois F_c=mV²/R=m.0²/R=0 — para que isso ocorra, a intensidade da componente normal (radial) do peso P_n=1440N deve anular a força de tração no fio que é pedida, ou seja, F_n=T=1440N — observação: É a componente tangencial do peso P_t=Psenθ que faz a bola descer.

09- a) Observe que, nesse deslocamento de d=20cm=0,2m fornecido o exercício pede o trabalho da força de atrito  de intensidade F_at=μN=μP=μmg=0,4.3.10 — F_at=12N

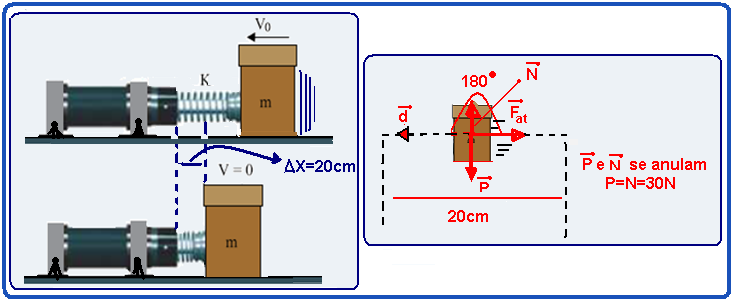
O trabalho da força de atrito W_Fat, onde F_at=12N, no deslocamento de d=0,2m e α=180^o é fornecido por

W_Fat=F_at.d.cosα=12.0,2.cos180^o=1,4x(-1) — W_Fat= – 2,4J

10- a) Cálculo da velocidade V_1i com que a partícula de massa M que partiu de P com velocidade V_p=0 e chega em que Q no início da pista horizontal, pela conservação da energia mecânica (figura 1):

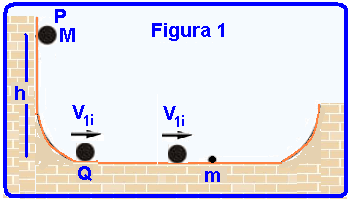
Energia mecânica em P — E_mP = MV²/2 + Mgh=M.0²/2 + M.10.1,25 — E_mP = 12,5M.

Energia mecânica em Q — E_mQ = MV_1i²/2 + Mgh= MV_1i²/2 + M.10.0 — E_mQ = MV_1i²/2

E_mP= E_mQ — 12,5M = MV_1i²/2 — V_1i=√25 — V_1i=5m/s — como não existe atrito é com essa velocidade com que ela chega até a partícula 2 imediatamente antes da colisão.

b) Observe na figura abaixo a situação antes da colisão e depois da colisão onde será calculada a quantidade de movimento do sistema antes e depois da colisão.

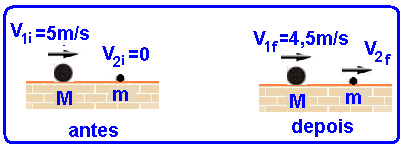
Antes — Q_sa=M.5 + m.0 — Q_sa=5M — depois — Q_sd=M.4,5 + m.V_2f — Q_sd=4,5M + V_2fm.

Q_sa = Q_sd — 5M = 4,5M + V_2fm — 0,5M = V_2fm — V_2f=0,5M/m.

Sendo a colisão elástica o coeficiente de restituição e é igual a 1 — e=módulo da velocidade relativa depois/módulo da velocidade relativa antes — 1 = V_2f – 4,5/5 – 0 — 5 = V_2f – 4,5 — V_2f = 9,5m/s.

Com essa velocidade inicial de V_i=9,5m/s a partícula m atinge a altura máxima em S onde V_S=0 —

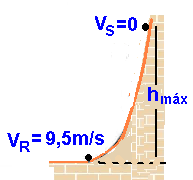
Energia mecânica em R — E_mR=m.(9,5)²/2 + m.10.0 — E_mR=45,125m (I). — energia mecânica em S — E_mS=m.0²/2 + m.10.h_max — E_mS=10mh_máx. (II).

Igualando (I) com (II) — 45,125m = 10mh_máx — h_máx=4,5125m

Primeira lei de Newton

29-  Princípio da Inércia (Primeira Lei de Newton)

“Todo corpo que esteja em repouso ou em movimento retilíneo e uniforme (movendo-se em trajetória reta com velocidade  vetorial constante), tende a continuar nestes estados se a força resultante que age sobre ele for nula”.

             

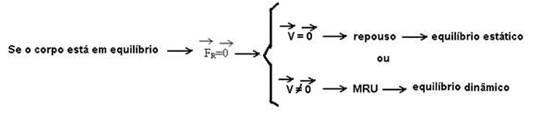
Quando a força resultante sobre ele for nula, se ele estiver em repouso, tende a continuar em repouso e se estiver em movimento com velocidade  tenderá a se mover em linha reta com velocidade . 

R- C.

30 – O momento de inércia refere-se a uma resistência à mudança no movimento rotacional de um corpo  —  é evidente que quanto mais próximo o centro massa do corpo estiver do eixo de rotação, menor será o momento de inércia, e quanto mais afastada a massa estiver do eixo de rotação, maior será seu momento de inércia  —  R- B.

31-  Isso ocorre porque você está na atmosfera que, por sua vez, por inércia, está acompanhando a Terra  —  isso se deve ao fato de existir uma força que atrai todos os corpos em direção ao centro da Terra chamada força gravitacional ou força peso  —  R- D.

 

Segunda lei de Newton

34- – a) Quando a caixa é arrastada com velocidade constante, pelo princípio da inércia a força resultante sobre ela é nula (equilíbrio dinâmico)  —  nesse caso, a intensidade da força aplicada pelo fio deve anular a força de atrito  —  F = F_at  —  F=1N.

b) Quando a intensidade da força aplicada pelo fio é maior que F=1N, a caixa entra em movimento acelerado, mas a força de atrito continua sendo de F_at=1N, pois, dentro de certos limites, independe da velocidade que, no caso, vai aumentando  —  pelo gráfico, a força (F) de tração no fio  é proporcional à aceleração (a)  —   quando, por exemplo, a aceleração for de 15m/s², a força será de 4N  —  a força resultante sobre a caixa vale  —  F_E=F – F_at=4 – 1=3N  — 

Princípio fundamental da Dinâmica  —  F_R=m.a  —  3=m.15  —  m=0,2 kg.

35-  Na figura abaixo as forças  foram projetadas na vertical e na horizontal  —  F_1x=F₁cosα  — 

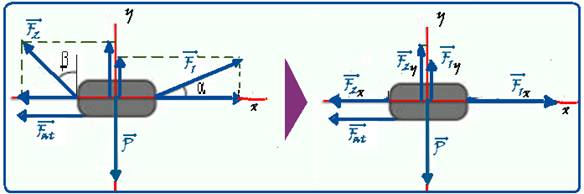
F_1y=F₁senα  —  F_2x=F₂senβ  —  F_2y=F₂cosβ.

01. Correta  —  supondo que o corpo se mova para a direita  —  R_x=F_1x – F_2x – F_at  —  R_x=F₁cosα – F₂senβ – μN.

02. Correta  —  .

04. Falsa  —  se a resultante do sistema for nula, o poderá estar em repouso(equilíbrio estático ou em movimento retilíneo e uniforme (princípio da inércia).

08. Falsa  —  se ele estiver subindo  —  R_y=F_1y + F_2y – P  —  R_y=F₁senα + F₂cosβ – P.

16. Falsa  —  como existe força de atrito, ele deve atuar no sistema.

R- (01 + 02)=03.

 

Terceira lei de Newton

20-  Entre os animais que desenvolveram o tipo de vôo pára-quedismo está o sapo voador de Bornéu, Rhacophorus dulitensis  —  o pára-quedas é formado através de membranas presentes nas patas  —  quando os animais descem das árvores, age uma força aerodinâmica paralela a direção do ar que passa por eles  —  essa força pode ser chamada de

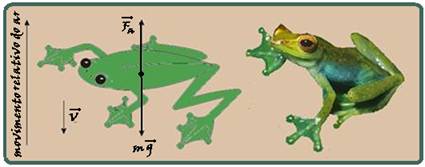
 força de resistência  —  o animal atinge uma velocidade constante quando esta força total contrabalancear o seu peso.

 O animal planador se desloca no ar em movimento descendente, sem realizar trabalho  —  sua trajetória é retilínea  —  como animal planador podemos citar o esquilo voador (Glaucomys volans)  —  possui geralmente uma pele que se

—  possui geralmente uma pele que se estende das patas dianteiras até as traseiras, denominada patágio.

 Vôos propulsionados  —  é o tipo de vôo realizado por grande parte dos animais que voam e é resultado da movimentação de músculos  —  devido a existência da força de arrastamento, um animal não consegue planar horizontalmente por muito tempo, devido a perda de velocidade  —  para voar horizontalmente com velocidade constante,uma força de impulso deve ser fornecida com direção igual, sentido contrário e mesma intensidade que a

força de arrastamento  —  essa potência é fornecida pelos músculos que impulsionam e movimentam as asas.

R- B.

 

Exercícios sobre conceitos das três leis de Newton

57- – Dados  —  m=1200kg  —  Vo=108/3,6=30m/s  —  V=0 (pára)  —  ∆S=200m  —  cálculo da aceleração de retardamento pela equação de Torricelli  —  V2 = Vo2 – 2.a.∆S  —  02 = 302 – 2.a.200  —  a=900/400=2.25m/s2  —  força resultante durante a frenagem  —  FR=m.a=1200.2,25  —  FR=2700N  —  essa força é a força de atrito que está segurando o carro  —  Fat=2700N  —  trabalho da força de atrito (realizado pelos freios)  —  WFat=Fat.d.cos180o=2700.200.(-1)  —  WFat= – 540000J=5,4.105 J  —  R- B.  

 58-  A intensidade da força resultante sobre os dois lutadores juntos, de massa M=200 + 200=400kg é de F_R=1000 – 950=950N  —  cálculo da aceleração   —  F_R=M.a  —  50=400.a  —  a=0,125m/s²  — 

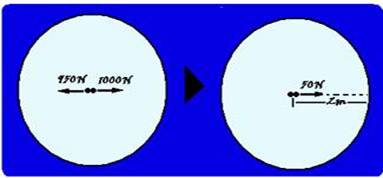
como eles se encontram no centro do círculo, para sair do mesmo eles devem percorrer R=∆S=2m  —  ∆S=V_ot + a.t²/2  —  2=0.t + 1,25.t²/2  —

t²=4/0,125  —  t=√32  —  t≈5,6s  —  R- E.

 

Tipos de força

39- Colocando as forças que agem sobre cada cinta, que correspondem ao acréscimo da força de contato entre a plataforma e o pneu, que no caso é a força (T) que traciona ou tensiona o fio em cada

      

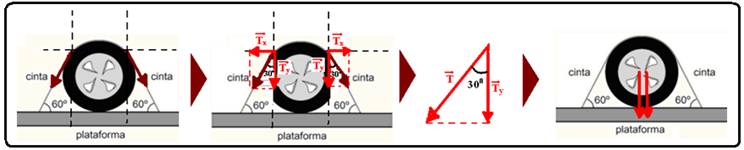
lado do pneu   —    decompondo essas forças na horizontal e na vertical (observe a seqüência da figura)  —  T_x=T.sen30^o=0,5.T  —  T_y=T.cos30^o=(√3/2).T  — observe que, na horizontal as componentes (T_x) se anulam  —  na vertical sobram, para baixo as duas forças T_y que pressionam a plataforma para baixo e que, somadas, fornecem  —  F = 2T_y=2x(√3/2)T   —  F =√3.T  —  R- D.     

40- O exercício quer o diagrama das forças que as dobradiças aplicam na porta:

Na horizontal: ao girar, a porta traciona  (puxa) para a direita a dobradiça superior e esta, pelo princípio da ação e reação reage na porta com uma força de mesma intensidade, mesma direção, mas sentido contrário, tracionando-a (puxando-a) para a esquerda com uma força   —  analogamente ao girar, a porta comprime  (empurra) para a esquerda a dobradiça superior e esta, pelo princípio da ação e reação reage na porta com uma força de mesma intensidade, mesma direção mas sentido contrário, comprimindo-a (empurrando-a) para a direita com uma força _. 

Na vertical, devido ao seu peso, a porta aplica em cada dobradiça uma força puxando-as para baixo e, elas reagem sobre a porta com forças  e , verticais e para cima.

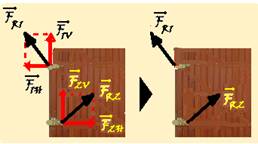
A soma vetorial dessas forças, fornece as forças resultantes  e que cada dobradiça exerce sobre a porta (figura)  R- D.

 

Peso e massa

33- O peso do corpo em Marte é o produto de sua massa que é a mesma em qualquer lugar ou planeta pela aceleração da gravidade na superfície do planeta Marte  —  P=m.g=3,10×3,69=11,439N  —  com três algarismos significativos  — 

P=11,4N  —  R- D.

34- Com duas pessoas no carro a deformação do sistema de molas é x=2cm=2.10^-2m e  a força que deformadora é o peso das duas pessoas  —  P=2mg=2.60.10=12.10²N  —  esse peso corresponde à força elástica  —  F_eP=kx  — 

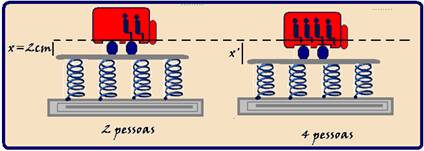
12.10²=k.2.10^-2  —  k=6.10⁴N/m (constante elástica do sistema de molas que é constante independente da força deformadora)  —  com  4 pessoas a deformação é x’ e o peso é P’=4mg=4.70.10=28.10²N  —   P’=kx’  —  28.10²=6.10⁴x’  —  x’=4,66.10^-2m=4,66cm  —  R- D.

 

Leis de Newton do MUV

48- a) Cálculo da aceleração do móvel no trecho AB  —  V_B = V_A + a.t  —  30 = 0 + a.10  —  a=3m/s²  —  como não

tem atrito a força resultante vale F_R=m.a=1200.3  —  F_R=3600N ou F_R=3,6.10³N.

b)  Parcela do peso na direção do movimento que diminui a velocidade do móvel durante a subida e que é a força resultante sobre ele  —  P_p=Psen30^o=m,g.sen30^o=1200.10.1/2  —  P_p=6000N  —  aceleração de subida  —  F_R=P_p=

m.a  —  6000=1200.a  —  a=5m/s² (retardamento)  —  ∆S=V_o.t + a.t²/2  —  o tempo de subida é t=(15 – 10)=5s  —

 ∆S=30.5 + (-5).5²/2  —   ∆S=87,5m.

No trecho BC a única força que age sobre ele, na direção do movimento é a parcela do peso (P_p=P.sen30^o) e, como não existe atrito, o sistema é conservativo  —  assim, a energia mecânica total do móvel em B (somente a cinética) é

igual à energia mecânica total do móvel em C  —  E_mC=E_mB= mV_B²/2=1200.30²/2  —  E_mC=540000J ou E_m

 

Plano inclinado sem atrito

25- Sendo o atrito com a plataforma da rampa desprezado a única força responsável pela descida das pessoas é a

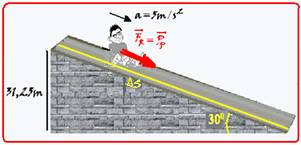
parcela do peso   paralela à superfície da plataforma, que é igual à força resultante  — P_p=Psen30^o=m.g.1/2=m.10/2  —  P_p=

5m (I)  —  F_R=m.a (II)  —  (I)=(II)  —  P_p=F_R  —  5m = ma  —  a=5m/s² (aceleração de descida das pessoas)  —  cálculo da distância percorrida ∆S pela rampa  —  sen30^o=31,25/∆S  —  0,5=31,25/∆S  —  ∆S=62,5m  —  ∆S=V_ot +

At²/2  —  pelo enunciado, partiu do repouso V_o=0  —  62,5=0.t + 5t²/2  —  t²=125/5  —  t=√25  —  t=5s  —  R- A.

26- Sendo o atrito desprezado, o sistema é conservativo  —  usando o teorema da conservação da energia mecânica  —  energia mecânica em P  — EmP = mVP2/2 + m.g.h = m.32/2 + m.10.0,8  —  EmP = 12,5m  —  Energia mecânica em Q  —  EmQ = mVQ2/2 + m.g.h = m.VQ2/2 + m.10.0  —  EmQ=mVQ2/2  —  EmP = EmQ  —  12,5m = mVQ2/2  —  VQ=√(25)  —  VQ=5,0 m/s.

27- I. Verdadeira  —  em (I) ela está em repouso, equilíbrio estático e F_R=0 o que implica que T=P=mg  —  em (II) ela

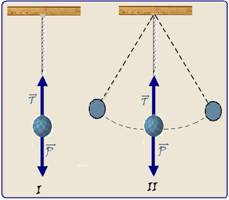
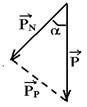
está em movimento circular surgindo sobre ela uma força resultante centrípeta (dirigida para o centro da circunferência) e de intensidade F_c=mV²/R, com F_c=T – P  —  T=P + mV²/R  —  observe, nesse caso, que T>P.

II. Verdadeira  —  As forças que agem sobre um corpo apoiado sobre um plano inclinado são seu peso, vertical e para baixo e a força normal , perpendicular à superfície de contato entre o bloco e o plano.

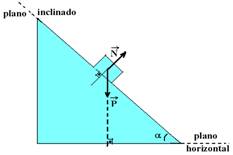
Α é o ângulo de inclinação do plano. Como  e  não tem a mesma direção, vamos decompor o peso  em duas parcelas:

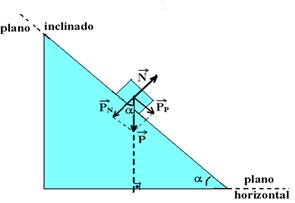
 parcela do peso paralela à superfície do plano inclinado (responsável pela tentativa de descida do bloco).

 parcela do peso perpendicular à superfície do plano inclinado (força que comprime o bloco contra o plano)

Observe que P_n é menor que o peso, pois é parcela do mesmo. 

III. Verdadeira  —  se a resistência do ar é nula, a aceleração de queda é a da gravidade g, que é constante, pois elas chegam juntas ao solo, quando largadas de mesma altura  —  P=mg  —  g=P/m=constante.

R- C.

 

Lei de Hooke

28- Com duas pessoas no carro a deformação do sistema de molas é x=2cm=2.10^-2m e  a força que deformadora é o peso das duas pessoas  —  P=2mg=2.60.10=12.10²N  —  esse peso corresponde à força elástica  —  F_eP=kx  — 

12.10²=k.2.10^-2  —  k=6.10⁴N/m (constante elástica do sistema de molas que é constante independente da força deformadora)  —  com  4 pessoas a deformação é x’ e o peso é P’=4mg=4.70.10=28.10²N  —   P’=kx’  —  28.10²=6.10⁴x’  —  x’=4,66.10^-2m=4,66cm  —  R- D.

29- Determinando  o valor da constante elástica k da mola pela figura 1  —  quando x=4,0cm=4.10^-2m, F=20N  —  F_e=kx  —  20=k.4.10^-2  —  k=5.10² N/m  —  força aplicada pela mola quando o sistema está em equilíbrio e a mola deformada de x=6,4cm=6,4.10^-2m  —  F=kx=5.10².6,4.10^-2=32N  —  observe a seqüência das figuras abaixo onde

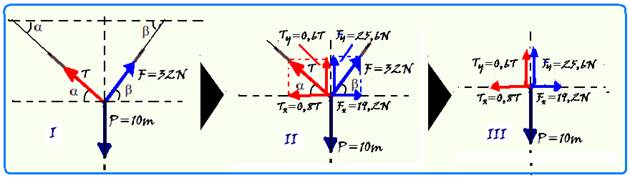
foram colocadas todas as forças no ponto de interseção dos fios (I)  —  em (II) foram decompostas as forças inclinadas  —  T_x=Tcosα=0,8T  —  T_y=Tsenα=0,6T  —  F_x=Fcosβ=32.0,6=19,2N  —  F_y=Fsenβ=32.0,8=25,6N  —  em (III) estão colocadas apenas as forças que agem nas direções horizontal e vertical  —  estando o sistema em equilíbrio essas forças se anulam em cada direção  —  na horizontal  —  0,8T=19,2  —  T=24N  —  na vertical  —  0,6T + 25,6 = 10m  — 

0,6.24 + 25,6 = 10m  —  14,4 + 25,6 = 10m  —  m=40/10=4kg  —  R- C.

 

Movimento Harmônico Simples (MHS)

Dinâmica do MHS – Sistema massa-mola

20- A. Falsa  —  F_e=kx  —  10=k.0,1  —  k=100n/m  —  k=10²N/m.

B. Falsa  —  o período de oscilação do sistema massa-mola vale  —  T=2π√(m/k)=2π√(0,25/10²)  —  T=2π√(25.10^-4)  —  T=2π.5.10^-2  —  T≈30.10^-2s.

C. Correta  —  a amplitude A vale A=20cm=2.10^-1m  —  energia mecânica nos extremos  —  E_me=k.A²/2=10².(2.10^–

¹)²/2  —  E_me=10².10^-2.4/2  —  E_me=2J  —  a velocidade é máxima no ponto médio onde a energia cinética é máxima  —  teorema da conservação da energia mecânica  —  E_me=E_c  —  2=m.V²/2  —  2=0,25.V²/2  —  V=16  —  V_max=4m/s.

D. Falsa  —  F=ma  —  F=kx  —  m.a=kx  —  0,25.a=10².2.10^-1  —  a=20/0,25  —  a=80m/s².

R- C.

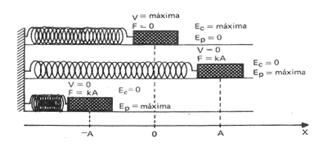
21- Na situação inicial (ponto I), de altura máxima, a força elástica vale F_e=3N  —  F_e=kx  —  3=100.x  —  x=0,03m   —  nesse ponto, a mola está comprimida de x=0,03m ao em relação à sua posição natural  —  na posição de equilíbrio (ponto O) a força resultante é nula e P_p=mgsen30^o=F_E=kd  —  1.10.1/2 = 100.d  —  d=0,05m  —  nesse ponto a mola está esticada de d=0,05m em relação à sua posição natural   —  sendo a amplitude A a distância entre a posição natural (ponto O) e a compressão máxima (pontoI), então A=0,03 + 0,05=0,08m  —  desprezados os atritos, a força elástica e a

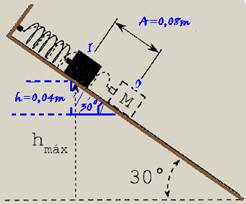
força peso são forças conservativas, então o sistema é conservativo e a energia mecânica do sistema é constante  —  colocando o nível de altura zero na posição de equilíbrio (ponto O) onde a mola está na posição natural (não deformada), a energia mecânica aí é só a cinética, pois a potencial gravitacional é nula (h’=0) e a potencial elástica também é nula (mola na posição natural, sem deformação)  —  E_mO=mv²/2  —  cálculo da altura no ponto I (veja figura)  —  sen30^o=h/0,08  —  0,5=h/0.08  —  h=0,04m  —  no ponto I a energia mecânica é a potencial elástica armazenada na mola (E_pe=kA²/2) somada com a potencial gravitacional (E_pg=mgh)  —  E_mI=kA^2/2 + mgh=100.(0,08)²/2

+ 1.10.0,04  —  E_pI= 0,32 + 0,4=0,36J  —  E_mI=E_mO  —  0,36=mv²/2  —  0,36=1.v²/2  —  V=√(0,64)  —  v=0,8m/s  —  R- B.

 

Função horária da elongação

15- O período de um sistema massa-mola efetuando um MHS é fornecido por T=2π√m/k  —  observe que se o sistema massa-mola estiver oscilando num plano inclinado, na horizontal ou na vertical, se a massa (m) do corpo e a constante elástica da mola (k) forem as mesmas, o que é o caso, o período de oscilação T será também o mesmo  —  R- D.

 

16- O período T desse MHS é fornecido pela expressão abaixo  —  substituindo m=0,08kg, k=0,5 N/m e  π = 3,14 na

 expressão T=2π√(m/k)  —  T=2.3,14.√0,08/0,5)=6,28.√(0,16)  —  T=6,28.0,4=2,512s  —  R- B.

 

Força de resistência no ar

36- a) São dados  —  V_o=6000m/s  —  V=0   —  t_o=0  —  t=7min=7.60=420s  —  cálculo da aceleração de

retardamento  —  a=(V – V_o)/(t – t_o)=(0 – 6000)/(420 – 0)  —  a=-14,3s  —  F_R=m.a=1000.(- 14,3)= – 14300N  —  em módulo  —

F_R=1,43.10⁴N.

b) Pelos dados ela entrou na atmosfera marciana com V_o=6000m/s em uma altitude de ho=125km=125.10³m e na altura

h=100km=100.10³m ela teve velocidade de V=4000m/s  —  Teorema da Energia Mecânica  —  Em todo sistema dissipativo, o trabalho das forças não conservativas (força de atrito, força de resistência do ar, etc.) é igual à  energia total dissipada, ou seja, é igual à variação da energia mecânica – E_mfinal – E_minicial=W_{forças dissipativas}  —  a força dissipativa

nesse caso é a força de atrito F_at  —  W_fat=E_m – E_mo  —  E_m=mV²/2 + mgh=10³.(4.10³)²/2 + 10³.10.100.10³=9.10⁹J  —

E_mo=mV_o²/2 + mgh_o=10³.(6.10³)²/2 + 10³.10.125.10³=19,25.10⁹J  —W_fat= – 10,25.10⁹  —  W_fat≈ – 1,0.10¹⁰J.

 

37- a) Pelo enunciado a intensidade da força vertical e para cima que o vento exerce sobre a gota vale F_vento=b.r com b=1,6.10^-3N/m  —  ρ_água=m/V  —  volume da gota considerada esférica de raio r  —  V=(4/3).π.r³  —  ρ_água=m/(4/3).π.r³  —  m=ρ_água.π.r³=10³.3.(4/3)r³  —  m=4.10³.r³  —  na iminência de começar a cair, o peso da gota

(vertical e para baixo) deve ser igual à força aplicada pelo vento (vertical e para cima)  —  P=F_vento  —  m.g = b.r  —  4.10³.r³.10 = 1,6.10^-3.r  —  r²= 1,6.10^-3/4.10⁴=0,4.10^-7  —  r=√(4.10^-8)  —  r=2.10^-4m=0,2mm  —  esse deve ser o raio da gota quando ela está na iminência de cair  —  para que ela caia você deve ter  —  r > 0,2mm.

b) Cálculo da massa dessa água que ocupa um volume V de água contida numa área de S=1m² e altura h=20mm=

20.10^-3m=2.10^-2m  —  V=S.h=1.2.10^-2=2.10^-2m³  —  ρ_água=m/V  —  10³=m/2.10^-2  —  m=20kg (é essa massa de água que ao se chocar com o solo provoca nele um impulso vertical e para baixo)  —  I=m.∆V  —  como o choque é inelástico, a variação de velocidade da água com o solo foi de ∆V=2,5m/s  —  I=20.2,5  —  I=50N.s,  impulso sobre o solo, vertical e para baixo.

 

Força de atrito

66- Força que ele aplica no pau de sebo comprimindo-o e trocando com ele uma força perpendicular ao poste de F=800N  —  pelo princípio da ação e reação o poste aplica nele uma força de mesma intensidade (N=800N), mesma direção mas sentido contrário  —  na vertical, existe sobre ele duas forças  —  seu peso vertical e para baixo e uma

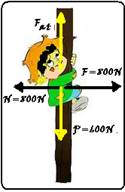
força de atrito, vertical e para cima que o impede de cair, anulando o peso  —  P=m.g=60.10  —  P=600N  —  N=800N  —F_at=μN=

μ.800  —  F_at=800μ  —  F_at=P  —  800μ=600  μ=600/800  —  μ=0,75  —  R- C.

67- Considerando os dois blocos como um único de massa M=(4 + 1)=5kg e sob ação da força de F=10N eles se movem com a mesma aceleração de F=Ma  —  10=5.a  —  a=2m/s² (aceleração de cada bloco)  —  sobre o bloco 2 agem as forças de intensidades F=10N (horizontal e para a direita) e a força de atrito F_at (horizontal e para a esquerda)  

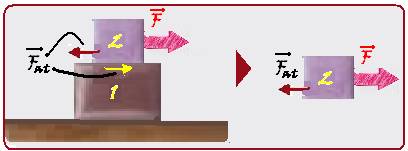
— força resultante sobre o bloco 2  —  F_R=F – F_at=10 – F_at  —  F_R=m₂.a  —  10 – F_at=1.2  —  F_at=8N  —  R- E.

68- Dados  —  m=0,4kg  —  t=0,8s  —  ∆S=1,6m  —  V_o=0  —  calculo da aceleração do garçom, copo e bandeja  —   ∆S=V_ot + at²/2  —  1,6=0.0,8 + a.(0,8)²/2  —  a=1,6/0,32  —  a=5m/s²  —  o copo de massa m=0,4kg que se move com a=5m/s² fica sob ação de uma força resultante  —  F_R=ma=0,4.5=2N  —  observe na figura abaixo onde foram colocadas

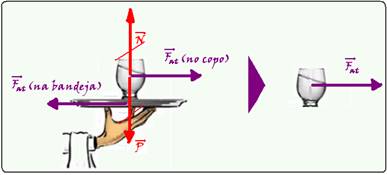
todas as forças que agem sobre o copo que essa força de 2N é a força de atrito que obriga o copo a acompanhar a bandeja e o garçom  —  FR=Fat=2N  —  R- A.

69- Dados  —  Vo=5m/s  —  V=0  —  ∆S=5m  —  cálculo da aceleração a do bloco utilizando a equação de Torricelli  —  V2 = Vo2 + 2.a. ∆S  —  02 = 52 + 2.a.5  —  a = – 2,5m/s2 (negativo, está retardando)  —  módulo da força resultante sobre o bloco de massa m  —  FR = m.a  —  FR=2,5m  —  mas, a única força sobre o bloco na direção do movimento é a força de atrito que o retém até parar  —  Fat=μ.N= μ.P= μ.mg=10μm  —  portanto, a força de atrito é a própria força resultante  —  Fat = FR  —  10μm = 2,5m  —  μ=0,25  —  R- E.

70- I. Comportamento das forças de atrito que agem em um carro sem o mecanismo ABS:

Considere um bloco de massa m sujeito a uma força externa de intensidade variável

Quando o corpo estiver em repouso e não houver força externa, F_at=0  —  com o corpo permanecendo em repouso, aumentando a intensidade de, a intensidade da força de atrito estático () também aumenta (figuras acima), até que o corpo fique na iminência de movimento (figura abaixo).

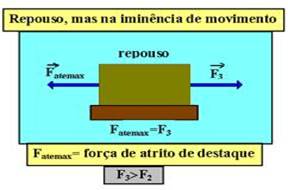
Quando o corpo está na iminência de movimento a intensidade da força de atrito estático é máxima  —  uma força de intensidade maior que  faz com que o corpo entre em movimento e, a partir daí a força de atrito é denominada dinâmica ou cinética.

Depois que o bloco entra em movimento a força de atrito é denominada força de atrito dinâmica, e é sempre a mesma,  independente da velocidade. A intensidade da força de atrito dinâmica é ligeiramente menor que a intensidade da força de atrito estática máxima.

O gráfico abaixo representa todo o processo explicado acima.

II. Comportamento das forças de atrito que agem em um carro com o mecanismo ABS:

Os freios antitravamento (ABS, anti-lock braking system) ajudam a parar melhor  —  eles previnem o

travamento das rodas e proporcionam uma distância de frenagem mais curta em superfícies escorregadias, evitando o descontrole do veículo  —  ele mantém as rodas sempre na iminência de deslizar, aproveitando melhor o atrito estático máximo, que é maior que o atrito cinético (de deslizamento)  —  quando a força aplicada pelos freios através da pressão aplicada no pedal chega aumentada até as rodas, estando elas na iminência de movimento (força de atrito de destaque), o sistema ABS libera instantaneamente a roda impedindo seu travamento e mantendo assim a força de atrito máxima (força de atrito de destaque) que é superior à força de atrito cinética ou dinâmica que surgiria, caso ele deslizasse  —  o

processo é repetido instantânea e sucessivamente conforme o gráfico acima  —  R- A.

 

Plano inclinado com atrito

32- Cálculo da intensidade da força de atrito estático (iminência de movimento)  —  F_ate=μ_e.N.cosθ= μ_e.P.cosθ=0,75.100.0,8  —  F_ate=60N  —  cálculo da intensidade da parcela do peso paralela ao plano inclinado que tende a puxar o bloco sobre o plano inclinado  —  P_p=Psenθ=100.0,6=60N  —  observe que a força resultante sobre o

bloco é nula e, como ele estava em repouso, por inércia ele tende a continuar em repouso, mas está na iminência de movimento)  —  R- E.

 

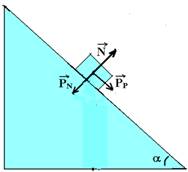
33- -As forças que agem sobre um corpo apoiado sobre um plano inclinado são seu peso, vertical e para baixo e a força normal , perpendicular à superfície de contato entre o bloco e o plano.

α é o ângulo de inclinação do plano. Como  e  não tem a mesma direção, vamos decompor o peso  em duas parcelas:

 parcela do peso paralela à superfície do plano inclinado (responsável pela tentativa de descida do bloco).

 parcela do peso perpendicular à superfície do plano inclinado (força que comprime o bloco contra o plano)

sena=cateto oposto/hipotenusa  —  sena=PP/P  —  PP=P.sena

cosa=cateto adjacente/hipotenusa  —  cosa=PN/P  —  PN=P.cosa (segunda figura acima)

A componente normal do peso  anula a reação normal do apoio , assim temos (terceira figura acima).

Havendo atrito:

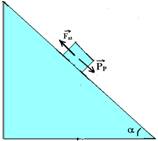
A força de atrito é sempre contrária ao movimento ou à sua tendência e é fornecida por F_at=mμN  —  P_N=N  —  F_at=mP_N  —  F_at=μPcosα  —  F_at=μmgcosα

Resolvendo o exercício  —  F_R=m.a  —  P_p – F_at =m.a  —  mgsenθ – μmgcosθ = ma  —  10.0,6 –

0,25.10.0,8 = a  — a=6 – 2  —  a=4,0m/s²  —  deslocamento ∆S entre A e B (veja figura abaixo)  — 

cosθ=cateto adjacente/hipotenusa  — 0,8 = BC/AB  —  0,8=2,4/∆S  —  ∆S=3m  —  para calcular a velocidade em B (V_B) você pode usar a equação de Torricelli  —  V_B² = V_A² + 2.a.∆S  —  V_B² = 1² + 2.4.3  —  V_B=5m/s  —  variação da quantidade de movimento entre A e B  —  ∆Q = Q_B – Q_A=mV_B – mV_A=50.5 – 50.1  —  ∆Q=200N.s  —  R- B.

 

Forças no movimento circular

49- Expressão da intensidade da força resultante centrípeta  —  F_c=mV²/R  —  kart  —  F_K=M.V²/2R=0,5MV²/R  —  fórmula 1  —  F_F=3M.V²/R=3MV²/R  —  stock-car  —  F_S=6M.V²/3R=2MV²/R  —  assim, F_F > F_S > F_K  —  R- B.

 50- Em todo movimento circular existe sempre uma força resultante dirigida para o centro da circunferência denominada força resultante centrípeta (

() de intensidade F_c=mV²/R  —  no ponto B essa força tem direção vertical e sentido para cima e de intensidade T – P =mV²/R  —  R- B.

 

Trabalho

48- Observe que durante todo os deslocamentos da moça num lugar plano, o ângulo que a força

peso dos brincos forma com o deslocamento (na nossa figura, horizontal) é sempre de 90^o  —  W_peso=P.d.cos90^o=p.d.0=0  —  R- E.

49- Como não existe atrito com o ar a intensidade da força resultante (F_R) sobre o conjunto (satélite-foguete) é igual à intensidade da força propulsora F_p) menos a intensidade da força peso (P)  —  intensidade da força peso  — 

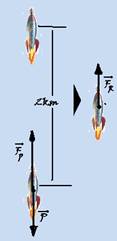
P=m.g=1.10⁶.10=10⁷N  —  F_R=F_p – P  —  F_R = 5.10⁷ – 1.10⁷=4.10⁷N  —  trabalho da força resultante  —   W_FR =

F­_R.d.cos0^o=4.10⁷.2.10³.1  —   W_FR=8.10¹⁰ J  —  R- D.

 

Potência

51- Dados  —  m=70kg  —  V_o=0  —  V=72km/h/3,6=20m/s  —  ∆t=2min=2.60=120s  —  cálculo do trabalho pela variação de energia cinética  —  W=E_c – E_co=mV²/2 – mV_o²/2=70.20²/2 – 70.0²/2  —  W=14000J  —  P=W/∆t  — P=14000/120  —  P=116,66W  —  R- A.

 

52- 01. Correta  —  pelo enunciado a massa total que sobe é a massa da gôndola (500kg) somada com sua carga (240kg)  —  peso   —  P=M.g=(500 + 240),g=740.10  —  P=7400N (peso de uma gôndola carregada)  —  a gôndola sobe com velocidade constante uma altura ∆S=100m em  ∆t=40s e sua velocidade média V_m será  —  V_m= ∆S/∆t=100/40  —  V_m=2,5m/s  —  a subida é um MRU, então a força resultante sobre a gôndola durante a subida é nula o que implica que

a intensidade da força média aplicada pelo motor equilibra a força peso  —  F_m=P=7400N  —  F_m=7400N  —  o trabalho da força média aplicada pelo motor na subida vale W=F_m.d,cos0^o=F_m.d.1  —  W=F_m.d  —  potencia média  — P_o=W/∆t   —  P_o=F_m.d//∆t  —  d//∆t=V_m  —  P_o=F_m,V_m=7400.2,5  —  P_o=18500W.

02. Correta  —  tempo que demora, em queda livre (a=g) para , a partir do repouso (V_o=0), atingir velocidade de V=122,4/3,6  —  V=122,4/3,6  =34m/s  —  V = V_o + g.t  —  34=0 + 10t  —  t=3,4s  —  cálculo da aceleração de retardamento a quando, descendo na vertical, com a velocidade passando de V_o=122,4/3,6=34m/s  até parar, quando V=0 em ∆t=8,4 – 3,4=5s  —  V=V_o – a.t  —  0 = 34 – a.5  —  a=34/5  —  a=6,8m/s²  —  força desaceleradora média  —  F­_R= m.a=740.6,8  —  F_R=5032N.

04. Falsa  —  é de 3,4s (veja 02).

08. Correta  —  a queda livre demorou t=3,4s, com a=g=10m/s² e V_o=0  —  ∆S=V_ot + at²/2=0.3,4 + 10.(3,4)²/2= 0 + 10.11,56/2=10.5,78  —  ∆S=57,8m.

16. Falsa  —  é g apenas na queda livre e não durante todo o percurso.

R- (01 + 02 + 08)=11.

 

Energia

26- Autocontração gravitacional (potencial gravitacional)  —  nesse processo, os íons de hidrogênio (prótons) contidos no seu interior adquirem  velocidades muito altas (energia cinética)  —  o que os leva a atingirem temperaturas da ordem de milhões de graus (energia térmica)  —  com isso, têm início reações exotérmicas de fusão nuclear, nas quais núcleos de hidrogênio são fundidos, gerando núcleos de He (Hélio) e propiciando a produção da radiação (energia de massa)  —  parte dessa radiação atinge a Terra (sob forma de radiação eletromagnética) e é a principal fonte de toda a energia que utilizamos  —  R- D.

 

27- a) Massa do atleta  —  m=70kg  —  como pedido no exercício, pelo gráfico 1, a terceira corrida demorou ∆t=t=0,5h num percurso de ∆S=7,5km  —  V=∆S/∆t=7,5/0,5  —  V=15km/h  —  pra essa velocidade V=15km/h, você verifica no gráfico 2 que C_MET=60kJ/kg.h  —  usando a expressão fornecida pelo enunciado do exercício  —  E=C_MET.m.t=60.70.

0,5  —  E=2100kJ.

b) Avaliando a área da sola de um tênis como um retângulo de 35cm=0,35m de comprimento e 9cm=0,09m de largura

 —  S=0,35×0,09=30,5.10^-4≈3.10^-5m²  —  pressão (P_r)=força(no caso, peso P)/área (S)  —  P=mg=70.10=700N  —  P_r=

P/S=700/3.10^-5  —  P_r≈2,3.10⁴ N/m² (Pa).

 

Tipos de energia – Trabalho

39-  Da mesma maneira que uma atiradeira (estilingue) transforma energia potencial elástica em energia cinética  devido à uma distensão da borracha (elástico) o carrinho mencionado também transforma energia potencial elástica em energia cinética devido à compressão da mola  —  R- E. 

 

Energia mecânica

72- Colocando o referencial na altura em que se encontra seu centro de massa, no início, quando ele finca a vara no chão para subir ele só possui energia cinética  —  E_c=mV²/2=m.11²/2  —  E_c=60,5m  — 

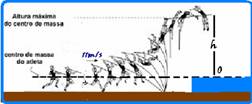
pelo enunciado, na altura Máxima, 80% de sua energia cinética é convertida em energia potencial gravitacional  —  E_pg=0,8xE_c=0,8×60,5m=48,4m  —  R_pg=m.g.h=48,4m  —  m.10.h=48,4m  —  h=4,84m  —  R- E.

73- a) As forças que agem sobre um corpo apoiado sobre um plano inclinado são seu peso, vertical e para baixo e a força normal , perpendicular à superfície de contato entre o bloco e o plano (figura abaixo).

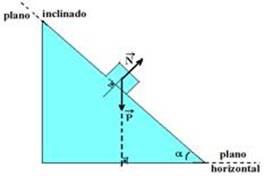
α é o ângulo de inclinação do plano. Como  e  não tem a mesma direção, vamos decompor o peso  em duas parcelas:

 parcela do peso paralela à superfície do plano inclinado (responsável pela tentativa de descida do bloco).

 parcela do peso perpendicular à superfície do plano inclinado (força que comprime o bloco contra o plano)

senα=cateto oposto/hipotenusa  —  senα=P_p/P  —  P_p=P.sena

cosα=cateto adjacente/hipotenusa  —  cosα=P_N/P  —  P_N=P.cosa

 

As duas forças acima substituem o peso e podemos tirá-lo:

A componente normal do peso  anula a reação normal do apoio , assim temos:

Como não existe atrito, o bloco desce com aceleração de intensidade a, tal que F_R=m.a  —   P_p=m.a  —  mgsenα=ma  —  a=gsenα.

Como o bloco está em equilíbrio na direção perpendicular à superfície do plano inclinado  —  N=P_N=Pcos30^o=10.√3/2  —  N≈5.1,7≈8,5N.

b) Veja em (a) que ele desce com aceleração a=gsen30⁰=10.1/2  —  a=5m/s²  —  aplicando Torricelli  —  V²=V_o² +

2.a.∆S  —  10²=0² + 2.5.d  —  d=100/10  —  d=10m.

c) Como não existe atrito o bloco 1 atinge o bloco 2 com velocidade de V₁=10m/s  —  antes do choque  —  V₁=10m/s  —  V₂=0  —  quantidade de movimento do sistema antes do choque  —  Q_sa=m₁V₁ + m₂V₂=1.10 + 3.0  —  Q_sa=10kg.

m/s  —   depois do choque  —  V’₁=?  —  V₂=4m/s  —  quantidade de movimento do sistema depois do choque  —  Q_sd=m₁V’₁ + m₂V₂=1.V₁’ + 3.4  —  Q_sd= V₁’ + 12  —  pelo princípio da conservação da quantidade de movimento  — 

Q_sa=Q_sd  —  10 = V₁’ + 12  —  V₁’= – 2m/s  (o sinal negativo significa que o bloco 1 retornou após o choque).

d) Cálculo da energia mecânica do bloco 2 no ponto A de altura zero e onde V=4m/s  —  E_mA=mV²/2 + mgh=3.4²/2 +

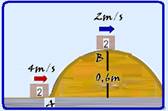
0  —  E_mA=24J  —  E_mB=mV_B²2 + m.g.R=3.V_B²/2 + 3.10.0,6  —  V_B=√4=2m/s  —  no ponto mais alto B, a força resultante sobre o bloco é a centrípeta, vertical e dirigida para o centro da circunferência (baixo), de intensidade  —

F_c=mV_B²/R  —  P – N = 3.2²/0,6  —  30 – N = 20  —  N=10N.

74- Utilizando o teorema da conservação da quantidade de movimento do sistema  —  antes do disparo —  Q_antes=(M + m)V=(M + m).0  —  Q_antes=0  —  depois do disparo  —  o canhão de massa M se move para a direita com velocidade

V e o projétil de massa m para a  com velocidade ( – v)  —  Q_depois =MV – mv  —  Q_antes = Q_depois  —  0 = MV –mv  —

V=mv/M  —   após o disparo o canhão de massa M se desloca para a direita com velocidade inicial V_i=mv/M até parar V_f=0, percorrendo uma distância d  —  a energia dissipada pela variação de energia cinética (∆E_c) do canhão é igual à

energia dissipada pela força de atrito (W_fat)  —   ∆E_c = W_fat  —  MV_f²/2 – MV_i²2 = F_at.d.cos180^o  —   M.0²/2 – M(mv/M)²/2 = F_at.d.(-1)  —   0 – M.(m²v²/M²)/2 = – μNd  —  N=P=Mg  —  M.m².v²/2M² = μMgd  —  μMgd = m²v² /2M  —  μ = m²v²/2M²gd  —  μ = (mv/M)²/2gd  — R- A.

75- A energia mecânica antes do disparo que vale Ema=3,75J e é a soma das energia cinética Ec=mV2/2 com a potencial elástica armazenada na mola (Epel)  —  Ema = Ec + Epel  —  3,75=mV2/2 + Epel  —  3,75 = (3 + 3).12/2 + Epel  —  Epel=0,75J  —  agora você deve utilizar o teorema da conservação da quantidade de movimento  —  antes do disparo do gatilho  —  Qsa=mA.VA + mB.VB=3.1 + 3.1=3kgm/s  —  depois do disparo do gatilho  —  Qsd=mAVA + mBVB=3VA + 3.1,5=3VA + 4,5  —  Qsa = Qsd  —  3=3VA + 4,5  —  VA=1,5/3=0,5m/s.

76- a) Dados  —  m_m=10¹⁶kg  —  V_m=30km/s=30.10³=3.10⁴m/s  —  quantidade de movimento inicial do meteoro  —  P_i=m_m.V_m=10¹⁶.3.10⁴=3.10²⁰ kg.m/s

b) Definição de energia cinética  —  E_ci = m_m.V_m²/2=10¹⁶.(3.10⁴)²/2  —  E_ci=10¹⁶.9.10⁸/2  —  E_ci=4,5.10²⁴ J.

c) Utilizando o princípio da conservação da quantidade de movimento do sistema (Terra-meteoro) antes e depois do fenômeno (colisão)  — antes da colisão  —   P_i = P_mi + P_Ti=m_m.V_m + m_T.V_T  —  mas, V_T=0 (antes da colisão, a Terra não se move na direção perpendicular à sua trajetória, veja figura)  —  P_i=10¹⁶.3.10⁴ + 6.10²⁴.0  —  P_i=3.10²⁰ + 0  — 

—  P_i=3.10²⁰kg.m/s  —  depois da colisão  —  trata-se de uma colisão inelástica (Terra e meteoro se movem juntos, com a mesma velocidade V)  — P_f = P_mf + P_Tf=m_m.V + m_T.V=(m_m + m_T),V  —  como a massa do meteoro é insignificante em relação à massa da Terra, você pode considerar (m_m + m_T)≈m_T  —  P_f=m_T.V=6.10²⁴V  —  pelo princípio da conservação da quantidade de movimento  —  P_i = P_f  —  3.10²⁰=6.10²⁴V  —  V=3.10²⁰/6.10²⁴  — 

V=5,0.10^-5 m/s (velocidade ‘Terra + meteoro” , no nosso exemplo para a direita, imediatamente após a colisão).

c) Cálculo da energia cinética final do sistema (Terra + meteoro)  —  E_cf=m_{(m + T)}.V²/2=m_T.V²/2=6.10²⁴.(5.10^-5)²/2  — 

E_cf=7,5.10¹⁵J  —  essa energia cinética final do sistema (7,5.10¹⁵J) é muito menor do que a energia cinética inicial do meteoro (4,5.10²⁴J)  —  assim, a energia dissipada no choque é praticamente igual à energia cinética inicial do meteoro  —  E_d=4,5.10²⁴J  —  regra de três  —  1 megaton – 4.10¹⁵J  —  E_d – 4,4.10²⁴J  —  E_d=4,4.10²⁴/4.10¹⁵  — 

E_d=1,125.10⁹ megatons.

 

Impulso e quantidade de movimento

39- Utilizando o teorema da conservação da quantidade de movimento do sistema  —  antes do disparo —  Q_antes=(M + m)V=(M + m).0  —  Q_antes=0  —  depois do disparo  —  o canhão de massa M se move para a direita com velocidade

V e o projétil de massa m para a  com velocidade ( – v)  —  Q_depois =MV – mv  —  Q_antes = Q_depois  —  0 = MV –mv  —

V=mv/M  —   após o disparo o canhão de massa M se desloca para a direita com velocidade inicial V_i=mv/M até parar V_f=0, percorrendo uma distância d  —  a energia dissipada pela variação de energia cinética (∆E_c) do canhão é igual à

energia dissipada pela força de atrito (W_fat)  —   ∆E_c = W_fat  —  MV_f²/2 – MV_i²2 = F_at.d.cos180^o  —   M.0²/2 – M(mv/M)²/2 = F_at.d.(-1)  —   0 – M.(m²v²/M²)/2 = – μNd  —  N=P=Mg  —  M.m².v²/2M² = μMgd  —  μMgd = m²v² /2M  —  μ = m²v²/2M²gd  —  μ = (mv/M)²/2gd  — R- A.

40- Teorema do Impulso: “ O impulso da força resultante de um sistema de forças que age sobre um corpo é igual à variação da quantidade de movimento do corpo”

 Se uma bola de massa m incide perpendicularmente numa parede com velocidade de módulo V e retorna na mesma direção, mas em sentido contrário com velocidade de mesmo módulo, teremos:

F.∆t = m.V_f – m.V_i  —  F.∆t = m.(+V) – m.(-V)  —  F ∆t = m.V – (- m.V)  —  F.∆t = mV + mV  —  F ∆t = 2mV    

No caso do exercício  —  V_antes=V_a=-40m/s  —  V_depois=V_d=+30m/s  —  F.∆t = m.V_d – m.V_a  —  F.∆t = m.(+30) – m.(-

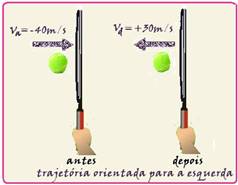
40)  —  F.∆t = 30m + 40m  —  F.10^-2=70×6.10^-2  —  F=420,10^-2/10^-2  —  F=420N  —  R-D.

41- Teorema do Impulso:“ O impulso da força resultante de um sistema de forças que age sobre um corpo é igual à variação da quantidade de movimento do corpo”

Muitos automóveis dispõe de um eficiente sistema  de proteção para o motorista, que consiste de uma bolsa inflável de ar (air-bag)  —  essa bolsa é automaticamente inflada quando o automóvel sofre uma desaceleração súbita, de modo que a cabeça e o tórax do motorista, em vez de colidirem com o volante, colidem com a bolsa.

Veja pela expressão F.∆t=m.∆V, que m e ∆V são constantes (mesmo motorista e mesma variação de velocidade) e assim, teremos  —  F. ∆t=constante, portanto se você aumentar o intervalo de tempo do choque, estará diminuindo a intensidade da força máxima que o motorista troca com o volante.

Assim, a bolsa aumenta o intervalo de tempo da desaceleração da cabeça do motorista, diminuindo, portanto, a força máxima que atua sobre a cabeça e o tórax  —  R- A.

42- Como o sistema é isolado, a quantidade de movimento do sistema antes da colisão () deve ser igual à quantidade de movimento do sistema depois da colisão ()  —  a quantidade de movimento

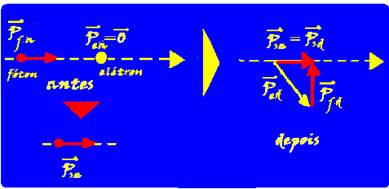
do sistema antes da colisão tem direção horizontal e sentido para a direita, sendo a do próprio fóton, pois a do elétron é nula (figura)  —  a quantidade de movimento do sistema depois da colisão também deve ter direção horizontal e sentido para a direita, pois =  —  então a soma vetorial de com  deve fornecer = (veja figura)  —  R- A.

43- A energia mecânica antes do disparo que vale Ema=3,75J e é a soma das energia cinética Ec=mV2/2 com a potencial elástica armazenada na mola (Epel)  —  Ema = Ec + Epel  —  3,75=mV2/2 + Epel  —  3,75 = (3 + 3).12/2 + Epel  —  Epel=0,75J  —  agora você deve utilizar o teorema da conservação da quantidade de movimento  —  antes do disparo do gatilho  —  Qsa=mA.VA + mB.VB=3.1 + 3.1=3kgm/s  —  depois do disparo do gatilho  —  Qsd=mAVA + mBVB=3VA + 3.1,5=3VA + 4,5  —  Qsa = Qsd  —  3=3VA + 4,5  —  VA=1,5/3=0,5m/s.

 

Colisões mecânicas

49- 01- a) Falsa  —  quantidade de movimento (Q)=massa (m)xvelocidade (V)  —  bola de vôlei  —  Q_V=m_V.V_V=(0,27).(30)  —  Q_V=8,1kg.m/s  —  bola de golfe  —  Q_G=m_G.V_G=(0,045).(60)  —  Q_G=2,7kg.m/s  — 

Q_G < Q_V.

b) Falsa  —  E_c=m.V²/2  —  bola de vôlei  — E_cV=m_V.V_V²/2=(0,27).(30)²2  —  E_cV=121,5J  —  bola de golfe  —  E_cG=m_G.V_G²/2=(0,045).(60)²/2  —  E_cG=81J  —  E_cG < E_cV.

c) Falsa  —  em todo choque inelástico o coeficiente de restituição é nulo o que implica que, os corpos após o choque, possuem a mesma velocidade e, como a massa da pessoa é bem maior que a das bolas, cada uma delas terá velocidade final nula   — V_fV=0  e V_fG=0.

d) Falsa  —  “O impulso da força resultante de um sistema de forças que age sobre um corpo é igual à variação da quantidade de movimento do corpo”

∆t_V= 2∆t_G  —  m_V=0,27kg  —  m_G=0,045kg  —  V_G=60m/s  —  V_V=30m/s  —  F_G. ∆t_G=0,045×60=2,7 (I)  —  F_V.2∆t_G=0,27×30=8,1 (II)  —  (I)/(II)  —  F_G.∆t_G/2F_V.∆t_G=2,7/8,1  —  F_G/2F_V=1/3  —  F_G=2F_V/3  —  F_G < F_V.

e) Correta  —  Pressão=força/área  —  P=F/S  —  P_G=F_G/S_G=2F_V/3 (I)  —  S_V=10S_G  —  P_V=F_V/S_V=F_V/10S_G (II)  —

(I)/(II)  —  P_G/P_V=2F_V/3S_Gx10S_G/F_V  —  P_G/P_V=(20/3)P_V  —  P_G > P_V.

R- E.

 50- Sendo a colisão perfeitamente elástica, a energia mecânica (no caso, cinética) do sistema, antes

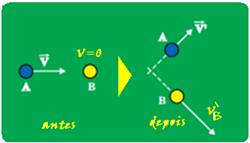
e depois da colisão é a mesma  —  antes  —  E_ca=m.2²/2 + m.0²/2  —  E_ca=2m  —  depois  —  E_cd=mV’²/2 + mV_B’²/2=m.1²/2 + mV_B’²/2  —  E_cd=0,5m + mV_B’²/2  —  E_ca = E_cd  —  2m = 0,5m + mV_B’²/2  —  V_B’²=3   —  razão pedida  —  E_B^’=mV_B’²/2=m.3/2 (I)  —  E_A=m.4/2=2m (II)  —  (I)/(II)  —  E’_B/E_A = (3m/2)/2m=(3m/2)x(1/2m)  —  E’_B/E_A=3/4  —  R- C.

 51- Após o primeiro choque  —  h₁=0,8×5=4,0m  —  após 0 segundo choque  —  h₂=0,8×4,0=3,2m  —  após o terceiro choque  —  h₃=0,8×3,2=2,56m  —  R- C.

52- No primeiro choque ela chega ao solo com  —  E_mi=mgh=E_mf=mV²/2  —  m.10.5=mV²/2  —  v=10m/s  —  80%de 10m/s=8m/s  —  aos o primeiro choque ela se solta do solo com  —   E_mi=mV²/2=E_mf=mgh=m.10.4  —  V=√80=8,9ms  —  R- D.

53- Intensidade da força sobre a bola 1  —  F₁=3m₂.a₁=3m₂.3=9m₂  —  intensidade da força sobre a bola 2  —  F₂=m₂.a₂  —  mas, pelo princípio da ação e reação essas forças tem a mesma intensidade  —  F₁=F₂  —  9m₂=m₂.a₂==   a₂=9m/s²

R- B.

 

Voltar para os exercícios