Reflexão da Luz – Espelhos Planos – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Reflexão da Luz – Espelhos Planos
01- Veja esboço abaixo
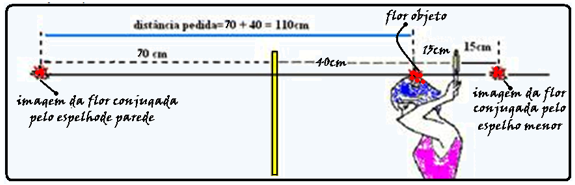
R-D.
02- O caminhão X se aproxima do carro com velocidade relativa de VXo=50 – 40 =10km/h e a jovem vê, pelo espelho retrovisor, sua imagem se aproximar com o dobro desse valor, ou seja, VXi=20km/h.

Então o caminhão Y, para manter velocidade relativa de 10km/h deve se mover para a direita com velocidade de VYo=30 – 20=10kmh — R- E.
03- Objeto e imagem são equidistantes do espelho (veja esquema abaixo).
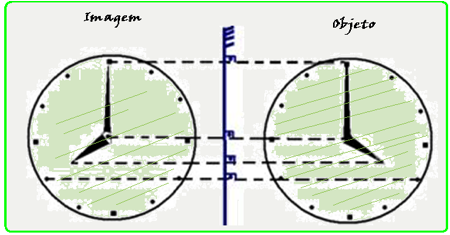
R- D.
04- Os raios de luz para serem vistos pelo observador P devem sair do objeto, sofrer reflexão no espelho e atingir os olhos do observador P, mas o prolongamentodesses raios deve chegar até a imagem do observador que é P’ — o raio incidente A é interrompido no anteparo e não é visto — os raios B e C incidem no espelho e se refletem atingindo os olhos do observador P, que os vê — o raio refletido D é interrompido no anteparo não atingindo os olhos do observador que não o vê — o raio E não atinge o espelho não sofrendo, portanto, reflexão e não atingindo o observador –— R- D.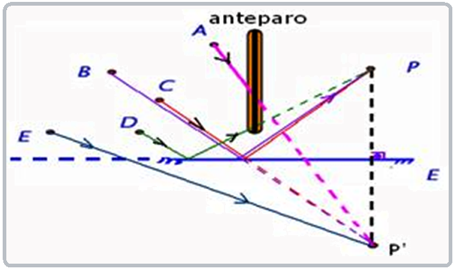
05-
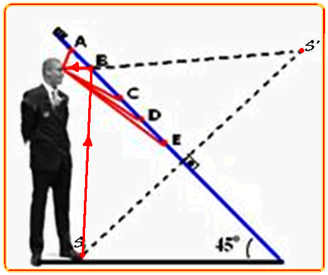
Localizar (s’), imagem de (s), equidistantes do espelho— o raio de luz sai do ponto S do sapato, atinge o espelho em B, sofre reflexão aí e atinge o olho da pessoa, fazendo-a enxergar S — R- B.
06- Quando o raio de luz incide em cada espelho você traça a normal em cada ponto de incidência e o ângulo de incidência e o de reflexão em cada caso são iguais (espelho de cima 10o e o de baixo 20o)— observe no triângulo
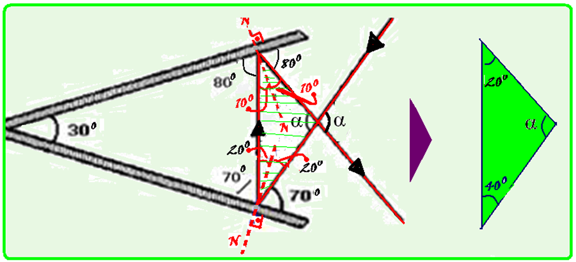
hachurado que a soma dos ângulos internos é de 180o,ou seja, α + 20 + 40=180 — α=120o— R- D.
07– Veja a figura abaixo onde se pede para determinar a distância d— aplicando Pitágoras no triângulo hachurado —
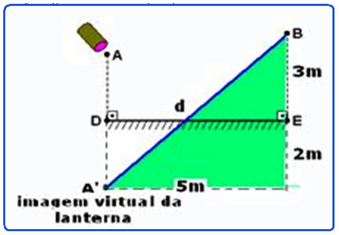
triângulo hachurado — d2 = 52 + 52=2.52 — d=5√2 m
08- A partir dos comprimentos indicados, pode-sedesenhar um triângulo retângulo em que a hipotenusa é a distância
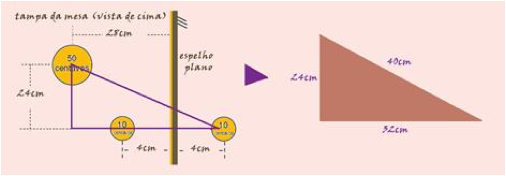
da moeda de 50centavos à imagem da moeda de 10 centavos e os catetos valem 24 cm e (28 cm + 4 cm)= 32 cm, onde o segmento de tamanho 4 cm se originou da distância da imagem da moeda de 10 centavos ao espelho — teorema de Pitágoras, a hipotenusa desse triângulo retângulo é igual a 40 cm — R- D.
09- A expressão (n=360/α – 1) só é válida para um objeto — n=360/60 – 1 — n=5 imagens de um indivíduo— 2 indivíduos – 10 imagens + os 2 objetos — na foto aparecem 12 indivíduos.
10- Sendo α=90o— n=360/α – 1 — n=360/90 – 1=4 – 1=3 imagens — aimagem frontal aos dois espelhos está de
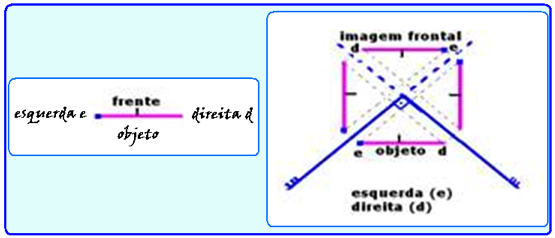
frente para o objeto e objeto e imagem frontal não são reversos ou revertidos, ou seja, não trocam direita pela esquerda
R- A
11-Observe as figuras abaixo onde a primeira imagem P’ (conjugada pelo espelho E) funciona como objeto para o espelho E’, originando a imagem P’’, que é vista pelo observador (figura da esquerda) e
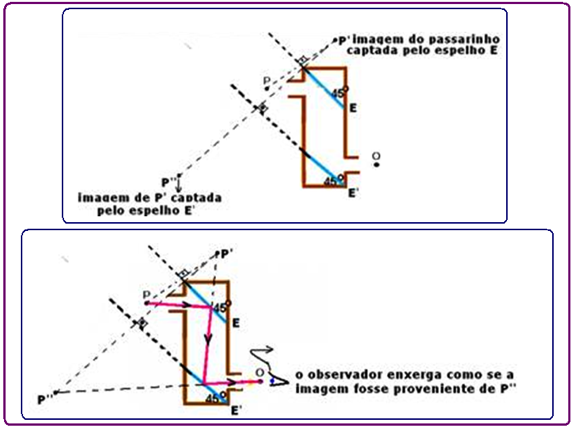
os raios de luz que possibilitam essa visualização estão na figura da direita. Esses dois espelhos planos que constituem o periscópio fornecem, a partir da luz proveniente de um objeto real (no caso, o passarinho), uma imagem final P’’ virtual, do mesmo tamanho do objeto e não reversa (não troca direita pela esquerda).
12– a), b) e c)
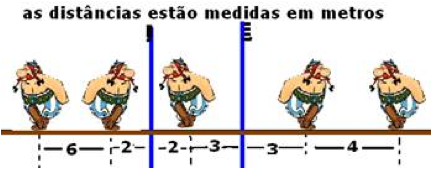
13- Como a imagem da foto do quadro é invertida e reversa, o quadro original Q, que é o objeto, terá a aparência da figura 1 — O sistema de espelhos deixa a imagem desse objeto, invertendo-o e
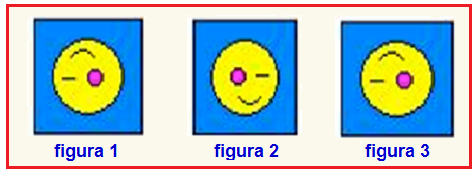
revertendo-o conforme a figura 2 — a máquina fotográfica capta a imagem anterior, invertendo-a e revertendo-a novamente e deixando-a como na figura 3.
R- A
14- Observe que α = 4 n — o número de imagens (n) obtidas pela associação de dois espelhos planos que formam entre si um ângulo α (em graus) é dado pela expressão — n=(360/ α) – 1 — n=(360/4n) – 1 — n2 + n -90=0 — n=-1 ± √(12 + 360)/2 — n= (- 1 ± 19)/2 — desprezando a resposta negativa — n=9 — α=4n — α=36o
